задачи. Сборник задач на построение сечений призмы Составила учитель математики и информатики мбоу Школа 6
 Скачать 0.73 Mb. Скачать 0.73 Mb.
|
|
Муниципальное бюджетное общеобразовательное учреждение «Школа № 6» город Прокопьевск Кемеровская область» Сборник задач на построение сечений призмы Составила учитель математики и информатики МБОУ «Школа № 6» Игнашева Оксана Павловна 2019 Треугольная призма №1. В правильной треугольной призме ABCA1B1C1 стороны основания равны 6, боковые рёбра равны 4. Изобразите сечение, проходящее через вершины A, B и середину ребра A1C1 Найдите его площадь. П 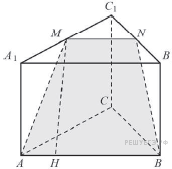 остроение: остроение: 1) Обозначим через M и N средины ребер A1C1 и B1C1 соответственно. 2) По Теореме о средней линии треугольника MN ׀׀ A1B1 ׀׀ AB, так что прямые MN и AB лежат в одной плоскости. 3) Искомое сечение — это равнобедренная трапеция AMNB. Решение: Основания трапеции Проведем в трапеции высоту Отрезок Следовательно, высота трапеции 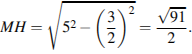 Зная её, находим площадь трапеции: 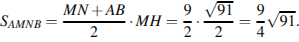 Ответ: №2. Построить сечение правильной треугольной призмы ABCA1B1C1 плоскостью, проходящей через середины ребер AB, A1C1, BB1. Найти площадь сечения и вычислить угол между плоскостью основания ABC и плоскостью сечения, если сторона основания равна 4, а высота пирамиды равна 42−√/7. П 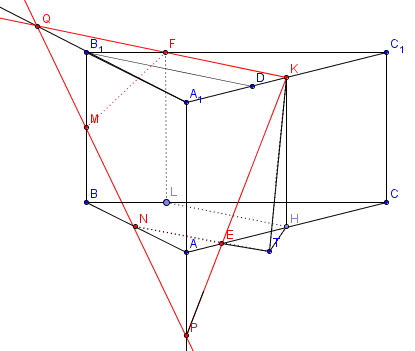 остроение: остроение: 1)MN∩AA1=P, 2)MN∩B1A1=Q, 3)PK∩AC=E, 4)QK∩B1C1=F 5)Пятиугольник MNEKF искомое сечение. Построение: 1) Обозначим AB=a,BB1=b,∠NEA=α ΔAPN=ΔBMN=ΔB1MQ⇒AP=MB=b2,A1P=3b2,QB1=a2 ΔAPE∼ΔA1PK⇒AE=13A1K=a6. 2)Из треугольника ANE, по теореме косинусов и синусов NE=AN2+AE2−2AN⋅AEcos60√=a7√6,sinα=33√27√. 3)Пусть KH⊥AC,HT⊥NE. По теореме 3-х перпендикуляров KT⊥NE. Угол наклона сечения будет ∠KTH. EH=AH−AE=A1K−AE=a2−a6=a3,TH=BB1=b. 4) Из треугольника THE,HT=EHsinα=a3⋅33√27√=a3√27√, а из треугольника KHT,KT=KH2+HT2,√=b2+3a228, √=28b2+3a228, √,cos∠KTH=THKT= =a3√28b2+3a2√=6√3⇒∠KTH=arccos23√=arcsin13. 5)Если проводить B1D||QK, то по обобщенной теореме Фалеса легко доказать, что C1F=34a. 6)Проекция сечения на основание будет BLHEN. SBLHEN=SABC−SANE−SCHL=a23√4−12⋅a2⋅a6⋅3√2−12⋅a2⋅3a4⋅3√2= =133√a296=133√6 Sсеч.=Sпр.cos∠KTH=133√6⋅3√2√=132√4. Ответ:132√4. №3. В правильной треугольной призме ABCA1B1C1 со стороной основания а и высотой H=na . Найти площадь сечения призмы плоскостью, проходящей через вершину C и середины ребер AA1 и A1B1. Построение: 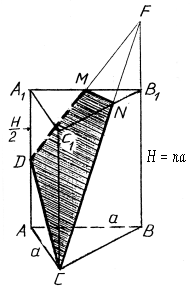 1)Так как A1DM = B1FM, то B1F = 1)Так как A1DM = B1FM, то B1F = 2)Отрезок MN находим из MNB1 по теореме косинусов; диагональ CM можно найти из прямоугольного треугольника CC1M (на рисунке не показан). 3)Площадь четырехугольника CDMN определяем по сумме площадей треугольников CDM и CMN, введя вспомогательные углы и . 4)SCDM = 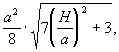 SCMN = SCMN = 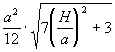 ; ;Sсеч. = 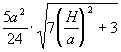 . .Возможные варианты: n = n = №  4.Построить сечение правильной треугольной призмы ABCA1B1C1 плоскостью, проходящей через прямую CM и параллельной диагонали AC1 боковой грани ACC1A1, если точка M – середина ребра B1C1. 4.Построить сечение правильной треугольной призмы ABCA1B1C1 плоскостью, проходящей через прямую CM и параллельной диагонали AC1 боковой грани ACC1A1, если точка M – середина ребра B1C1.Построение: 1) В плоскости ACC1 проводим прямую CK || AC1 (точка K - пересечение прямой CK с плоскостью A1B1C1)- тогда плоскость проходящая через прямые CM и CK будет параллельна прямой AC1; 2) в плоскости A1B1C1 проводим прямую KM - до ее пересечения с ребром A1B1 в точке D; 3) и "если 2 параллельные плоскости пересекает 3-я плоскость, то линии пересечения параллельны", т.е. в плоскости ABC проводим CE || MD. Трапеция CMDE - искомое сечение. №5. 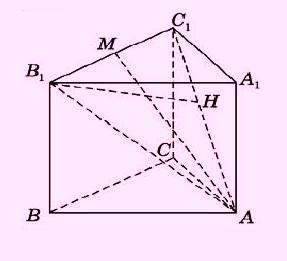 Построить сечение треугольной призмы проходящее через точки A, B и H, лежащую на стороне AC1. Построить сечение треугольной призмы проходящее через точки A, B и H, лежащую на стороне AC1.Построение: 1) проведём C1A и отметим на ней произвольную точку H 2) соединим точку B и точку A (т.к. они лежат в одной плоскости ABB1A1 ) 3) соединим точку B1 и точку C1 4) соединим точку A и точку C1 ( т.к.они лежат в одной плоскости AA1C1C ) 5) соединим точки A, B1 и C1 и получим плоскость AB1C1 6) соединим точку B и точку H ( т.к. они лежат в одной плоскости AB1C1 ) 7)B1HA - искомое сечение. Задачи для самостоятельного решения: №1. Постройте сечение призмы АВСА'В'С' плоскостью, проходящей через точку D, лежащую на ребре AC, точку E на ребре ВВ' и точку F на ребре В′C′. №2. В правильной треугольной призме АВСDEF AB = AD, N – середина EF. Постройте перпендикулярное сечение призмы плоскостью, проходящей через точку М на ребре АВ перпендикулярно AN. №3. Постройте сечение призмы АВСА'В'С' плоскостью, проходящей через точку D, лежащую в грани AA′C′C, точку E в грани AА'В'B и точку F в грани ВВ′C′C. №4. Найдите площадь сечения правильной треугольной призмы ABCA1B1C1 плоскостью, проходящей через прямую CM и параллельной диагонали AC1 боковой грани ACC1A1, если точка M – середина ребра B1C1, сторона основания равна sqrt(14), а боковое ребро равно sqrt(3). №5. В правильной треугольной призме ABCA1B1C1 стороны основания равны 8, боковые рёбра равны √13. Изобразите сечение, проходящее через вершины A,C и середину ребра A1B1. Найдите его площадь. Четырёхугольная призма № 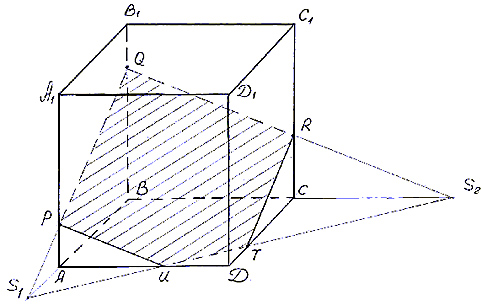 1. Построить сечение призмы ABCDA1B1C1D1 плоскостью, проходящей через точки P, Q, R. 1. Построить сечение призмы ABCDA1B1C1D1 плоскостью, проходящей через точки P, Q, R. Построение: 1) Построим след секущей плоскости на плоскость нижнего основания призмы. Рассмотрим грань АА1В1В. В этой грани лежат точки сечения P и Q. Проведем прямую PQ. 2) Продолжим прямую PQ, которая принадлежит сечению, до пересечения с прямой АВ. Получим точку S1, принадлежащую следу. 3)Аналогично получаем точку S2 пересечением прямых QR и BC. 4) Прямая S1S2 - след секущей плоскости на плоскость нижнего основания призмы. 5) Прямая S1S2 пересекает сторону AD в точке U, сторону CD в точке Т. Соединим точки P и U, так как они лежат в одной плоскости грани АА1D1D. Аналогично получаем TU и RT. 6) PQRTU – искомое сечение. №2. Построить сечение куба плоскостью, проходящей через точки: П 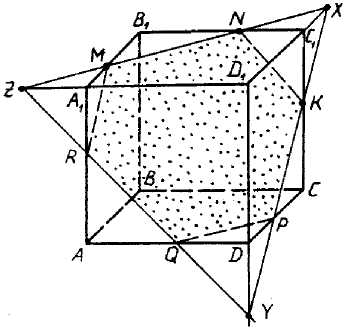 остроение: остроение: Точки MиN принадлежат плоскости А1В1С1. Соединив их, получим линию пересечения секущей плоскости и плоскости верхней грани куба (нажимаем клавишу мыши). Продолжим прямые MN и D1C1до пересечения. Получим точку Х, принадлежащую как плоскости А1В1С1 , так и плоскостиDD1C1 (клик мыши). 2) Точки Nи К принадлежат плоскостиВВ1С1. Соединив их, получим линию пересечения секущей плоскости и грани ВВ1С1С. (Клик мыши). 3) Соединяем точки Х и К,и продолжаем прямую ХКдо пересечения с прямой DC. Получим точку Р и отрезок КР –линию пересечения секущей плоскости и грани DD1C1C. Продолжая прямые КРи DD1 до пересечения, получим точку Y, принадлежащую плоскости АА1D1. В плоскости этой грани нам требуется еще одна точка, которую получаем в результате пересечения прямых MNи А1D1. Это точка Построение (краткая запись): 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 13) № 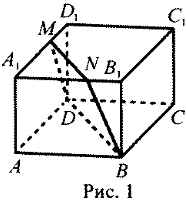 3. 3.. В правильной четырёхугольной призме Построение: Отрезок Треугольники Значит, 3)В равных прямоугольных треугольниках значит, трапеция 4)Пусть Ответ: 144√2 №4. В правильной четырёхугольной призме Построение: 1 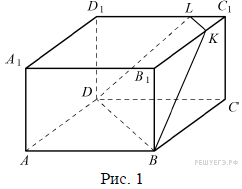 )Пусть )Пусть 2)Так как плоскости 3)Искомое сечение — трапеция 4) Плоскость сечения пересекает нижнее основание по прямой 5)Треугольники LC1K и D1C1B1 подобны, следовательно, Значит, 6)В равных прямоугольных треугольниках Пусть Ответ: №5. Построить сечение прямой призмы ABCDA1B1C1D1 плоскостью, проходящей через точки M, N, P . Построение: 1 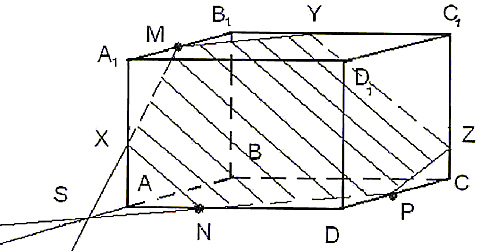 ) Точки N и P лежат в плоскости сечения и в плоскости нижнего основания параллелепипеда. Построим прямую, проходящую через эти точки. Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда. ) Точки N и P лежат в плоскости сечения и в плоскости нижнего основания параллелепипеда. Построим прямую, проходящую через эти точки. Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда.2) Продолжим прямую, на которой лежит сторона AB параллелепипеда. Прямые AB и NP пересекутся в некоторой точке S. Эта точка принадлежит плоскости сечения. 3) Так как точка M также принадлежит плоскости сечения и пересекает прямую АА1 в некоторой точке Х. 4) Точки X и N лежат в одной плоскости грани АА1D1D, соединим их и получим прямую XN. 5) Так как плоскости граней параллелепипеда параллельны, то через точку M можно провести прямую в грани A1B1C1D1, параллельную прямой NP. Эта прямая пересечет сторону В1С1 в точке Y. 6) Аналогично проводим прямую YZ, параллельно прямой XN. Соединяем Z с P. Искомое сечение – MYZPNX. Задачи для самостоятельного решения: №1. Построить сечение прямоугольной призмы ABCDA1B1C1D1 плоскостью, проходящей через точки: №2. Построить сечение призмы ABCDA1B1C1D1, проходящей через P, N, E,F, M, K соответственно лежащие на рёбрах A1B1, B1C1, C1C, DC, AD и AA1 призмы. №3. Построить сечение призмы ABCDA1B1C1D1, проходящее через точки M,N,O,K соответственно принадлежащие сторонам CC1, DD1, AA1, BB1. №4. Постройте сечение четырехугольной призмы ABCDA1B1C1D1 плоскостью, проходящей через сторону основания и одну из вершин другого основания. №5. Точки M, N и P - точки на разных рёбрах четырёхугольной призмы ABCDA1B1C1D1. Постройте сечение проходящее через эти точки. Пятиугольная призма № 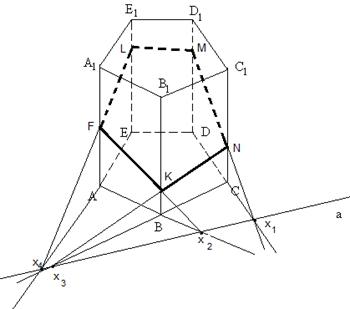 1. Построить сечение призмы ABCDEA1B1C1D1E1 плоскостью α, которая задана следом a в плоскости (ABC) основания призмы и точки M, принадлежащей ребру DD1. 1. Построить сечение призмы ABCDEA1B1C1D1E1 плоскостью α, которая задана следом a в плоскости (ABC) основания призмы и точки M, принадлежащей ребру DD1.Построение: 1) соединим точки L и M т.к. они лежат в одной плоскости EDE1D1. 2) продлим прямые: LF, NK, MN, FK, AB, CB 3) получим MNPFL – искомое сечение. № 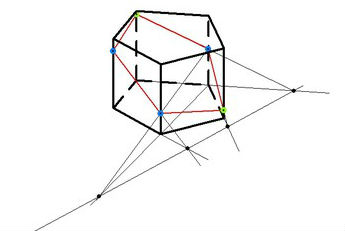 2. Построить сечение прямой пятиугольной призмы плоскостью заданной тремя точками выбранными произвольно на ее боковых ребер. 2. Построить сечение прямой пятиугольной призмы плоскостью заданной тремя точками выбранными произвольно на ее боковых ребер.Построение: 1)задана призма 2) заданы точки (синие) M, N, K. 3)проведём вспомогательные линии (используя метод следа) 4) определена прямая в плоскости основания, которая является пересечением сечения и плоскости основания 5)получены остальные точки (зеленые) P, Q 6) искомое сечение - MNPKQ. №3. 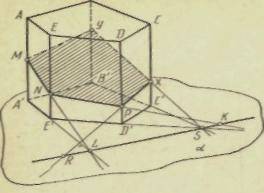 Построить сечение пятиугольной призмы плоскостью, заданной тремя точками, лежащими на боковых ребрах призмы. Построить сечение пятиугольной призмы плоскостью, заданной тремя точками, лежащими на боковых ребрах призмы. Построение: 1)Выберем плоскость А'В'С нижнего основания за основную плоскость а, а направление боковых ребер — за направление проектирования на основную плоскость. При таком выборе основной плоскости и направления проектирования изображение призмы является полным, т. е. все элементы призмы (грани, ребра и вершины) заданы на чертеже, что легко проверить. Так как изображение является полным, то требуемое в задаче построение осуществимо на чертеже. 2) (L С MN, α) и (К С NP, α) Þ (MNP ∩ α = KL); 3) R С C'D', KL; (R С C D') и (CD' С С CD) => (R С С CD); (R С KL) и (KL MNP)=>(R С MNP); 4) (P С MNP, С CD) и (R С MNP, C'CD)=>(MNP ∩C'CD= PR); (X С C'C, PR) Þ (X = MNP ∩ C C); 5) S С B'C, KL; (S С B'C) и (B'C B'BC) => (S С B'BC); (S С KL) и (KL С MNP)=>(S С MNP); 6) (XMNP,B'BC)и(SСMNP,B'BC)=>(XS=MNP∩B'BC); 7) (Y С XS, B'B)=>(Y С MNP, B'B). 8) MNPXY — искомое сечение. №4. 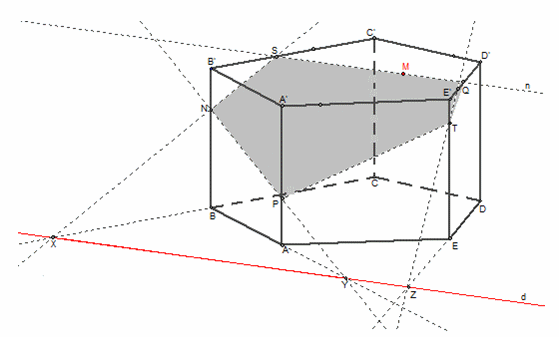 Построить сечение (M, d) призмы. Точка М принадлежит верхнему основанию, прямая d лежит в плоскости нижнего основания. Построить сечение (M, d) призмы. Точка М принадлежит верхнему основанию, прямая d лежит в плоскости нижнего основания.Построение: N' — проекция N, M' — проекция M; 2) NM ∩ N'M' = X; KX ∩ BC = T, KX ∩ DA = Y; TM ∩ CC' = H, TM ∩ B'C' = Z; ZN ∩ C'D' = P; NY ∩ AA' = F; THPNFK — искомое сечение. № 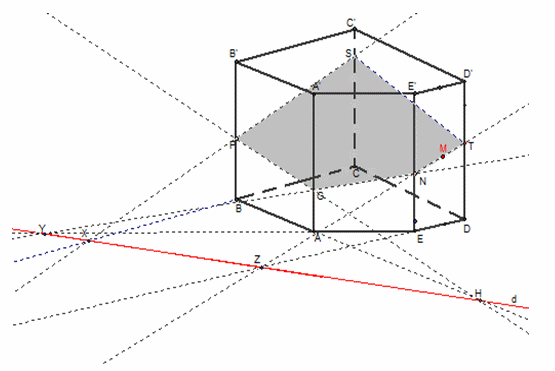 5. Построить (M, d) сечение призмы. Точка М принадлежит боковому ребру, прямая d лежит в плоскости нижнего основания. 5. Построить (M, d) сечение призмы. Точка М принадлежит боковому ребру, прямая d лежит в плоскости нижнего основания. Построение: 1) CB ∩ d = X, EA ∩ d = Y, DE ∩ d = Z, BA ∩ d = H; 2) MZ ∩ EE' = N, MZ ∩ DD' = T; 3) NY ∩ AA' = G; 4) GH ∩ BB' = P; 5) PX ∩ CC' = S; 6) PSTNG — искомое сечение. Задачи для самостоятельного решения: №1. Дано: Пятиугольная призма ABCDEA1B1C1D1E1; Точки K, M, P. Построить: Сечение плоскостью, проходящей через точки K, M, P. №2. Построить сечение пятиугольной призмы плоскостью, проходящей через точку на боковом ребре параллельно двум скрещивающимся ребрам. №3. Построить сечение пятиугольной призмы плоскостью, проходящей через точку на боковом ребре параллельно скрещивающимся диагоналям двух смежных граней. №4. Построить сечение пятиугольной призмы плоскостью, проходящей через три точки, одна из которых лежит в плоскости верхнего основания, а две другие – на несмежных боковом ребре и ребре нижнего основания. №5. Построить сечение пятиугольной призмы плоскостью, проходящей через сторону AE основания и точку K взятую на боковом ребре DD1. (точку K взять так чтобы в сечении получился пятиугольник). Шестиугольная призма № 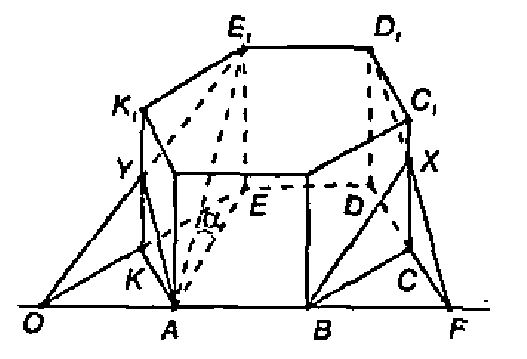 1. В правильной шестиугольной призме, у которой боковые грани — квадраты, проведите плоскость через сторону нижнего основания и противолежащую ей сторону верхнего основания. Сторона основания равна а. Найдите площадь построенного сечения. 1. В правильной шестиугольной призме, у которой боковые грани — квадраты, проведите плоскость через сторону нижнего основания и противолежащую ей сторону верхнего основания. Сторона основания равна а. Найдите площадь построенного сечения. Построение: 1) Данное сечение проходит через основание АВ и E1D1. Обозначим точку пересечения прямых АВ и DC точка F. Тогда F принадлежит плоскости сечения, а также плоскости CC1D1C. 2) Так что проведем прямую D1F, которая пересечет ребро СС1 в некоторой точке X. Далее, продолжим прямые ЕК и АВ до их пересечения в точке О. Эта точка принадлежит плоскости сечения, а также грани KK1E1E. 3)Тогда проведем прямую ОЕ1, которая пересечет ребро КК1 в некоторой точке Y. Шестиугольник 4)ABXD1E1Y — искомое сечение. №2. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, найдите расстояние от точки C до прямой A1B1. Точка C и прямая A1B1.выделены на призме красным цветом. Построение: 1 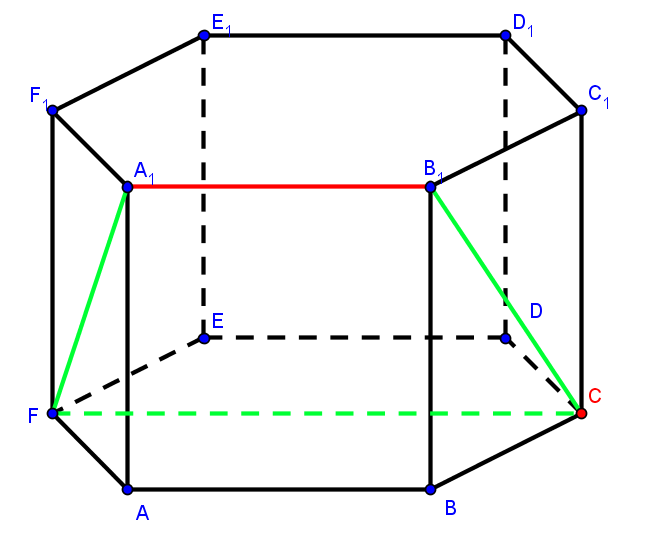 ) Основанием правильной шестиугольной призмы является правильный шестиугольник ABCDEF. В правильном шестиугольнике диагональ FC параллельна стороне AB. В свою очередь, у правильной призмы ребра AB и A1B1 также параллельны. ) Основанием правильной шестиугольной призмы является правильный шестиугольник ABCDEF. В правильном шестиугольнике диагональ FC параллельна стороне AB. В свою очередь, у правильной призмы ребра AB и A1B1 также параллельны. 2) Из теоремы о двух прямых, параллельных третьей, следует параллельность прямых FC и A1B1, обеспечивающая рассматриваемому четырехугольнику свойства плоской фигуры-трапеции. 3) Вследствие равенства боковых граней правильной призмы оказываются равными и боковые ребра трапеции. В результате расстояние от исходной точки, принадлежащей нижнему основанию трапеции, до верхнего основания трапеции совпадает с расстоянием между ее основаниями или, короче – с высотой B1G. 4) Искомое сечение - A1B1CF. №3. 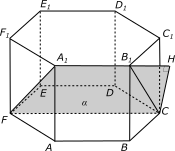 В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1все ребра равны 1. Постройте сечение призмы плоскостью, проходящей через точки A1, B1 и C. Построение: 1) Пусть α плоскость образованная точками A1, B1 и C. Ребро А1В1принадлежит α . 2) Точки В1 и С принадлежат секущей плоскости α и грани (ВВ1С1С), следовательно α пересекается с гранью (ВВ1С1С) по прямой В1С. 3)Прямая FC параллельна прямой А1В1, точки А1, В1 и С принадлежат плоскости α , следовательно F∈α . Точки F и С принадлежат плоскости α и грани (ABCDEF), следовательно α пересекается с гранью (ABCDEF) по прямой FC. 4) Точки F и A1 принадлежат секущей плоскости α и грани (AA1F1F), следовательно α пересекается с гранью (AA1F1F) по прямой F1A1. 5) Таким образом трапеция A1B1CF и будет сечением призмы плоскостью α , которой принадлежат точки A1,B1 и C. № 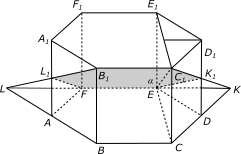 4. В правильной шестиугольной призме A…F1 все ребра равны 10. Постройте сечение призмы плоскостью, проходящей через точки E, B1 и C1. 4. В правильной шестиугольной призме A…F1 все ребра равны 10. Постройте сечение призмы плоскостью, проходящей через точки E, B1 и C1.Построение: 1) Секущая плоскость α определяется точками E, B1 и C1 не лежащими на одной прямой (теорема о существовании и единственности плоскости, проходящей через три точки). 2) Найдем прямые, по которым α пересекает плоскости граней шестиугольной призмы. B1 и C1 общие точки плоскости α и ребраB1C1, которое является общим для граней A1B1C1D1E1F1 и BB1C1C, следовательно эти плоскости пересекаются по прямой B1C1. 3) Прямая FE параллельна прямой B1C1 и точки E, B1 и C1принадлежат плоскости α, следовательно точка F так же принадлежит α. F и E общие точки плоскости α и ребра FE, которое является общим для граней ABCDEF и FF1E1E, следовательно эти плоскости пересекаются по прямой FE. 4)Точка K — точка пересечения прямых CD и EF. Точка K принадлежит CD, а значит принадлежит плоскости грани CC1D1D. Точки C1 и K принадлежат плоскости CC1D1D, следовательно C1K также принадлежит этой плоскости. 5) Прямые C1K и D1D принадлежат плоскости CC1D1D и не параллельны друг другу, следовательно они пересекаются в точке K1. Точки C1 и K принадлежат плоскостиα, следовательно все точки прямой C1K, в том числе K1, также принадлежат α. 6) C1 и K общие точки плоскостиα и плоскости грани CC1D1D, следовательно эти плоскости пересекаются по прямой C1K. K1 и E общие точки плоскости α и плоскости грани EE1D1D, следовательно эти плоскости пересекаются по прямой EK1. 7) Аналогичным способом построим точки L и L1, а также прямые пересечения плоскости α, и граней шестиугольной призмы. 8) B1C1K1EFL1 - искомое сечение призмы. №5. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Постройте сечение призмы плоскостью, проходящей через точки F1, A и C. П 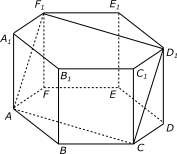 остроение: остроение:1) Секущая плоскость α определяется точками A, C, F1, не лежащими на одной прямой (теорема о существовании и единственности плоскости, проходящей через три точки). 2)Найдем прямые, по которым α пересекает плоскости граней шестигранника. A и C общие точки плоскости α и плоскости грани ABCDEF, следовательно эти плоскости пересекаются по прямой AC. A и F1 общие точки плоскости α и плоскости грани AFF1A1, следовательно эти плоскости пересекаются по прямой AF1. 2)Прямая F1D1 параллельна AC и точки A, C и F1 принадлежат плоскости α, следовательно точка D1 так же принадлежит α. F1 и D1 общие точки плоскости α и плоскости грани A1B1C1D1E1F1, следовательно эти плоскости пересекаются по прямойF1D1. 3)D1 и C общие точки плоскости α и плоскости грани CDD1C1, следовательно эти плоскости пересекаются по прямой D1C. 4)F1D1CA - искомое сечение призмы. Задачи для самостоятельного решения: №1. Построить сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1 плоскостью, проходящей через точки A, B’, F’. №2. Построить сечение правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1 плоскостью, проходящей через точки F’, B’, D’. №3. Построить сечение шестиугольной призмы плоскостью проходящей через точки M,N,P расположенных на гранях FF1E1E, AA1B1B и EE1D1D. №4. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все рёбра которой равны 1, постройте и найдите площадь сечения проходящее через вершины B, C и E1. №5. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все рёбра которой равны 1, постройте и найдите площадь сечения, проходящее через вершины F, C и D1. |
