|
|
УРОК. Сценарий урока алгебры в 9 классе (учебник Ю. Н. Макарычева и др.) Составитель Чернышев Э. Н., учитель математики мбоу сош 3
ПЕРЕСТАНОВКИ И ИХ ПРИМЕНЕНИЕ В РЕШЕНИИ КОМБИНАТОРНЫХ ЗАДАЧ
Сценарий урока алгебры в 9 классе
(учебник Ю.Н.Макарычева и др.)
Составитель : Чернышев Э.Н., учитель математики
МБОУ СОШ №3
г.Красный Сулин Ростовской области
8(86367)52337, eduardlaw@yandex.ru
Цели урока:
1.Формирование у обучающихся представлений о способах и методах математического описания реальных процессов и явлений.
2.Содействовать развитию вычислительной культуры школьников.
3.Способствовать овладению школьниками навыками математического моделирования.
Формируемые компетенции:
способность строить и преобразовывать математические модели жизненных (бытовых) процессов;
способность анализировать совокупности однородных объектов;
способность к построению логических умозаключений.
Уровень сложности :
средний; для общеобразовательных классов
Условия применения :
наличие у обучающихся опыта изучения элементов комбинаторики в 5-8 классах;
использование учебника алгебры авторов Макарычева Ю.Н. и др.;
достаточный уровень мотивации обучающихся к изучению математики .
Возможные риски:
несформированность навыков аналитического мышления у обучающихся;
непонимание обучающимися математики как науке о методах познания окружающего мира, что может проявиться в «развлекательном» восприятии комбинаторных задач;
данный раздел («Комбинаторика») в школьной математике введен недавно, у многих учителей нет должного опыта его преподавания, методы изучения нового материала могут быть исполнены не полностью, фрагментарно.
Тип урока :
урок изучения и закрепления нового материала.
Ход урока:
Номер этапа
|
Деятельность обучающихся
|
Деятельность учителя
|
|
Участвуют в беседе. Отвечают на вопросы,
|
Фронтальная беседа с элементами опроса:
На предыдущем уроке мы познакомились с комбинаторными задачами, с общими определениями комбинаторики и теории вероятностей и комбинаторным правилом умножения.
Выполним задания устно :
1.Составьте все возможные комбинации (выборки) из трех учеников (Иванов, Петров, Сидоров) по два элемента в каждой выборке. (Ответ : Иванов и Сидоров; Иванов и Петров; Сидоров и Петров).
2.Если объект А можно выбрать х способами, а объект В – у способами, то сколько способов существует для выбора объекта А и объекта В одновременно ? (Ответ : х+у.)
3.Из города А в город В ведут три дороги, а из города В в город С ведут четыре дороги. Сколько различных вариантов маршрутов из города А в город С можно составить ? (Ответ: 12).
4.Имеются три цифры : 2, 5 и 7. Сколько различных двухзначных чисел можно составить из этих цифр без повторения их в записи числа ? (Ответ.6).
5. Имеются три цифры : 2, 0 и 7. Сколько различных двухзначных чисел можно составить из этих цифр без повторения их в записи числа ? (Ответ.4).
6.При встрече 10 человек обменялись фотографиями. Сколько потребовалось фотографий ? (Ответ.90).
7.При встрече 10 человек обменялись рукопожатиями. Сколько всего было сделано рукопожатий ? (Ответ. 45).
В какой форме могут быть построены математические модели ?
в форме таблицы;
в форме выражения;
в виде формулы;
в виде уравнения;
в виде неравенства;
в виде графика;
в виде схемы или чертежа.
Какие формы математической модели мы сегодня встретим на уроке ?
|
|
Выполняют задания математического диктанта :
№
|
ЗАДАНИЕ
|
ОТВЕТ
|
1
|
Из цифр 1, 4, 2 составьте наибольшее трехзначное число.
|
421
|
2
|
Из цифр 1, 0, 7 составьте наименьшее трехзначное число.
|
107
|
3
|
Сколько двузначных чисел можно составить из цифр 9, 7, 4 без повторения их в записи числа ?
|
6
|
4
|
Сколько двузначных чисел можно составить из цифр 8, 4, 9 с повторением их в записи числа ?
|
9
|
5
|
Сколько различных двузначных чисел можно составить из цифр 3, 7, 0 без повторения их в записи числа ?
|
4
|
6
|
Сколько различных двузначных чисел можно составить из цифр 3, 7, 0 с повторением их в записи числа ?
|
6
|
7
|
Из города А в город В ведут две дороги, А из города В в город С – пять дорог. Сколько различных маршрутов можно проложить из города А в город С через город В ?
|
10
|
8
|
В шахматном турнире участвуют 11 человек. Каждый из них сыграл с каждым по одной партии. Сколько партий было сыграно ?
|
55
|
9
|
При встрече 20 человек обменялись рукопожатиями. Сколько было сделано рукопожатий ?
|
190
|
10
|
Сколько различных трехзначных чисел можно получить из цифр 6, 9, 3 без повторения их в записи числа ?
|
6
|
Время выполнения – 4 минуты.
|
Диктует задания мат.диктанта. Организует проверку выполненных заданий. Варианты проверки :
1.Предложить продублировать ответы в рабочей тетради. Собрать выполненные задания. Предъявить правильные ответы. Оценить успешность класса.
2.Содрать выполненные задания. Предложить проверить задания двум ученикам-экспертам. Огласить и обсудить результаты.
3.Взаимопроверка (в парах).
4.Самопроверка (правильные ответы предъявить на экране).
|
|
Составляют четырехзначные числа:
1234
1243
1342
1324
1423
1432
|
2341
2314
2143
2134
2431
2413
|
3421
3412
3142
3124
3241
3214
|
4132
4123
4321
4312
4213
4231
|
Данная таблица является моделью результата решения задачи.
|
Предлагает обучающимся составить из цифр 1, 2, 3, 4 все возможные четырехзначные числа без повторения цифр в записи числа .
Сколько всего таких чисел можно получить (24).
1.Сколькими способами можно выбрать первую цифру ? (4)
2.Сколькими способами можно получить вторую цифру из оставшихся ? (3)
3.Сколькими способами можно получить третью цифру из оставшихся ? (2)
4.Сколькими способами можно получить четвертую цифру ? (1)
Проверьте равенство :
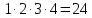
Какой вывод можно сделать ?
|
|
С помощью текста п.31 учебника выполните следующие задания :
Найдите и запишите определение перестановки.
Узнайте, что называют факториалом числа n.
Запишите произведение первых n натуральных чисел (в форме выражения).
Запишите формулу для нахождения числа перестановок.
Вычислить : 1!=______; 2!=______; 3!=_______; 4!=______; 5!=________; 6!=______.
Решите уравнение 2х!=240.
|
Изучение теоретического материала с элементами модульной технологии.
Контрольные вопросы :
1.Какие комбинации (выборки) называют перестановками ?
2.Что такое «эн факториал» и как его найти?
3.По какой формуле находят число перестановок ?
4.Приведите примеры комбинаций, которые являются перестановками.
5.Из букв 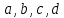 составляют различные комбинации (выборки). Какие из них являются перестановками ? составляют различные комбинации (выборки). Какие из них являются перестановками ?
Ответ : перестановки во втором столбике.
|
|
Участвуют в обсуждении решений задач.
|
Задача № 1
Сколько различных пятизначных чисел можно составить из цифр 0, 2, 4, 6 и 8, при условии, что цифры в записи числа не повторяются ?
Решение.
Из цифр 0, 2, 4, 6 и 8 можно получить 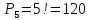 перестановок. Из них надо исключить те перестановки, которые начинаются с 0, так как натуральное число не может начинаться с нуля. Число таких перестановок равно числу перестановок цифр 2, 4, 6 и 8, т.е. перестановок. Из них надо исключить те перестановки, которые начинаются с 0, так как натуральное число не может начинаться с нуля. Число таких перестановок равно числу перестановок цифр 2, 4, 6 и 8, т.е. 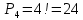 . Таким образом, искомое количество пятизначных чисел равно . Таким образом, искомое количество пятизначных чисел равно 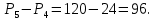
Ответ. 96.
Задача № 2
Имеется десять различных книг, из которых шесть – учебники. Сколькими способами можно расставить эти книги на полке так, чтобы все учебники стояли рядом ?
Решение.
Будем рассматривать все шесть учебников как один объект. Тогда на полке надо расставить пять книг (объектов). Число таких комбинаций равно 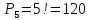 . К каждой из этих комбинаций учебники можно расставить различными способами. Количество таких способов равно . К каждой из этих комбинаций учебники можно расставить различными способами. Количество таких способов равно 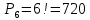 . По комбинаторному правилу умножения все десять книг можно разместить . По комбинаторному правилу умножения все десять книг можно разместить 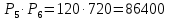 способами. способами.
Ответ. 86400.
Задача № 3
Сколько среди четырехзначных чисел, составленных из цифр 7, 6, 5, 0 (без их повторения), которые кратны 15 ?
Решение.
Из данных цифр можно составить 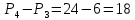 различных четырехзначных чисел без повторения цифр в их записи. различных четырехзначных чисел без повторения цифр в их записи.
Заметим, что сумма предложенных цифр равна 18, т.е. любое четырехзначное число, составленное из этих цифр (без их повторения в записи числа), будет кратно трем. Чтобы полученные числа были кратны 15, необходимо, чтобы они были кратны не только числу 3, но и числу 5, т.е. оканчивались на 0 или на 5 . Число таких чисел равно 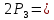 12. Таким образом, искомое количество равно 12. Таким образом, искомое количество равно 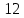 . .
Ответ. 12.
|
|
1.Сколькими способами можно расставить на книжной полке 5 различных книг ? (Ответ: 120).
2.Сколько различных шестизначных чисел можно составить из цифр 1, 4, 2, 9, 5 и 7 без повторения их в записи числа? (Ответ: 720).
3. Сколько различных шестизначных чисел можно составить из цифр 0, 4, 2, 9, 5 и 7 без повторения их в записи числа? (Ответ: 600).
4.Вычислить:
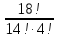 (Ответ : 3060) (Ответ : 3060)
5.Что больше и во сколько раз :
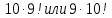 . .
(Ответ. Больше второе число в 9 раз).
6.Шесть мальчиков, в число которых входят Саша и Ваня, становятся в ряд. Найти число возможных комбинаций, если:
а) Саша должен находиться в начале ряда; (Ответ : 120)
б) Саша должен находиться в начале ряда, а Ваня – в конце ряда; (Ответ: 24)
в) Саша и Ваня должны стоять рядом. (Ответ : 48).
|
Решение задач. Решение задач выполняетсяПриложение)'> на доске с подробным разбором каждого решения.
Для обучающихся, успешно справляющихся с заданиями, даются индивидуальные задания (Приложение)
|
|
Тестовое задание :
№
|
ВОПРОС, ЗАДАНИЕ
|
А
|
В
|
С
|
Верный ответ
|
1
|
Сколькими способами можно разместить на четырехместной скамье четырех учеников ?
|
6
|
24
|
120
|
В
|
2
|
Число 720 является значением выражения…
|
120!
|
5!
|
6!
|
C
|
3
|
7! больше чем 5! …
|
в 35 раз
|
в 6 раз
|
в 42 раза
|
С
|
4
|
Из Красного Сулина в Новошахтинск ведут две дороги, а из Новошахтинска в Шахты – три дороги. Сколько маршрутов существует для проезда из Красного Сулина в Шахты через Новошахтинск ?
|
6
|
5
|
12
|
А
|
5
|
Сколько различных четырехзначных чисел можно составить из цифр 9, 8, 7 и 6 без повторения их в записи числа ?
|
24
|
120
|
30
|
А
|
6
|
Найти значение выражения 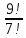
|
8
|
504
|
72
|
С
|
7
|
Сколько различных четырехзначных чисел можно составить из цифр 7, 5, 0 и 3 без их повторения в записи числа ?
|
24
|
18
|
3
|
В
|
8
|
Сколько среди четырехзначных чисел, составленных из цифр 2,5,8 и 9 (без их повторения) таких, которые начинаются с цифры 5 ?
|
24
|
6
|
3
|
В
|
9
|
Пять мальчиков, среди которых Иван и Саша, становятся в ряд. Найти число возможных комбинаций, если Иван должен стоять первым, а Саша – вторым.
|
6
|
24
|
18
|
А
|
10
|
Пять мальчиков, среди которых Иван и Саша, становятся в ряд. Найти число возможных комбинаций, если Иван и Саша должны стоять вместе.
|
6
|
18
|
24
|
С
|
Отлично
|
Хорошо
|
Удовл.
|
Неуд.
|
Кол-во верных ответов
|
10
|
9-8
|
7-5
|
4-0
|
|
Выдает тестовые задания. Контролирует ход и самостоятельность их выполнения. При необходимости дает направляющие примеры.
|
|
в форме таблицы;
в форме выражения;
в виде формулы;
|
Какие математические модели мы строили сегодня на уроке ?
|
|
Домашнее задание.
Выучить определение перестановки (стр. 176) и формулу для вычисления числа перестановок (стр. 177).
Выполнить решение задач № 741, № 744 с подробной записью решения.
|
Комментирует домашнее задание; указывает на возможные затруднения при выполнении заданий.
|
Приложение
Индивидуальные задания для обучающихся
Карточка № 1
|
Что больше и во сколько раз : 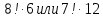 ? ?
Вычислить значение выражения 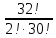 . .
Сколькими способами можно расставить на полке 15 книг, из которых 7 книг – поэтические сборники, так, чтобы эти сборники стояли рядом ?
Сократить дробь 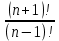
В расписании на понедельник семь уроков : алгебра, геометрия, физика, биология, физкультура, история и информатика. Сколькими способами можно составить расписание на этот день так, чтобы два урока математики были первыми ?
|
Карточка № 2
|
Что больше и во сколько раз : 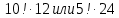 ? ?
Вычислить значение выражения 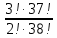 . .
Сколькими способами можно расставить на полке 17 книг, из которых 12 книг – поэтические сборники, так, чтобы эти сборники стояли рядом ?
Сократить дробь 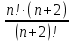 . .
В расписании на понедельник семь уроков : алгебра, геометрия, физика, биология, физкультура, история и информатика. Сколькими способами можно составить расписание на этот день так, чтобы физкультура и геометрия были рядом ?
|
Карточка № 3
|
Что больше и во сколько раз : 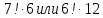 ? ?
Вычислить значение выражения 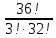 . .
Сколькими способами можно расставить на полке 11 книг, из которых 7 книг – поэтические сборники, так, чтобы эти сборники стояли рядом ?
Сократить дробь 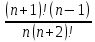 . .
Восемь мальчиков, в числе которых Никита и Артем, становятся в ряд. Найти число возможных комбинаций, если Никита и Артем должны стоять рядом ?
|
Карточка № 4
|
Что больше и во сколько раз : 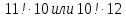 ? ?
Вычислить значение выражения 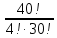 . .
Сколькими способами можно расставить на полке 13 книг, из которых 5 книг – поэтические сборники, так, чтобы эти сборники стояли рядом ?
Решить уравнение 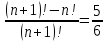 . .
Девять мальчиков, в числе которых Никита и Артем, становятся в ряд. Найти число возможных комбинаций, если Никита и Артем должны стоять рядом ?
|
Карточка № 5
|
Что больше и во сколько раз : 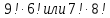 ? ?
Вычислить значение выражения 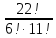 . .
Сколькими способами можно расставить на полке 14 книг, из которых 8 книг – поэтические сборники, так, чтобы эти сборники стояли рядом ?
Решить уравнение 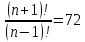 . .
В расписании на понедельник семь уроков : алгебра, геометрия, физика, биология, физкультура, история и информатика. Сколькими способами можно составить расписание на этот день так, чтобы физкультура и биология были рядом ?
|
Литература :
Алгебра. 9 класс : учеб. для общеобразоват. Учреждений / [Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова]; под ред. С.А.Теляковского.-М.:Просвещение, 2008-2011.
|
|
|
 Скачать 45.81 Kb.
Скачать 45.81 Kb.
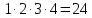
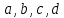 составляют различные комбинации (выборки). Какие из них являются перестановками ?
составляют различные комбинации (выборки). Какие из них являются перестановками ?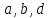
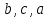
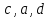
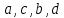
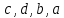
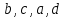
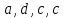
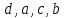
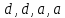
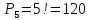 перестановок. Из них надо исключить те перестановки, которые начинаются с 0, так как натуральное число не может начинаться с нуля. Число таких перестановок равно числу перестановок цифр 2, 4, 6 и 8, т.е.
перестановок. Из них надо исключить те перестановки, которые начинаются с 0, так как натуральное число не может начинаться с нуля. Число таких перестановок равно числу перестановок цифр 2, 4, 6 и 8, т.е. 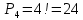 . Таким образом, искомое количество пятизначных чисел равно
. Таким образом, искомое количество пятизначных чисел равно 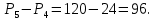
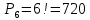 . По комбинаторному правилу умножения все десять книг можно разместить
. По комбинаторному правилу умножения все десять книг можно разместить 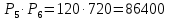 способами.
способами.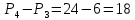 различных четырехзначных чисел без повторения цифр в их записи.
различных четырехзначных чисел без повторения цифр в их записи.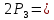 12. Таким образом, искомое количество равно
12. Таким образом, искомое количество равно 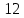 .
.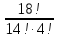 (Ответ : 3060)
(Ответ : 3060)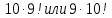 .
.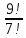
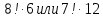 ?
?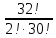 .
.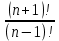
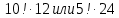 ?
?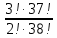 .
.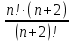 .
.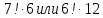 ?
?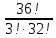 .
.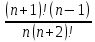 .
.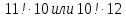 ?
?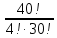 .
.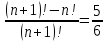 .
.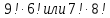 ?
?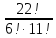 .
.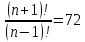 .
.