|
|
Сейсморазведка Хмелевской 1 половина. Сейсморазведка 10. Физикогеологические основы сейсморазведки
где 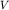 - скорость той или иной волны ( - скорость той или иной волны (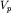 или или 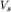 ), ), 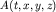 - амплитуда или иное возмущение сигнала, распространяющееся в среде ( - амплитуда или иное возмущение сигнала, распространяющееся в среде (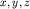 ) на разных временах ) на разных временах  после его возбуждения. Решение этого уравнения с использованием граничных условий очень сложно и его удается выполнить лишь для простых моделей сред. Значительно проще решать кинематические задачи, т.е. определять время прихода той или иной волны (прямой, отраженной, преломленной и др.) для известной модели, зная лишь положение источника и момент возбуждения упругой волны. Традиционно простейшим результатом решения прямой задачи является получение уравнения годографа, или аналитического выражения для после его возбуждения. Решение этого уравнения с использованием граничных условий очень сложно и его удается выполнить лишь для простых моделей сред. Значительно проще решать кинематические задачи, т.е. определять время прихода той или иной волны (прямой, отраженной, преломленной и др.) для известной модели, зная лишь положение источника и момент возбуждения упругой волны. Традиционно простейшим результатом решения прямой задачи является получение уравнения годографа, или аналитического выражения для 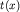 с дальнейшим построением годографа - графика зависимости времени прихода той или иной волны ( с дальнейшим построением годографа - графика зависимости времени прихода той или иной волны ( ) от расстояния от пункта возбуждения до пункта приема ( ) от расстояния от пункта возбуждения до пункта приема ( ). ).
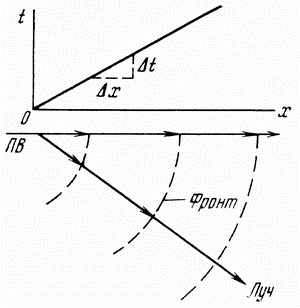
Самой простой прямой задачей сейсморазведки является получение годографа прямой волны, т.е. задачи, которую в других геофизических методах называют задачей о нормальном поле (см. рис. 4.2). Очевидно, что время прихода прямой волны после создания упругого импульса в пункте возбуждения или взрыва (ПВ) равно 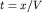 . Поэтому линейный годограф имеет вид прямой линии. По наклону прямой линии можно определить скорость . Поэтому линейный годограф имеет вид прямой линии. По наклону прямой линии можно определить скорость 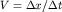 . .
|
Рис. 4.2. К выводу уравнения прямой волны
|
10.3.2. Прямая и обратная задача отраженной волны для двухслойной среды с наклонной границей раздела.
1. Прямая задача. Прямая задача сейсморазведки методом отраженных волн (МОВ) сводится к получению уравнения годографа над разрезом с известными мощностями слоев и скоростями распространения волн. Простейшим является двухслойный разрез с однородным изотропным верхним слоем и скачком акустической жесткости на наклонной границе с подстилающим полупространством.
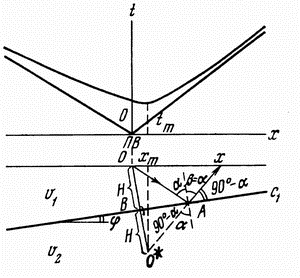
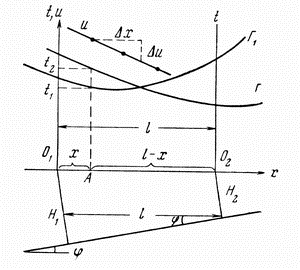
Пусть под однородной покрывающей средой со скоростью распространения упругих волн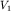 расположена вторая среда со скоростью расположена вторая среда со скоростью 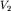 , а угол разделяющей их плоской границы равен , а угол разделяющей их плоской границы равен  (рис. 4.3). Если на границе раздела сред выполняется условие (рис. 4.3). Если на границе раздела сред выполняется условие 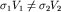 , то образуется однократная отраженная волна с углом отражения \gamma, равным углу падения , то образуется однократная отраженная волна с углом отражения \gamma, равным углу падения  . Требуется найти уравнение годографа, т.е. установить теоретическую зависимость времени прихода волны . Требуется найти уравнение годографа, т.е. установить теоретическую зависимость времени прихода волны  от расстояния от расстояния  , скорости распространения волны в перекрывающем слое , скорости распространения волны в перекрывающем слое 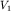 , эхо-глубины (глубины по нормали к отражающей границе) залегания отражающего контакта Н и его угла наклона , эхо-глубины (глубины по нормали к отражающей границе) залегания отражающего контакта Н и его угла наклона  . .
|
Рис. 4.3. К выводу уравнения годографа отраженной волны над двухслойным разрезом
|
Время прихода отраженной волны в точку  профиля наблюдения равно профиля наблюдения равно 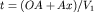 . Пусть О^{*} - мнимый пункт взрыва, или точка, расположенная на перпендикуляре к границе так, что . Пусть О^{*} - мнимый пункт взрыва, или точка, расположенная на перпендикуляре к границе так, что 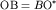 . Так как треугольники . Так как треугольники 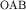 и и 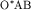 равны, а равны, а 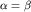 и и 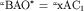 , то отрезки , то отрезки 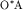 и и 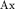 лежат на одной линии и лежат на одной линии и
Из прямоугольного треугольника 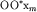 имеем имеем
Итак,
Это и есть уравнение линейного годографа однократно отраженной волны.
Можно показать, что полученное уравнение является уравнением гиперболы. В самом деле, из уравнения годографа можно получить
Это гипербола, действительная ось которой параллельна оси  и смещена на и смещена на 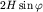 по оси по оси  . .
Из уравнения годографа можно найти его характерные точки:
Легко показать, что при 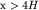 годограф отраженной волны асимптотически приближается к годографу прямой волны. годограф отраженной волны асимптотически приближается к годографу прямой волны.
Если в уравнении годографа для точек профиля, расположенных от пункта возбуждения по восстанию пласта, при выражении 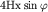 стоит знак "минус", то, как легко показать, для точек по падению пласта должен стоять знак "плюс". стоит знак "минус", то, как легко показать, для точек по падению пласта должен стоять знак "плюс".
Таким образом, решение прямой задачи метода отраженных волн для двухслойного однородного разреза приводит к следующему уравнению годографа:
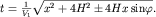
|
(4.6)
|
2. Обратная задача. Обратная задача метода отраженных волн (МОВ) для модели наклонного контакта двух сред сводится к определению скорости в перекрывающем слое 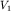 (в методе МОВ эту скорость для слоистой среды называют эффективной (в методе МОВ эту скорость для слоистой среды называют эффективной 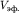 ) и геометрических параметров разреза ( ) и геометрических параметров разреза (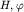 ). Обратная задача решается различными способами на основе анализа уравнения годографа (4.6). ). Обратная задача решается различными способами на основе анализа уравнения годографа (4.6).
Рассмотрим простейшие из них.
А. Определение эффективных скоростей в перекрывающей толще по годографам отраженных волн способами постоянной разности и встречных годографов. Способ постоянной разности при обработке одиночных годографов. Взяв две точки годографа, удаленные на расстояние m, запишем, используя (4.6), для них уравнения:
Вычтя из второго уравнения первое и обозначив 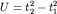 , получим: , получим:
Отсюда, положив 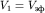 , можно найти , можно найти 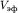 как угловой коэффициент прямой в новой системе координат как угловой коэффициент прямой в новой системе координат  и и 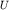 . В самом деле, продифференцировав это уравнение, получим . В самом деле, продифференцировав это уравнение, получим 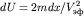 . Учтя, что для прямой линии . Учтя, что для прямой линии 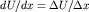 , легко получить формулу для расчета: , легко получить формулу для расчета:
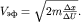
|
(4.7)
|
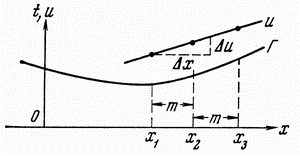
При практическом применении полученной формулы поступают следующим образом. На годографе выбирается несколько пар точек (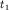 и и 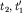 и и 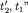 и и 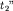 ), расположенных на постоянном расстоянии m друг от друга. Для каждой пары времен находится функция ), расположенных на постоянном расстоянии m друг от друга. Для каждой пары времен находится функция 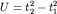 , соответствующая значению , соответствующая значению 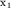 , и строится график функции , и строится график функции 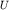 от от  (рис. 4.4). Взяв приращение (рис. 4.4). Взяв приращение 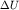 для какого-то для какого-то 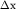 , легко рассчитать , легко рассчитать 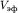 по формуле (4.7). по формуле (4.7).
|
|
а
|
б
|
Рис. 4.4. Определение эффективной скорости по данным МОВ способом постоянной разности (а) и встречных годографов (б)
|
Способ двух встречных годографов. Если есть два встречных годографа (рис. 4.4, б), то уравнения годографов для одной точки профиля имеют вид
Вычтя из второго уравнения первое и учтя, что 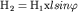 , получим , получим
Введя обозначения 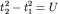 и заменив все члены правой части, не содержащие и заменив все члены правой части, не содержащие  , на , на  , можно записать: , можно записать:
Последнее уравнение является уравнением прямой в системе координат 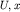 . .
Отсюда:
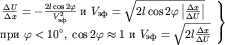
|
(4.8)
| |
|
|
 Скачать 1.1 Mb.
Скачать 1.1 Mb.



