Сейсморазведка Хмелевской 1 половина. Сейсморазведка 10. Физикогеологические основы сейсморазведки
 Скачать 1.1 Mb.
|
|
При  , что означает приход волны сначала к удаленным, а затем к близким к пункту взрыва точкам наблюдения. При  и  , что соответствует случаю, когда головная преломленная волна не сможет выйти на поверхность и работы методом МПВ невозможны. Поэтому этот метод может применяться для изучения не очень крутых структур, т.е. при углах падения, меньших 45 .Преломленная волна на удалении  от пункта взрыва всегда приходит раньше отраженной и прямой волн и ее удобно регистрировать в области первых вступлений. Применяется также корреляционный метод преломленных волн (КМПВ), когда выделение преломленных волн производится и в последующих вступлениях.Как показано выше, годограф волны, преломленной на плоской границе двух сред, прямолинеен. Однако, если преломляющая граница криволинейна, то и годограф приобретает криволинейную форму. Это объясняется тем, что угол выхода сейсмической радиации  и кажущаяся скорость  меняется при изменении угла наклона границы ( ) по профилю наблюдений, что приводит к изменению угла наклона годографа.Как отмечалось в 10.1.4, если в среде скорость упругих волн возрастает с глубиной, что может наблюдаться, например, при смене литологии или из-за увеличения давления, то возникают рефрагированные волны. Механизмы образования рефрагированных и скользящих преломленных волн имеют определенное сходство. С увеличением скорости с глубиной критический угол падения увеличивается и рефрагированные волны будут проходить во втором слое по дугообразным лучам (4.1, в). Выходя на поверхность земли, рефрагированные волны регистрируются подобно головным преломленным. Годографы преломленных и рефрагированных волн сходны между собой, и их распознавание имеет большое значение, так как позволяет избавиться от ошибок при интерпретации результатов сейсморазведки. 3. Обратная задача метода преломленных волн. Обратная задача метода преломленных волн (МПВ) над наклонной границей двух сред сводится к определению скоростей в верхнем (  ) и нижнем ( ) слоях и геометрических параметров разреза (Н, \varphi). Ее решают различными способами, основанными на анализе уравнения годографа (4.8) - (4.10). Как показывает практика интерпретации МПВ, наиболее надежно решить обратную задачу можно, имея встречные годографы (Г1 и Г2), которые получаются из двух точек взрыва О1 и О2, находящихся на концах изучаемого профиля (рис. 4.8).
А. Определение граничной скорости по разностному годографу. Имея два встречных годографа, можно построить разностный годограф:  , где  и  - время прихода головной преломленной волны в точку х по первому и второму (встречному) годографу,  - время во взаимных точках, т.е. время прихода волны из О1 в О2 или из О2 в О1 (см. рис. 4.8). Легко видеть, что путь головной волны из пункта взрыва О1 в точку О2 и, наоборот, из пункта взрыва О2 в точку О1 одинаков, а значит, время во взаимных точках по встречным годографам одинаково и постоянно для данного интервала О1О2 (рис. 4.8).Взяв производную от уравнения разностного годографа, получим  , где  - угловой коэффициент разностного годографа, равный обратной скорости, т.е.
Отсюда
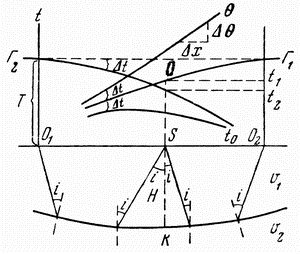
Таким образом, граничная скорость может быть определена по наклону разностного годографа  . При углах наклона, меньших 10 - 15 ,  .Б. Определение скорости в перекрывающем слое. Скорость упругих волн в перекрывающем слое (толще)  может быть оценена по точкам пересечения годографов прямой и головных преломленных волн:  , где  и  - координаты точек пересечения.Однако более точно  получается по данным метода отраженных волн (10.3.2).В. Построение преломляющей границы способом нулевого времени. Одним из простых и точных способов определения  и построения преломляющей границы является способ нулевого времени ( ).Для любой точки  , где имеются два встречных годографа (см. рис. 4.8), можно найти некоторую функцию  , которая равна времени на пункте взрыва  . В самом деле,  . Отсюда, считая границу на участке СD плоской и опустив из S перпендикуляр на СD, получим
Из треугольника CSK:  . Учитывая, что  , получим:
Следовательно, для любой точки профиля, где имеются встречные годографы, можно найти фиктивное время , а затем и рассчитать
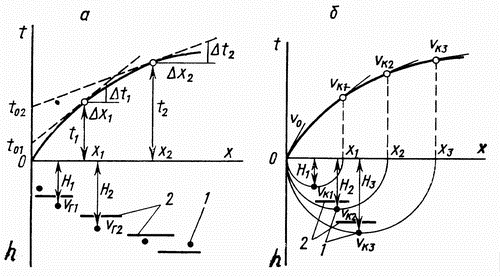
Практически применение способа сводится к следующему. Для любой точки х определяется величина  . От значения  по первому годографу измерителем откладывается  вверх (получаем точку разностного годографа  ) и вниз (получаем  ). Сделав подобные построения в нескольких (3 - 5) точках оси х и соединив точки  и , получаем разностный годограф  и линию  . По наклону разностного годографа находится граничная скорость  (при  ). Если угол  , то ее можно определить по формуле, приведенной выше ( ). Зная в каждой точке, по формуле (4.13) можно рассчитать эхо-глубину  .Проведя из нескольких точек х дуги радиусами и соединив их плавной касательной, получим искомую преломляющую криволинейную границу раздела. Для криволинейной границы не имеет смысла говорить об угле наклона , поскольку он разный в разных точках преломляющей границы.Приведенные прямые и обратные задачи МОВ и МПВ для двухслойного разреза являются основными задачами сейсморазведки, поскольку, заменив верхний слой (  ) толщей ( ), получаем практически одни и те же годографы. Решение кинематических прямых и обратных задач для отраженных, преломленных, рефрагированных, дифрагированных волн слоистых толщ (одномерные задачи - 1Д), сред с вытянутыми контактами (двухмерные задачи - 2Д) и для включений объектов (трехмерные задачи - 3Д) в аналитическом виде связано с большими математическими сложностями. 10.3.4. Принципы решения обратной задачи метода рефрагированных волн. Решение обратной задачи метода рефрагированных волн (МРВ) сложнее, чем преломленных. Они сводятся к построению скоростных разрезов или полей скоростей, на которых для каждой точки разреза известна скорость. Для разных законов изменения скоростей с глубиной разработаны различные приемы построения скоростных разрезов по годографам рефрагированных волн. Рассмотрим один из простых для среды с вертикальным градиентом скорости. Она принимается за слоисто-однородную, состоящую из бесконечно тонких горизонтальных слоев, в каждом из которых скорости постоянны, а на границах возрастают скачком, но таким образом, что чем глубже слой, тем выше скорость в нем (см. рис. 4.1). Для таких разрезов можно воспользоваться решением обратной задачи МПВ над многослойной средой. На годографе рефрагированной волны выбирается несколько (до 5) точек (  ) и в каждой из них проводится касательная (рис. 4.9). По пересечению касательных с осью времен определяются  , а по их наклону - кажущиеся скорости 
В 10.3.3 получено выражение для кажущейся скорости головной преломленной волны, которая в случае горизонтальной преломляющей границы (  ) равна  (здесь применена формула  ). Поэтому можно записать  За среднюю скорость  в покрывающей среде над соответствующими преломляющими площадками с  принимается полученное эмпирическим путем выражение  , где  - скорость в покрывающей толще, если считать ее неградиентной;  По известным  и  можно определить глубину залегания преломляющих площадок:
Для практического построения скоростного разреза данным методом от точек профиля, расположенных в середине между пунктом возбуждения и расчетными точками  , вниз откладываются глубины  и у них записываются граничные скорости Если провести изолинии, то получим скоростной разрез. Построение скоростных разрезов описанными выше способами обычно выполняется на компьютерах.10.4. Основы теории сейсмоэлектрического метода Сущность сейсмоэлектрического метода сводится к возбуждению упругих волн с помощью взрывов или невзрывных источников и изучению как упругих волн, так и электромагнитных импульсов. Сейсмоэлектрические явления, на которых этот метод основан, объясняются, по крайней мере, двумя факторами: пьезоэлектрическим эффектом (ПЭЭФ) кристаллических горных пород и сейсмоэлектрическим эффектом (СЭЭФ) осадочных пород. 10.4.1. Пьезоэлектрический эффект. Пьезоэлектрический эффект представляет собой электрическую поляризацию, т.е. определенную ориентировку полярных молекул при механическом воздействии на вещество. Пьезоэлектрическая поляризация наблюдается как в монокристаллах некоторых диэлектриков (реже - полупроводников), так и в поликристаллических средах, какими являются горные породы. 10.4.2. Сейсмоэлектрический эффект. Сейсмоэлектрический эффект изучен значительно хуже, чем пьезоэлектрический, и наблюдается при прохождении сейсмических волн через осадочные влагосодержащие породы. Под действием упругой волны происходит смещение подвижной части двойных электрических слоев, существующих на твердых частицах этих пород. В результате создаются электрические потенциалы, природа которых примерно такая же, как и у потенциалов фильтрации (см. 7.2). Объясняется это тем, что интенсивность фильтрационного и сейсмоэлектрического полей пропорциональна разности давлений на концах капилляра. В первом случае оно постоянно и пропорционально скорости движения подземных вод через капилляры, а во втором - переменно и синхронно изменяется с прохождением упругой волны, меняющей давление на концах капилляров. Количественно сейсмоэлектрический эффект принято характеризовать пьезоэлектрическим модулем (см. 10.2.4). |
