Проект Секреты куба. Секреты куба. Секреты куба
 Скачать 4.09 Mb. Скачать 4.09 Mb.
|
|
Исследовательская творческая работа «Секреты куба» . Подготовили обучающиеся 6 класса Стекольникова Мария, Дягелева Полина Руководитель учитель математики Пастухова Н.А. СОДЕРЖАНИЕ: ВВЕДЕНИЕ………………………………………………………… 2 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 1. Основные элементы куба……………………………….. 3 2. Развертка куба. Задачи с разверткой куба …………… 3-5 3. Метод трех проекций. Задачи на построение проекций 5-7 4. Кубические единицы измерения………………………… 7-8 5. Моделирование куба…………………………………….. 8 КУБ В ПРИРОДЕ И ИСКУССТВЕ Кристаллы соли ……………………………………… 9 Куб в архитектуре …………………………………… 9 Куб в живописи ……………………………………… 10 ЗАКЛЮЧЕНИЕ…………………………………………………… 11 СПИСОК ЛИТЕРАТУРЫ………………………………………… 11  ВВЕДЕНИЕ. В философии Платона: Куб - символизирует Землю, как самый "устойчивый". В своей деятельности человеку повсюду приходится сталкиваться с необходимостью изучать форму, размеры, взаимное расположение пространственных фигур. Подобные задачи решают и астрономы, имеющие дело с самыми большими масштабами, и физики, исследующие структуру атомов и молекул, и архитекторы, возводящие здания. Окружающий нас мир устроен таким образом, что ни один человек в своей жизни не обойдется без пространственного представления предметов. Куб - это фигура, которую мы встречаем не только на уроках геометрии, но и в изобразительном искусстве. Куб является одним из более применяемых геометрических объектов в повседневной жизни человека. С раннего детства мы знакомы с объемной фигурой – куб. Широкое распространение куб нашел для производства детских игрушек. За счет своих правильных форм он помогает развиваться детям. Кубики отлично развивают не только координацию, воображение, но при этом задействуют практически все мышцы рук, что прекрасно развивает мелкую моторику малыша. В младшем возрасте дети играют в настольные игры, используя игральный кубик, на каждой из шести граней которого нанесены числа от 1 до 6. Для интеллектуального развития венгерский скульптор и преподаватель архитектуры Эрне Рубик изобрел механическую головоломку Кубик Рубика. Ни одни геометрические тела не обладают таким совершенством и красотой, как правильные многогранники, к которым относится и куб. Но так ли проста эта фигура - куб? Что мы знаем о ней? Цель исследования: изучить куб, развертки куба, способы моделирования куба. В связи с поставленной перед нами целью необходимо решить ряд задач: Изучить литературу, интернет-ресурсы о понятии куба, модели куба, куба в природе и повседневной жизни. Сделать подборку задач, связанных с кубом. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Основные элементы куба. К 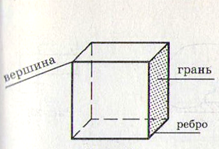 уб - прямоугольный параллелепипед, у которого все три измерения равны. Куб (др.-греч. Κύβος ) или правильный гексаэдр(«правильный шестигранник» от др.-греч. ξάς «шесть» и др.-греч. δρα «седалище, основание») правильный многогранник, каждая грань которого представляет собой квадрат. уб - прямоугольный параллелепипед, у которого все три измерения равны. Куб (др.-греч. Κύβος ) или правильный гексаэдр(«правильный шестигранник» от др.-греч. ξάς «шесть» и др.-греч. δρα «седалище, основание») правильный многогранник, каждая грань которого представляет собой квадрат.Куб это прямоугольный параллелепипед, у которого все ребра равны. Куб - правильный шестигранник, т. е. тело, ограниченное шестью квадратами. Куб тело прямоугольной формы с одинаковыми гранями.
Куб имеет 8 вершин, 6 граней, 12 ребер. Если куб сделан не из прозрачного материала, то некоторые грани и вершины мы не увидим, невидимые ребра изображают пунктирными линиями. При одной вершине находится 3 грани. Отрезок, соединяющий две противоположные вершины куба (наиболее удаленные друг от друга), называется ДИАГОНАЛЬЮ КУБА. Если ребро куба обозначить a , тогда Объем куба: V = a3 Площадь поверхности:S= 6a2 Развертка куба. Развертка куба – это оболочка, с ее помощью мы можем видеть куб со всех сторон. Развертка куба состоит из 6 граней или 6 равных квадратов. Существует 20 разверток куба. Задачи с разверткой куба. Упражнение 1 Нижняя грань куба черная, раскрась другим цветом верхнюю грань. Упражнение 2 Укажите на рис. 27 развертки куба. Ответ: 1, 2, 4, 6 – 9. Упражнение 3 Условимся боковые грани куба обозначать буквой Б, верхнюю – В, нижнюю Н. Расставьте на развертках куба буквы в соответствии с уже намеченными (рис. 28). Упражнение 4 Дана развертка куба (рис. 29). Какие из кубиков на рисунке 30, а – в можно из нее склеить? Ответ: а). Упражнение 5. На рисунке 22 изображены игральный кубик и его развертка. Какое число находится на: а) нижней грани куба; б) боковой грани слева; в) боковой грани сзади? Ответ: а)6; б)5; в)2. Упражнение 6. На рисунке 23 изображены два одинаковых игральных кубика. Какие числа изображено на их нижних гранях? Ответ: а)5; б)2. Упражнение 7. На рисунке 24 показаны игральный кубик и три развертки. Какие из них могут быть развертками именно этого кубика. Ответ: б). Упражнение 8. На развертке куба (рис. 31) пронумерованы его грани. Запишите парами номера противоположных граней: 1 и …, 2 и …, 3 и …. Запишите грани которые соседствуют с гранью 6. Упражнение 9. На видимых гранях куба (рис. 32, а) проставлены числа 1,2, 3. А на развертках (рис. 32, б, в) – два из названных чисел или одно. Расставьте на развертках куба числа 1,2,3, 4,5, 6 так, чтобы сумма чисел на противоположных гранях была равна 7. Метод проекций. Изображение пространственных фигур и их частей вызывает большие трудности, если не знать некоторые секреты. Что за странный куб мы увидели на рисунке 36? По изображению пространственной фигуры мы не всегда можем себе представить, как выглядит она со всех сторон. Для облегчения этой задачи используют МЕТОД ТРЕХ ПРОЕКЦИЙ. Этим методом пользуются инженеры, конструкторы, дизайнеры для изображения различных деталей. Это метод включает изображение проекций фигуры, увиденной спереди, сверху и слева: вид спереди, вид сверху и вид слева. 3.1. Задачи на построение проекций Упражнение 10 На рис. 33 мы смотрим на куб справа и сверху. На рисунке 34 проведите сплошные линии (видимые ребра) так, чтобы куб был «виден»: а) слева снизу; б) справа сверху; в) справа снизу. Упражнение 11 Сколько кубиков вы видите на рис. 37? Ответ: 6 или 7. Упражнение 12 На рис. 27 изображены три вида фигуры, сложенной из кубиков. Нарисуйте эту фигуру. Ответ: рис. 82 Упражнение 13 На рис. 28 показаны вид спереди и вид слева фигуры, сложенной из кубиков. Из какого наибольшего ( наименьшего) числа кубиков можно сложить эту фигуру? Ответ: из 10 (4). Упражнение 14 На рис.25, а изображена фигура, сложенная из 6 кубиков. На рис. 25, в показаны три вида этой фигуры: спереди, слева и сверху. Нарисуйте три вида для фигуры, изображенной на рис. 25, б. Ответ: рис. 81. Упражнение 15 По поверхности стеклянного куба проходит ломаная линия, сделанная из толстой проволоки. Рассмотрите ломанные и кривые линии на рис. 167 и начертите в каждом случае три проекции. Ответ: рис. 377. Упражнение 16 Даны проекции ломанных спереди, сверху и слева (рис. 168). Нарисуйте куб, а на его поверхности проволоку, из которой сделаны эти ломанные (общий вид). Ответ: рис. 378. 4. Кубические единицы измерения 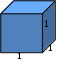 Важным свойством тела является его вместимость. Важным свойством тела является его вместимость.Вместимость фигуры характеризуют объемом. За единицу измерения объема принимают объем единичного куба. Единичный куб - это куб, длина ребра которого равна одной единице длины: 1 мм, 1 см, 1дм, 1м, 1км Объемы единичных кубов получают названия в зависимости от выбранной единицы длины ребра: кубический миллиметр (1 мм); кубический сантиметр(1 см3); кубический дециметр(1 дм3); кубический метр (1 м3); кубический километр (1 км3). Пример: Кубометр чистой воды при температуре её максимальной плотности (3,98 °C) и стандартном атмосферном давлении (101,325 кПа) имеет массу равную 1000 кг = 1 тонна. При 0 °C, температуре замерзания воды, он немного легче — 999,972 кг. Упражнение 17 Найдите объемы тел, состоящих из единичных кубов с ребром 1 см.      Моделирование куба Существуют различные способы моделирования куба. Первый: использовать развертку куба. Второй: плетение из трех полосок, разделенных на пять квадратов. Третий: используя оригами.  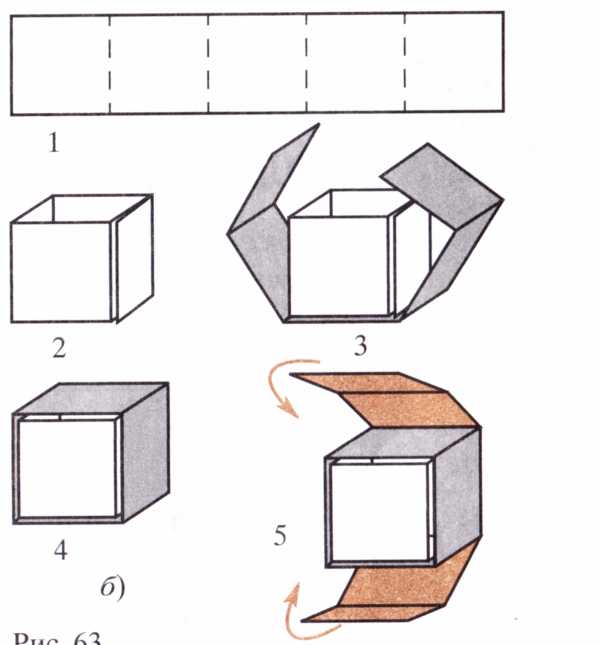  КУБ В ПРИРОДЕ И ИСКУССТВЕ Кристаллы соли Форму куба имеет монокристалл поваренной соли, Поваренная соль (NaCl) — пищевой продукт. Производится и используется после промышленной очистки минерала Галит (вещество — хлорид натрия), известного также под названием «каменная соль». Соль жизненно необходима всем живым существам. Она участвует в поддержании и регулировании водного баланса в организме.  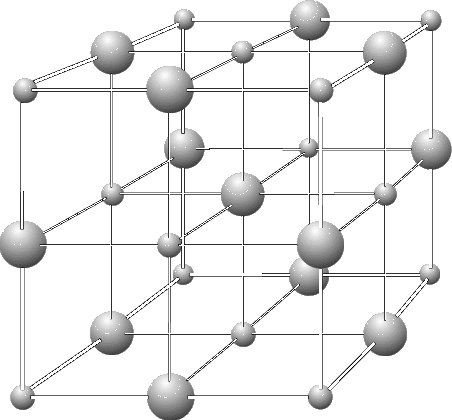 Куб в архитектуре С  точки зрения формы архитектура всегда была преимущественно кубической. По сути дела куб лежал в основе любой архитектурной формы нескольких последних тысячелетий. Многие современные здания вызывают восхищение, имея в своей основе куб или сочетание кубов. точки зрения формы архитектура всегда была преимущественно кубической. По сути дела куб лежал в основе любой архитектурной формы нескольких последних тысячелетий. Многие современные здания вызывают восхищение, имея в своей основе куб или сочетание кубов.ХАБИТАТ 67 в Монреале, Канада. Это сооружение спроектировал архитектор Моше Сафди. Хабитат 67 был выстроен специально для выставки Экспо-67, которая называлась "Человек и его мир" (словами Антуана де Сент-Экзюпери из романа "Планета людей"). Отель-кубвСловакии Дом-куб в Австралии.   Р  оттердам — архитектор наклонил обычный дом на 45 градусов так, что три грани куба смотрят в небо, а три — в землю. Живое воплощение идеи «посмотреть на обычное под другим углом». В каждом из таких кубиков три этажа, что позволяет не чувствовать никаких бытовых неудобств. оттердам — архитектор наклонил обычный дом на 45 градусов так, что три грани куба смотрят в небо, а три — в землю. Живое воплощение идеи «посмотреть на обычное под другим углом». В каждом из таких кубиков три этажа, что позволяет не чувствовать никаких бытовых неудобств.Куб в живописи Я  рчайшим примером художественного изображения многогранников в XX веке являются, конечно, графические фантазии Маурица Корнилиса Эшера (1898-1972), голландского художника, родившегося в Леувардене. Правильные геометрические тела - многогранники - имели особое очарование для Эшера. В его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов. рчайшим примером художественного изображения многогранников в XX веке являются, конечно, графические фантазии Маурица Корнилиса Эшера (1898-1972), голландского художника, родившегося в Леувардене. Правильные геометрические тела - многогранники - имели особое очарование для Эшера. В его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов.Наиболее интересная работа Эшера - гравюра "Звезды", на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров. В 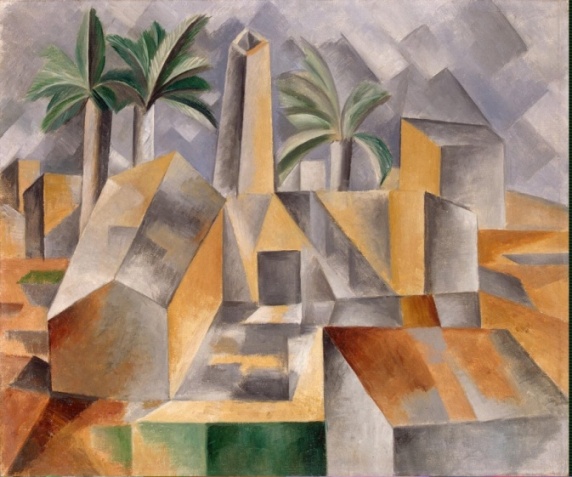 живописи начала ХХ века возникло модернистское направление - Кубизм (от фр. cubisme, произошло от cube - куб), которое выдвинуло на первый план формальную задачу конструирования объёмной формы на плоскости, сведя к минимуму изобразительно-познавательные функции искусства. Слово "кубисты" было употреблено в 1908 и 1909 французским критиком Л. Воселем как насмешливое прозвище группы художников, изображавших предметный мир в виде комбинации геометрических тел или фигур. Самый известный художник этого направления живописи: Пабло Пикассо (1881-1973). живописи начала ХХ века возникло модернистское направление - Кубизм (от фр. cubisme, произошло от cube - куб), которое выдвинуло на первый план формальную задачу конструирования объёмной формы на плоскости, сведя к минимуму изобразительно-познавательные функции искусства. Слово "кубисты" было употреблено в 1908 и 1909 французским критиком Л. Воселем как насмешливое прозвище группы художников, изображавших предметный мир в виде комбинации геометрических тел или фигур. Самый известный художник этого направления живописи: Пабло Пикассо (1881-1973).Русский художник Георгий Курасов, родившийся в 1958 году в советском Ленинграде, без сомнения, является одним из наиболее ярким представителем такого направления в живописи, как кубизм.   ЗАКЛЮЧЕНИЕ. В результате своей исследовательской работы мы узнали, что Пифагорейцы считали правильные многогранники божественными фигурами и использовали их в своих философских сочинениях. Их поражала красота, совершенство, гармония этих фигур. Куб – один из правильных многогранников. В архитектуре куб как символ стабильности использовался в качестве фундаментального камня-основания, а также в современной архитектуре как элемент модерна. Многие художники в своем творчестве использовали куб как элемент изображения, а также как особое течение в искусстве – кубизм. Мы изучили учебную литературу, интернет – ресурсы по теме «Куб». Это помогло нам больше узнать о способах изображения и моделирования куба, подобрать занимательные задания, которые можно использовать на уроках наглядной геометрии. Эти задания развивают пространственное воображение, что необходимо во многих профессиях: инженера, конструктора, токаря, дизайнера, архитектора. Мы расширили свои знания по моделированию, что позволило нам сделать различные модели куба. На основе всего мы сделали вывод, что самое прекрасное и совершенное приходит к нам от природы. СПИСОК ЛИТЕРАТУРЫ И ИНТЕРНЕТ - РЕСУРСЫ. Математический энциклопедический словарь/ «Советская Энциклопедия», 1988г. Учебник «Наглядная геометрия, 5-6 класс» И.Ф. Шарыгин, Л.Н. Ерганжиева, М: Дрофа, 2014. Задачи на смекалку. 5-6. И.Ф. Шарыгин, А.В. Шевкин, М: Просвещение, 2010. https://ru.wikipedia.org/wiki/%CA%F3%E1 https://yandex.ru/images/search?text=примеры картин кубизм&img_url=http%3A%2F%2Fic.pics.livejournal.com%2Fphilologist%2F23000738%2 https://yandex.ru/images/search?text=%D0%BA%D1%83%D0%B1%
|
