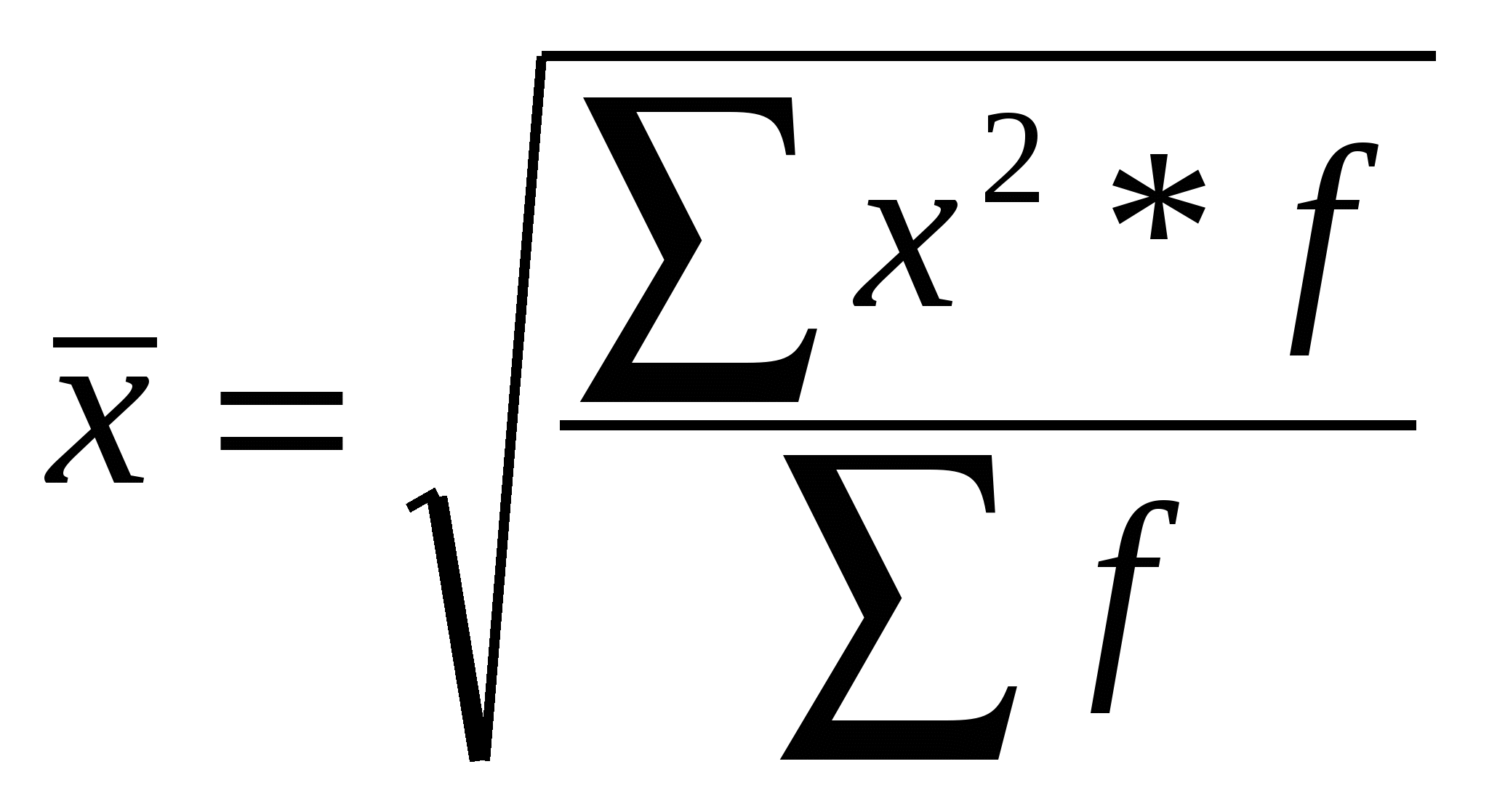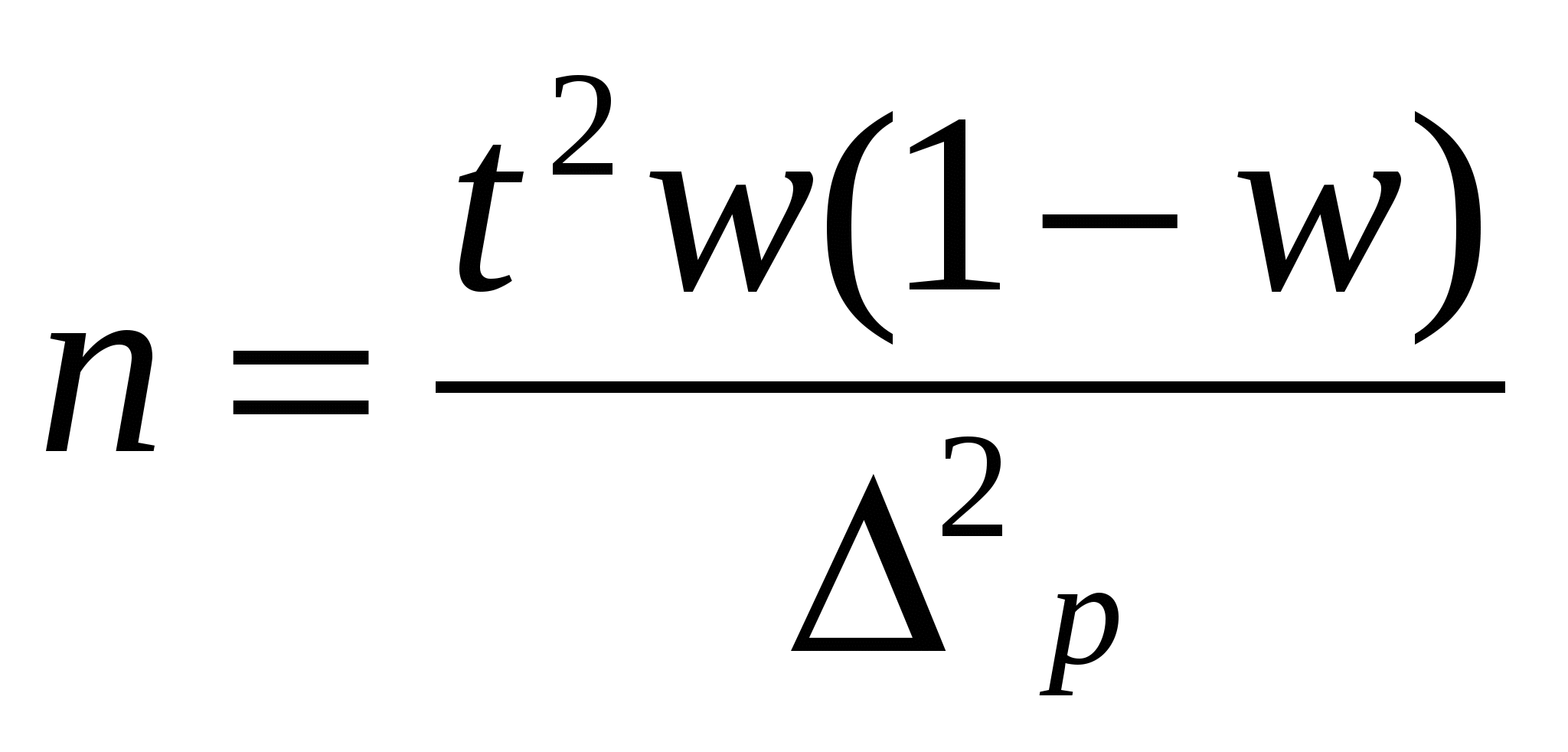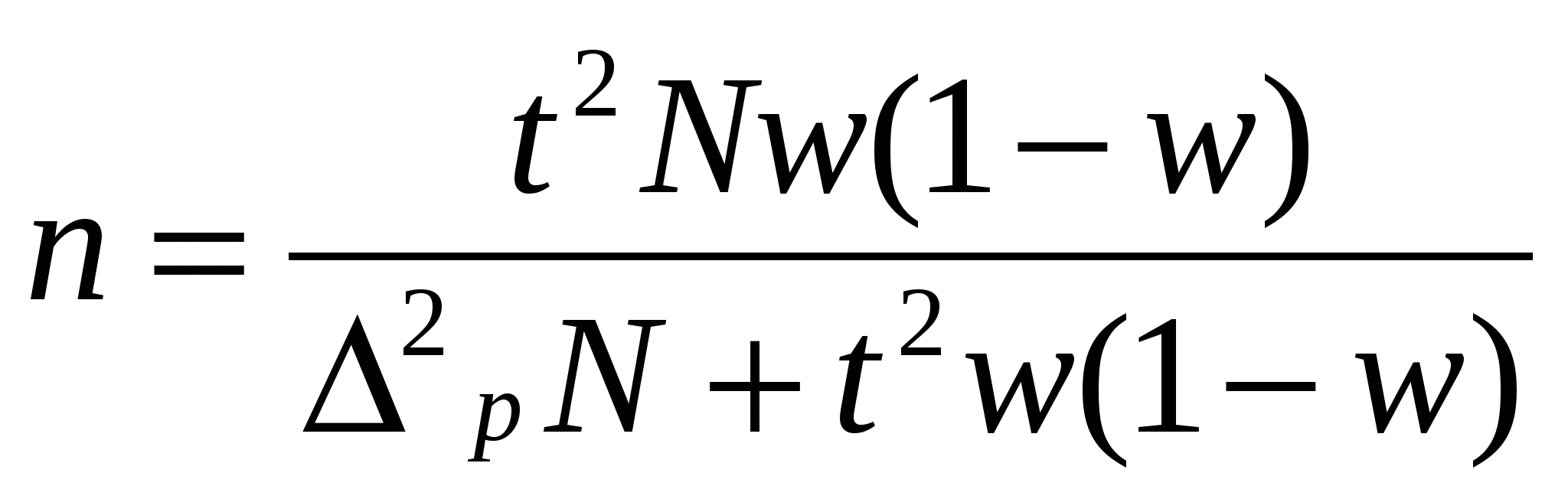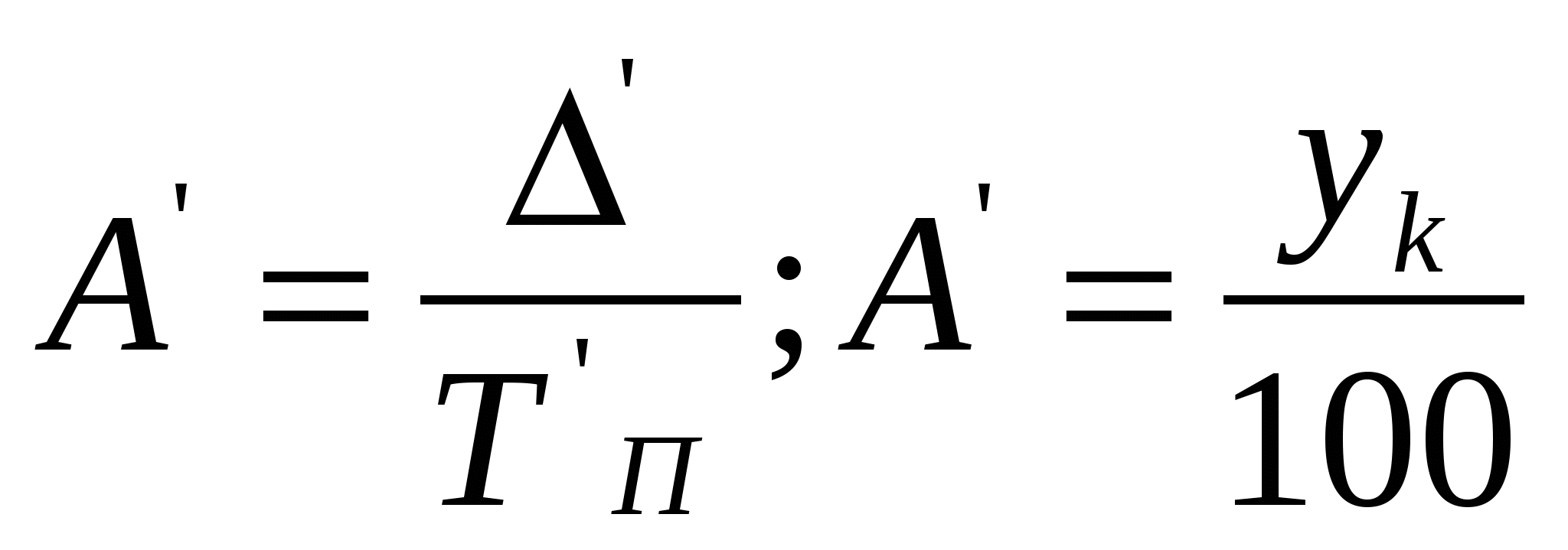Все формулы по статистике. Семестр 1 2 Группировка статистических данных и ее роль в анализе информации 2 Абсолютные, относительные, средние величины 2
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
|
Содержание Семестр 1 2 Группировка статистических данных и ее роль в анализе информации 2 Абсолютные, относительные, средние величины 2 Относительные величины 2 Средние величины 2 Статистические распределения и их характеристики 3 Показатели вариации (колеблемости) признака 4 Сложение дисперсий 4 Показатель асимметрии 5 Показатель эксцесса (островершинности) 5 Кривые распределения 5 Выборочное наблюдение 6 Формулы ошибок простой случайной выборки 7 Формулы для определения численности простой и случайной выборки 7 Типичная выборка 7 Серийная выборка 8 Малые выборки 8 Корреляционная связь 8 Уравнение регрессии 9 Ряды динамики 9 Показатели динамики 9 Средние показатели динамики 10 Тренды 10 Семестр 2 (Индексы) 11 Семестр 1Группировка статистических данных и ее роль в анализе информацииРавный интервал, величина интервала - Формула Стерджесса (величина интервала) - Абсолютные, относительные, средние величиныОтносительные величиныОтносительные величины (ОВ) динамики характеризуют изменение явления во времени. (Коэффициент роста) Темп роста – с переменной базой - С постоянной базой - ОВ планового задания - ОВ выполнения плана - ОВ динамики - ОВ структуры характеризуют долю отдельных частей в общем объеме совокупности (удельный вес) - 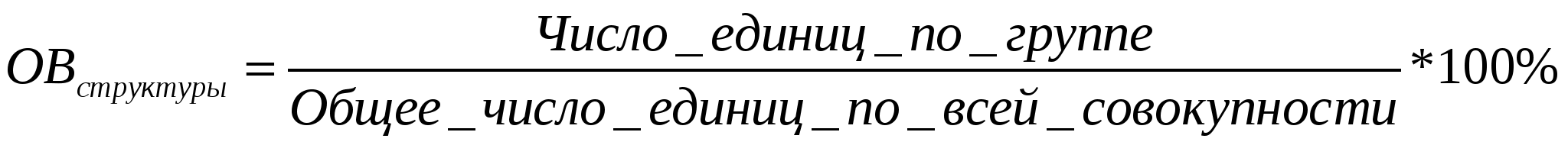 ОВ координации отражают отношение численности двух частей единого целого, т. е. показывают, сколько единиц одной группы приходится в среднем на одну, на 10 или на 100 единиц другой изучаемой совокупности. ОВ координации - ОВ наглядности (сравнения) отражают результаты сопоставления одноименных показателей, относящихся к одному и тому же периоду времени, но к разным объектам или территориям (например, сравнивается годовая производительность труда по 2-м предприятиям) ОВ сравнения - Средние величиныСтепенные средние общего типового расчета: Средняя степенная простая - 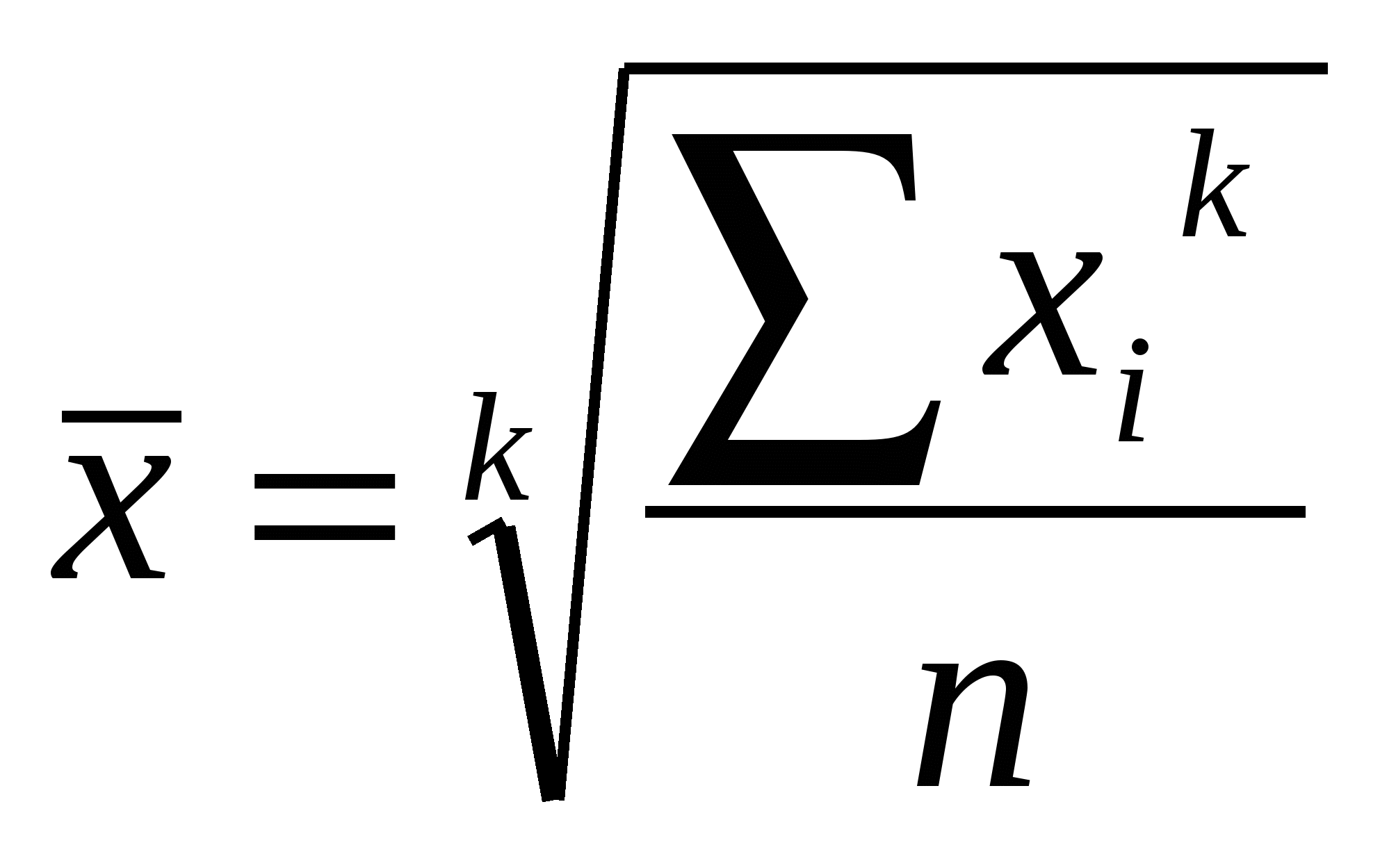 , , Средняя степенная взвешенная - 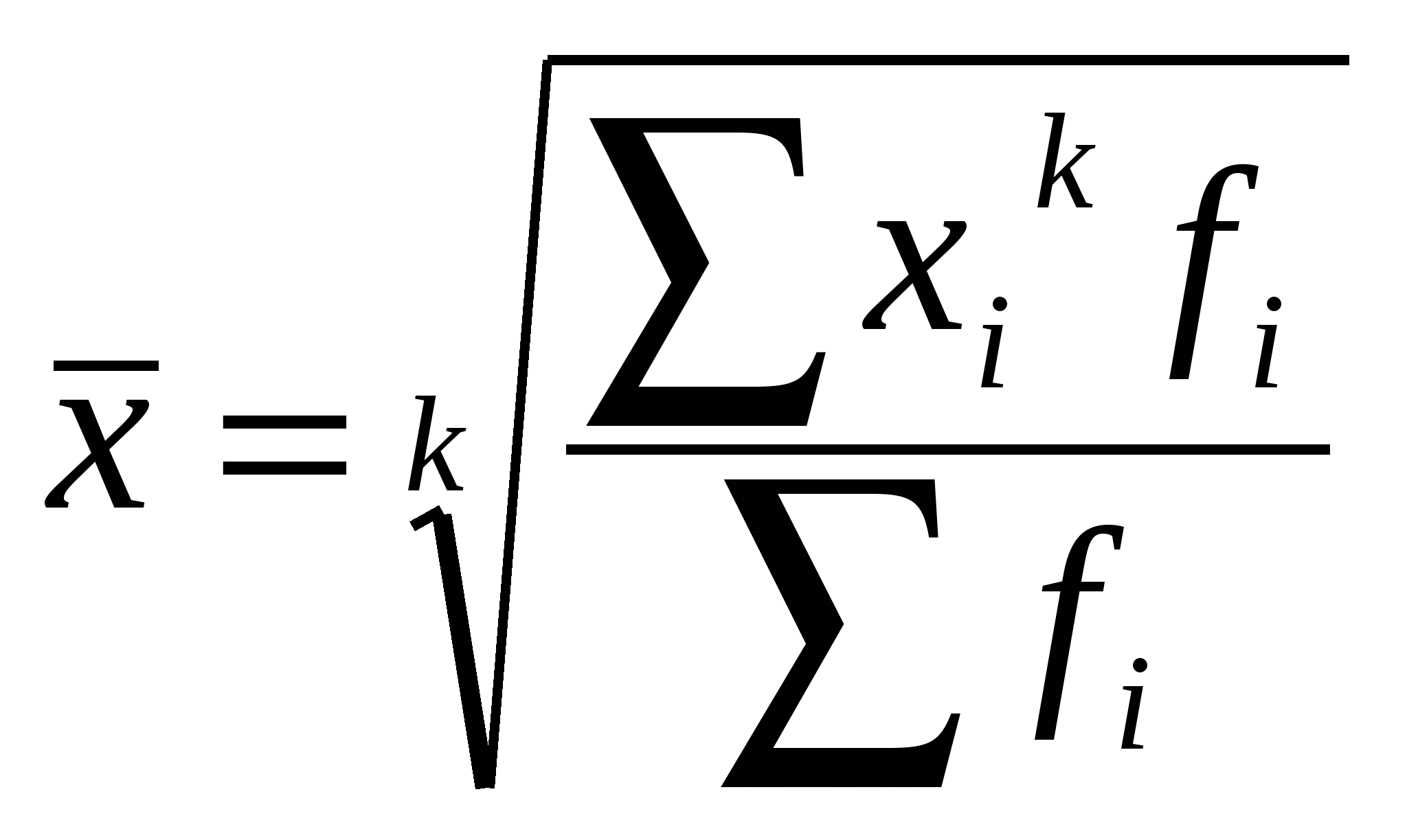 , fi – частота повторения индивидуального признака ( , fi – частота повторения индивидуального признака (
Гармоническая простая – когда небольшая совокупность и индивидуальные значения не повторяются. Используется, если исчисляем среднюю из обратных величин. Средняя квадратическая – для расчета среднего квадратического отклонения, являющегося показателем вариации признаков Средняя геометрическая простая – для вычисления среднего коэффициента роста (темпа) в рядах динамики, если промежутки, к которым относятся коэффициенты роста, одинаковы. Статистические распределения и их характеристикиМода – значение признака, которое наиболее часто встречается в совокупности 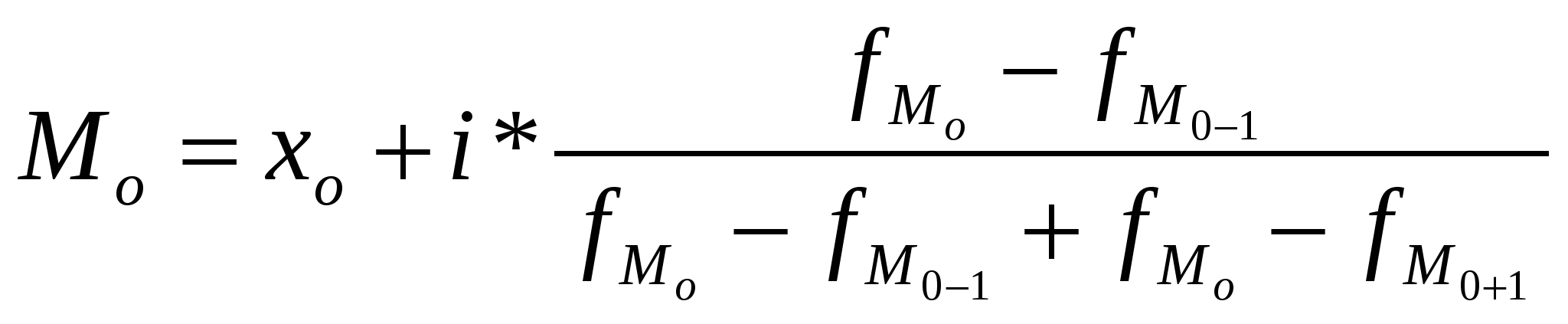 , , Медиана – значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части. 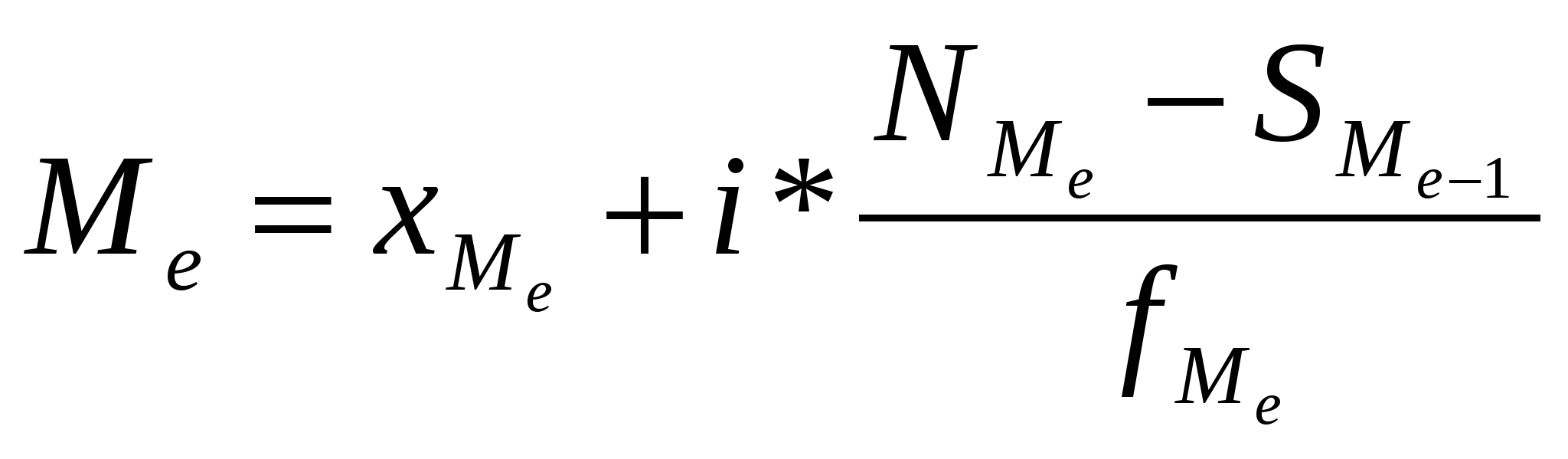 , , Квартель Дециль Показатели вариации (колеблемости) признакаСреднее линейное отклонение – на сколько в среднем отличаются индивидуальные значения признака от среднего его значения. -для несгруппированных данных (первичного ряда): -для вариационного ряда: Среднее квадратическое отклонение - для несгруппированных данных: - для вариационного ряда: 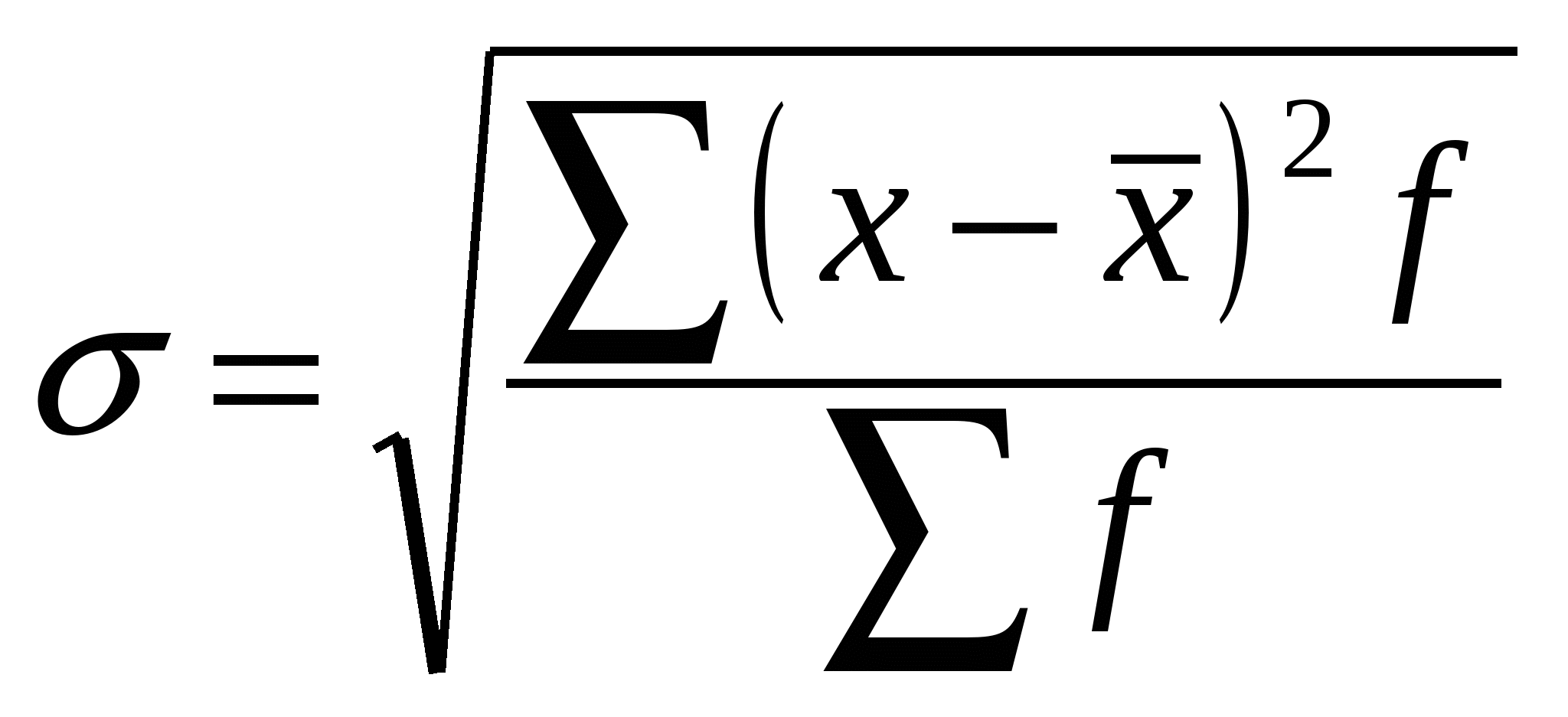 Дисперсия - для несгруппированных данных: - для вариационного ряда: Коэффициент вариации (используется для характеристики однородности совокупности по исследуемому признаку) Сложение дисперсийВеличина общей дисперсии ( Межгрупповая дисперсия ( 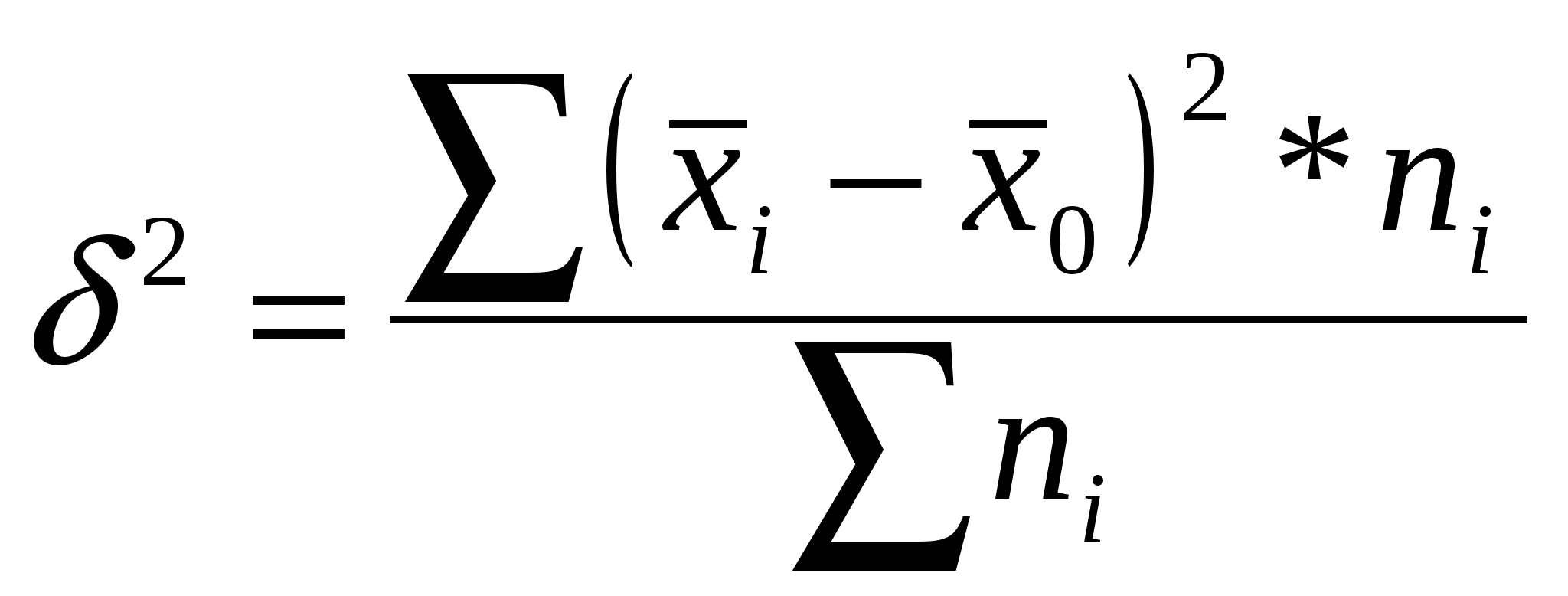 , ,Средняя внутригрупповая дисперсия ( 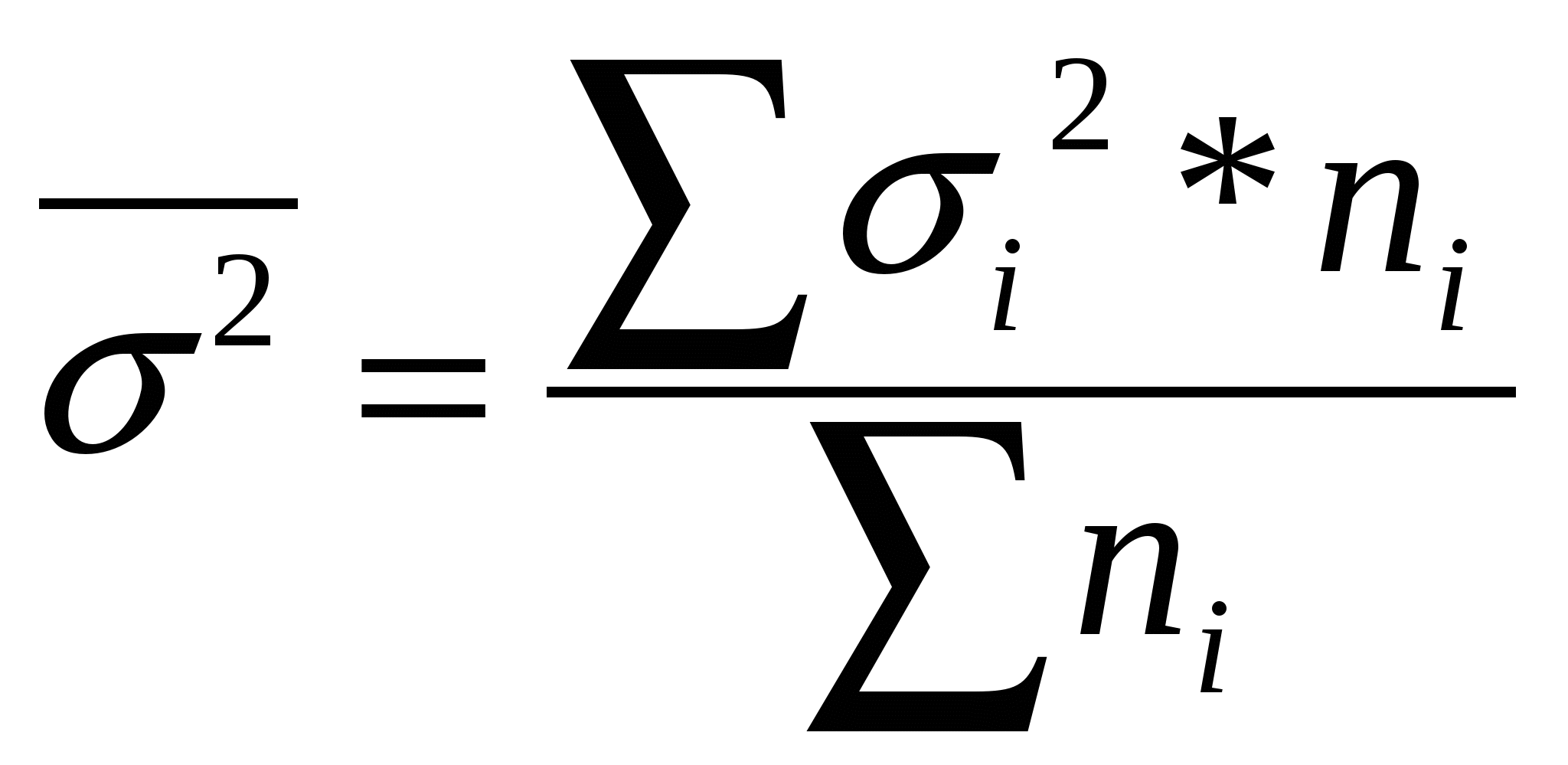 , где , где или Равенство: Корреляционное отношение 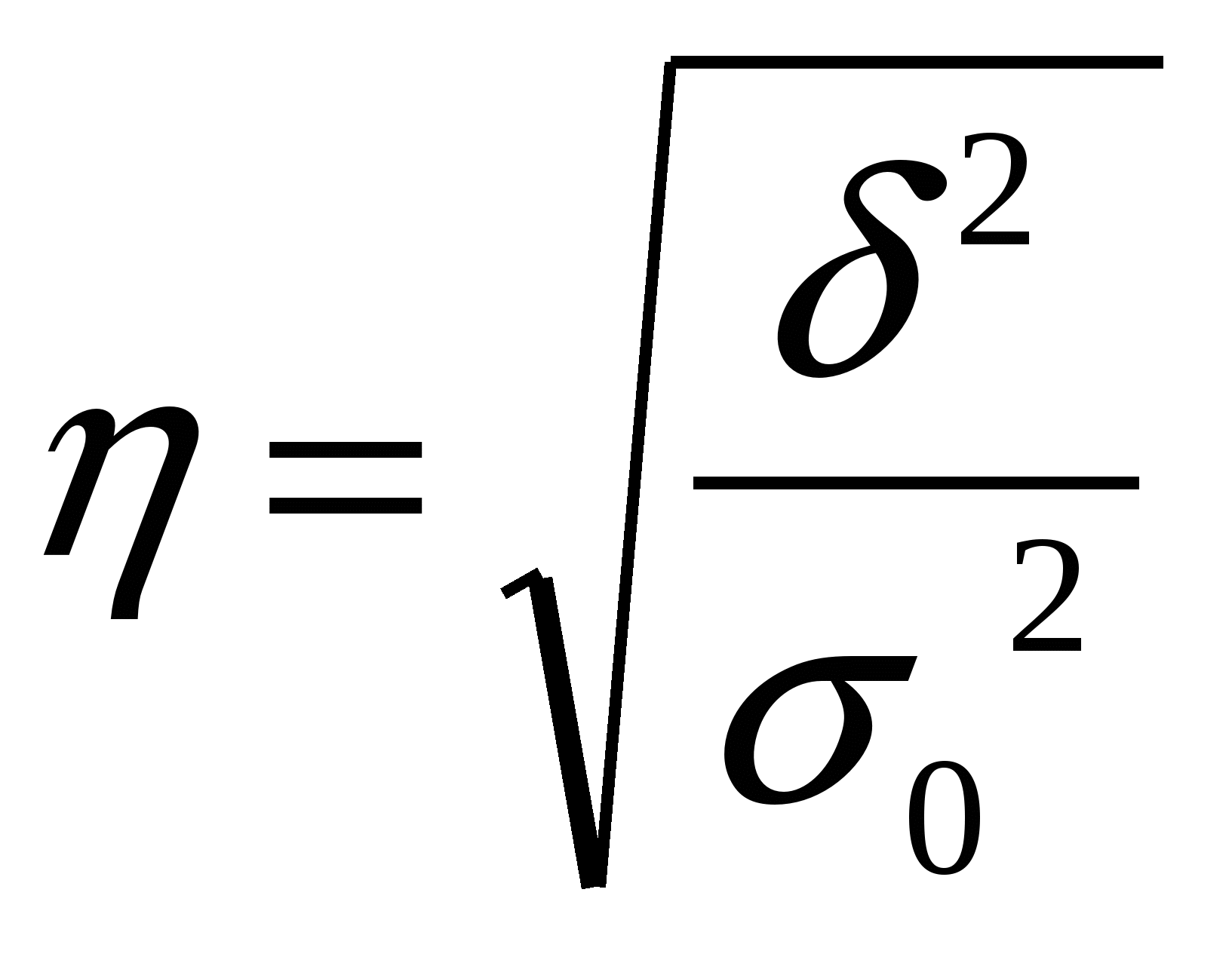 , , Показатель асимметрииСредняя квадратическая ошибка: Если Показатель эксцесса (островершинности)Средняя квадратическая ошибка: Кривые распределенияКривая линия, которая отражает закономерность изменения частот в чистом, исключающем влияние случайных факторов виде, называется кривой распределения. Плотность распределения (расчет теоретических частот) Критерий согласия К. Пирсона (для проверки близости теоретического и эмпирического распределений, для проверки соответствия эмпирического распределения закону нормального распределения) Критерий согласия Романовского Если к<3, то можно принять гипотезу о нормальном характере эмпирического распределения Критерий Колмогорова Распределение Пуассона (теоретические частоты) Выборочное наблюдениеN – объем генеральной совокупности n – объем выборочной совокупности (число единиц, попавших в выборку) р – генеральная доля (доля единиц, обладающих данным признаком в генеральной совокупности) w – выборочная доля S – среднее квадратическое отклонение признака в выборочной совокупности. Неравенство Чебышеба При неограниченном числе наблюдений, независящих друг от друга из генеральной совокупности с вероятностью сколь угодно близкой к 1, можно утверждать, что расхождение между выборочной и генеральной средней будет сколь угодно малой величиной Теорема Ляпунова Дает количественную оценку ошибки. При неограниченном объеме из генеральной совокупности с Р расхождения выборочной и генеральной средней равна интегралу Лапласа 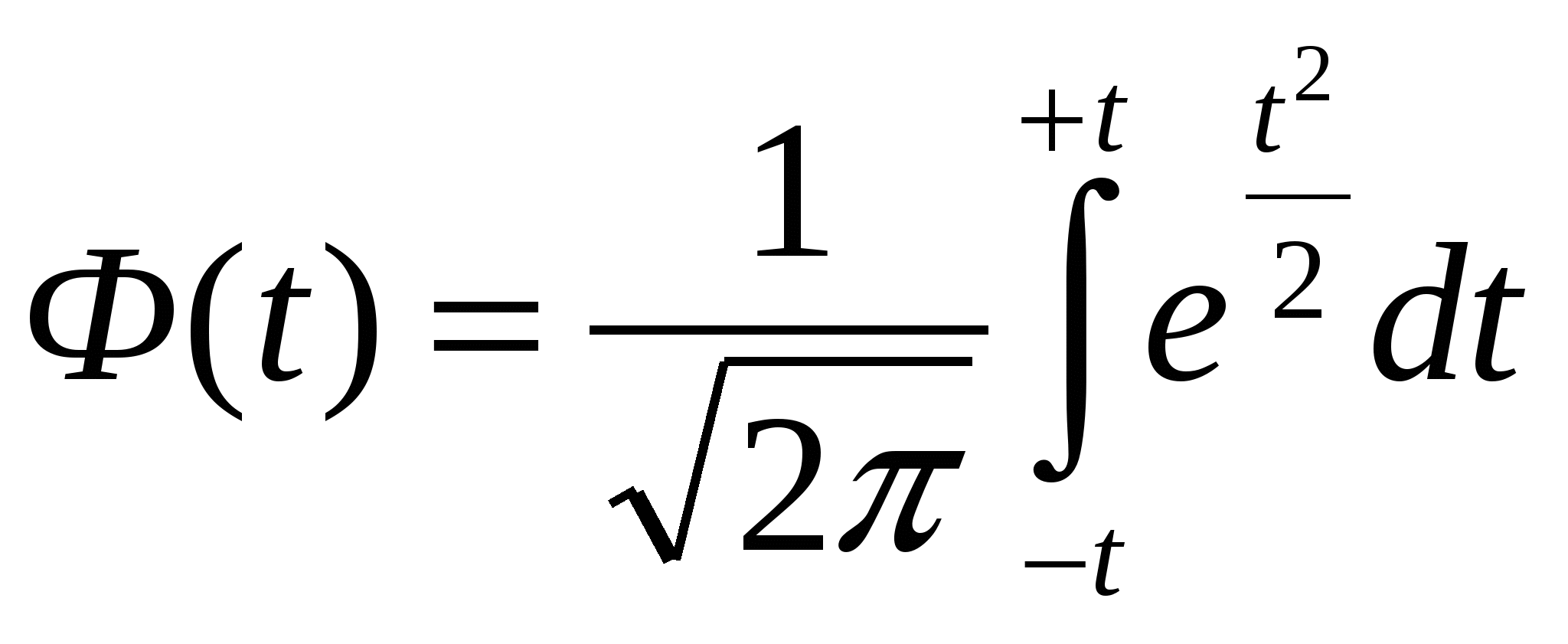 - нормированная функция Лапласа (интеграл Лапласа) - нормированная функция Лапласа (интеграл Лапласа)Р – гарантированная вероятность t – коэффициент доверия, зависящий от Р
Средняя ошибка (n>30) при случайной повторной выборке: При случайной бесповторной выборке: Формулы ошибок простой случайной выборки
Доверительные интервалы для генеральной средней – Доверительные интервалы для генеральной доли – Доверительная вероятность – функция от t, вероятность находится по приложению3 Формулы для определения численности простой и случайной выборки
Типичная выборкаПрименяется в тех случаях, когда из генеральной совокупности можно выделить однокачественные группы единиц (или однородные), затем из каждой группы случайно отобрать определенное число единиц в выборку. Стандартная среднеквадратическая ошибка: Повторный отбор - 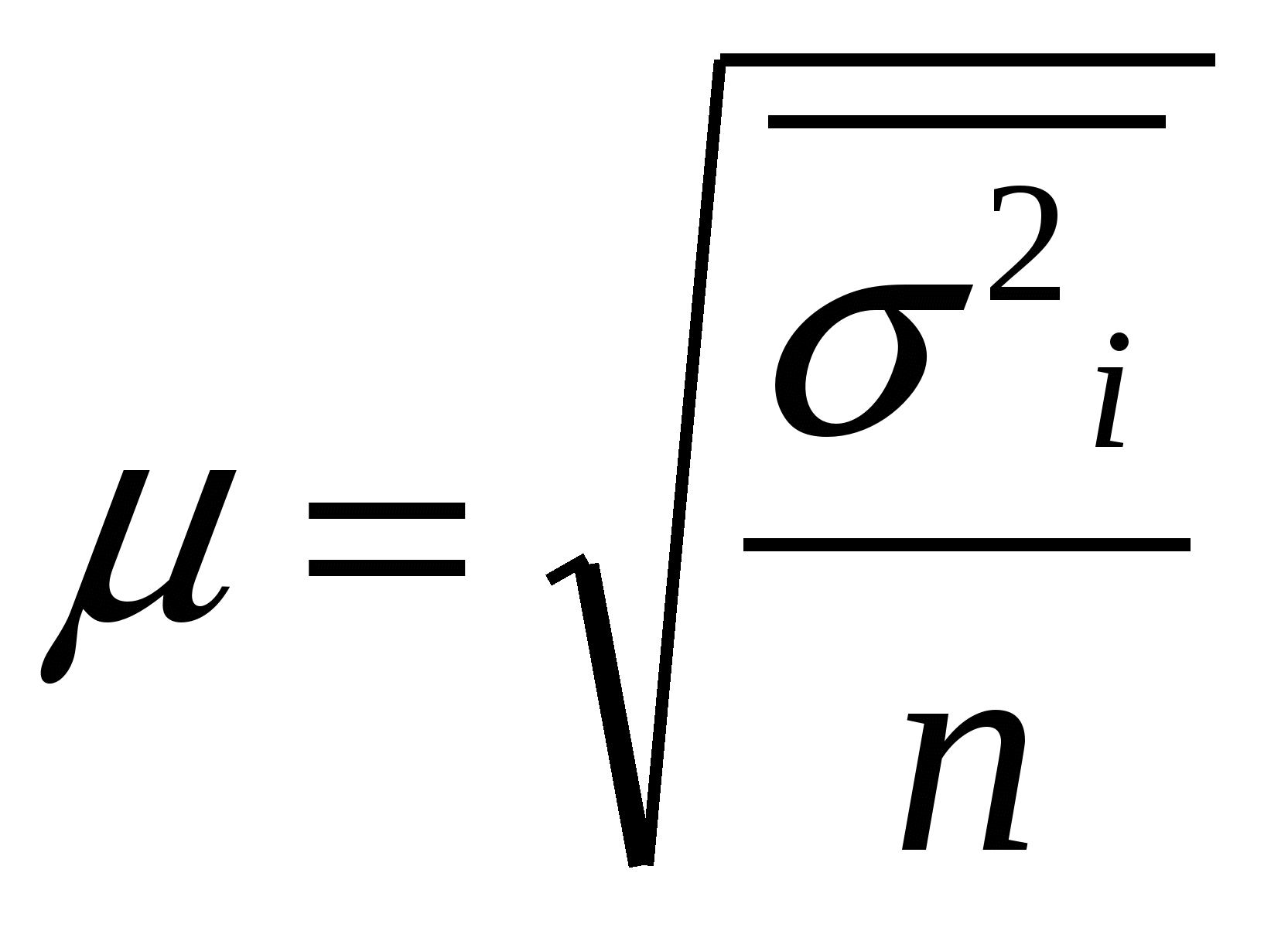 , , Бесповторный отбор - 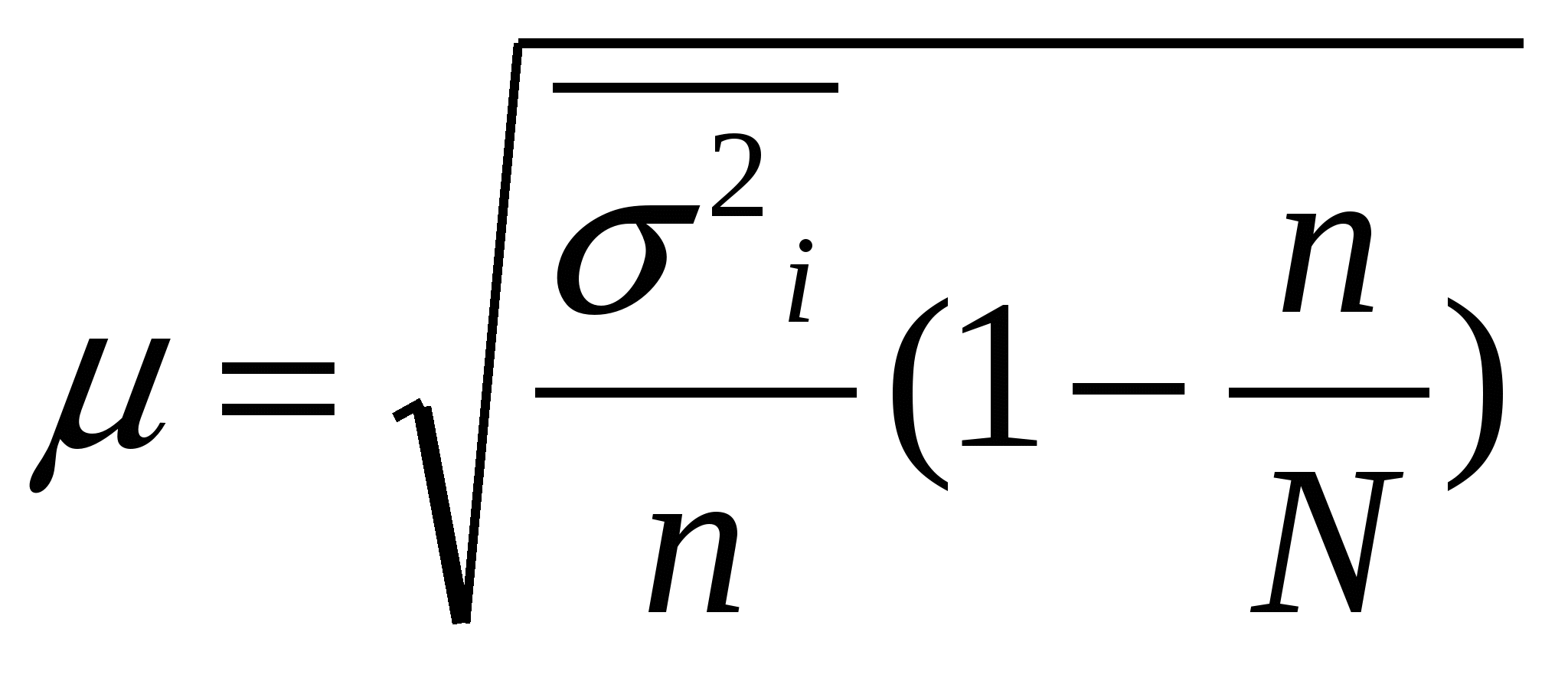 Отбор единиц при типичной выборке из каждой типичной группы: 1.Равное число единиц 2.Пропорциональный отбор 3.Отбор единиц с учетом вариации случайного признака Серийная выборкаВместо случайного отбора единиц совокупности осуществляется отбор групп (серий, гнезд). Внутри отобранных серий производится сплошное наблюдение. Средняя стандартная ошибка: Повторный отбор - 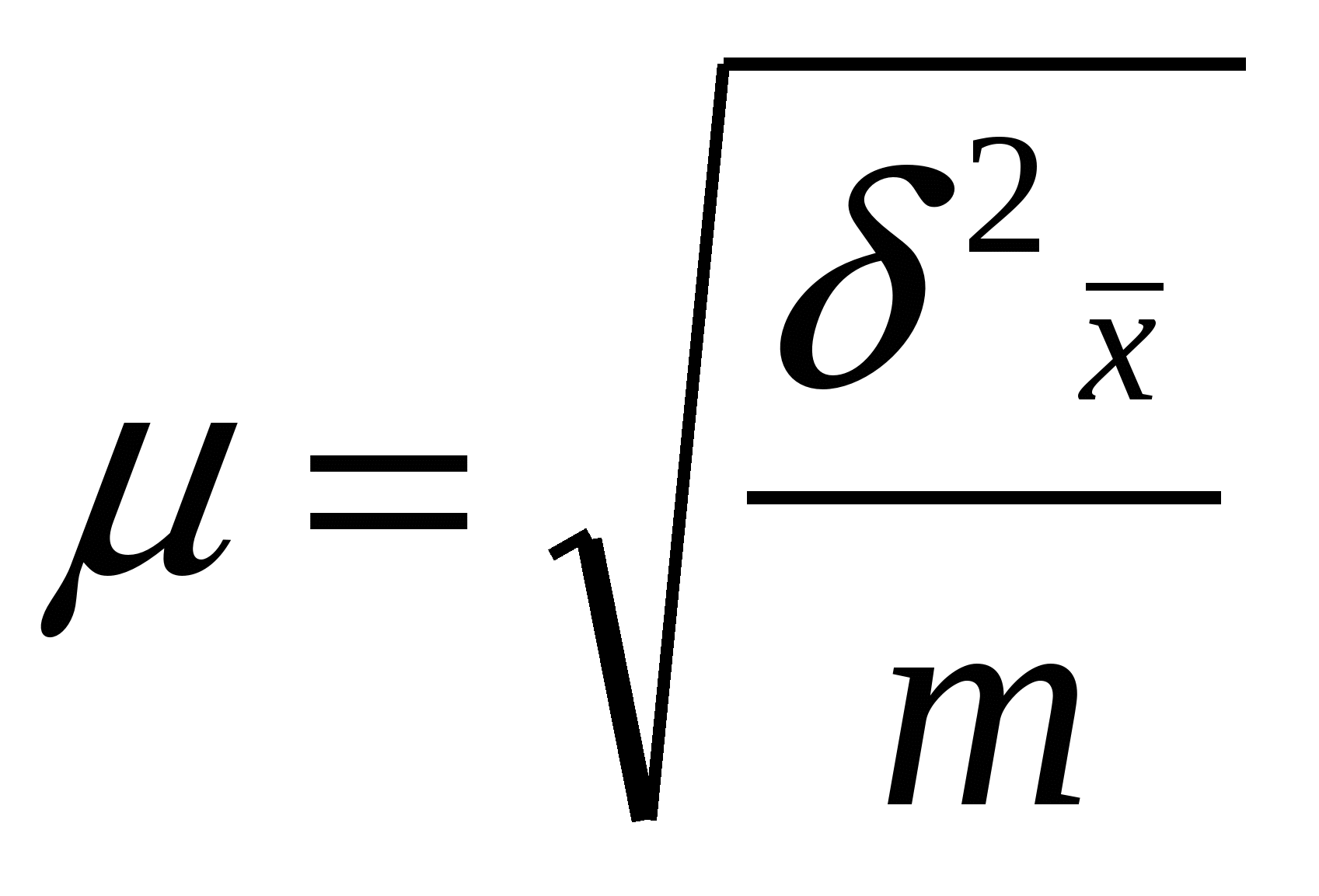 , , Бесповторный отбор - 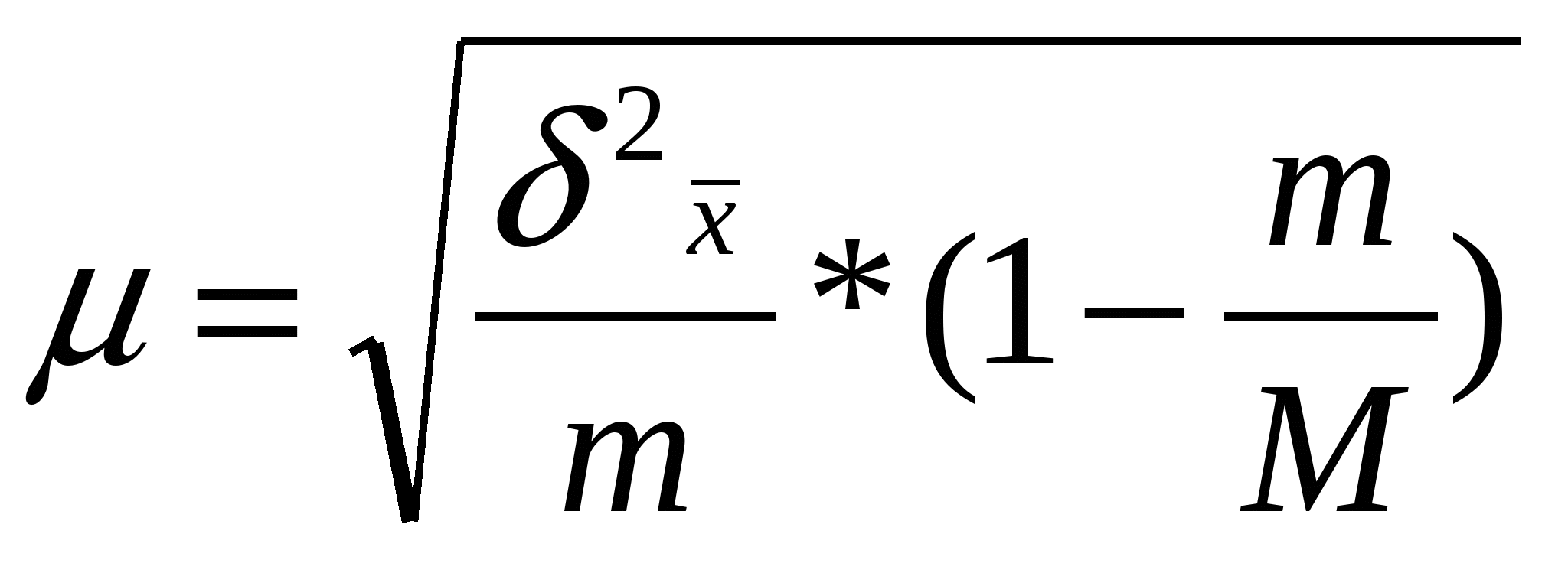 , M – общее число серий , M – общее число серийМалые выборкиВыборки, при которых наблюдением охватывается небольшое число единиц (n<30) Средняя ошибка малой выборки Вероятность того, что генеральная средняя находится в определенных границах, определяется по формуле Корреляционная связьДля оценки однородности совокупности – коэффициент вариации по факторным признакам Линейный коэффициент корреляции Несгруппированные данные Сгруппированные данные - Оценка существенности линейного коэффициента корреляции при большом объеме выборки при недостаточно большом объеме выборки Корреляционное отношение 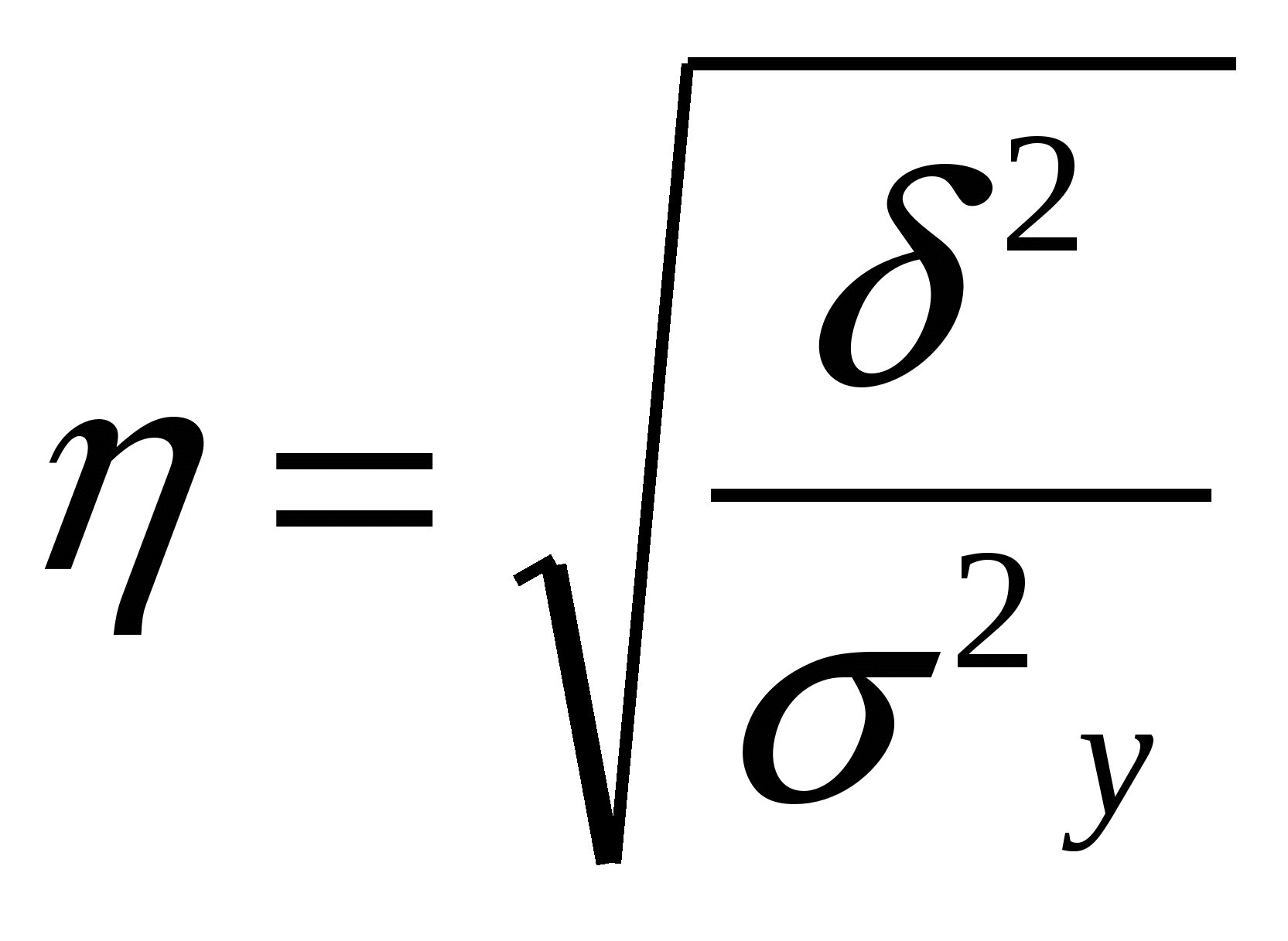 , , 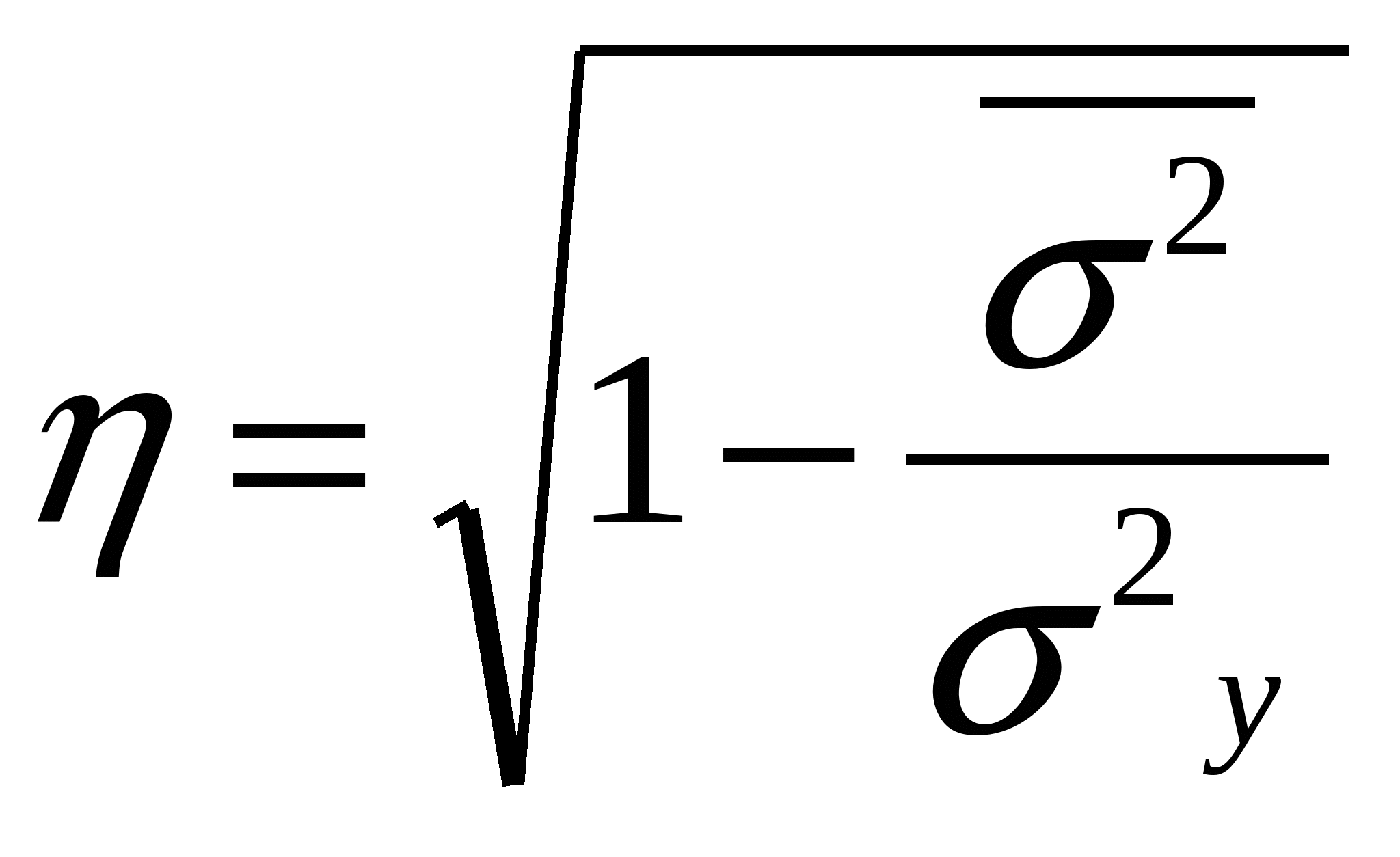 , где , где 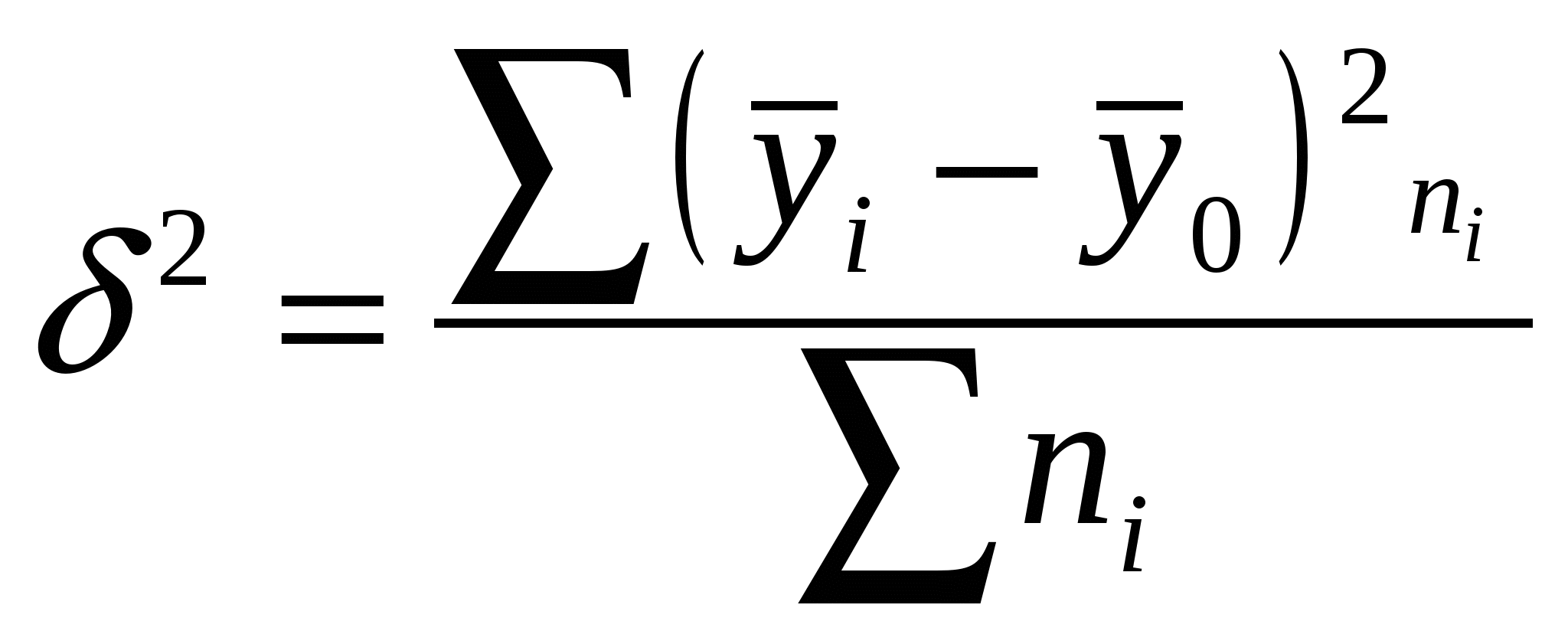 , , 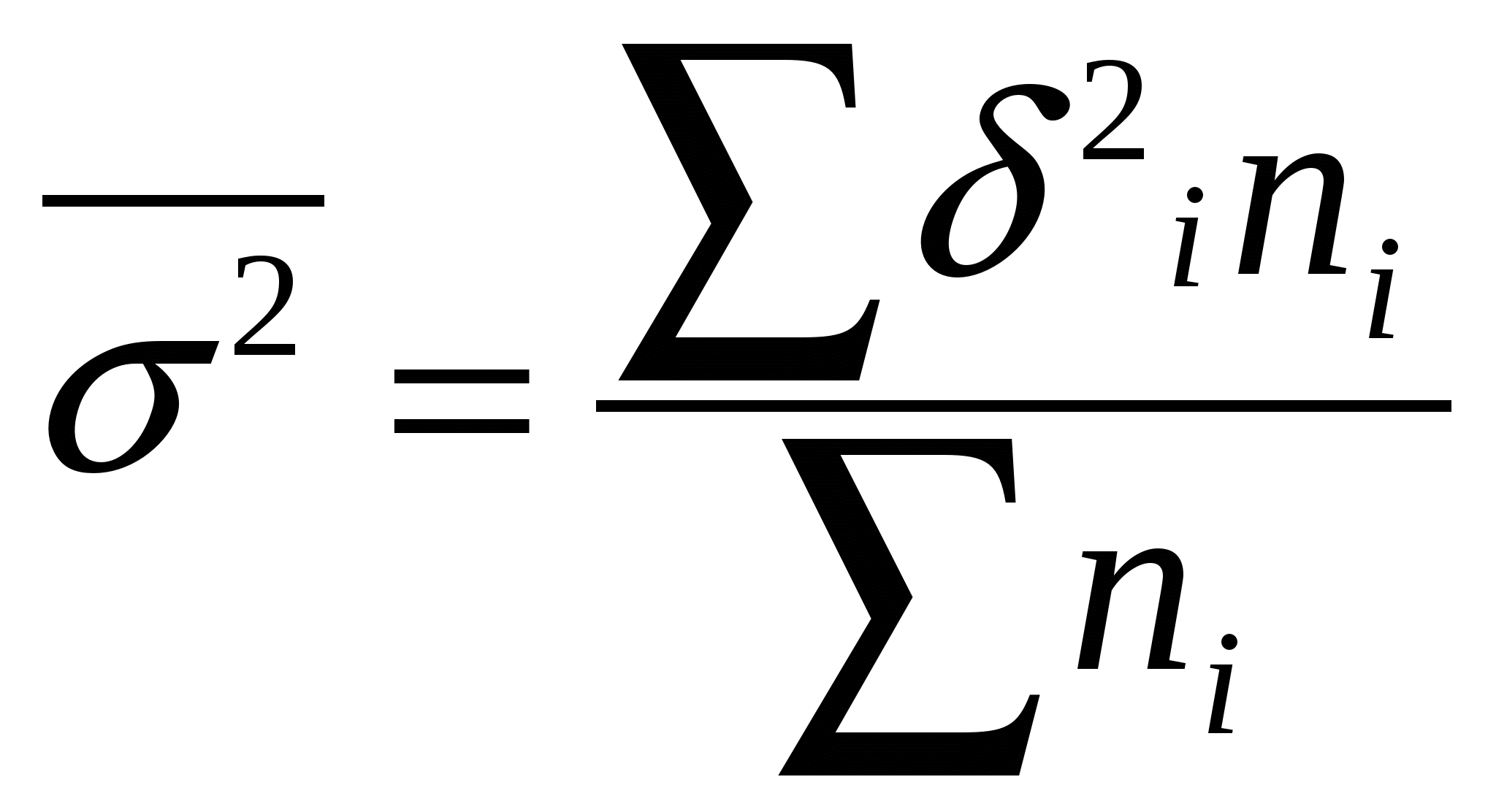
Коэффициент ассоциации Коэффициент контингенции Уравнение регрессииЛинейная Гиперболичская Параболическая Показательная Для проверки возможности использования линейной функции определяется разность Достоверность уравнения корреляционной зависимости Если это отношение не превышает 10-15%, то уравнение хорошо отображает изучаемую взаимосвязь. Ряды динамикиПоказатели динамики
Средние показатели динамики
ТрендыЛинейный Пусть Семестр 2 (Индексы)Индекс – относительная величина, характеризующая изменение уровней сложных социально-экономических показателей во времени, в пространстве или по сравнению с планом. Индивидуальный индекс физического объема выпуска продукции Индивидуальный индекс цен Индивидуальный индекс затрат на выпуск продукции Индивидуальный индекс стоимости продукции Агрегатный индекс физического объема продукции (Относительное изменение физического объема продукции в отчетном периоде по сравнению с базисным) Средний взвешенный арифметический индекс физического объема продукции Средний взвешенный гармонический индекс физического объема продукции 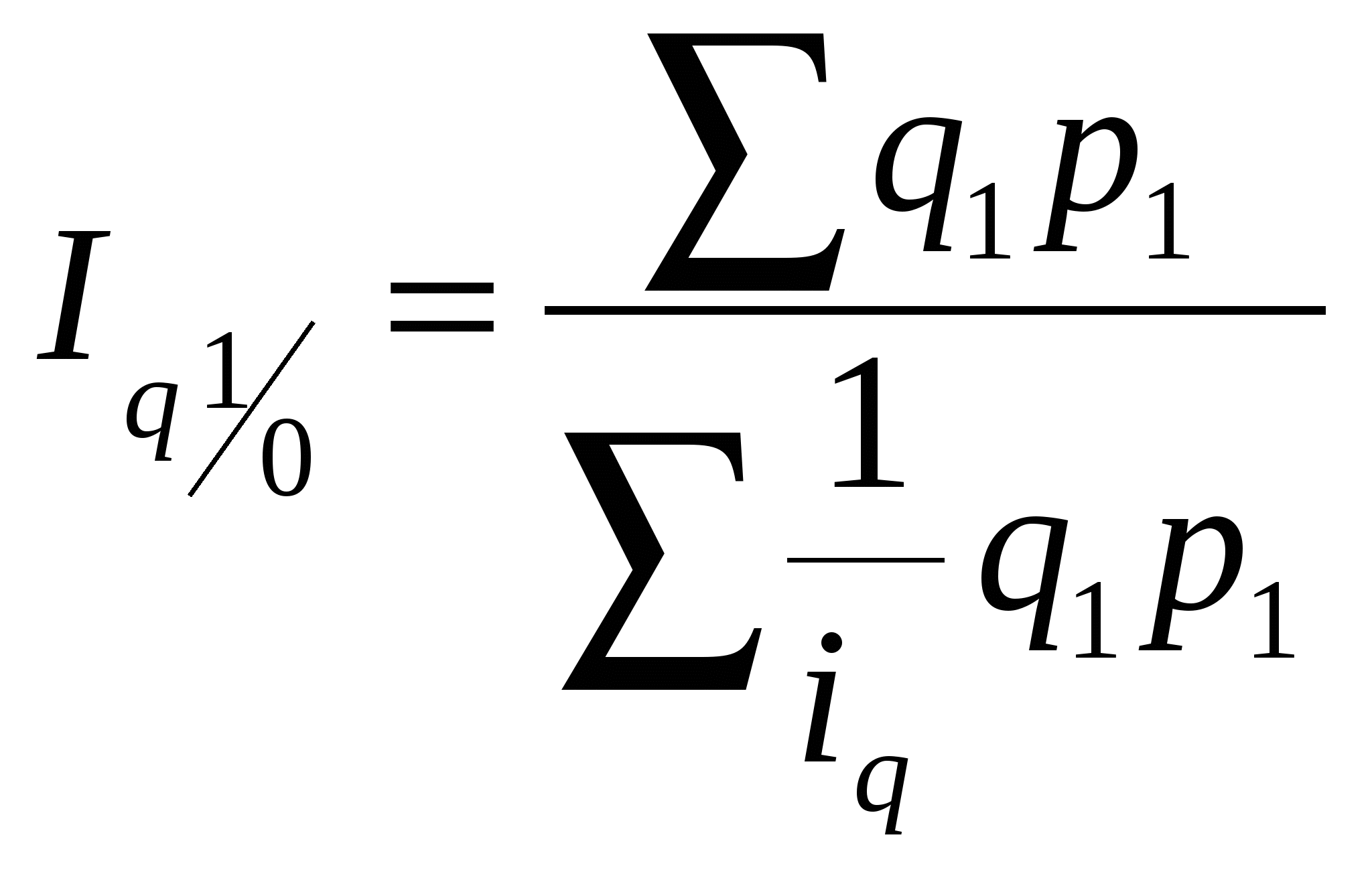 Агрегатный индекс цен (характеризует среднее изменение цен по совокупности различных видов продукции) Агрегатный индекс цен (характеризует среднее изменение цен на потребительские товары) Агрегатный индекс затрат на выпуск всей продукции Двухфакторный индекс Связь: Индекс планового задания Индекс степени выполнения плана Связь: Изменение себестоимости продукта А по фирме Индекс влияния структурных сдвигов в объеме продукции Абсолютное изменение общей стоимости продукции за счет двух факторов: Абсолютное изменение общих затрат на выпуск продукции за счет двух факторов: Выработка - W = Q/T , W – выработка, Q – физический объем реализованной продукции/услуг, T – затраты живого труда (среднесписочная численность работников/рабочих) Трудоемкость (показатель, обратный выработке) - t = 1/W = T/Q Трудоемкость характеризует величину затрат рабочего времени на единицу произведенной продукции. Индекс динамики выработки переменного состава, определяющий отношение выработки отчетного периода к выработке базисного периода - Iw = W1/W0 Этот индекс характеризует изменение производительности труда под влиянием всех факторов, а именно: НТП, человеческого фактора (квалификация и т.п.) и др. Индекс динамики трудоемкости - It = t1/t0 Индекс динамики трудоёмкости характеризует изменение трудоёмкости в отчетном периоде по сравнению с базисным, и его величина зависит от изменения трудоёмкости производимой продукции и от изменения объемов производства этой продукции. IQ = IW * IT – система связанных индексов, которая позволяет определить влияние интенсивных и экстенсивных факторов на изменение объема продукции, услуг. Среднегодовая стоимость основных фондов в базисном и отчетном годах - Фондоотдача - Фондоёмкость – показатель, обратный фондоотдаче, за базисный и отчетный годы по формуле Индекс динамики фондоотдачи IVп.с.= Индекс динамики фондоемкости Влияние интенсивного (качественного) и экстенсивного (количественного) факторов на абсолютное изменение физического объема продукции/услуг. Под экстенсивным фактором обычно понимают абсолютное изменение основных фондов. Под интенсивным – абсолютное изменение показателя фондоотдачи. Влияние экстенсивного фактора: Влияние интенсивного фактора: Влияние обоих факторов: Показатели фондовооруженности рабочих Индекс динамики фондовооруженности: Коэффициент износа основных фондов на конец отчетного года Износ фондов на конец отчетного года | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||