северозападный государственный заочный технический университет
 Скачать 0.88 Mb.
|
|
1. a 0 0; 5. 2. a1 a; 6. 3. a a a; 7. a 0 a; a1 1; a a a; 4. a a 0; 8. a a 1;  9. a a.В заключение необходимо подчеркнуть, что в алгебре логики нет степеней и коэффициентов. Кроме того, умножение на 1 или прибавление 0 не изменяет выражения. Таблицы истинности и переключательные функции При помощи таблиц истинности (ТИ) либо задаются законы функционирования разрабатываемых схем, либо анализируются принципы работы уже существующих схем. В таблице истинности указываются (табл.1.2.1): номера кодовых комбинаций (наборов) (n), которые могут поступить на вход рассматриваемой схемы; сами кодовые комбинации с обозначением соответствующих двоичных разрядов через символы "a","b","c" (или через xс добавлением номера аргумента); выходной сигнал y, который должен образоваться на выходе схемы в соответствии с заданным алгоритмом работы схемы в результате поступления на ее вход той или иной кодовой комбинации. Таблица 1.2.1.
Пример 1.2.1. На вход разрабатываемой схемы могут поступать кодовые комбинации в двоичной системе счисления разрядностью три бит каждая. Разработать схему, которая бы вырабатывала на выходе логическую единицу в случае поступления на вход схемы кодовых комбинаций с нечетным числом единиц. В табл. 1.2.1 в области кодовых дорожек указаны 8 кодовых комбинаций, которые в принципе могут поступить на вход схемы при трехбитовых кодовых комбинациях. В области выходного сигнала проставлены единицы против тех кодовых комбинаций, которые имеют нечетное число единиц. Логику работы схемы, заданной в виде таблицы истинности, возможно перевести в математическую форму. С этой целью по таблице истинности составляется переключательная функция (ПФ), в которой используются функции алгебры логики. Переключательная функция должна содержать все входящие кодовые комбинации, соединенные логической функцией ИЛИ. Такая форма записи называется совершеннойдизъюнктивнойнормальнойформой(СДНФ). Это указывает на то, что на вход может поступить или эта кодовая комбинация, или эта, или эта, или …. Аргументы, входящие в кодовые комбинации в виде логической единицы, в переключательной функции указываются в прямом коде. Аргументы, входящие в переключательную функцию в виде логического нуля, указываются в переключательной функции в обратном коде. Такая запись получила название - Совершенная Дизъюнктивная Нормальная Форма (СДНФ). Пример 1.2.2. По таблице истинности предыдущего примера (табл. 1.2.1) составить переключательную функцию в теоретическом базисе Буля. Переключательная функция указывает, какие кодовые комбинации, поступающие на вход схемы, вызывают появление логической единицы на выходе этой схемы: y a b c a b c a b c a b c . Минимизация переключательных функций Работа любого дискретного автомата полностью описывается переключательной функцией. При физической реализации данных переключательных функций приходится обращать внимание на общее количество используемых в ней логических элементов и стремиться к уменьшению их количества при сохранении логики работы разрабатываемой схемы. Для этого необходимо уметь отыскивать минимальные, наиболее экономичные формы записи переключательных функций. Для этих целей используются методы непосредственных преобразований и методы минимизации с помощью карт Карно. Метод непосредственных преобразований сводится к минимизации исходной переключательной функции путем преобразования отдельных ее членов и частей в соответствии с законами и аксиомами алгебры логики.        n=2; (a, b) n=3; (a, b, c)   n=4; (a, b, c, d) n=5; (a, b, c, d, e)Рис. 1.2.2. н у ю  Наиболее действен ым методом минимизации является метод карт Карно. Карты Карно использ ют для минимизации перекл чательных функций, р  содержащих не более 7 аргументов. На рис. 1.2.2 показаны числа аргументов (от 2 до 5). При использовании карт Ка карты для различного но переключательную функцию выражают в базисе Буля. Карты Карно позволяют производить основную —  операцию минимизации операцию склеивания для нескольких аргументов. л Карта Карно представляет собой поле, разделенное количеству кодовых комбинаций в минимизируемой перек на 2nклеток, равное ючательной функции. сверху карты и тогда относятся ко всему столбцу или стро квадратов (рис. 1.2.3). е следующих за ними   Рис. 1.2.3. Пример заполнения карты Карно. Каждая клетка отличается от соседней значением одного аргумента. Такое расположение наборов дает возможность производить операцию склеивания в соседних клетках. к Например, для пере лючательной функции y a b c a b c2  карта Карно будет иметь вид, представленный на рис. 1. .4. Обычно на картах Карно инверсии аргументов не указываются. В тех клетках, которые соответствуют кодовой комбинации переключательной функции, ставится единица. Обе единицы можно обвести единым контуром. Заметим, что полученный контур полностью   лежит в области прямых значений aи bи сечется границей прямого и инверсного значения аргумента с. Рис.1.2.4. Правила выделения группы  Из сказанного можно сделать вывод, что в контур входят прямые значенияаргументов аи bи как прямое, так и инверсное значения аргумента с.Поэтому л минимизированная перек ючательная функция будет иметь вид: y a b.Правила минимизации. Минимизации подлежат переключательные функции, Буля. выраженные в базисе Для каждой входной кодовой комбинации переключательной функции в карте Карно находится соответствующая клетка и там проставляется единица. Соседние клетки с единицами охватываются контуром (рис.1.2.5). Контур может быть либо квадратной, либо прямоугольной формы. Возможна частичная накладка одного контура на другой. Верхние и нижние крайние клетки карты рассматриваются как рядом лежащие. Каждый контур должен содержать четное число клеток по каждой стороне (в соответствии с закономерностью – 2n). Возможен контур, состоящий из одной клетки. Количество контуров должно быть минимальным. Каждый контур должен охватывать максимальное количество клеток. Минимизированная переключательная функция составляется как логическая сумма кодовых комбинаций. Каждая кодовая комбинация характеризует один контур и входящие в него аргументы в прямом или инверсном значениях. В кодовую комбинацию, составленную по контуру, не входят аргументы, присутствующие в контуре в прямом и инверсном значении одновременно. 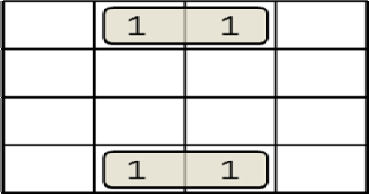 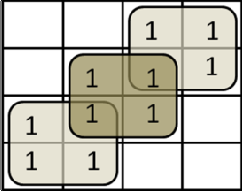 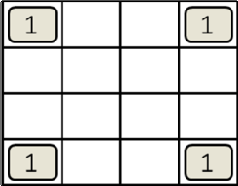 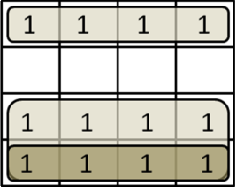 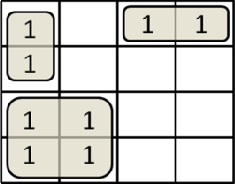 Рис. 1.2.5. Работа с группами Пример 1.2.3. Дана переключательная функция вида y a b c a b c a b c a b c a b c a b c. Карта Карно для данной переключательной функции представлена на рис. 1.2.6. 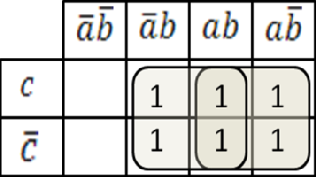 Если все единицы Рис. 1.2.6 объединить в два контура, то минимизированная переключательная функция будет иметь вид y b a. Составление функционально-логической схемы в базисе Буля Функционально-логическая схема (ФЛС) характеризует не электрические, а логические связи между элементами, каждый из которых соответствует той или иной функции базиса Буля. Пример 1.2.4. Дана переключательная функция вида Y a b c a b c a b c a b c. В этой переключательной функции имеется 4 логических элемента И a b c; a b c; a b c; a b c; и один элемент ИЛИ, объединяющий выходы всех элементов И. На входах схемы должны быть установлены инверторы, позволяющие иметь внутри схемы значения аргументов, противоположные их входным значениям. Схема будет иметь вид, как это указано на рис. 1.2.7.  Рис. 1.2.7. Произведем минимизацию функции. Карта Карно для минимизации данной переключательной функции дана на рис. 1.2.8. Карта содержит три контура. Минимизированная переключательная функция примет вид Y a c b c a b. 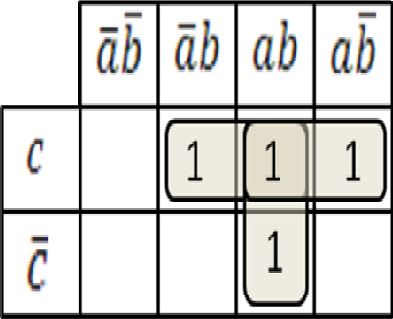 Рис. 1.2.8.  По минимизированной переключательной функции строится функционально- логическая схема (рис. 1.2.9). Рис. 1.2.9. Вопросы для самопроверки по теме 1.2 Перечислите три основные функции составляющие базис Буля. Какова отличительная особенность инверсии? Чем отличаются УГО конъюнкции и дизъюнкции? Используя аксиомы алгебры Буля, докажите основные законы? В чем заключается принципиальное отличие арифметического и логического сложений? Какие данные записываются в таблицу истинности? Что такое совершенная дизъюнктивная нормальная форма записи функции? В чем заключается процесс минимизации функции? Что из себя представляет карта Карно? 10.Каковы правила выделения групп в карте Карно? 11.По каким правилам выполняется минимизация внутри группы? 12.Что опреднляет функционально-логическая схема? Промышленный базис Переход в промышленный базис Логические схемы И и ИЛИ создаются из пассивных элементов: диодов, резисторов, конденсаторов и т. д. При прохождении через них электрический сигнал часть своей энергии тратит на нагрев этих элементов и теряет свою форму и уменьшается по амплитуде. Для восстановления амплитуды и формы сигнала на выходе этих логических схем устанавливаются однокаскадные транзисторные усилители, работающие в режиме насыщения. С точки зрения логики однокаскадный усилитель является инвертором. В результате этого получаются сложные логические элементы типа И-НЕ и ИЛИ-НЕ, образующие промышленный базис (ПБ). Промышленность выпускает только схемы И-НЕ и ИЛИ-НЕ, из которых возможно собрать физически реальную фунционально-логическую схему. Элемент ИЛИ-НЕ называется элементом Пирса и математически обозначается |
