северозападный государственный заочный технический университет

• Название: северозападный государственный заочный технический университет
• Дата: 03.11.2021
• Размер: 0.88 Mb.
• Имя файла: met_97_Shemotehnika-sistem-upravleniya-ASU-SZTU-metodichka-2010..docx
• Тип: Документы; #262689
• страница: 10 из 14

3. Синтез дискретных автоматов с памятью.

В разделе представлено 3 темы:

• 
  определение дискретного автомата с памятью;
  
• 
  способы задания дискретных автоматов с памятью;
  
• 
  табличный способ задания дискретного автомата с памятью;
  

На основе теоретического материала выполняется лабораторная работа №3:

• 
  синтез дискретных автоматов с памятью.
  

По результатам изучения раздела: выполняется тест; защищаются лабораторные работы; студенты заочной и очно-заочной форм обучения выполняют задания контрольной работы.

1. 
   Определение дискретного автомата с памятью
   

Любую схему вычислительной техники можно условно представить как совокупность операционных устройств и устройства управления. К операционным устройствам относятся устройства памяти, регистры, сумматоры, шифраторы и дешифраторы, которые производят суммирование сигналов, запоминание, сдвиг, инвертирование и т. д. К устройствам управления относятся устройства, которые, координируя всю работу операционных устройств, определяют последовательность переработки исходной информации.

Задача разработки операционных устройств, вследствие их регулярности и однотипности, в настоящее время в основном решена. Отечественной промышленностью серийно выпускаются различные устройства, призванные реализовать функции, которые в той или иной мере возлагаются на операционные устройства. Совершенно иначе обстоит дело с устройствами управления. Каждая схема вычислительной техники строится по логике работы присущей только ей, скорости обработки информации, характеру и последовательности обработки входных и выходных сигналов, видам коррекции и т. д. Поэтому разработка

устройств управления представляет собой наиболее сложную задачу, от успешного решения которой в значительной степени зависит качество системы управления.

Как операционные устройства, так и устройства управления состоят из элементов, реализующих элементарные логические функции, и различного рода запоминающих элементов. Наличие в схеме запоминающего элемента значительно расширяет ее логические возможности. Но наличие в схеме запоминающего элемента приводит к тому, что выходной сигнал устройства зависит не только от вида входного сигнала, но и от состояния устройства, которое оно приобрело в результате переработки информации от предыдущего входного сигнала.

Математической моделью, соответствующей формальному представлению функционирования дискретного устройства с элементами памяти, является дискретныйавтоматспамятью.

Дискретные автоматы с памятью отличаются от дискретных автоматов без памяти тем, что выходной сигнал дискретного автомата с памятью зависит не только от входного сигнала, поступившего в автомат в данный момент времени, но и от входных сигналов, поступивших в автомат в предыдущие моменты времени, а также определяет его состояние в последующие моменты времени.

Математически дискретные автоматы с памятью задаются пятью конечными множествами:

• 
  множеством возможных входных сигналов Х (х1, х2, ,ХN);
  
• 
  множеством возможных выходных сигналов Y (y1, y2, ,yN);
  
• 
  множеством возможных внутренних состояний дискретного автомата с памятью А (а1, а2, ,аN);
  
• 
  функцией переходов δ, реализующей отображение множеств А и X в Y;
  
• 
  функцией выходов λ, реализующей отображение множеств А и X в Y.
  

Процесс функционирования дискретного автомата с памятью заключается в том, что при подаче на его вход некоторой последовательности входных сигналов он

переходит из одного состояния в другое и формирует последовательность выходных сигналов.

Всю совокупность информации, поступившую как на вход, так и с выхода автомата, кодируют конечной совокупностью символов. Эта совокупность называется алфавитом, отдельные символы, образующие алфавит, — буквами, а любые конечные упорядоченные последовательности букв данного алфавита — словами. Функционирование автомата всегда рассматривается в дискретные моменты времени, которые называются тактовыми моментами. Предполагается, что поведение автомата не зависит от интервала времени между тактами. Поэтому фактически переменной величиной является не само время, а порядковые номера тактовых моментов.

В зависимости от положения элемента памяти в структурной схеме автомата последние классифицируются на две большие группы. К первой группе дискретных автоматов с памятью относятся автоматы, в которых выходной сигнал одновременно зависит как от состояния автомата (памяти), так и от значения входного сигнала, действующего на автомат в данный момент времени. Автоматы первой группы называются автоматами Мили. Ко второй группе дискретных автоматов с памятью относятся автоматы, в которых выходной сигнал зависит лишь от внутреннего состояния автомата (памяти), определяемого входным сигналом в предыдущий тактовый момент времени. Автоматы второй группы называются автоматами Мура.

Вопросы для самопроверки по теме 3.1

1. 
   Что такое дискретный автомат с памятью?
   
2. 
   В чем отличие дискретного автомата с памятью от автомата без памяти?
   
3. 
   Какова природа дискретности автомата?
   
4. 
   Каково принципиальное отличие автомата Мура от автомата Мили?
   

2. 
   Способы задания дискретных автоматов с памятью
   

Основными задачами теории дискретных автоматов являются задачи анализаи синтеза. Под анализом дискретного автомата подразумевается определение закона его функционирования по уже разработанной конкретной функционально- логической схеме. Синтез дискретных автоматов с памятью заключается в построении функционально-логической схемы автомата по заданному закону функционирования. При решении задачи синтеза, ведущей к созданию функционально-логической схемы автомата, обычно выделяют два этапа, включающие абстрактный и структурный синтезы. На этапе абстрактного синтеза по закону функционирования дискретного автомата создается его математическая модель. При этом не принимается во внимание физическая реализация схемного решения. На этапе структурного синтеза рассматриваются вопросы кодирования и выражения математической модели реально существующими логическими элементами выбранного или заданного базиса с последующим построением функционально-логической схемы автомата.

Для решения задачи абстрактного синтеза, прежде всего необходимо описать условия функционирования дискретного автомата с памятью на некотором формальном языке, который явится стандартной и формализованной формой задания автомата. При синтезе дискретных автоматов без памяти задание закона функционирования достигалось при помощи таблиц истинности и переключательных функций, которые однозначно определяли значения выходных сигналов при поступлении на автомат всех возможных комбинаций входных сигналов. Но для дискретных автоматов с памятью такое задание закона функционирования не пригодно, так как оно не отображает внутреннего состояния автомата. Чтобы задать дискретный автомат с памятью, необходимо описать все элементы множеств (X; Y; A; δ; λ), т. е. входной и выходной алфавиты, алфавит состояний, а также функции переходов и выходов. Существует несколько способов задания работы дискретных автоматов с памятью, наибольшее распространение из которых получили табличный, графический и способ граф-схем алгоритмов.


й
Табличный и графически способы задания дискретных автоматов с памятью часто

объединяют одним названием — канонический способ.

Для общего случая структура некоторого дискретного автомата с памятью

представлена на рис. 3.2.1. На вход автомата поступает совокупность (множество)


м
входных сигналов X(x₁,х₂,…,х_m),и на выходе фор ируется совокупность


и
(множество) выходных с гналов Y(у_иу₂,…, у_п),отображающих как совокупность


а
входных сигналов в данный момент времени, так и совокупность внутренних состояний дискретного автомата A(a₁,a₂,…,a_k). Для упрощения абстрактного

у
синтеза разделим структ

рную схему дискретного автомат

на две части: КЭ—

комбинационный элемент, представляющий собой в общем случае дискретный автомат без памяти (комбинационная схема), и ЭП— элемент памяти. Элемент памяти автомата состоит из к двоичных (два устойчивых состояния) запоминающих элементов T₁,Т₂,…,Т_к,.Состояния запоминающих элементов отображаются

сигналами A (а₁ a2,

устойчивого состояния

…, a_k). Переход запоминающих в другое происходит под в

элементов из одного здействием сигналов

k

о
возбуждения Z(z₁,z₂,…,z).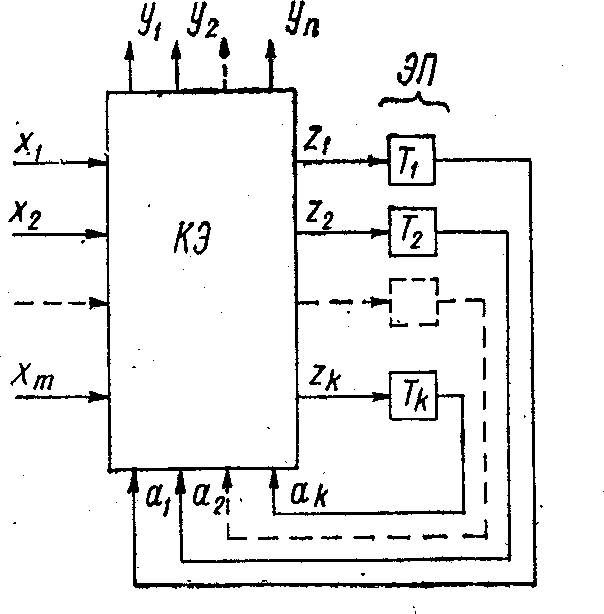

Рис. 3.2.1

Автомат функционирует следующим образом. В момен

т
времени t =0 автомат

о
находится в начальном с

стоянии a_i= а₀.При поступлении

в моменты времени t=

1,2, входных сигналов в автомате формируются выходные сигналы Y(y₁,y₂,…,y_m)и сигналы возбуждения Z(z₁,z₂,…,z_n). Под действием сигналов возбуждения автомат

последовательно переходит в различные состояния а_i. Темп функционирования автомата определяется темпом поступления входных сигналов или сигналов синхронизации.

Совокупность правил, описывающих последовательность изменений выходных сигналов автомата в зависимости от последовательности входных сигналов, называется законом функционирования автомата.

Для того чтобы определить закон функционирования автомата, необходимо задать закон изменения функций перехода и выхода в зависимости от входных сигналов и внутреннего состояния автомата.
Вопросы для самопроверки по теме