северозападный государственный заочный технический университет

• Название: северозападный государственный заочный технический университет
• Дата: 03.11.2021
• Размер: 0.88 Mb.
• Имя файла: met_97_Shemotehnika-sistem-upravleniya-ASU-SZTU-metodichka-2010..docx
• Тип: Документы; #262689
• страница: 6 из 14

При задании чисел в двоично-десятичной системе счисления необходимо указывать расположение старшего и младшего разрядов. Данная система счисления используется, как правило, для ввода информации в устройства вычислительной техники.

2. 
   Арифметические операции над числами, выраженными в двоичной системе счисления
   

Все числа, которыми оперирует вычислительная техника, могут иметь две форы записи.

Естественная форма записи с фиксированной запятой

0,125; 361,1; 21,89.

Нормальная форма записи с плавающей запятой

10^-3125; 10^-13611; 10²0,2189.

В двоичной системе счисления старший бит отводится под знак числа:

0-число положительное; 1-число отрицательное.

1. 
   Сложение двух положительных чисел.
   

В нормальной форме сначала уравнивают порядок чисел. Например

10²0,25 + 10³0,75 = (0,025 + 0,75)10³.

После уравнения порядков складывают их мантиссы.

Пример 1.1.1. Сложить числа +5 и +6.

+5 _⇒ 00101

+6	⇒	00110
+11		01011

2. 
   Вычитание одного числа из другого
   

Данную операцию можно представить как сложение двух чисел с разными знаками.

Например,

А – В = +А + (-В).

Отрицательное число перед сложением переводят в дополнительный код.

Прямой код (N) -5 ⇒ 10101.

Обратный код N

Дополнительный код N  1

-5 ⇒ 11010.

11010+1=11011.

Пример 1.1.2. Вычесть число 5 из числа 6.

6 – 5 = +6 + (-5).

Производится перевод прямого кода числа в обратный по схеме N⇒N⇒

N  1.

-5⇒10101⇒11010⇒11010+1⇒11011.

Выполняется операция сложения

+6	⇒	00110
-5	⇒	11011
+1		100001

Так как старший знаковый разряд имеет один бит, то единица в знаковом разряде пропадает.

Пример 1.1.3. Вычесть число 6 из числа 5.

5 – 6 = +5 + (-6).

Производится перевод прямого кода числа в обратный по схеме N⇒N⇒

N  1.

-6⇒10110⇒11001⇒11001+1⇒11010.

Выполняется операция сложения

+5	⇒	00101
-6	⇒	11010
-1		11111

Если сумма получилась отрицательной (в знаковом разряде единица), то вновь применяют преобразование по схеме N⇒N⇒N  1

11111⇒10000⇒10000+1⇒10001

3. 
   Умножение двух чисел.
   

При умножении производятся две операции. Первая операция.

Сложение по модулю два знаковых разрядов. Операция сложения по модулю два имеет вид (символ )

Y = AB^¯ v A^¯B = A ③ B

00=0

01=1

10=1

11=0

Вторая операция.

Перемножение мантисс сомножителей.
Пример 1.1.4. Умножить число +2 на число -3.

Производится операция сложения по модулю два старших разрядов чисел (число 2 положительное, число 3 отрицательное) для определения знака произведения

01=1.

Произведение будет отрицательным. Перемножаются мантиссы

2	⇒	010
3	⇒	011

_

010

010

000

_ 6 00110

Следовательно, с учетом знака произведение равно -6.

4. 
   Деление одного числа на другое
   

Операция деления производится в два этапа.

Первый этап.

Определение знака частного. Второй этап.

Деление делимого на делитель.

Алгоритм деления.

1. 
   Нахождение разности чисел (делимого и делителя). Если делимое отрицательное, то делитель берут положительным и наоборот. После вычитания знаковый разряд разности сдвигается на один бит вправо.
   
2. 
   Если разность отрицательная, то в частное записывается 0, если разность положительная, то в частное записывается 1.
   
3. 
   Вычитание производится столько раз, насколько разрядность делимого больше разрядности делителя и плюс 1.
   

Пример 1.1.5. Разделить +25 на +5.

Перевод десятичных чисел в двоичные:

+25 ⇒ 011001;

+5 ⇒ 000101.

Определение знака частного

00=0.

Частное положительное.

Чтобы иметь возможность прибавлять или отнимать делитель от делимого делитель заранее представляется в виде положительного и отрицательного чисел.

Для этого переводится делитель в дополнительный код по схеме N⇒N⇒N  1

-5⇒1101⇒1010⇒1010+1⇒1011.

Производится операцию деления.

	0	1	1	0	0	1		+5⇒0101 (-5⇒1011)
	1	0	1	1
1	0	0	0	1				1
		0	0	1	0
		1	0	1	1
		1	1	0	1			0
			1	0	1	1
			0	1	0	1
		1	0	0	0	0		1

Результат деления: 0101, что соответствует десятичному числу +5.

Вопросы для самопроверки по теме 1.1

1. 
   Какие значения могут принимать разряды числа в двоичной и десятичной системах счисления?
   
2. 
   Почему двоичная система счисления является позиционной?
   
3. 
   Что представляет собой двоично-десятичная система счисления?
   
4. 
   Как в двоичной системе счисления задается знак числа?
   
5. 
   Какая операция является базовой для двоичной системы счисления и почему?
   

2. 
   Разработка функционально-логических схем
   

1. 
   Функции алгебры логики
   

Вся теория вычислительных систем базируется на теории алгебры логики. Алгебра логики оперирует тремя логическими зависимостями (функциями). Эти три функции образуют функционально теоретически полный базис Буля (шотландский математик Джон Буль заложил основы алгебры логики). При помощи этих трех функций можно решить алгебраические и арифметические задачи любой сложности.

1. 
   Логическое умножение (конъюнкция). На письме обозначается как "И" (“AND”), математически ─ как символы "" или "". Графически логическое умножение обозначается как прямоугольник с несколькими входами и одним выходом и символом  (AND) в верхнем левом углу прямоугольника (рис. 1.2.1 а).
   

Логическое умножение, например, двух аргументов можно представить в следующем виде:

00=0, 01=0, 10=0, 11=1.

2. 
   Логическое сложение (дизъюнкция). Логическое сложение на письме обозначается как "ИЛИ" (“OR”), а математически обозначается символом "". Графически логическое сложение обозначается как прямоугольник с несколькими входами и одним выходом и символом "1" в верхнем левом углу (рис. 1.2.1 б).
   

Логическое сложение, например, двух аргументов можно представить в следующем виде:

00=0, 01=1, 10=1, 11=1.

3. 
   Логическое отрицание (инверсия). На письме логическое отрицание
   

обозначается как "НЕ" (“NOT”), а математически обозначается как штрих над аргументом " a ". Графически логическое отрицание обозначается как

прямоугольник с одним входом и одним выходом. На выходе

устанавливается признак инверсии в виде кружочка (рис. 1.2.1 в).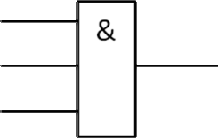

Например, инверсия нуля

а

0 =1 и инверсия единицы 1 =0.




б в

Рис. 1.2.1.

2. 
   
   к
   Основные законы алгебры логи и
   

с
Математические о

новы синтеза дискретных авто

атов базируются на

м

у
законах алгебры логики, главными из которых являются след ющие.

1. 
   Коммутативны
   

закон (переместительный):


й
a b b a;

a b b a.

Результат выполнения операций логического умножения и логического сложения не зависит от того, в каком порядке следуют символы.

2. 
   Ассоциативный закон (сочетательный):
   

(a b


c
(a b) 

Для записи логического опустить.

 c a (b c)  b (a c)  a b c;


)
 a (b c)  b (a c)  a b c.

умножения или логического сложения скобки возможно

3. 
   Дистрибутивный закон (распределительный):
   

• 
  логическое умножение относительно логического сложения
  

a (b c)  a b a c;

• 
  логическое сложение относительно логического умножения
  

(a b)  (a c)  a a b c.

4. 
   Закон инверсии (отрицания), в общем случае известный как закон де Моргана:
   

a b a b;

a b a b_.

В процессе синтеза дискретных автоматов часто приходится упрощать и преобразовывать сложные высказывания. Для упрощения этих преобразований в алгебре логики существует ряд аксиом, основными из которых являются следующие: