северозападный государственный заочный технический университет
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
|
. Рассмотрим пример синтеза дискретного автомата последовательного сложения двух двоичных чисел. Рассматриваемые классы дискретных автоматов называются сумматорами. Сумматоры широко применяются при выполнении различных операций над двоичными числами. Предположим, что необходимо произвести сложение двух чисел (3 и 1), заданных в двоичной системе счисления: 011 и 001. Как известно, процесс сложения двух чисел в двоичной системе счисления происходит следующим образом.
начинается со сложения первых разрядов. В результате сложения первых разрядов в сумме записывается символ 0, а символ 1 переносится в следующий разряд. При выполнении операции сложения в следующем разряде чисел происходит сложение уже не двух символов, а трех: символа 1 первого слагаемого, символа 0 второго слагаемого и символа 1 переноса из предыдущего разряда. В результате выполнения сложения во втором разряде записывается символ 0, а в следующий разряд опять переносится символ 1. При выполнении операции сложения в третьем разряде чисел складываются два символа 0 двух чисел и символ 1, как результат переноса при выполнении операции сложения в предыдущем разряде. Таким образом, на выходе дискретного автомата сигнал, характеризующий сумму двух поданных на вход чисел 011 и 001, последовательно (начиная с младшего разряда) во времени примет значение 0,0 и 1, что в конечном итоге представляет число 4 в двоичном коде (100). Рассматривая общий случай работы дискретного автомата в режиме последовательного сложения двух двоичных чисел, можно показать, что в этом режиме на его вход должны поступать различные сочетания из двух аргументов, а на выходе должен появляться сигнал, который будет характеризоваться входными сигналами и состоянием автомата (т. е. сигналом переноса из предыдущего в последующий разряд). Структурная схема автомата представлена на рис. 3.2.4.  Y Y  Z ZX  A Рис.3.2.4 Табл. 3.2.4
Построим для рассматриваемого дискретного автомата таблицу переходов (табл. 3.2.4). Так как при выполнении операции сложения в предыдущем разряде двух символов единиц в последующий разряд переносится всегда один символ единицы, то в схеме дискретного автомата используется всего одна ячейка запоминающего элемента, характеризующая внутреннее состояние автомата. В табл. 3.2.4 через х1, и х2обозначены входные сигналы, характеризующие символы соответствующих разрядах слагаемых чисел, а через аобозначено внутреннее состояние дискретного автомата. Если считать, что x1 х2и а без инверсий характеризуют символы 1, то по таблице переходов видно, что дискретный автомат переходит в состояние a (0) в том случае, если сумма символов 1, поступивших на его вход и снятых с запоминающего элемента, равна или единице, или нулю. В противном случае дискретный автомат переходит в состояние а (1). Таблица выходов (табл. 3.2.5) характеризует сигнал у на выходе дискретного автомата. В том случае, если сумма символов 1, поступивших на вход дискретного автомата и снятых с запоминающего элемента, равна нечетному числу, то на выходе автомата появится символ 1. В противном случае дискретный автомат выдаст на выходе символ 0. Табл. 3.2.5.
Если рассматриваемый дискретный автомат является тактируемым, т. е. для обеспечения его работы требуются тактовые импульсы С, и в качестве запоминающего элемента используется D-триггер, то для него составляется таблица возбуждения (табл. 3.2.6). Табл. 3.2.6.
Для того, чтобы D-триггер оставался в состоянии a (0) или переходил в состояние a(0), необходимо на его D-вход подавать одновременно с тактовым импульсом С сигнал возбуждения z(0) (первые две строчки таблицы). Для перевода D-триггера в состояние а. (1) необходимо на вход подавать сигнал возбуждения z (1) (две последние строчки таблицы). По таблице выходов составляется функция выхода y x1 x2 a x1 x2 a x1 x2 a x1 x2 a. Данная функция показывает, что на выходе дискретного автомата сигнал будет равен 1 лишь в том случае, если будет реализована одно из четырех перечисленных в функции выхода логических произведений. По таблице возбуждения составляется функция возбуждения z x1 x2 a x1 x2 a x1 x2 a x1 x2 a Данная функция показывает, что запоминающий элемент (D-триггер) будет переходить в состояние а (1) лишь в том случае, если на его D вход одновременно с тактовым импульсом Cбудут поступать сигналы возбуждения z (1), характеризующиеся перечисленными в функции возбуждения логическими произведениями. Для упрощения схемы разрабатываемого автомата произведем минимизацию полученных математических выражений на основе карт Карно. Для функции выходов карта Карно будет иметь вид, представленный на рис. 3.2.5. Как видно из рисунка, функция минимизации не подлежит. 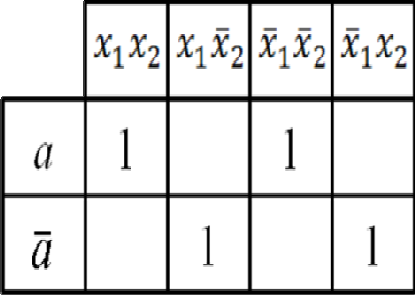 ж Для функции возбу Рис. 3.2.5.  рис. 3.2.6. рис. 3.2.6.Рис. 3.2.6. После охвата единиц контурами минимизированная примет вид: функция возбуждения z x2 a x1 a x1 x2 . Переведем функции выходов и возбуждения в базис Пирса: y x1 x2 a x1 x2 a x1 x2 a x1 x2 a, z x2 a x1 a x1 x2 . На рис. 3.2.7 представлена функционально-логическая схема дискретного автомата последовательного сложения двух двоичных чисел в базисе Пирса. 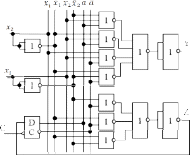 Рис.3.2.7. Вопросы для самопроверки по теме |
