МАТ.АН.+22+СО+СТО. Лекция Понятие числа. Комплексные числа
 Скачать 109.75 Kb. Скачать 109.75 Kb.
|
|
МАТ. АНАЛИЗ 22 СО СТО Лекция 1. 1. Понятие числа. Комплексные числа. Первой математической абстракцией было НАТУРАЛЬНОЕ ЧИСЛО. Первой арифметической операцией была операция СЛОЖЕНИЯ чисел. Множество 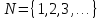 натуральных чисел ЗАМКНУТО относительно операции сложения, то есть, сложив два натуральных числа, мы получим снова натуральное число. натуральных чисел ЗАМКНУТО относительно операции сложения, то есть, сложив два натуральных числа, мы получим снова натуральное число.Операция ВЫЧИТАНИЯ, обратная операция к сложению, привела к расширению множества натуральных чисел, появились отрицательные числа и нуль. В результате сформировалось множество ЦЕЛЫХ чисел 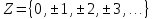 , которое замкнуто относительно операций сложения и вычитания. , которое замкнуто относительно операций сложения и вычитания. По мере дальнейшего развития общества появилась необходимость складывать одно и то же число много раз (например, в большом войске, поделенном на подразделения с определенным числом воинов в каждом). В результате таких повторений возникла операция УМНОЖЕНИЯ. Множество целых чисел 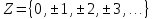 замкнуто относительно операций сложения, вычитания и умножения. Однако, обратная к умножению операция замкнуто относительно операций сложения, вычитания и умножения. Однако, обратная к умножению операция  ДЕЛЕНИЕ ДЕЛЕНИЕ уже «не укладывалась» в это множество и привела к дальнейшему расширению понятия числа. Появилось множество уже «не укладывалась» в это множество и привела к дальнейшему расширению понятия числа. Появилось множество 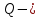 множество РАЦИОНАЛЬНЫХ (дробных) чисел. Рациональным числом называется дробь вида множество РАЦИОНАЛЬНЫХ (дробных) чисел. Рациональным числом называется дробь вида 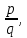 где где 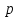 и и 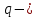 взаимно простые целые числа, за исключением взаимно простые целые числа, за исключением 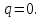 Условие взаимной простоты чисел Условие взаимной простоты чисел 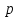 и и 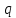 потребовалось, чтобы избежать многозначности определения рационального числа. Действительно, без этого условия рациональные числа потребовалось, чтобы избежать многозначности определения рационального числа. Действительно, без этого условия рациональные числа 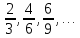 соответствуют одному рациональному числу соответствуют одному рациональному числу 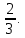 Однако, и операция умножения одного и того же числа на себя не избежала автоматизации в виде новой операции 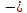 ВОЗВЕДЕНИЕ В СТЕПЕНЬ. Множество рациональных чисел ВОЗВЕДЕНИЕ В СТЕПЕНЬ. Множество рациональных чисел 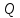 замкнуто относительно пяти арифметических операций: сложение, вычитание, умножение, деление (кроме деления на нуль!) и возведение в целую степень: замкнуто относительно пяти арифметических операций: сложение, вычитание, умножение, деление (кроме деления на нуль!) и возведение в целую степень: 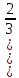 Но обратная к возведению в степень операция Но обратная к возведению в степень операция  ИЗВЛЕЧЕНИЕ КОРНЯ ИЗВЛЕЧЕНИЕ КОРНЯ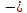 потребовала СУЩЕСТВЕННОГО (можно сказать ДВОЙНОГО) расширения понятия числа. потребовала СУЩЕСТВЕННОГО (можно сказать ДВОЙНОГО) расширения понятия числа. Во-первых, даже извлечение корня из натурального числа может вывести из множества рациональных чисел  Например, число Например, число 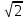 нельзя представить в виде несократимой дроби вида нельзя представить в виде несократимой дроби вида 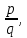 где где 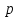 и и 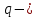 взаимно простые целые числа. Этот факт можно доказать, используя метод доказательства ОТ ПРОТИВНОГО. взаимно простые целые числа. Этот факт можно доказать, используя метод доказательства ОТ ПРОТИВНОГО.Предположим, что число 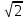 является рациональным числом, то есть является рациональным числом, то есть 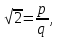 где где 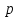 и и 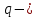 взаимно простые целые числа. Возведя это равенство в квадрат, мы получим равенство взаимно простые целые числа. Возведя это равенство в квадрат, мы получим равенство 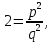 или, что то же самое, или, что то же самое, 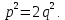 Из того, что число Из того, что число 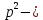 четное число, легко следует, что и число четное число, легко следует, что и число 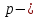 тоже четное число (если тоже четное число (если 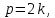 то то 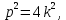 если если 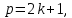 то то 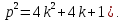 Итак, Итак, 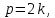 откуда следует, что откуда следует, что 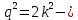 четное число, как и число четное число, как и число 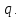 В результате, наше предположение о том, что В результате, наше предположение о том, что 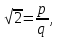 привело к тому, что числа привело к тому, что числа 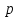 и и 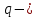 четные, что противоречит условию, что четные, что противоречит условию, что 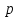 и и 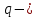 взаимно простые целые числа. взаимно простые целые числа. Итак, кроме рациональных чисел появились ИРРАЦИОНАЛЬНЫЕ числа. Совокупность рациональных чисел, дополненная иррациональными числами, образует множество 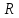 (real) ДЕЙСТВИТЕЛЬНЫХ чисел. Разница между рациональными и иррациональными числами хорошо видна при записи чисел в ДЕСЯТИЧНОЙ системе. (real) ДЕЙСТВИТЕЛЬНЫХ чисел. Разница между рациональными и иррациональными числами хорошо видна при записи чисел в ДЕСЯТИЧНОЙ системе.1). Если после десятичной запятой стоит конечное число цифр (в том числе нуль), то число  рациональное (в частности рациональное (в частности  целое). целое).Пример: 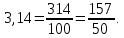 2). Если после десятичной запятой стоит бесконечное число цифр, при этом имеется периодически повторяющаяся группа чисел, то число  рациональное. рациональное.Пример: 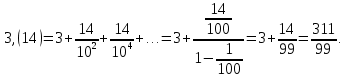 3). Если после десятичной запятой стоит бесконечное число цифр, не имеющих периодически повторяющейся группы чисел, то число  иррациональное. иррациональное.Пример: Число   Наглядное представление о множестве действительных чисел дает так называемая действительная ось Декарта. Она представляет собой бесконечную прямую, на которой отмечена точка  , соответствующая нулю, и задан масштаб с помощью точки , соответствующая нулю, и задан масштаб с помощью точки 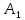 , соответствующей числу один. , соответствующей числу один. 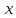 o  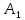 o 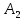 Рис. 1. Действительная ось Декарта. Каждой точке действительной оси соответствует действительное число и НАОБОРОТ. Например, точке 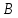 , показанной на рисунке 1, соответствует положительное число (точка расположена справа от точки , показанной на рисунке 1, соответствует положительное число (точка расположена справа от точки 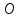 ), значение которого заключено в пределах от одного до двух. Чтобы уточнить это значение, откладываем вправо от точки ), значение которого заключено в пределах от одного до двух. Чтобы уточнить это значение, откладываем вправо от точки 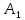 отрезок, равный по величине отрезку отрезок, равный по величине отрезку 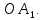 Получим точку Получим точку 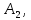 соответствующую числу два. Отрезок соответствующую числу два. Отрезок 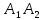 делим на десять равных частей, получаемые при этом точки соответствуют числам делим на десять равных частей, получаемые при этом точки соответствуют числам 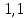 , 1,2,….., 1,9. По-видимому, точка , 1,2,….., 1,9. По-видимому, точка 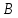 окажется между точками, соответствующими числам окажется между точками, соответствующими числам 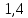 и и 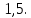 Отрезок между этими точками снова делим на 10 частей и если, например шестая из этих точек СОВПАДЕТ с точкой Отрезок между этими точками снова делим на 10 частей и если, например шестая из этих точек СОВПАДЕТ с точкой 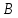 , то точке , то точке 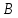 соответствует число соответствует число 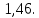 Однако, вероятность точного совпадения ОЧЕНЬ МАЛА, гораздо более вероятно, что процесс деления все меньшего и меньшего отрезка будет бесконечным. В этом случае, если не будет повторения цифр, точке 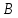 соответствует иррациональное число. соответствует иррациональное число.Во-вторых, извлечение корня четной степени из отрицательного числа не может быть реализовано в множестве действительных чисел. Так, например, число 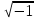 не может быть действительным числом, так как любое действительное число не может быть действительным числом, так как любое действительное число 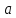 , при возведении в квадрат, дает в результате неотрицательное число , при возведении в квадрат, дает в результате неотрицательное число 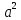 ! Таким образом, обратная операция ! Таким образом, обратная операция  извлечение корня извлечение корня  приводит к дальнейшему расширению понятия числа. Возникает множество приводит к дальнейшему расширению понятия числа. Возникает множество 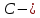 множество КОМПЛЕКСНЫХ чисел, в котором возможны все шесть арифметических операций, включая извлечение корня. множество КОМПЛЕКСНЫХ чисел, в котором возможны все шесть арифметических операций, включая извлечение корня.Определение 1. Комплексным числом называется число 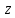 вида вида 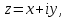 где где 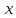 и и 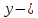 действительные числа, а действительные числа, а 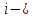 так называемая мнимая единица, удовлетворяющая условию так называемая мнимая единица, удовлетворяющая условию 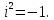 Первое слагаемое 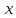 называется действительной частью комплексного числа называется действительной частью комплексного числа 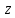 , а второе слагаемое , а второе слагаемое 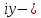 мнимой частью. мнимой частью. Примечание. Комплексное число 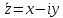 называется СОПРЯЖЕННЫМ к комплексному числу называется СОПРЯЖЕННЫМ к комплексному числу 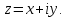 Так же, как действительным числам ставятся в соответствие точки действительной оси, комплексным числам можно поставить в соответствие точки КОМПЛЕКСНОЙ ПЛОСКОСТИ (см. рис. 2). При этом точку, соответствующую комплексному числу 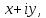 можно охарактеризовать и другими параметрами можно охарактеризовать и другими параметрами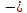 радиусом-вектором длины радиусом-вектором длины 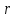 и его углом наклона и его углом наклона 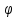 к оси к оси 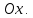  Рис.2. Изображение комплексного числа. Так как 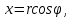 а а 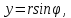 то комплексное число можно записать в так называемой ТРИГОНОМЕТРИЧЕСКОЙ ФОРМЕ: то комплексное число можно записать в так называемой ТРИГОНОМЕТРИЧЕСКОЙ ФОРМЕ: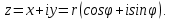 (1) (1)Число 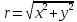 называется МОДУЛЕМ комплексного числа, а угол называется МОДУЛЕМ комплексного числа, а угол 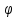 называется АРГУМЕНТОМ комплексного числа. Угол находится из соотношений называется АРГУМЕНТОМ комплексного числа. Угол находится из соотношений 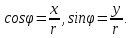 Рассмотрим все 6 операций над комплексными числами. При сложении складываются отдельно действительные части и мнимые части: 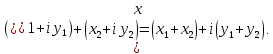 При вычитании вычитаются отдельно действительные части и мнимые части: 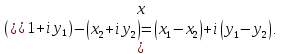 Умножение комплексных чисел производится по правилу умножения многочлена на многочлен, с учетом того, что 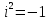 : :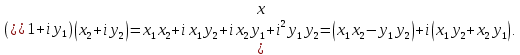 Примечание 1. Результатом умножения комплексного числа на сопряженное является действительное положительное число: 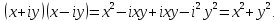 Примечание 2. При умножении комплексных чисел в тригонометрической форме их модули перемножаются, а аргументы складываются: 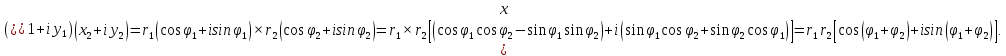 Деление комплексных чисел можно произвести путем умножения числителя и знаменателя на число, сопряженное со знаменателем: 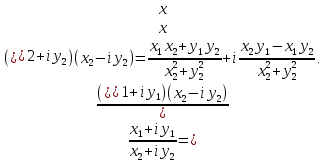 Примечание 2. При делении комплексных чисел в тригонометрической форме их модули делятся, а аргументы вычитаются: 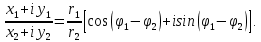 При возведении в степень 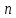 комплексного числа в тригонометрической форме его модуль возводится в степень комплексного числа в тригонометрической форме его модуль возводится в степень 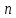 а аргумент делится на а аргумент делится на 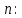 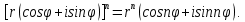 (2) (2) Доказательство формулы (2) проведем методом МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ, который состоит из двух шагов: - на первом шаге проверяют справедливость формулы для некоторого конкретного значения 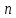 (как правило, при (как правило, при 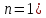 , , - на втором шаге доказывают, что если формула верна для при 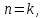 то она верна и для то она верна и для 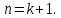 Итак, при 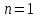 формула (2) верна. Более того, мы можем сказать, что она верна и для формула (2) верна. Более того, мы можем сказать, что она верна и для 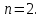 Это следует из формулы умножения (примечание 2). Это следует из формулы умножения (примечание 2).Предположим, что формула (2) верна для 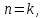 и докажем, что она справедлива и для и докажем, что она справедлива и для 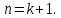 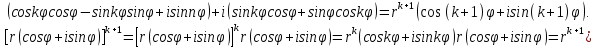 Извлечение корня из комплексного числа, заданного в тригонометрической форме, производится по ФОРМУЛЕ МУАВРА 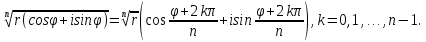 Доказывается путем возведения в степень 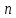 . .Примеры. 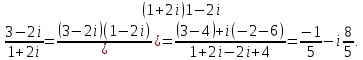 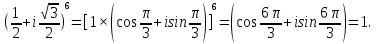 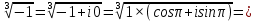 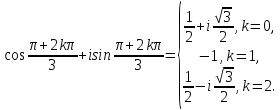 |
