МАТ.АН.+22+СО+СТО. Лекция Понятие числа. Комплексные числа
 Скачать 109.75 Kb. Скачать 109.75 Kb.
|
|
Следствие 1. Если 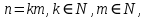 то справедлива формула то справедлива формула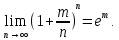 (2) (2)Действительно, поскольку 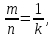 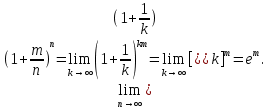 Следствие 2. Формулу (2) можно обобщить. Пусть 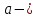 любое действительное число, тогда справедлива формула любое действительное число, тогда справедлива формула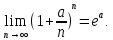 (3) (3)Поясним формулу (3) на двух примерах (заметим, что при 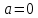 формула верна!) формула верна!)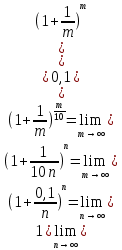 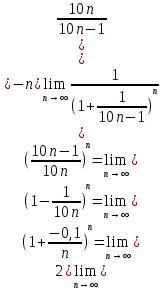 Применение формулы (3) при начислении сложных процентов. Предположим, что банк хочет начислять ЕЖЕДНЕВНО процент по внесенному депозиту в объеме 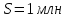 сроком на один год (так называемый СЛОЖНЫЙ процент). То есть, с учетом того, что уже через день исходная сумма увеличивается в соответствии с установленным банком, например, сроком на один год (так называемый СЛОЖНЫЙ процент). То есть, с учетом того, что уже через день исходная сумма увеличивается в соответствии с установленным банком, например, 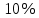 годовых. Как это сделать? Ответ кажется простым: надо разделить годовых. Как это сделать? Ответ кажется простым: надо разделить 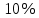 годовых на 365 дней и каждый день сумму умножать на коэффициент годовых на 365 дней и каждый день сумму умножать на коэффициент 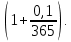 Теперь давайте подсчитаем, какая сумма получится к выдаче ровно через год, то есть через 365 дней: Теперь давайте подсчитаем, какая сумма получится к выдаче ровно через год, то есть через 365 дней: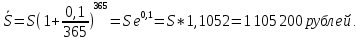 Таким образом, мы видим, что указанный выше простой подход к начислению ежедневных процентов приводит к тому, что через год потребуется выдать не планируемую сумму 1 100 000 рублей, а больше на 5 200 рублей. Как же ПРАВИЛЬНО делать ежедневные начисления процентов, чтобы к к концу года сумма выросла именно на 10 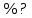 В таблице экспоненциальной функции В таблице экспоненциальной функции 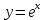 находим значение находим значение 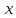 , при котором , при котором 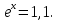 Это значение равно Это значение равно 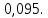 В результате мы нашли коэффициент В результате мы нашли коэффициент 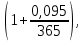 на который надо каждый день умножать сумму на который надо каждый день умножать сумму 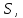 чтобы по истечении 365 дней сумма выросла ровно на чтобы по истечении 365 дней сумма выросла ровно на 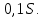 Примеры. 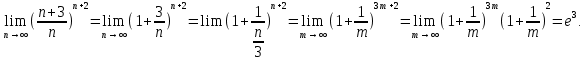 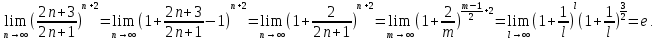 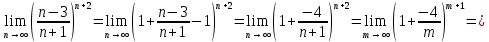 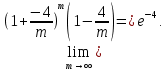 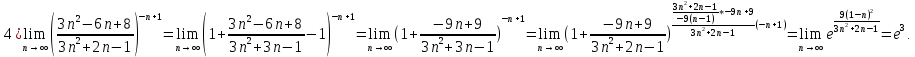 Задания для самостоятельной работы. Найти предел: 1) 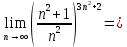 2) 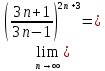 3) 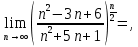 4) 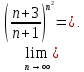 Лекция 4 Функция и ее предел. Определение 1. Величина 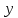 называется функцией независимой переменной называется функцией независимой переменной 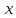 , если задан закон (правило), согласно которому каждому значению , если задан закон (правило), согласно которому каждому значению 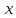 из области возможных значений (область определения функции) соответствует значение из области возможных значений (область определения функции) соответствует значение 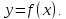 Функция может быть задана АНАЛИТИЧЕСКИ, например площадь круга 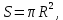 ТАБЛИЧНО (например, таблица синусов), или ГРАФИЧЕСКИ. ТАБЛИЧНО (например, таблица синусов), или ГРАФИЧЕСКИ.Определение 2. Множество 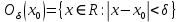 называется называется 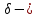 окрестностью точки окрестностью точки 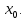 Имеется два эквивалентных определения КОНЕЧНОГО предела функции в заданной точке 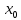 : определение по Коши, и определение по Гейне. : определение по Коши, и определение по Гейне.Определение 3 (по Коши). Число 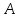 называется пределом функции называется пределом функции 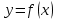 в точке в точке 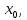 если для любого сколь угодно малого числа если для любого сколь угодно малого числа 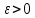 ( (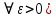 найдется такое число найдется такое число 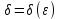 ( (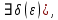 что как только выполняется условие что как только выполняется условие 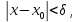 то имеет место неравенство то имеет место неравенство 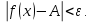 Если при этом Если при этом 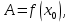 то функция то функция 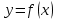 называется НЕПРЕРЫВНОЙ в точке называется НЕПРЕРЫВНОЙ в точке 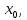 Определение 4 (по Гейне). Число 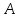 называется пределом функции называется пределом функции 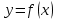 в точке в точке 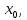 если для любой последовательности если для любой последовательности 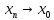 имеет место сходимость имеет место сходимость 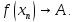 Если при этом Если при этом 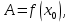 то функция называется НЕПРЕРЫВНОЙ в точке то функция называется НЕПРЕРЫВНОЙ в точке 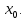 Из определения предела функции по Гейне автоматически вытекают следующие алгебраические свойства, аналогичные свойствам сходящихся последовательностей: 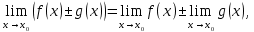 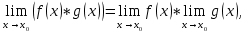 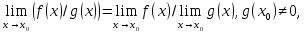 Если 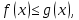 то то 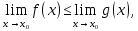 Следствие из свойства 4): если 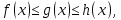 и 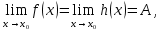 то то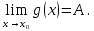 Определение 5 . Говорят, что число 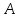 называется пределом функции называется пределом функции 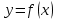 при при 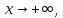 (при (при 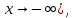 если для любой последовательности если для любой последовательности 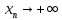 ( ( 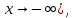 имеет место сходимость имеет место сходимость 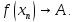 В этом случае прямая В этом случае прямая 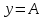 называется ГОРИЗОНТАЛЬНОЙ асимптотой к графику функции называется ГОРИЗОНТАЛЬНОЙ асимптотой к графику функции 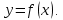 Заметим, что как в случае 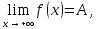 так и в случае так и в случае 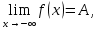 свойства пределов 1) свойства пределов 1)  4) остаются справедливыми. 4) остаются справедливыми.Определение 6 . Предел функции 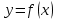 в точке в точке 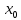 равен равен 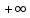 ( (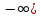 ( ( 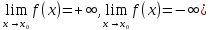 , если для любой последовательности , если для любой последовательности 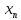 , такой что , такой что 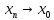 , имеет место сходимость последовательности , имеет место сходимость последовательности 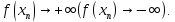 В этом случае вертикальная прямая 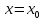 называется ВЕРТИКАЛЬНОЙ АСИМПТОТОЙ к графику функции называется ВЕРТИКАЛЬНОЙ АСИМПТОТОЙ к графику функции 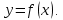 Первый замечательный предел 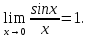  Рис. 1. Тригонометрический круг радиуса 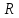 . .Докажем, что 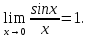 Для этого рассмотрим соотношение площадей треугольника Для этого рассмотрим соотношение площадей треугольника 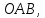 сектора сектора 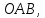 и треугольника и треугольника 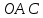 на рисунке 1: на рисунке 1: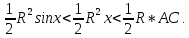 (1) (1)Так как 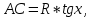 то неравенство (1) примет вид: то неравенство (1) примет вид: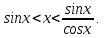 (2) (2)Заметив, что 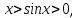 поделим неравенство (2) на поделим неравенство (2) на 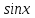 : :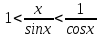 (3) (3)Из неравенства (3) следует неравенство для обратных величин: 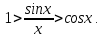 (4) (4)Переходя в неравенстве (4) к пределу при 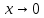 и учитывая следствие к свойству 4) и и учитывая следствие к свойству 4) и 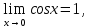 получим, что получим, что 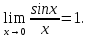 Заметим, что при доказательстве использована непрерывность функции Заметим, что при доказательстве использована непрерывность функции 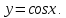 Непрерывные функции будут изучаться в следующей лекции. Непрерывные функции будут изучаться в следующей лекции.Второй замечательный предел 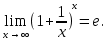 В предыдущей лекции мы показали, что последовательность 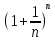 монотонно возрастает монотонно возрастает 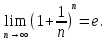 Если Если 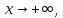 то для любого положительного то для любого положительного 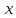 найдется такое натуральное число найдется такое натуральное число 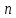 , что , что 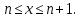 Из этого неравенства следует неравенство Из этого неравенства следует неравенство 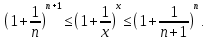 (5) (5)А поскольку 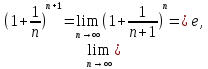 то в соответствии со следствием из свойства 4) получим 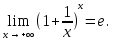 С помощью замены 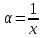 получаем другой вариант второго замечательного предела получаем другой вариант второго замечательного предела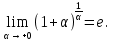 С помощью замены переменной 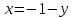 можно доказать, что можно доказать, что 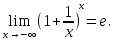 Примеры. Ниже приводятся примеры по раскрытию так называемых неопределенностей вида 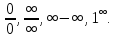 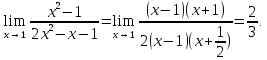 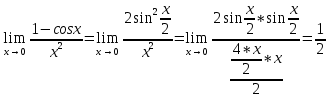 . .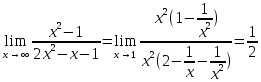 . .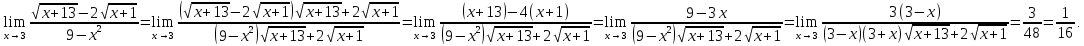 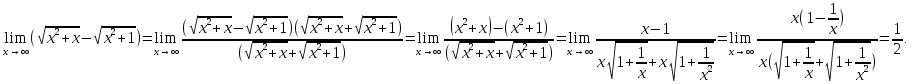 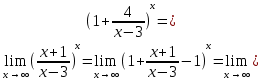 (обозначим 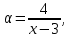 тогда тогда 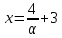 ) )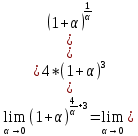 Задания для самостоятельной работы. Найти предел: 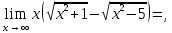 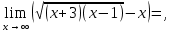 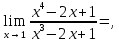 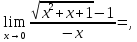 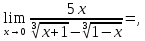 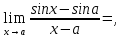 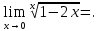 Лекция 5 Непрерывные функции. Точки разрыва. Определение 1. Функция 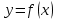 называется непрерывной в точке называется непрерывной в точке 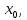 если если 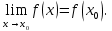 Определение 2. Число 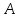 называется пределом функции называется пределом функции 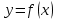 слева в точке слева в точке 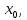 если если 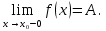 Этот предел также обозначают как Этот предел также обозначают как 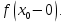 Символ Символ 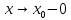 означает, что означает, что 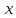 приближается к точке приближается к точке 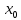 слева, то есть слева, то есть 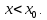 Если при этом Если при этом 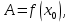 то функция называется НЕПРЕРЫВНОЙ СЛЕВА в точке то функция называется НЕПРЕРЫВНОЙ СЛЕВА в точке 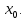 Определение 3. Число 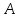 называется пределом функции называется пределом функции 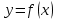 справа в точке справа в точке 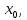 если если 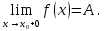 Этот предел также обозначают как Этот предел также обозначают как 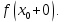 Символ Символ 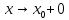 означает, что означает, что 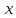 приближается к точке приближается к точке 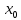 справа, то есть справа, то есть 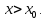 Если при этом Если при этом 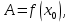 то функция называется НЕПРЕРЫВНОЙ СПРАВА в точке то функция называется НЕПРЕРЫВНОЙ СПРАВА в точке 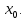 Определение 4. Если конечный предел слева 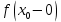 и конечный предел справа и конечный предел справа 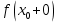 не равны, то говорят, что функция не равны, то говорят, что функция 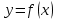 имеет в точке имеет в точке 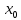 разрыв первого рода, если же хотя бы один из односторонних пределов равен бесконечности, то такой разрыв называется РАЗРЫВ ВТОРОГО РОДА. разрыв первого рода, если же хотя бы один из односторонних пределов равен бесконечности, то такой разрыв называется РАЗРЫВ ВТОРОГО РОДА.Очевидно, что если предел слева равен пределу справа в точке 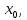 то есть, то есть, 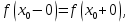 то функция то функция 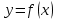 будет непрерывной в этой точке. будет непрерывной в этой точке. |
