МАТ.АН.+22+СО+СТО. Лекция Понятие числа. Комплексные числа
 Скачать 109.75 Kb. Скачать 109.75 Kb.
|
|
2.Понятие множества. Операции над множествами. МНОЖЕСТВО относится к тем математическим объектам, для которых нет СТРОГОГО определения. Под множеством будем понимать любое собрание некоторых объектов, мыслимое как единое целое, то есть имеющих нечто общее, что их объединяет. Выше мы познакомились с некоторыми ЧИСЛОВЫМИ множествами 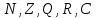 . Запись . Запись 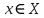 означает, что объект означает, что объект 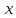 принадлежит множеству принадлежит множеству 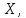 то есть, является его ЭЛЕМЕНТОМ. то есть, является его ЭЛЕМЕНТОМ. Множество 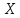 называется ПОДМНОЖЕСТВОМ множества называется ПОДМНОЖЕСТВОМ множества 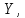 если любой элемент множества если любой элемент множества 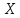 является элементом множества является элементом множества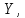 и обозначается и обозначается 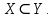 Например, Например, 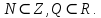 Множества делятся на конечные и бесконечные. Конечное множество можно задать простым перечислением, например, Множества делятся на конечные и бесконечные. Конечное множество можно задать простым перечислением, например, 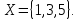 Бесконечные множества задаются с указанием определенного свойства, присущего элементам данного множества, например, Бесконечные множества задаются с указанием определенного свойства, присущего элементам данного множества, например, 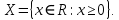 Среди множеств выделяют ПУСТОЕ множество 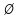 , в котором нет ни одного элемента, и так называемое УНИВЕРСАЛЬНОЕ множество , в котором нет ни одного элемента, и так называемое УНИВЕРСАЛЬНОЕ множество 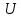 . Примером пустого множества служит множество . Примером пустого множества служит множество 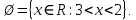 Под универсальным множеством Под универсальным множеством 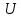 понимается наиболее широкое множество в данном конкретном рассуждении. То есть, когда все другие возможные множества являются лишь подмножествами понимается наиболее широкое множество в данном конкретном рассуждении. То есть, когда все другие возможные множества являются лишь подмножествами 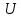 . Например, если мы говорим о студентах НГИЭУ (множество . Например, если мы говорим о студентах НГИЭУ (множество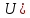 , то студенты инженерного института , то студенты инженерного института  это подмножество это подмножество 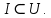 При этом, множество элементов множества При этом, множество элементов множества 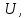 НЕ ПРИНАДЛЕЖАЩИХ НЕ ПРИНАДЛЕЖАЩИХ 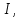 называется ДОПОЛНЕНИЕМ к множеству называется ДОПОЛНЕНИЕМ к множеству 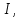 и обозначается и обозначается 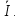 Объединением (суммой) 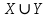 множеств множеств 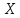 и и 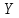 называется множество, каждый элемент которого принадлежит хотя бы одному из множеств называется множество, каждый элемент которого принадлежит хотя бы одному из множеств 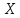 и и 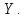 Пересечением (произведением) 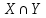 множеств множеств 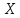 и и 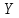 называется множество, каждый элемент которого принадлежит обоим множествам называется множество, каждый элемент которого принадлежит обоим множествам 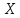 и и 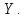 Геометрической иллюстрацией множеств и операций с ними являются так называемые КРУГИ ЭЙЛЕРА (см. рис. 3). На рисунке 3a) изображены множество 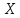 и дополнение к нему и дополнение к нему 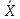 . Нетрудно видеть, что их объединением будет универсальное множество . Нетрудно видеть, что их объединением будет универсальное множество 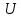 (прямоугольник). На рисунке 3b) изображено множество (прямоугольник). На рисунке 3b) изображено множество 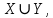 и на рисунке 3c) изображено множество и на рисунке 3c) изображено множество 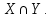 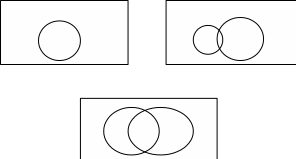 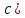 Рис. 3. Круги Эйлера. Задания для самостоятельной работы. Вычислить 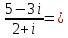 Вычислить 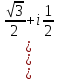 Вычислить 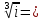 Лекция 2. Числовая последовательность и ее предел. Определение 1. Переменную действительную величину 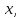 принимающую ПОСЛЕДОВАТЕЛЬНО (то есть, в порядке возрастания номера) значения принимающую ПОСЛЕДОВАТЕЛЬНО (то есть, в порядке возрастания номера) значения 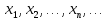 называют числовой последовательностью. Число называют числовой последовательностью. Число 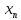 ( с номером ( с номером 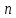 ) называют общим элементом последовательности. ) называют общим элементом последовательности.Примеры: 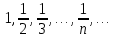 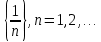 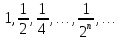 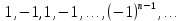 Определение 2. Постоянное число 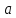 называется ПРЕДЕЛОМ числовой последовательности называется ПРЕДЕЛОМ числовой последовательности 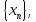 (обозначается (обозначается 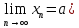 если для любого сколь угодно малого числа если для любого сколь угодно малого числа 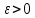 ( (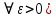 найдется номер найдется номер 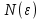 ( (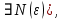 такой что при всех такой что при всех 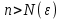 имеет место неравенство имеет место неравенство 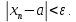 Проиллюстрируем это определение на примере. Докажем, что 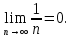 Для этого напишем несколько ЭКВИВАЛЕНТНЫХ неравенств: Для этого напишем несколько ЭКВИВАЛЕНТНЫХ неравенств: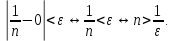 Если теперь взять натуральное число 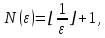 то из неравенства то из неравенства 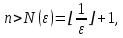 будет следовать неравенство будет следовать неравенство 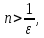 а значит, и неравенство а значит, и неравенство 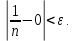 Определение 3. Переменная величина, имеющая пределом нуль, называется бесконечно малой величиной (б.м.в). Определение 4. Переменная величина 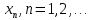 называется ОГРАНИЧЕННОЙ, если существует такое положительное число называется ОГРАНИЧЕННОЙ, если существует такое положительное число 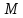 , что , что 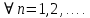 имеет место ограничение имеет место ограничение 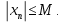 Переменная величина Переменная величина 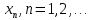 называется ограниченной СВЕРХУ, если существует такое положительное число называется ограниченной СВЕРХУ, если существует такое положительное число 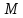 , что , что 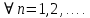 имеет место ограничение имеет место ограничение 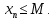 Свойства сходящихся последовательностей 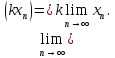 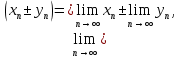 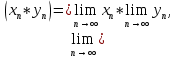 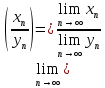 , при условии , при условии 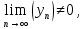 Если 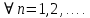 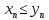 , то , то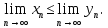 Следствие из свойства 4): Если 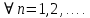 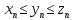 , и , и 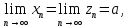 то и то и 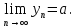 5)Сходящаяся последовательность ОГРАНИЧЕНА, то есть существует такое положительное число 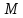 , что , что 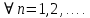 имеет место ограничение имеет место ограничение 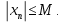 6)Если последовательность монотонно возрастающая, то есть 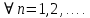 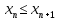 , и ограничена СВЕРХУ, то она имеет конечный предел. , и ограничена СВЕРХУ, то она имеет конечный предел.7)Если последовательность монотонно убывающая, то есть 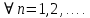 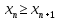 , и ограничена СНИЗУ, то она имеет конечный предел. , и ограничена СНИЗУ, то она имеет конечный предел.Доказательство свойств делается на основе определения предела. Докажем свойство 1): 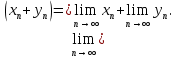 Дано: 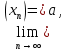 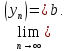 Это значит, что для любого сколь угодно малого числа Это значит, что для любого сколь угодно малого числа 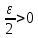 найдется номер найдется номер 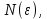 такой что при всех такой что при всех 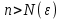 имеют место неравенства имеют место неравенства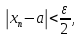 и и 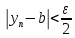 . . Раскрывая модули, получим неравенства 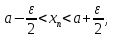 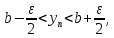 сложив которые, мы получим неравенство: 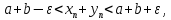 при всех при всех 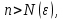 эквивалентное неравенству 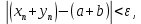 что и требовалось доказать. что и требовалось доказать.Примеры. 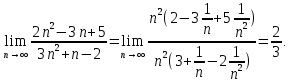 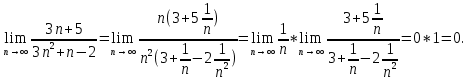 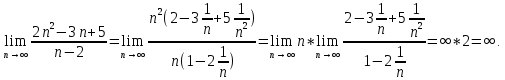 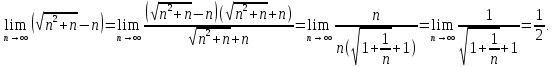 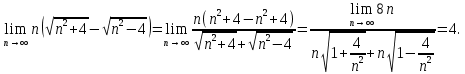 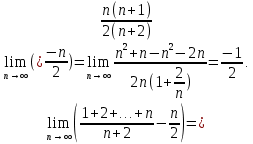 Докажем, что 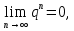 если если 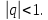 Заметим, имея в виду график функции 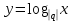 при при 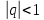 , что из неравенства , что из неравенства 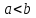 следует неравенство следует неравенство 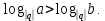 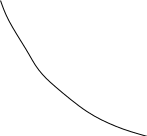 Рис.1. График функции 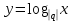 при при 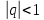 . .Напишем несколько ЭКВИВАЛЕНТНЫХ неравенств: 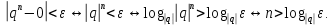 Если взять Если взять 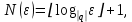 то при то при 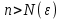 будет выполняться неравенство будет выполняться неравенство 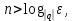 а значит, и неравенство а значит, и неравенство 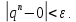 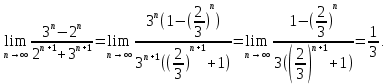 Докажем, что 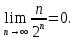 Действительно, так как 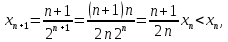 последовательность последовательность 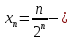 монотонно убывает! НО она ограничена снизу числом нуль. Значит, она имеет предел! монотонно убывает! НО она ограничена снизу числом нуль. Значит, она имеет предел!Обозначим этот предел 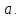 Переходя в равенстве Переходя в равенстве 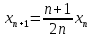 к пределу при к пределу при 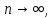 получим: получим: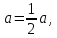 откуда и следует, что откуда и следует, что 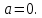 Определение 5. Говорят, что ПРЕДЕЛОМ числовой последовательности 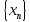 является является 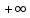 ( (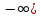 (обозначается (обозначается 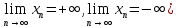 если для любого сколь угодно большого числа если для любого сколь угодно большого числа 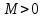 найдется номер найдется номер 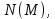 такой что при всех такой что при всех 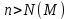 имеет место неравенство имеет место неравенство 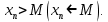 Определение 6. Переменная величина, имеющая пределом ∞, называется бесконечно большой величиной (б.б.в). Свойства бесконечно малых величин Если 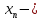 бесконечно малая величина и бесконечно малая величина и 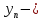 бесконечно малая величина, то и бесконечно малая величина, то и 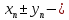 бесконечно малая величина. бесконечно малая величина.Если 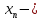 бесконечно малая величина, бесконечно малая величина, 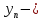 ограниченная величина, то произведение ограниченная величина, то произведение 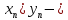 бесконечно малая величина. бесконечно малая величина.Задания для самостоятельной работы. Найти предел: 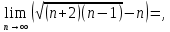 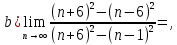 Доказать, что 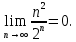 Лекция 3. Второй замечательный предел. Бином Ньютона. Докажем, что место формула 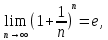 (1) (1)которая называется ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ. Для этого надо изучить свойства последовательности 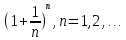 , каждый элемент которой представляет собой так называемый БИНОМ НЬЮТОНА: , каждый элемент которой представляет собой так называемый БИНОМ НЬЮТОНА: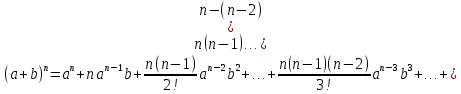 Заметим, что последние два слагаемых можно записать в более простом виде: 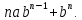 Эта формула доказывается методом математической индукции. Эта формула доказывается методом математической индукции.Вы эту формулу знаете для 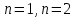 и и 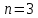 : :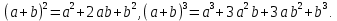 Если предположить, что формула верна для 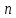 , то после выполнения произведения , то после выполнения произведения 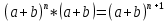 и приведения подобных членов получится эта же формула, в которой и приведения подобных членов получится эта же формула, в которой 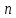 заменено на заменено на 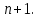 Действительно: Действительно: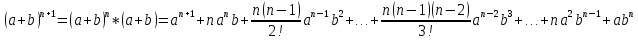 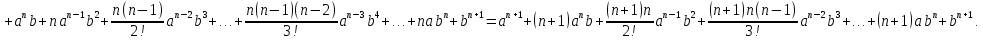 Для возведения двучлена 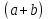 в большую степень полезно также использовать ТРЕУГОЛЬНИК ПАСКАЛЯ: в большую степень полезно также использовать ТРЕУГОЛЬНИК ПАСКАЛЯ: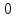 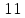 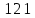 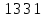 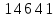 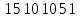 Например, 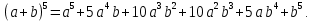 Рассмотрим поведение элементов последовательности 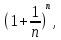 с возрастанием номера с возрастанием номера 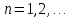 : : 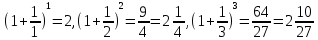 ,…. ,…. Мы видим, что 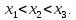 Для того, чтобы показать, что эта последовательность действительно монотонно возрастает, применим бином Ньютона 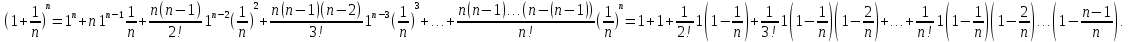 Нетрудно видеть, что следующий элемент 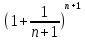 будет больше, чем будет больше, чем 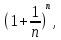 так как в его разложении каждое слагаемое, кроме первых двух, становится БОЛЬШЕ и добавляется еще одно, так как в его разложении каждое слагаемое, кроме первых двух, становится БОЛЬШЕ и добавляется еще одно, 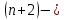 рое слагаемое рое слагаемое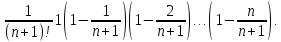 Заметим, что 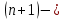 рое слагаемое в разложении рое слагаемое в разложении 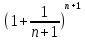 имеет вид имеет вид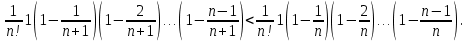 Итак, последовательность 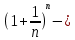 монотонно возрастает. Теперь докажем, что она ограничена сверху. монотонно возрастает. Теперь докажем, что она ограничена сверху. 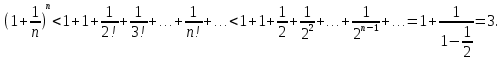 (Заметим, что при оценке сверху использовались неравенства 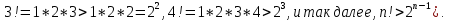 В соответствии со свойством 7) последовательность 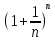 имеет предел, он равен числу имеет предел, он равен числу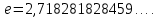 |
