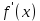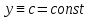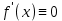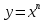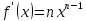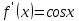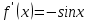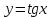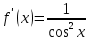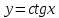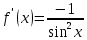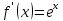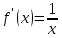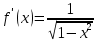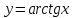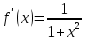МАТ.АН.+22+СО+СТО. Лекция Понятие числа. Комплексные числа
 Скачать 109.75 Kb. Скачать 109.75 Kb.
|
|
Определение 5. Если функция 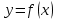 непрерывна в каждой точке интервала непрерывна в каждой точке интервала 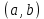 , то говорят, что она непрерывна на интервале , то говорят, что она непрерывна на интервале 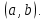 Свойства непрерывных функций. Из свойств 1) 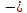 4) пределов функций вытекают соответствующие алгебраические свойства непрерывных функций: 4) пределов функций вытекают соответствующие алгебраические свойства непрерывных функций:Если 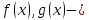 непрерывные функции в точке непрерывные функции в точке 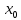 (на интервале (на интервале 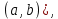 то тофункция 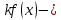 тоже непрерывна в точке тоже непрерывна в точке 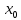 (на интервале (на интервале 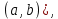 функция 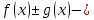 тоже непрерывна в точке тоже непрерывна в точке 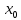 (на интервале (на интервале 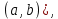 функция 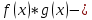 тоже непрерывна в точке тоже непрерывна в точке 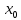 (на интервале (на интервале 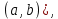 функция 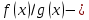 тоже непрерывна в точке тоже непрерывна в точке 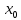 (на интервале (на интервале 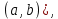 при условии при условии 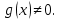 Непрерывность элементарных функций 1.Покажем, что ЛИНЕЙНАЯ функция 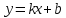 непрерывна на всей действительной оси, то есть на интервале непрерывна на всей действительной оси, то есть на интервале 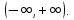 Действительно, пусть 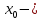 произвольная точка интервала произвольная точка интервала 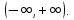 Применим определение предела по Коши. Для этого возьмем сколь угодно малое число Применим определение предела по Коши. Для этого возьмем сколь угодно малое число 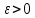 и запишем серию эквивалентных неравенств: и запишем серию эквивалентных неравенств: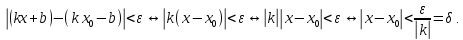 Итак, для любого, сколь угодно малого числа 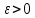 нашлось такое нашлось такое 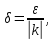 что как только что как только 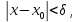 то выполняется неравенство то выполняется неравенство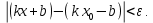 2.Покажем, что КВАДРАТИЧНАЯ функция 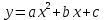 непрерывна на интервале непрерывна на интервале 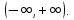 Действительно, поскольку функции 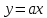 и и 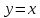 линейные, то по доказанному выше, они непрерывны на интервале линейные, то по доказанному выше, они непрерывны на интервале 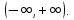 Но тогда их произведение Но тогда их произведение 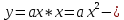 тоже непрерывная функция на интервале тоже непрерывная функция на интервале 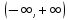 по свойству 3). Наконец, сумма непрерывных функций по свойству 3). Наконец, сумма непрерывных функций 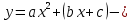 тоже непрерывная функция на интервале тоже непрерывная функция на интервале 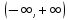 по свойству 2). по свойству 2).Следствие. Многочлен степени 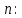 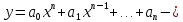 непрерывная функция на интервале непрерывная функция на интервале 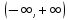 (доказывается методом математической индукции). (доказывается методом математической индукции).3.Покажем, что тригонометрическая функция 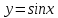 непрерывна на интервале непрерывна на интервале 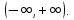 Действительно, пусть 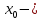 произвольная точка интервала произвольная точка интервала 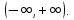 Применим определение предела по Коши. Для этого возьмем сколь угодно малое число Применим определение предела по Коши. Для этого возьмем сколь угодно малое число 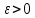 и запишем следующую цепочку неравенства: и запишем следующую цепочку неравенства: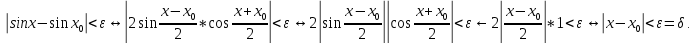 Заметим, что в этой цепочке неравенств использовано неравенство 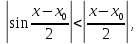 которое следует из неравенства (2) предыдущей лекции, а также очевидное неравенство которое следует из неравенства (2) предыдущей лекции, а также очевидное неравенство 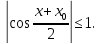 В результате этой цепочки неравенств мы можем сказать, что для любого сколь угодно малого числа В результате этой цепочки неравенств мы можем сказать, что для любого сколь угодно малого числа 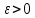 существует существует 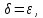 такое что при выполнении неравенства такое что при выполнении неравенства 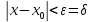 имеет место неравенство имеет место неравенство 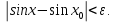 Итак, 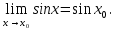 4.Аналогичным образом доказывается, что функция 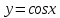 непрерывна на интервале непрерывна на интервале 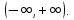 5. В соответствии со свойством 4) непрерывных функций непрерывными функциями являются функция 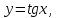 кроме точек, где кроме точек, где 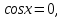 и функция и функция 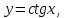 кроме точек, где кроме точек, где 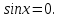 6.Функция 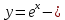 непрерывна на интервале непрерывна на интервале 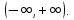 Действительно, пусть Действительно, пусть 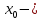 произвольная точка интервала произвольная точка интервала 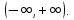 Применим определение предела по Коши. Для этого возьмем сколь угодно малое число Применим определение предела по Коши. Для этого возьмем сколь угодно малое число 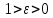 и запишем следующую цепочку неравенства: и запишем следующую цепочку неравенства: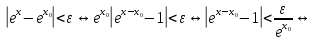 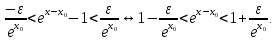 Если 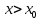 , то логарифмируя последнее неравенство, получим: , то логарифмируя последнее неравенство, получим: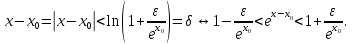 Итак, при выполнении неравенства 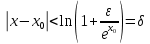 имеет место неравенство имеет место неравенство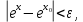 то есть то есть 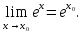 Аналогичным образом рассматривается случай, когда 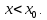 7.Функция 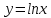 непрерывна на интервале непрерывна на интервале 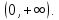 Действительно, пусть Действительно, пусть 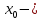 произвольная точка интервала произвольная точка интервала 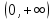 и и 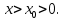 Возьмем сколь угодно малое число 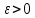 и запишем цепочку эквивалентных неравенств: и запишем цепочку эквивалентных неравенств: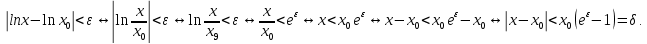 Итак, для любого 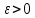 нашлось такое нашлось такое 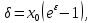 что при условии что при условии 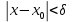 выполняется неравенство выполняется неравенство 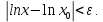 Это и означает в соответствии с определением предела по Коши, что 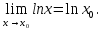 Аналогичным образом рассматривается случай, когда Аналогичным образом рассматривается случай, когда 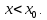 Задания для самостоятельной работы. 1.Будет ли функция 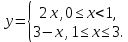 непрерывна на всем промежутке непрерывна на всем промежутке 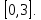 2.При каких 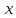 имеется разрыв непрерывности функции имеется разрыв непрерывности функции 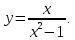 Нарисовать ее график. Нарисовать ее график.3.Является ли непрерывной функция 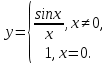 Нарисовать ее график. 4.Является ли непрерывной функция 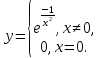 Нарисовать ее график. Лекция 6. Понятие производной Определение 1. Производной 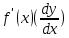 от функции от функции 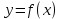 называется предел отношения приращения функции называется предел отношения приращения функции 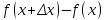 к приращению аргумента к приращению аргумента 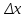 при стремлении последнего к нулю: при стремлении последнего к нулю: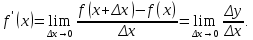 (1) (1)  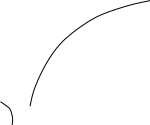 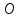 Рис. 1. Геометрический смысл производной и дифференциала. Геометрически производная означает тангенс угла 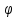 наклона к оси наклона к оси 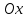 касательной к графику функции касательной к графику функции 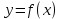 в точке в точке 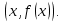 Определение 2. Дифференциалом 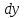 от функции от функции 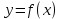 в точке в точке 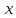 называется величина называется величина 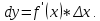 Геометрически дифференциал означает приращение функции, если бы она была ЛИНЕЙНОЙ. Геометрически дифференциал означает приращение функции, если бы она была ЛИНЕЙНОЙ. Механический смысл производной  это СКОРОСТЬ. Действительно, если это СКОРОСТЬ. Действительно, если 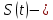 путь, пройденный за время путь, пройденный за время 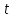 , а , а 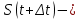 путь, пройденный за время путь, пройденный за время 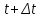 , то величина , то величина 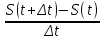 является СРЕДНЕЙ скоростью на участке пути является СРЕДНЕЙ скоростью на участке пути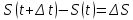 . Если же приращение времени . Если же приращение времени 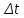 устремить к нулю, то получится мгновенная скорость движения устремить к нулю, то получится мгновенная скорость движения 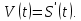 Свойства производных 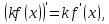 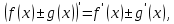 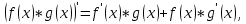 ( 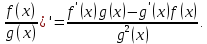 Если функция 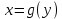 является ОБРАТНОЙ функцией для функции является ОБРАТНОЙ функцией для функции 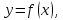 то то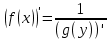 или или 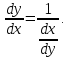 (2) (2)Свойства доказываются исходя из определения производной. В качестве примера докажем свойство 3. 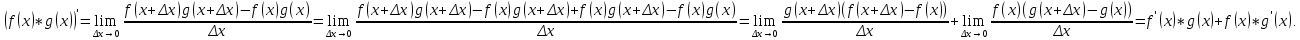 Таблица производных элементарных функций
Докажем справедливость некоторых формул из таблицы, используя определение производной. 1)Начнем с формулы 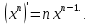 Для натуральных значений Для натуральных значений 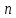 эта формула доказывается методом математической индукции. Для эта формула доказывается методом математической индукции. Для 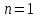 формула очевидна формула очевидна 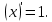 Докажем эту формулу для Докажем эту формулу для 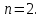 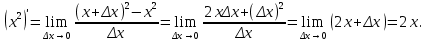 Предположим, что формула верна для 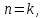 то есть то есть 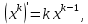 докажем, что тогда она верна и для докажем, что тогда она верна и для 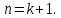 Действительно, Действительно, 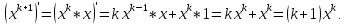 2)Докажем, что 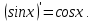 Действительно, Действительно, 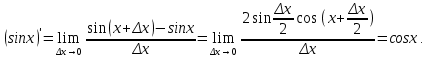 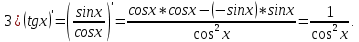 4)Поскольку функция 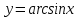 является обратной к функции является обратной к функции 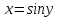 , то , то 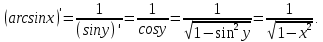 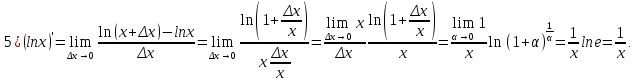 6)Поскольку функция 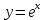 является обратной к функции является обратной к функции 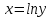 , то , то  Аналогичным образом доказываются и остальные формулы. Производная от сложной функции Очень часто встречаются так называемые СЛОЖНЫЕ (составные) функции вида 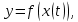 то есть то есть 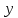 является функцией аргумента является функцией аргумента 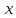 , а , а 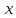 в свою очередь тоже является некоторой функцией аргумента в свою очередь тоже является некоторой функцией аргумента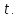 Например Например 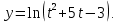 Требуется найти производную Требуется найти производную 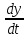 от функции от функции 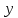 по аргументу по аргументу 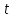 . Ниже представлена формула, как это сделать: . Ниже представлена формула, как это сделать: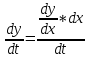 (3) (3)Действительно, по определению производной 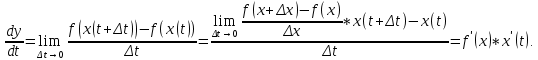 Поэтому, если 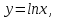 а а 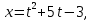 то то 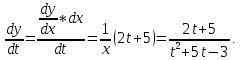 Сложная функция может быть не только двухступенчатой, но и трехступенчатой 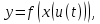 четырехступенчатой и так далее. Например, четырехступенчатой и так далее. Например, 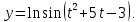 Соответственно, производная от сложной функции имеет три сомножителя, четыре сомножителя и так далее: Соответственно, производная от сложной функции имеет три сомножителя, четыре сомножителя и так далее: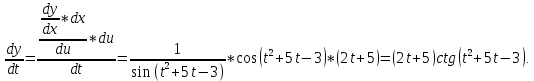 Логарифмическое дифференцирование Как видно из таблицы производных, дифференцирование степенной функции 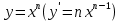 отличается от дифференцирования показательной функции отличается от дифференцирования показательной функции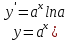 ). ). Обобщим эти формулы на случай сложной степенной и сложной показательной функций: 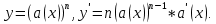 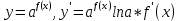 Однако, существует функция, которую можно назвать степенно- показательной: 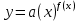 . Каким же образом взять производную от такой функции? Для решения этого вопроса прибегают к так называемому логарифмическому дифференцированию. . Каким же образом взять производную от такой функции? Для решения этого вопроса прибегают к так называемому логарифмическому дифференцированию.Если от исходной функции взять логарифм, то дифференцирование логарифма функции производится в полном соответствии со свойством (3): 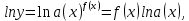 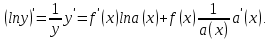 Умножив последнее равенство на 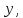 получим окончательную формулу: получим окончательную формулу: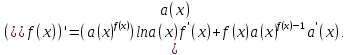 Задания для самостоятельной работы. Найти производную 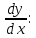 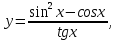 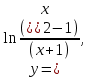 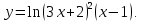 |