Матюшева ТРАНСП_Пояснительная записка-ЕСКД. Шнековый питательтранспортер
 Скачать 1.5 Mb. Скачать 1.5 Mb.
|
   Санкт-Петербургский государственный технологический институт Санкт-Петербургский государственный технологический институт(технический университет) Факультет: Инженерно-кибернетический. Кафедра Оптимизации химической и биотехнологической аппаратуры Учебная дисциплина «Машины для технологического транспортирования строительных материалов и изделий» Курс 4 Группа 372 КУРСОВОЙ ПРОЕКТ Тема: «Шнековый питатель-транспортер» Студент __________________ (Матюшева Е. ) Руководитель _________________ (Иваненко А.Ю.) Оценка за курсовой проект ______________ ________________ St.Petersburg г. Санкт-Петербургский государственный технологический институт (технический университет) Кафедра Оптимизации химической и биотехнологической аппаратуры Факультет: Инженерно-кибернетический. Кафедра Оптимизации химической и биотехнологической аппаратуры Учебная дисциплина «Машины для технологического транспортирования строительных материалов и изделий» Курс 4 Группа 372 Студент Матюшева Е. Дата __________________ Задание На курсовое проектирование Тема : «Шнековый питатель-транспортер» Цели и задачи проекта : Технологические и прочностные расчеты бункера и шнекового транспортера. Выбор стандартного шнекового транспортера. Содержание пояснительной записки:
Графический материал (чертежи):
Рекомендуемая литература:
Срок предоставления к защите: _________________________________________ Руководитель _________________ (Иваненко А.Ю.) Студент __________________ (Матюшева Е.) СОДЕРЖАНИЕ
Исходные данные для расчета
Плотность материала м = 2600 кг/м3; Пористость материала в состоянии насыпки 0 = 0,44. Компрессионная характеристика = 1,15/y0,09. Предел прочности при разрушении сжатием [] = сж = 50 МПа. Модуль упругости Е = 2,21010 Па. Угол естественного откоса е = 33 град. Угол внешнего трения покоя порошкообразного мела о стальную пластину п = 24 град. Эффективный угол внутреннего трения э = 50 град. Угол внутреннего трения = 42 град. Мгновенная функция истечения р = 27 y0,46 ;
Насыпная плотность мела ρ = ρм (1-ε0) = 2600 (1- 0,44) = 1456 кг/м3. Объемная производительность установки Q = G/ρ = 40000/1456 =27,47 м3/ч = 7,63∙10-3 м3/c. Объем бункера найдем из расчета 8-часовой производительности установки Vб = Q∙τ = 27,47·8 = 220 м3. Выполним бункер цилиндро-коническим. Примем диаметр цилиндрической части D = 5 м; высоту цилиндрической части Hц = 10 м. Тогда объем цилиндрической части бункера составит Vц = Hц ·πD2/4 = 10·3,14·52/4 = 196 м3. Рассчитаем объем конического днища бункера, выполненного в виде усеченного конуса. 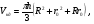 где h - высота усеченного конуса; R – радиус большого основания конуса; R = D/2 = 2,5 м; r0 - радиус малого основания конуса; r0 = d/2. Минимальный размер отверстия истечения примем из условия обеспечения заданной производительности загрузки V = 7,63∙10-3 м3/c. 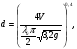 где λи – коэффициент истечения; λи = 0,2 ÷ 0,5. Размер d найдем с запасом, приняв λи min = 0,2. 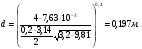 Окончательно примем диаметр отверстия истечения d = 200 мм. r0 = d/2 = 100 мм = 0,1 м. Из [ 4 ] при п = 24 град и = 42 град находим, что максимальный угол наклона образующей конической части бункера θ, при котором обеспечивается свободное истечение материала, составляет 20 град. Тогда угол α = 70 град. Высота днища h = (R-r0)·tg α = (2,5-0,1) tg 700 = 6,594 м ≈ 6,6 м. Объем усеченного конуса по формуле (5) 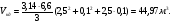 Общий объем бункера V = Vц + Vкд = 196 + 44,97 = 240,97 м3, что удовлетворяет условию обеспечения работы бункера в течение 8,77 часа. Окончательно принимаем следующие геометрические размеры бункера:
3 Прочностной расчет бункера Определим распределение напряжений σ1 по глубине бункера, предварительно вычислив максимальную величину насыпной плотности ρн. В рассматриваемом случае материал уплотняется под действием максимального главного напряжения, т.е σy = σ1. Максимальное главное напряжение в таком бункере 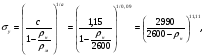 где ρн – максимальная величина насыпной плотности материала в бункере, кг/м3. Гидравлический радиус бункера R = D/4 = 5/4 = 1,25 м; коэффициент внешнего трения покоя fп = tg φп = tg 240 = 0,445; коэффициент бокового давления ζ = (1 – sin )/(1 + sin )=(1 – sin 420)/(1 + sin 420) = 0,198. При этих данных и при максимальной координате Z = Hц + (D/2)tg700 = 10+6,87=16,87 м напряжение 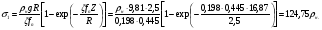 Так как σ1 = σy, то 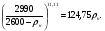 Решая полученное уравнение методом последовательных приближений, получим ρн = 1604 кг/м3. Для цилиндрической части бункера вычислим σ1 для трех значений Z (4; 7 и 10 м): 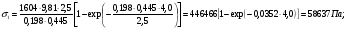 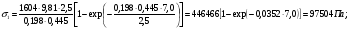 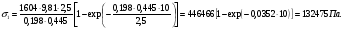 Для расчета напряжений в конической части бункера предварительно определим величину B: B = (cos2 + ζ sin2) (fп + ctg ) tg = = (cos2700 + 0,198 sin2700) (0,445 + ctg 700) tg 700 = 0,649. Для конической части силоса рассчитаем σ1 для трех значений Z = 2,0; 4,0 и 6,0 м. 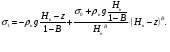 При Z = 2,0 м 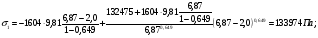 при Z = 4,0 м 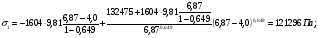 при Z = 6,0 м 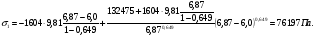 По расчетным значениям построим график функции σ1 = f (Z) (см. рис. 1). Усилия на стенках бункера определим на следующих глубинах: от поверхности материала – на глубине Z, равной 0; 2,5; 5; 7,5 и 10 м; от основания конуса – на глубине Z, равной 0; 3 и 6 м. Для цилиндрической части бункера, расположенной выше опорных лап, усилия на единицу длины окружности P0 и единицу длины образующей Pп (без учета веса корпуса бункера) будут определяться следующими выражениями: 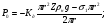 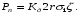 Величины σ1 для соответствующей глубины будем находить из графика (см. рис. 1 ). Принимая коэффициент Кд, учитывающий возможность обрушения материала в результате его слеживания, равным 2, получим: При Z = 0 P0 = -98245 Н/м и Pп =0; При Z = 2,5 м 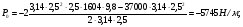 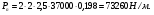 При Z = 5,0 м 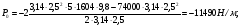 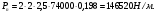 Для цилиндрической части бункера, расположенной ниже опорных лап, усилия P0 и Pп будут определяться следующими выражениями: 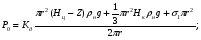 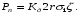 При Z = 5,0 м 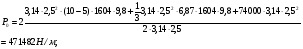 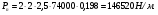 При Z = 7,5 м 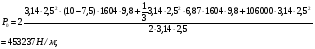 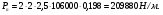 При Z = 10 м 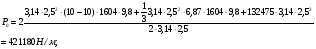 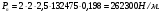 Для определения усилий P0 и Pп в конической части бункера воспользуемся уравнениями: 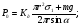 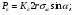 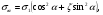 где r –радиус конуса на расстоянии z, м; m – масса материала ниже сечения z, кг. 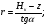 а масса материала приближенно 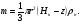 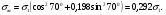 При Z = 0 r = 2,5 м 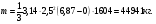 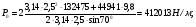 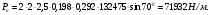 При Z = 2 м 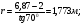 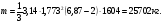 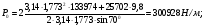 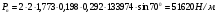 При Z = 4 м 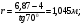 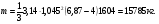 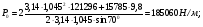 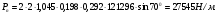 При Z = 6 м 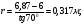 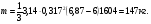 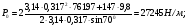 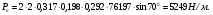 При Z = 6,87 м P0 ≈ 0 и Pп ≈ 0. Результаты расчетов сведем в табл. 1. Таблица 1 Расчетные значения нормальных напряжений σ1, усилий на единицу длины окружности P0 и единицу длины образующей Pп
По расчетным величинам строим графики функций P0 (Z) и Pп (Z) (см. рис. 1). Полученные значения усилий позволяют рассчитать толщину стенок бункера. Максимальные усилия в стенке бункера возникают на глубине Z = 10 м. Толщина стенки бункера, рассчитанная по максимальным усилиям δ ≥ (P02 + Pп2)0,5/[σдоп] = (4211802 + 2623002)0,5/(215·106) = 0,0024 м. С учетом конструктивных добавок и добавок на коррозию примем толщину стенки бункера δ = 5 мм. 4 Расчет и выбор шнекового питателя-транспортера Горизонтальный шнековый транспортер (или винтовой конвейер) [1] обычно (рис.2) состоит из желоба 5, в котором вращается винт 3. Вал винта поддерживается двумя концевыми подшипниками и промежуточными подвесными подшипниками 2. Привод конвейера включает электродвигатель 8, редуктор 7 и две муфты 6. При вращении винта в направлении стрелки на транспортируемый груз действуют поперечные составляющие сил давления винтовых лопастей на перемещаемый груз и сил трения этого груза о лопасти, в результате чего центр массы груза С смещается влево. Возникающий при этом момент силы тяжести груза относительно центра винта О препятствует дальнейшему вращательному движению груза, и последний перемещается вдоль оси конвейера в направлении транспортирования, как гайка вдоль винта, а затем высыпается из разгрузочного отверстия 4 (см. рис.2). В нашем случае транспортер устанавливается под бункер так, как показано на рис.3. Длина транспортирования L = 5,0 м. Производительность транспортера G = 40 т/час = 11,11 кг/с. Рис.2. Схема горизонтального шнекового транспортера Рис.3. Схема шнекового питателя Диаметр винта транспортера можно найти [1] из уравнения  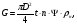 где t – шаг винта; для горизонтального конвейера t = k D; n – частота вращения, об/с; ψ – коэффициент наполнения желоба; для мела, который является легким малоабразивным грузом ψ = 0,32 [2]; ρн – насыпная плотность мела; выше (в п.2) было рассчитано ρн = 1456 кг/м3. Частота вращения вала винта определяется из соотношения [3] 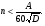 При рекомендуемых в [1,2] для легких малоабразивных материалов коэффициентах ψ = 0,32; А=50; k=1,0 получим 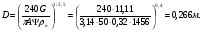 Диаметр винта транспортера выбирают из стандартного ряда ГОСТ 2037-82 [1]. Из указанного ряда выбираем D = 320 мм. Диаметр вала винта (мм) [1]  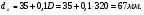 Принимаем диаметр вала винта равным 70 мм. Частота вращения вала винта 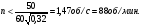 Это значение числа оборотов попадает в интервал, рекомендованный для частот вращения горизонтальных шнековых конвейеров, транспортирующих насыпные измельченные минералы (см. табл. 3.1 в книге Зенкова [1]). Уточним производительность транспортера по уравнению (1) 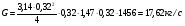 , , что несколько больше требуемой производительности (11,11 кг/с). Для снижения производительности транспортера до требуемой величины снизим число оборотов шнека до 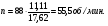 Примем число оборотов шнека n = 60 об/мин. Мощность привода транспортера 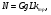 где L – длина транспортирования; L = 5,0 м; kтр – коэффициент сопротивления груза перемещению; для мела kтр = 1,6. 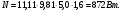 Мощность электродвигателя с учетом КПД = 0,8 Nдв = N / = 872 / 0,80 = 1100 Вт. Принимаем электродвигатель мощностью 1,2 кВт. Максимальный крутящий момент на валу винта 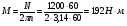 Наибольшая действующая на винт продольная сила 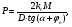 где kc – коэффициент, учитывающий, что радиус винта больше, чем радиус, на котором расположена равнодействующая сил сопротивления винта вращению; kc = 1,25 ÷ 1,43; примем kc = 1,35; α – средний угол подъема винтовой линии; 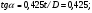 α = arctg 0,425 = 23 град; φп – угол внешнего трения измельченного материала о сталь; φп = 24 град. 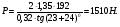 5 Список использованных источников
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 5
5