экзаменационный билет 7. Билет7 павлов Кирилл 3Г. сибирская государственный университет геосистем и технологий
 Скачать 116.97 Kb. Скачать 116.97 Kb.
|
|
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение Высшего образования «СИБИРСКАЯ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ» (ФГБОУ ВО «СГУГиТ») Кафедра физической геодезии и дистанционного зондирования Экзаменационный билет №7 Выполнил студент группы Павлов К.А. 3Г Проверил: Канушин В.Ф. Новосибирск 2023 Экзаменационный билет №7 1. Метод Лапласа определения нормального потенциала силы тяжести. 2.Применение интегральных уравнений для решения краевых задач. 3. Вычисление потенциала шара радиуса 500км с плотностью 13.0341г/ 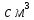 при G=6.672 при G=6.672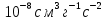 Ответы на билет №7 3) Задача:  1) Теорема Лапласа: Смысл введения нормального потенциала заключается в переходе от изучения потенциала W силы тяжести реальной Земли к изучению малой величины Т = W – U. Введение нормального потенциала преследует две цели: в одном случае нормальное поле рассматривают как модель, приближенно представляющую реальное поле Земли; во втором нормальное поле используют как отсчетное, относительно которого находят аномальный потенциал. Т. е. в первом случае речь идет об использовании нормального поля вместо реального, а во втором - об определении отличия реального поля от нормального. В обоих случаях стараются выбирать нормальное поле так, чтобы аномальный потенциал был мал. Тогда в первом случае величиной Т просто пренебрегают, а во втором появляется возможность строить теорию ее определения в линейном приближении, не учитывая члены порядка квадрата аномального потенциала. В качестве нормального всегда стараются выбрать потенциал, который можно описать по возможности простыми аналитическими выражениями, с тем, чтобы в нормальном поле легко решались задачи геодезии, геофизики, небесной механики. Таким образом, нормальный потенциал можно определить, как потенциал достаточно простого вида, по возможности близкий к действительному 2) При аналитическом исследовании краевых задач для обыкновенных дифференциальных уравнений во многих случаях удобнее рассматривать эквивалентные им интегральные уравнения, содержащие полную математическую постановку описываемой задачи и находящие эффективное применение при определении собственных значений и функций. Развитие численных методов позволяет использовать интегральные уравнения и для непосредственного численного решения краевых задач, не прибегая к дифференциальным уравнениям. Эквивалентное преобразование обыкновенных дифференциальных уравнений с краевыми условиями к интегральным уравнениям осуществляется обычно посредством функции Грина . Стоит отметить, что обратные переход не всегда возможен: известны многие случаи описания краевых задач в виде интегральных уравнений, не имеющих аналогов среди дифференциальных уравнений и поэтому не допускающих соответствующих преобразований без применения каких-либо приемов аппроксимации. |
