Сыйымдылыы
 Скачать 228.11 Kb. Скачать 228.11 Kb.
|
|
Қатты қосылыстардың мольдік жылу сыйымдылықтары 1.2 кесте
Сондай-ақ үш атомды қосылыстардың молекулалық жылу сыйымдылығы шамамен 18 кал/ градмоль , ал төрт атомды қосылыстардікі – 24 кал/ градмоль болуға тиіс т.с.с. Сондай-ақ үш атомды қосылыстардың молекулалық жылусыйымдылығы шамамен 18 кал/ градмоль , ал төрт атомды қосылыстардікі – 24 кал/ градмоль болуға тиіс т.с.с. Бұл қорытынды Джоуль мен Копптыңтәжірибе жүзінде тағайындаған заңынадәл келеді; бұл заң бойынша қаттықосылыстардыңмолекулалықжылу сыйымдылығы осы қосылыстардың құрамына кіретін элементтердіңатомдықжылу сыйымдылықтарыныңқосындысынатеңболады. Джоуль мен Копп заңы бөлшектердің тербелістері біріне-бірі тәуелсіз деп есептелетін жоғары температураларда ғана дұрыс болады. 2-ші кесте Джоуль мен Копп заңы бөлме температурасында бірқатар қосылыстар үшін айтарлықтай дәл келетіндігі көрінеді. Температура төмендегенде қатты заттардың барлығының да жылу сыйымдылығы төмендейді. Қатты денелердің жылу сыйымдылығының температураға байланысты төмендеуі график түрінде 1.1-ші суретте көрсетілген. Температура абсолютнольгеқарайжуықтағандақаттыденелердіңбарлығыныңдажылусыйымдылығынольгежуықтайды.Қатты денелердің жылу сыйымдылықтарының өте төмен температуралардағы өзгерісін кванттық механиканың негізінде ғана түсіндіруге болады. 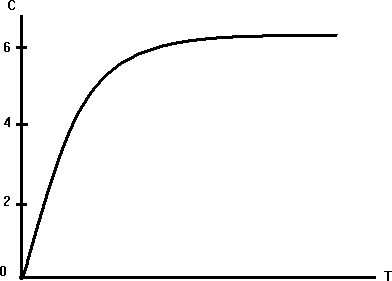 1.1-сурет Біз кванттық механика бойынша жеке бөлшектердің энергиясы тек үздік-үздік өзгеретіндігін білеміз. Кристалдық решеткадағы атомдардың (иондардың) тербеліс энергиясы да осылайша өзгереді. Сонда решеткадағы тербеліп тұратын бөлшектің энергиясының мөлшері h шамаға өзгереді, мұндағы h- Планк тұрақтысы, ол 6,6 10- 27 эргсекке тең, ал 2 - бөлшектің тербеліс жиілігі. Бір еркіндік дәрежесіне келетін 1 kT орташа энергия h шамаға қарағанда әлдеқайда үлкен болатын температураларда бөлшектің тербеліс энергиясы Ттемператураға байланысты үздіксіз өзгереді деп есептеуге, демек, оған классикалық теорияны қолдануға 2 болады. 1 kT орташа энергия энергияның h квантымен шамалас болатын төмен температуралардағы есеп кванттық механиканың негізінде жүргізілу керек. Кристалдық решеткадағы бөлшектің тербеліс жиілігі шамасында болады, сонда 1012 сек- 1 2 1 kT> h теңсіздіктен есептеудің классикалық тәсілі мына шартты қанағаттандыратын температуралар үшін дұрыс болатындығы шығады: 2 6,6 10- 27 1012 Т > 1,4 10- 16 °К 100°К. Сонымен, бөлме температураларында (Т 300°К) жылу сыйымдылықты есептеуге классикалық тәсілдің жарайтындығы көрінеді, ал – 200°С шамасындағы температураларда жылусыйымдылықты есептеу үшін кванттық теорияны қолдану керек. Қатты денелер жылу сыйымдылығының кванттық теориясы негіздерін Эйнштейн салған болатын. Сонан кейін Дебай решетканы жасап тұрған бөлшектердің төмен температуралардағы өз ара әсерлерінің ролін еске алған. Дебай жеке бөлшектердің тербелістерін емес тұтас решеткадағыорныққантербелістердіқарастырған.Олкристалдықрешеткадағыакустикалықтолқындардыдақамтитынжиіліктеріәртүрлітұрғынтолқындардыңорнығатындығынкөрсетті. Кристалдық решетканың осы барлық тербелістерінің энергияларын жинақтап және кванттық механика бойынша олардың температураға тәуелділігін есепке алып, Дебай тәжірибелермен өте жақсы үйлесетін нәтижелерге жеткен. Өте төмен температураларда қатты денелердің жылусыйымдылығыабсолют температураның үшінші дәрежесіне пропорционалболыпөзгереді. Дебай теориясының артықшылдығы – бұл теория кристалдардағы жылулық тербелістерді олардың акустикалық тербелістерімен байланыстырады. Совет физигі Л.И. Мандельштам кристалдарда серпімді жылулық толқындардың болуы кристалдан шашырап шығатын жарықтың сипатына әсер ететін болу керек деп көрсетті ( ІІІ томда айтылады). Л.И. Мандельштамның алдын ала болжап айтқанын совет физигі Е.Ф. Гросс іс жүзінде анықтаған, сонымен, қатты денелерде серпімді жылулық тербелістердің бар екендігі эксперимент жолымен дәлелденген болып табылады. 1.1. Кристалдың жылу сыйымдылығы (классикалық теория) 19 ғасырда Дюлонг және Пти қатты денелердің жылу сыйымдылығын зерттей отырып, бөлме температурасына жақын температураларда 1 атомдық кристалдың жылу сыйымдылығын анықтады. Cv= 25 Дж/ (моль∙К) 3 Бұл температура өскен сайын жылу сыйымдылығы өсетінің аңғартты. Кешіректе эксперимент нәтижесі көрсеткендей температура күрт төмендегенде жылу сыйымдылығы да төмендейді екен. Абсолют температурада диэлектрлік кристалдарда Т3 болып, ал металдарда - 𝛼Т Т пропорция заңы бойынша өзгереді. (мұндағы 𝛼 , заттардың қасиетіне байланысты тұрақты шамалар) . 1.2-ші суретте күміс жылу сыйымдылығының температураға тәжірибе жүзіндегі байланыстылығы көрсетілген. Қатты денелердің жылу сыйымдылығының температуралық қасиеті эксперимент зерттеулер бойынша Дюлонг және Пти заңдарында классикалық бірнеше моделін қарастырамыз. Бір атомдық кристалдық қатты дененің ішкі құрылысының классикалық моделінің жинағын квазитығыз (квазиупругих) күштердің әсерінің кристалдық торлардың түйіндерінде тербеледі деп қарастырамыз. Әр бір атомның тербелісін үштік бос дәрежемен бейнелеуге болады, онда бұл жағдайда қатты денені классикалық осциллятордың жиынтығы ретінде қабылдауға болады. Олардың саны бір мольде Авогадро тұрақтысының үшеуіне көбейтілген. Бұндай мәліметті біле отыра ішкі энергияны табу қиынға соқпайды: Е=3NkT A Ал молярлық жылу сыйымдылық dE Cv=DT =3 NAk=3R (1.1) Классикалық көзқараста металдың жылу сыйымдылығы әлдеқандай үлкен болу керек. Металдарда электрон өткізгіштер бар, бірақ классикалық тұрғыдан ол үш дәрежелі болып келеді. Егер оның саны атом санына тең деп алсақ (бос бөлшектер сияқты) CЭ= 1,5 R т.б. оны 50%-ға ұлғайтады. Шынында да бұл жоқ, Дюлонг және Пти мұны металдарда да ескерілген. Бұл модельдің келісілген температураның жылу сыйымдылыққа байланысы анықталмай отыр, диэлектрик пен металдардың айырмашылығын өте кіші температурада және де Дюлонг пен Пти заңындағы ерекше алмаз, бериллий, бор, кремний, алюминий бөлме температурасында жылу сыйымдылығы 3R –ге жақын өсті. Жылу сыйымдылықтың қатаң теориясын тек кванттық механикалық базада ғана құруға болады. 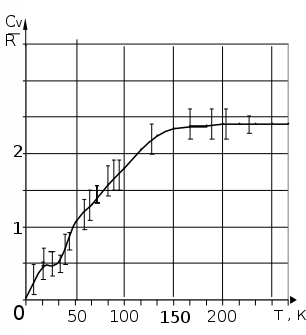 140 120 100 80 60 40 20 0 1.2-сурет Өткен ХХ ғасырдың басында В. Нернст бір топ ғалымдармен бірге көптеген қатты денелердің жылу сыйымдылықтарын үлкен температура аралықтарында (соның ішінде абсолют нөл температураға жақын маңайларда) зерттеп өлшеу жұмыстарын кеңінен жүргізді (Нернст Вольтер Фридрих Герман 1864-1941ж неміс физигі және химигі). Бұл жұмыстардың нәтижесінде барлық қатты денелердің жылу сыйымдылықтары ( Cржәне Cv) температура функция екені және абсолют нөл температураға жақын аймақтарда нөлге айналатыны анықталады: Cр(Т⟶ 0) = Cv(Т⟶ 0) =0 (1.2) Сондай-ақ, тәжірибе нәтижелеріне сәйкес қатты күйдегі химиялық элементтердің мольдік жылу сыйымдылықтары температура жоғарылаған сайын арта түсіп, Дюлонг-Пти заңымен анықталатын өзінің шектік мәніне ұмтылады екен. Мысал ретінде 1.3-суретте қорғасын, мыс және алмас үшін жылусыйымдылығы мен температура арасындағы байланысты сипаттайтын тәжірибе жүзінде алынған қисықтар келтірілген. Егер қорғасынның жылу сыйымдылығы 6 кал/моль∙К (25 Дж/моль∙К) мәніне 100 Көзінде-ақ жетіп үлгерсе, ал мыста бұл тек 400 К , алмаста - 1270 К (1000°С) ғана байқалады. Тәжірибе көптеген элементтер үшін Дюлонг және Пти заңы кристалдардың балқу температурасының аймағында орындалатынын және жылу сыйымдылығының мәнінің тұрақтылығы көптеген заттар үшін бөлме температураларына дейінгі аралықтарда сақталатынын көрсетіп отыр. Cv- нің термодинамикалық өрнегіне байланысты Cv= ∂U ∣ ∣ , (1.3) ∂T 𝖩v оны қатты денелер үшін теориялық тұрғыдан анықтау олардың ішкі энергиясының температураға байланыстылығын анықтауға келіп тіреледі. Кристал торының буындарына орналасқан бөлшектердің жалпы потенциал энергиясын Ф арқылы өрнектейік. Бұл шама теріс (Ф<0) болады да (ол тарту күштеріне негізделген) көлемнің функциясы болып табылады, яғни бөлшектердің ара қашықтықтарына байланысты: Ф=Ф(V). (1.4) Жоғарыда айтқанымыздай, кристалл бөлшектері торбуындарының айналасында тербелмелі қозғалыста болады. Мұны үш координата осьтерінің бойымен болатын тербеліс қорытындысы (қосындысы) ретінде қарастыруға болады. Сонымен кристалдағы әр бөлшектің үш еркіндік дәрежесі бар деп есептеуге болады. Жоғарыда қарастырған молекулалық (атомдық) және металдық кристалдардың бөлшектер тербелісінің энергиясын тауып көрейік. 160 140 120 100 80 60 40 20 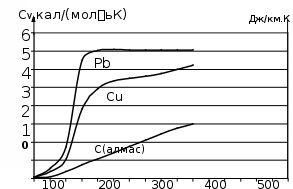 25,2 25,2 2,1 16,8 12,6 8,4 4,2 Т,К 1.3-сурет Мұндай кристалдар бөлшектерінің тербелмелі қозғалыс кезінде әрбір еркіндік дәрежесіне орташа энергияның 𝜀 мәні сәйкес келеді. Сонда торлардағы әрбір бөлшекке 3 𝜀 тең орташа энергия сәйкес келеді. Бір моль заттың тербеліс энергиясын осы бір бөлшектің орташа энергиясын NAкөбейтіп табамыз: A Um=3𝜀N (1.5) Сонымен, (1.4) және (1.5) өрнектерінің қосындысы металдық және атомдық кристалдардың ішкі энергиясын сипаттайды: U =3𝜀N + Ф(V). A (1.6) Мұндағы Ф(V)> 3N𝜀 A және (Ф< 0) ескеріп, U< 0 екенін айту қажет, міне, сондықтан бөлшектер кристалдық тордың буындарында ұсталып тұрады. Кристалдағы тербелмелі қозғалыстағы бөлшектер энергияның еркіндік дәрежелеріне қарай бірдей таралуын сипаттайтын классикалық заңға бағыналы делік. Сонда бір еркіндік дәрежесіне 𝜀 =kT тең орташа энергия сәйкес келеді. Осы мәнді (1´) қойып, NAk=R екенін ескеріп, былай жазамыз: Сонда U =3RT ∂U + Ф(V). (1.7) Cv= ∣ ∂T ∣ 𝖩v = 3R. (1.8) Егер R2 кал/ мольК немесе 8,314 Дж/ мольК екенін ескерсек, онда классикалық теория негізінде Дюлонг және Пти заңына келеміз. Бірақ классикалық теория қатты денелердің Cvтемператураға байланыстылығын қарастырмайды. Мұны кванттық теория түсіндіреді. Қатты денелердің молекула -кинетикалық теориясының негізгі ұғымдары мен түсініктері. Біз қатты дене – жер шарының бетінде, қатты денелерден салынған құрылыстарда – үйлерде өмір сүріп жатырмыз. Біздің денеміздің құрамында шамамен 65% су болғанның өзінде (мида 80%) ол қатты денеге жатады. Еңбек құралдары, машиналар да қатты денелерден жасалған. Қатты денелердің қасиеттерін білу тіршілік үшін қажет. Қатты денелер сұйықтар сияқты өзінің көлемін ғана сақтап қоймайды, сонымен бірге пішінін де сақтайды.Олар негізінен кристалл күйде болады екен. Қатты денелердің атомдары немесе молекулалары, сұйықтардікіне қарағанда, белгілі бір тепе – теңдік қалыптың маңында тербеліп тұрады. Кей кезде молекулалар өздерінің тепе – теңдік қалпын өзгертеді, бірақ бұл өте сирек болады.Сол себепті қатты денелер көлемін ғана емес, пішінін де сақтайды. Қатты денелер өздерінің физикалық қасиеттері жағынан бірінен – бірінің өте үлкен айырмашылықтары бар екі топқа, атап айтқанда: 1) кристалл денелер және 2) аморф денелер болып бөлінеді. Аморфтық денелердің физикалық қасиеттері барлық бағыттар бойынша бірдей болады. Аморфтық денелерге шыны, пластмассалар және т.б.жатады. Аморфтық денелер физикалық қасиеттерінің изотроптылығы оларды құрайтын атомдар мен молекулалардың ретсіз орналасуымен түсіндіріледі. Атомдары мен молекулалары реттелген, периодты қайталанылатын ішкі құрылымды түзе орналасатын қатты денелер кристалдар деп аталады. Кристалдық денелердің қасиеттері әртүрлі бағыттарда бірдей емес. Кристалдардың бұл қасиетін анизатроптық деп атайды. Мысалы, кристалл дененің жылулық ұлғаю коэффиценті әр түрлі бағытта түрліше болады; кристалдардың механикалық, оптикалық және электрлік қасиеттері әр түрлі бағытта бірдей болмайды. Кристалдың өзіне тән сыртқы белгісі – оның геометриялық формасының дұрыс болатындығы. Терезе шынысының бетіне су қатқанда байқалатын мұз кристалдарының геометриялық дұрыс формалары жалпыға белгілі.Кристалдардың жан - жағы айнадай жазық болып келеді, ол жазық жақтар бірімен – бірі түзу қырлар және үшкір бұрыштар жасап қиылысады. Әдетте жақтар біріне қарағанда бірі симметриялы болып орналасады. Кристалдың жазықтары белгілі бір бағытта орналасады, сындырғанда олар көбінесе осы жазықтардың бойымен жарылады. Мысалы, тас тұзының кристалдары ұрғанда өз ара перпендикуляр жазықтықтардың бойымен жарылып сынады, сонда тас тұзының кесектері параллелипипед формалы болады. Ал аморф денелердің сынған жерлері ойлы – қырлы болады; жарылып сынған шыны ұсақтарының белгілі бір формасы болмайды. Кристалл денелер монокристалдар және поликристалдар болып екіге бөлінеді. Монокристалдың басты ерекшелігі оның бүкіл көлемінде ішкі құрылымының периодты қайталануы болып табылады. Поликристалл бейберекет орналасқан кіші кристалдар жиынтығынан тұрады. Табиғатта кездесетін қатты денелердің басым көпшілігі – тас, құм, металдар, тұздар және т. б. поликристалдар болып табылады. Поликристалл дененің әрбір кіші монокристалы анизотропты, ал поликристал дене изотропты. Кристалдарды құрайтын бөлшектердің кеңістікте дұрыс кристалдық тор түзетіндігі – тәжірибеде анықталған. Кристалдық тор деп түйіндерінде кристалды құрайтын бөлшектер орналасатын кеңістіктік торды айтады. Кристалдар табандарында тек дұрыс үшбұрыш, квадрат, параллелограм және алтыбұрыш жататын әр түрлі призмалар мен пирамиданың пішінінде болады. Кристалдағы бөлшектердің периодты қайталанып орналасуын кристалл торы белгілі симметрияға ие екен дейді. Фигураның пішінінің қандай да бір дұрыстығын сипаттайтын қасиетін фигураның симметриясы дейді. Кристалдардың симметриясын жалпы түрде Е.С. Федоров қарастырған. Ол бөлшектердің кристалдарда орналасуының 230 түрі бар екенін көрсетті. Арасындағы байланысты анықтай отырып, кристалдық – химиялық анализдің методын тағайындады. Кристалдың физикалық типтері. Кристал торының түйіндерінде атомдар, иондар, молекулалар болуы мүмкін. Түйіндерде орналасқан бөлшектердің арасында белгілі күштер әсер етеді. Кристалдық тордың түйіндеріндегі бөлшектердің табиғатына және олардың арасындағы өзара әрекет күштердің қасиеттеріне қарай кристалдар төрт типке ажыратылады: атомдық, иондық, металдық және молекулалық. Атомдық кристалдар.Атомдық кристалл түйіндерінде электрлі бейтарап атомдар орналасады. Түйіндердегі атомдарды ұстап тұратын байланысты коваленттік деп атайды. Бұл байланыс тек қана атомдық кристалдарда емес, көптеген екі атомды қосындыларда кездеседі. Иондық кристалдар. Иондық кристалдың түйіндерінде әр түрлі таңбалы иондар орналасады. Олардың арасындағы әсер күштері негізінен электрлік (Кулон күштері) болып келеді Молекулалық кристалдар.Молекулалық кристалдардың түйіндерінде молекулалар орналасады. Түйіндердегі молекулаларды өзара молекулааралық күштер ұстап тұрады. Бұл күштер әлсіз, олар атомдардан молекула түзе алмайды. Молекулалық кристалдан тұратын заттар берік болмайды, олар тез буланып ұшып кетеді. Металдық кристалдар. Металдық кристалдар торының ерекшелігі – металл атомдарынан оңай бөлініп шыққан сыртқы электрондар болады. Олар газ молекулалары сияқты ретсіз қозғалып, электронды газ түзеді. Сондықтан металл кристалын барлық түйіндерінде оң иондар орналасқан электронды газдың ішіндегі тор деп қарастыруға болады. Электронды газ арқасында металдар мынадай қасиеттерге ие болады: электр және жылу өткізгіштігі өте зор; жабысқақтығы, яғни пластиктігі бар; қақтауға төзімді немесе созымдылығы үлкен. Қатты денелердің серпінділік қасиеттері. Қатты дененің өлшемдері мен көлемінің және пішінінің өзгеруін деформация деп атайды. Деформациялар қатты денелерді қыздыру мен суыту кезінде және сыртқы күштердің әсерінен пайда болады. Деформация кезінде кристалл тордың түйіндерінде орналасқан бөлшектер өздерінің тепе – теңдік қалыптарынан ығыстырылады. Осының әсерінен деформацияланған қатты денеде серпінділік күші пайда болады. Деформацияны туғызатын сыртқы күштердің әсері тоқталғаннан кейін денелердің өз өлшемдері мен пішінін және көлемін қалпына келтіру қасиеті серпінділік деп аталады. Дененің деформациясы кезінде пайда болатын және бөлшектердің ығысу бағытына қарсы бағытталған күшті Ғ Cсерпінділік күші деп аталады. Сыртқы күштердің әсері тоқталғаннан кейін жойылатын деформациялар серпінді деформациялар деп аталады. Серпінді емес деформациялар сыртқы күштердің әсері тоқталғаннан кейін жойылмайды. Мұндай деформациялар пластикалық деформациялар деп аталады. Деформацияның ең қарапайым түрлері – созылу мен сығылу. Созылу мен сығылу деформациясы Е салыстырмалы созылумен сипатталады: = ; (1.10) E llO мұндағы l=l- lO - абсолют ұзару. lO - мысалы, біліктің созылғанға дейінгі, ал l - созылғаннан кейінгі ұзындықтары. Серпінділік күш модулінің дене көлденең қимасының ауданына қатынасына тең шаманы 𝛿 механикалық кернеу деп атайды: 𝛿 = FC S ; (1.11) Халықаралық бірліктер жүйесінде механикалық кернеу бірлігіне паскаль (Па) қабылданған: 1Па = 1 Н/м2. Шамалы деформацияларда төмендегі қатынаспен анықталатын Гук заңы орындалады: 𝛿 =E𝜀 ; мұндағы Е пропорционалдық коэффициенті серпінділік модулі немесе Юнг модулі делінеді. Бір материалдан жасалған денелер үшін олардың өлшемдері мен пішініне байланыссыз серпінділік модулі бірдей: соңғы өрнектен E= 𝛿 = FSlo  𝜀 𝜀=const (1.12) 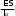 FC = l FC = l(1.13) Біліктің К қаттылық коэффициенті: K= ES lo тең болады. Практикада қатты денелердің морттық деп аталатын қасиетінің маңызы зор. Егер материал болмашы деформацияларда қирап бүлінетін болса, ол материал морт деп саналады. Мысалы: шыны, фарфор және т. б. Қатты денелердің жылулық ұлғаюы. Тәжірибеге сәйкес температура жоғарылаған сайын қатты денелердің көлемі артатындығы белгілі. Қатты денеде берілген температурада молекулалар бір – бірінен белгілі қашықтықтарда орналасады да, тепе – теңдік қалыптардың маңында тербеліс жасап тұрады. Температураның жоғарылауымен тербеліс энергиясы артады. Басқаша сөзбен айтқанда, температура артқан сайын молекулалар бір – бірінен қашықтайды. Абсолют нөлден алшақ тұрған температура аралығында көлемнің салыстырмалы өзгерісі температураның өзгерісіне пропорционал : V=𝗉T, V мұндағы 𝗉 - көлемдік ұлғаю коэффициенті, яғни 1 Кельвинге келетін көлемнің салыстырмалы өзгерісі. V=V- VO , бұнда VO - tO = OO C температураға сәйкес дененің көлемі және Т=t-t O =tдеп алсақ онда V=VO (1+𝗉t), Дененің тығыздығы үшін осыған ұқсас =O (1+𝗉t), Көлемдік жылулық ұлғаю қатты денелер мен сұйықтарға бірдей қатыста болса, сызықтық жылулық ұлғаю тек қатты денелерге ғана тән. Сызықтың жылулық ұлғаю берілген температуралық аралықта сызықтық ұлғаю коэффициентімен сипатталады: l=lO (1+𝛼 t), мұндағы lO – дененің tO = 0O C температура кезіндегі ұзындығы, l- дененің t температурадағы ұзындығы 𝛼 шамасы 1 Kельвинге келетін ұзындықтың салыстырмалы өзгерісі. Аз температура аралықтары үшін сызықтық және көлемдік ұлғаю коэффициенттерінің байланысы мына өрнекпен беріледі: 𝗉 3𝛼 , Қатты денелердің балқуы, кристалдану және сублимициясы. Қатты денелердің сұйыққа айналуы балқу деп аталады. Балқу процесінде қатты дененің кристалл торы бұзылады. Балқу процесі кезінде қатты денеге берілетін барлық жылу мөлшері кристалдық торды бұзуға және сыртқы күштерге қарсы істелетін жұмысқа жұмсалады. Балқу температурасында қатты дененің масса бірлігін сұйық күйге айналдыруға қажетті жылу мөлшерін меншікті балқу жылуы деп атайды. Заттың сұйық күйден қатты кристалдық күйге өтуі кристалдану деп аталады. Кристалдану кезінде сұйық молекулаларының қозғалысы тәртіптеледі де, кристалдық тор түйіндерінің маңыңдағы жылулық тербеністерге ауысады. Сұйықтың масса бірлігі кристалданғанда меншікті балқу жылуына тең меншікті кристалдану жылуы бөлініп шығады. Қатты денелердің булануын сублимиция деп атайды. Сублимиция кезінде молекулалар қатты дене бетінен тікелей “жұлқынып шығып” газ тәріздес күйге өтеді. Қатты денелердің жылу сыйыдылығының кванттық ұғымдары. Эйнштейн қарапайым модель ұсынды. Оның моделіне сүйенсек, әр атом жеке өзі осцилляторды құрайды және барлық кристалл атомына тең жиілікпен тербеледі. Классикалық модельден айырмашылығы кванттық осциллятордың энергиясы тек дискреттік мәндерді ғана қабылдайды. Ал осциллятордың тербеліс жиілігі болып табылады. 0 , h 0 |
