Сыйымдылыы
 Скачать 228.11 Kb. Скачать 228.11 Kb.
|
3N hvE=A 0 hv (1.14) exp∣0 ∣ - 1 kT ∣ ∣ 𝖩 Эйнштейн бойынша қатты денелердің жылусыйымдылығын (1.14)- тің Т- нан диффенциалдау арқылы аламыз hv exp∣0 ∣ dE hv ∣ kT∣ C= =3R(0 )2 𝖩 V dT kT hv 2 ∣ 𝖩 ∣exp∣0 ∣ - 1∣ (1.15) ∣ kT∣ ∣ 0 v- ді бөлшектің осцилляторының қасиетінен анықтаған болсақ, онда hv 𝜃 =0 k- деген Эйнштейн температурасы деп аталатын параметрді енгіземіз. ∣ ∣ exp 𝜃 𝜃 енгізген соң C аламыз C=3R(𝜃 )2 T𝖩 V T v 2 𝜃 ∣ exp∣ T∣ - 1∣ 𝖩 (1.16) 𝜃 << 1 болғанда жылу сыйымдылық 3R-ға ұмтылады. Қатты денелердің T көбісінде 𝜃 -та 100…300К аралығында орналасқан. Егер 𝜃 = 300К тең деп = 0 алсақ, онда v 1012 Гц тең екенін анықтай қиын емес. Эйнштейннің теориясымен эксперименттің сәйкестіргенде аңғаратынымыз: Диэлектриктердің жылу сыйымдылығының температураға байланысы нақты дәл мәлімет береді. Бірақ та функцияналдық жылу сыйымдылықтың төмен температураға байланысы эксперимент бойынша Эйнштейнмен сәйкес келмейді. Сәйкес сәздіктің бірден бір себебі қатты дененің осцилляторының жиілігі өзіндік жиілікке теңдігі. Кристалдық торда атомдардың өзара әрекеттесуінің көрінісінің келесі қадамын Дебайдың моделінен біле аламыз. Дебай бойынша кристалдың жылу сыйымдылығы Дебай атомдық кристалды тығыз орта жиынтығы ретінде және де кристалдың өлшемімен шектелген деп қарастырады. Ал олардың колективтік тербелісі әр атомның өзіндік суперпозияциялық тербелісті орта екендігін аңғартады. Ұжымдық тербеліс көп болған сайын температура төмен, ал үлкен Т атомдарда тербеліс байланысы үлкен екен. Сондықтан үлкен температурадағы Дебайдың шешімдері Эйншейнмен сәйкес. Қайтымды тербелістің ішкі энергиясын табу мәселесі Дебайдың моделімен анықталады, бұл қара дененің абсолют сәулеленудің көлемдік тығыздығын анықтау мәселесі сияқты. Кристалдардың өзіндік тығыз тербелісті бірлік спекралдық диапазонда болатын тербеліс санын анықтау қажет. Содан оны Т температура орташа энергия санын көбейтіп, тығыз тербелістің спектрлік энергия тығыздығын анықтау қажет. Бұл өлшемді кристалдарда барлық жиіліктермен интегралдау, кристалдардың ішкі энергиясын анықтауға болады. Соңғы Т дифферинциалдап, Cv-нің температурамен байланысын аламыз. Бір атомдық кристалдарға есептеулер жүргізейік, атомды кубтық тордың түйіндерінде бір- біріне а арақашықтарында орналасқан дейік. Кристалдың формасын куб деп, ал қабырғасының ұзындығын L деп алайық. Кристалдағы тығыз тербелістің өзіндік типінің есебін электромагниттік өрістегідей жүргізуге болады. Бұл екі есептің айырмашылығы кристалдағы тығыз толқындар көлденең және қима болуы мүмкін. Электромагниттік өрістік жағдайда тығыз ортада өзіндік тербелістің екуінің орнына үш түрі керек. Бұлардың жылдамдығы бір бірінен қатты аспайды. Тығыз тербелістің сандық түрін dnдеп, ал жиілік интегралын v-дан v+dv десек, 12𝑢 2 dn= dv 3 (1.17) Дебайдың болжамы бойынша тығыз тербелістің саны 3NA деп, оны кристалдық атом бос дәрежесінің саны деді. Математика бойынша мұны, 3N=L3 vmax 12𝑢v 2 dv (1.18) ∫ A 3 0 v Бұл теңдеу кристалдағы тығыз тербелістің максиамальдік жиілігін анықтайтын мүмкіндік. 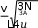 v = v =max (1.19) Оған сәйкес min минималь толқын ұзындығы мынаған тең 4𝑢 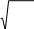 L3 3N,бұл L3 3N,бұлA өлшемнің ұқыптылығы кристалдағы атомдардың көршілермен арақашықтығын анықтайды. Бұл Дебайдың айтқанымен сай және де электромагниттік жағдайдағы кристалдардың тығыз тербелістің өзіндік түрінің орташа энергиясы Планк формуласымен анықтайды. (1.17)-ші теңдеуді орташа энергияға көбейтіп, оны 0-ден v max дейін жиіліктегі алынған туындыны бөліктеп интегралдап, кристалдың Т температурадағы ішкі энергиясын анықтаймыз, 2 vmax 12𝑢v L3 hv dv hv E= ∫ exp∣ ∣ - 1 (1.20) hv-ны 𝛼 деп белгілеп, kT 3 3 0 v 4 𝛼 3 kT𝖩 E=12𝑢hL kT max 𝛼 d𝛼 =CT (1.21) ∣ v3 ∣ h 𝖩 ∫ V 0 exp𝛼 - 1 Төмен температурада жоғары шекті шексіз деп есептесек, L 3 3 h v E=12𝑢h kT ∣∣ 4 𝛼 max ∫ 𝛼 3 d𝛼 ∣ ∣ 𝖩 0 exp𝛼 - 1 Е- мен белгіленген интеграл таблицалық болып есептеліп, 𝑢 4 15 бұл мәнді қолдана отырып, 4 L 3 k4 E= 𝑢 5 ∣ ∣ T4 (1.22) 5 v𝖩 h3 Алынған өрнекті қарапайым қылу үшін Дебайдың температурасы дегенді енгіземіз. Онда hv D 𝜃 = max k 3𝑢 4 (1.23) D A E= N 5 kT4𝜃 - 3 Е-ні Т бойынша диффенциалдасақ, онда 12𝑢 4 T 3 C = Nk∣ ∣ (1.24) V 5 A 𝜃 𝖩 Бір атомдық кристалдарда жылусыйымдылық төмен температурада Т3 пропорциясымен өзгереді. Ал жоғарғы температурада T>>𝜃Dтеңсіздігімен hvанықталады, exp hv - 1 |
| Зат | Hg | Pb | Au | Ag | Zn | Ge | Al | Si | Be | C |
| 𝜃 , D К | 60 | 94,5 | 165 | 225 | 308 | 366 | 418 | 658 | 1160 | 2000 |
1.3-кестеден Дюлонг және Птидің алмаз, берилий және т.б. заттары үшін олардың заңдарының орындалмағаны Дебайдың температуралары айтарлықтай үлкен екендігінің белгісі болды.
Дебайдың ең үлкен шегінің бірі абсолюттік нолдік температураға жақын диэлектрлік кристалдардың жылу сыйымдылығының температураға байланысын көрсетті.
140
120
100
80
60
40
20
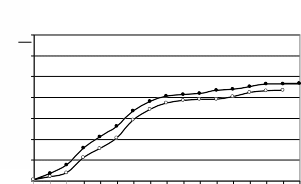 Ср
Ср Сv
