Неинерциальные системы отсчета. Неинерциальные системы отсчёта. Силы инерции при ускоренном поступательном движении системы отсчета
 Скачать 57.79 Kb. Скачать 57.79 Kb.
|
|
Неинерциальными называют такие системы отсчета, в которых не выполняются законы Ньютона. Не выполняется закон инерции, ибо в таких системах отсчета тело, на которое не действуют другие тела, не сохраняет своего состояния покоя или равномерного прямолинейного движения. Не выполняется второй закон Ньютона, так как тело может иметь ускорение, не испытывая действия со стороны другого тела. Наконец, не выполняется и третий закон Ньютона, ибо тело, испытывая действие некоторой силы инерции, не оказывает противодействия (нет тела, к которому должно быть приложено это противодействие). Различают два вида неинерциальных систем отсчета: системы, движущиеся относительно инерциальной системы отсчета поступательно с постоянным или переменным ускорением, и системы, вращающиеся с постоянной или переменной угловой скоростью относительно некоторого центра или некоторой оси. Произвольное движение системы всегда можно представить в виде суммы указанных двух движений. В НеИСО законы Ньютона в обычном виде применять нельзя, требуется введение специальных поправок — сил инерции. СИЛЫ ИНЕРЦИИ ПРИ УСКОРЕННОМ ПОСТУПАТЕЛЬНОМ ДВИЖЕНИИ СИСТЕМЫ ОТСЧЕТА Пусть в равноускоренно движущемся вагоне нитью к потолку привязан шар. 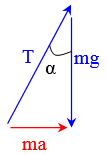 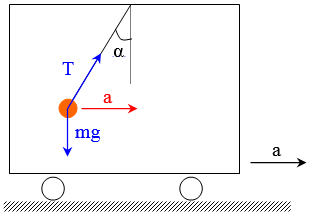 В инерциальной (лабораторной) системе отсчета второй закон Ньютона для груза имеет вид: 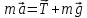 (1) (1)Угол наклона нити легко можно найти, воспользовавшись «треугольником сил», откуда tgα=a/g. Для наблюдателя в вагоне шар покоится. Его ускорение равно нулю, хотя силы, действующие на шар, направлены не вдоль одной прямой и не могут компенсировать друг друга. Сохранить уравнение (1) и в левой части закона Ньютона получить ноль можно, если перенести слагаемое 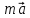 в правую часть. Тогда получим в правую часть. Тогда получим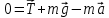 (2) (2)В правой части появилось новое слагаемое 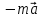 . Так как оно находится в «области сил», то и название у него — сила инерции. . Так как оно находится в «области сил», то и название у него — сила инерции.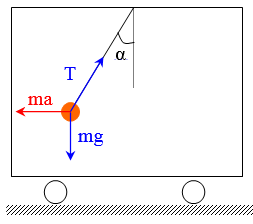 Иными словами, чтобы с точки зрения наблюдателя, находящегося в НеИСО, объяснить покой тела, мы вынуждены ввести новую силу 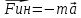 . (3). По сути, этой силы НЕТ! Она не имеет природы, и у нее нет пары по третьему закону Ньютона. Приложена сила инерции к центру масс тела, направлена против ускорения НеИСО. Для любого из тел, которые находятся в неинерциальной системе отсчета, силы инерции являются внешними; следовательно, нет замкнутых НеИСО, т. е. в неинерциальных системах отсчета не выполняются также и законы сохранения импульса, энергии и момента импульса, аккуратно надо применять законы статики. . (3). По сути, этой силы НЕТ! Она не имеет природы, и у нее нет пары по третьему закону Ньютона. Приложена сила инерции к центру масс тела, направлена против ускорения НеИСО. Для любого из тел, которые находятся в неинерциальной системе отсчета, силы инерции являются внешними; следовательно, нет замкнутых НеИСО, т. е. в неинерциальных системах отсчета не выполняются также и законы сохранения импульса, энергии и момента импульса, аккуратно надо применять законы статики.Важно, что в силе инерции m– масса тела, к которому сила приложена,  − ускорение не тела а самой НеИСО, в которую мы пересели! − ускорение не тела а самой НеИСО, в которую мы пересели! Проявление сил инерции при поступательном движении мы можем видеть в повседневных явлениях. Если поезд набирает скорость, то пассажир, сидящий при этом по ходу поезда, прижимается к спинке сиденья под действием силы инерции. Наоборот, при торможении поезда пассажир отклоняется от спинки сиденья, т. к. сила инерции направлена в противоположную сторону. Особенно силы инерции заметны при внезапном торможении поезда. Эти силы проявляются в перегрузках, возникающих при запуске и торможении космических кораблей. СИЛЫ ИНЕРЦИИ, ДЕЙСТВУЮЩИЕ НА ТЕЛО, ПОКОЯЩЕЕСЯ ВО ВРАЩАЮЩЕЙСЯ СИСТЕМЕ ОТСЧЕТА Пусть диск равномерно вращается с угловой скоростью ω (ω=const) вокруг перпендикулярной ему оси, которая проходит через его центр. На диске установлены маятники, на разных расстояниях от оси вращения и на нитях висят шарики массой m, изображенной на рис.1. Когда диск начнет вращаться, шарики отклоняются от вертикали на некоторый угол. 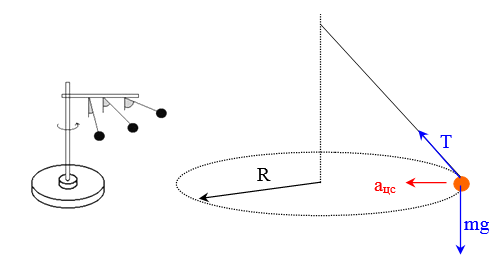 В инерциальной системе отсчета, которая связана, например, с помещением, где установлен диск, происходит равномерное вращение шарика по окружности радиусом R(расстояние от центра масс вращающегося тела до оси вращения), рис.2 Второй закон Ньютона имеет вид: 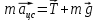 , (4) где , (4) где 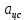 − нормальное или центростремительное ускорение. − нормальное или центростремительное ускорение.Угол отклонения нити снова можно найти из «треугольника сил»: 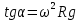 , т. е. углы отклонения нитей маятников будут тем больше, чем больше угловая скорость вращения ω и чем больше расстояние R от центра шарика до оси вращения диска. , т. е. углы отклонения нитей маятников будут тем больше, чем больше угловая скорость вращения ω и чем больше расстояние R от центра шарика до оси вращения диска.Относительно системы отсчета, которая связана с вращающимся диском, шарик покоится, что возможно, если силы 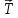 и и 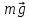 уравновешиваются силой уравновешиваются силой 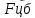 , являющейся не чем иным, как силой инерции, так как никакие другие силы на шарик не действуют. , являющейся не чем иным, как силой инерции, так как никакие другие силы на шарик не действуют.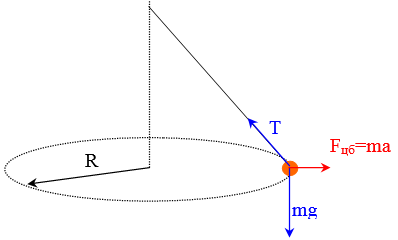 Сила 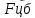 , называемая центробежной силой инерции, направлена по горизонтали от оси вращения диска и равна , называемая центробежной силой инерции, направлена по горизонтали от оси вращения диска и равна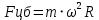 (5). (5).На практике действие центробежных сил инерции испытывают, например, пассажиры в движущемся автобусе на поворотах, летчики при выполнении фигур высшего пилотажа, дети на карусели; центробежные силы инерции используются во всех центробежных механизмах: насосах, сепараторах, в режиме отжима в стиральных машинах и т. д., где они достигают очень больших значений. При проектировании быстро вращающихся деталей машин (винтов самолетов, роторов и т. д.) используются специальные механизмы для уравновешивания центробежных сил инерции. Из формулы (5) следует, что центробежная сила инерции, которая действует на тела во вращающихся системах отсчета и которая направлена в сторону радиуса от оси вращения, зависит от угловой скорости вращения ω системы отсчета и радиуса R, но при этом не зависит от скорости тела относительно вращающихся систем отсчета. Значит, центробежная сила инерции действует во вращающихся системах отсчета на все тела, которые удалены от оси вращения на конечное расстояние, при этом не имеет значения, покоятся ли они в этой системе отсчета (как мы предполагали до сих пор) или движутся относительно нее с некоторой скоростью. Но еще раз оговоримся, что реально центробежных сил нет! Это лишь плата за выбор системы отсчета, в которой для объяснения стремления тела двигаться прямолинейно (по инерции) приходится вводить фиктивную силу. СИЛЫ КОРИОЛИСА Cила Кориолиса действует только на тела, которые движутся относительно вращающейся системы отсчета, чаще всего рассматривается случай относительно Земли. Действием этих сил объясняется ряд наблюдаемых на Земле явлений. Так, на тело, движущееся в северном полушарии на север, действует сила Кориолиса, направленная вправо по отношению к направлению движения, т. е. на восток. Если тело движется на юг, то сила Кориолиса также действует вправо, если смотреть по направлению движения, т. е. тело отклоняется на запад. Поэтому в северном полушарии наблюдается более сильное подмывание правых берегов рек; правые рельсы железнодорожных путей по движению изнашиваются быстрее, чем левые, и т. д. В южном полушарии все наоборот. Благодаря действию силы Кориолиса падающие на поверхность Земли предметы отклоняются к востоку. С силой Кориолиса связано движение маятника Фуко, которое явилось в свое время одним из доказательств вращения Земли. Если бы силы Кориолиса не было, то плоскость колебаний качающегося вблизи поверхности Земли маятника оставалась бы неизменной (относительно Земли). Действие же данной силы приводит к вращению плоскости колебаний вокруг вертикального направления. https://foxford.ru/wiki/fizika/neinertsialnye-sistemy-otschyota
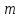 http://fini3.ru/dvizhenie-tverdogo-tela/41-dvizhenie-v-neiner.html Для любого из тел, которые находятся в неинерциальной системе отсчета, силы инерции являются внешними; следовательно, нет замкнутых НеИСО, т. е. в неинерциальных системах отсчета не выполняются также и законы сохранения импульса, энергии и момента импульса, аккуратно надо применять законы статики. http://www.terver.ru/Sila_inercii.php |

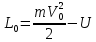 (6)
(6)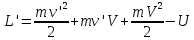 (8)
(8)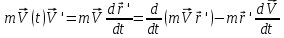 (9)
(9)
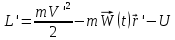 (10)
(10)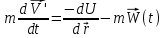 (11)
(11)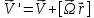 (12)
(12)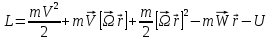 (13)
(13)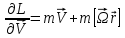 (14)
(14)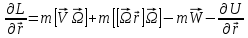 (15)
(15)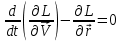 (16)
(16)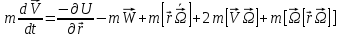 (17)
(17)