РГР по физике. ргр. Явления или процессы, рассматриваемые в данной ргр
 Скачать 86.94 Kb. Скачать 86.94 Kb.
|
|
Формулировка задания Сплошной диск вращается относительно оси, проходящей через его центр масс и перпендикулярной плоскости диска. Кинематические характеристики вращения изменяются со временем в соответствии с уравнением 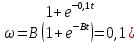 ). Построить график изменения со временем угла поворота 𝜑(𝑡), модуля угловой скорости 𝜔(𝑡) и углового ускорения 𝜀(𝑡). Для точки, находящейся на расстоянии 𝑅=0,4 м от оси вращения, определить полное ускорение и число оборотов, сделанных диском в момент времени 5 с. Значения коэффициентов в уравнениях 𝐵=0.1рад/с. Начальное условие (при t=0) ). Построить график изменения со временем угла поворота 𝜑(𝑡), модуля угловой скорости 𝜔(𝑡) и углового ускорения 𝜀(𝑡). Для точки, находящейся на расстоянии 𝑅=0,4 м от оси вращения, определить полное ускорение и число оборотов, сделанных диском в момент времени 5 с. Значения коэффициентов в уравнениях 𝐵=0.1рад/с. Начальное условие (при t=0) 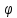 =0. Угол ворота радиуса вращения 𝜑 задан в радианах. =0. Угол ворота радиуса вращения 𝜑 задан в радианах.Теоретические основы работы Явления или процессы, рассматриваемые в данной РГР: вращательное движение твердого тела. Определения Вращательное движение – это движение, при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. Угловая скорость – это псевдовектор, характеризующий скорость вращения материальной точки вокруг центра вращения. Вектор угловой скорости определяется как первая производная от вектора угла поворота по времени: 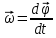 , [ , [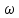 ] = ] = 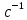 Направление вектора угловой скорости 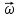 t совпадает с направлением вектора d t совпадает с направлением вектора d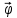 . .Угловое ускорение - физическая величина, характеризующая быстроту изменения угловой скорости материальной точки. При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости по времени: 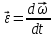 , [ , [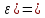 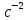 Угол поворота - это физическая величина, характеризующая поворот тела или луча, при котором одна из его точек остается неподвижной. [ 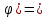 рад. рад.Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении. Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. Нормальное ускорение характеризует изменение скорости по направлению. Вектор нормального ускорения направлен по радиусу кривизны траектории.  Дано: Решение Дано: Решение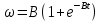 Полное ускорение а точки, движущейся по кривой линии, может Полное ускорение а точки, движущейся по кривой линии, может t = 5 c быть найдено как сумма тангенциального ускорения, направленного 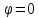 (при t=0) по касательной траектории, и нормального ускорения, направленного B = 0,1 рад/с к центру кривизны траектории: (при t=0) по касательной траектории, и нормального ускорения, направленного B = 0,1 рад/с к центру кривизны траектории: 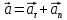 . .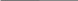 R = 0,4 м Так как векторы R = 0,4 м Так как векторы 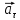 и и 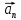 взаимно перпендикулярны, то ускорение взаимно перпендикулярны, то ускорение 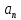 -? можно вычислить по формуле: -? можно вычислить по формуле: 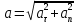 . . N-? Тангенциальное и нормальное ускорения точки вращающегося тела выражаются формулами: 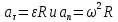 , где ω – угловая скорость тела; , где ω – угловая скорость тела; 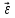 – его угловое ускорение, R – расстояние от оси вращения. – его угловое ускорение, R – расстояние от оси вращения. Угловое ускорение найдем, взяв первую производную от угловой скорости по времени: 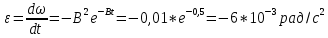 Угловую скорость найдем по заданному в условии уравнению: 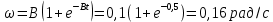 Полное ускорение тела: 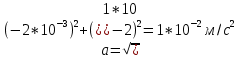 Число оборотов находится по формуле: 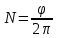 , где , где 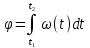 Угол поворота определим интегрированием: 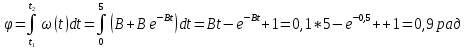 , ,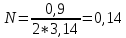 Ответ: Полное ускорение точки, находящейся на расстоянии, равном 0,4 м, от оси вращения равно приблизительно 1* 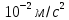 . Число оборотов, совершенных дисков в момент времени 5 с, равно приблизительно 0,14. . Число оборотов, совершенных дисков в момент времени 5 с, равно приблизительно 0,14.Графики Изменение со временем модуля угловой скорости 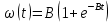  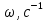   Данные для построения графика Таблица №1  t, c 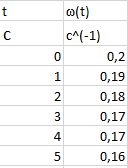 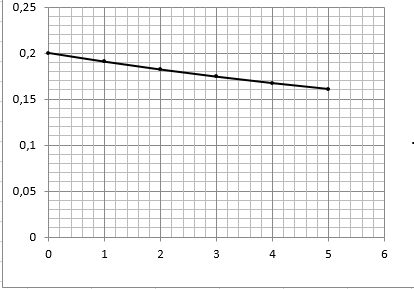 Изменение со временем угла поворота 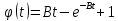     Таблица №2 Данные для построения графика 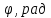 t, c 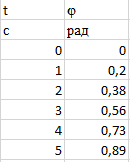 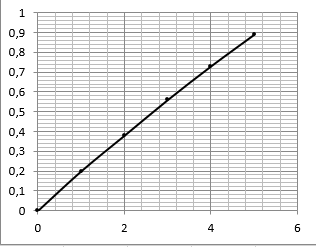 Изменение со временем модуля углового ускорения 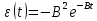  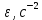    Таблица №3 Данные для построения графика t, c 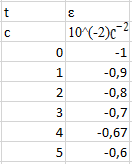 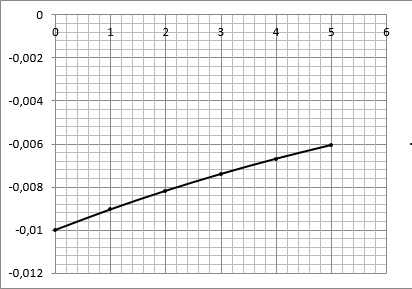 Анализ и выводы Выполняя данную расчетно-графическую работу, были определены различные значения для характеристик вращательного движения сплошного диска, такие как: полное ускорение и число оборотов, сделанных диском в момент времени t. Вращательное движение сплошного диска является неравномерным, так как происходит изменение угловой скорости со временем. Сплошной диск движется с переменным ускорением. Также были построены графики зависимости угла поворота, модуля угловой скорости и углового ускорения от времени, что позволило наиболее наглядно охарактеризовать вращательное движение сплошного диска. Модуль угловой скорости и углового ускорения со временем уменьшается, а угол поворота со временем увеличивается. |
