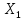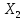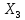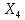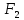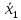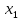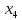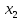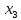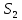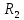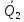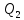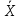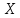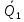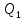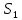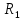КОНТРОЛЬНАЯ РАБОТУ ПО ДИСЦИПЛИНЕ ТЕОРИЯ ДИСКРЕТНЫХ УСТРОЙСТВ. КР. Синтез логической схемы включает в себя несколько этапов
 Скачать 62.19 Kb. Скачать 62.19 Kb.
|
|
ЗАДАЧА 1 Условия работы комбинационного устройства, имеющего четыре входа (X1, X2, X3, X4) и один выход F, заданы таблицей истинности (табл.1), где индекс при F соответствует номеру варианта, определяемого последней цифрой шифра студента. Требуется синтезировать функциональную логическую схему устройства в базисе И-НЕ (для четного номера варианта) и ИЛИ-НЕ (для нечетного номера варианта), применяя методы минимизации заданной логической функции с помощью алгебраических преобразований и с использованием карт Карно. Решение. Для построения функциональной логической схемы необходимо сформулировать условия ее работы и записать их в виде логической функции (ФАЛ). Синтез логической схемы включает в себя несколько этапов: 1) задание ФАЛ в виде таблицы истинности, в которой для каждого набора значений входных переменных указывают значение функции (0 или 1). Таблица истинности
2) переход от таблицы истинности к структурной формуле в базисе И, ИЛИ, НЕ; Так как количество наборов значений входных переменных, при которых значение функции равно 0, значительно превышает количество наборов, при которых функция принимает значение 1, то применяют совершенную конъюнктивную нормальную форму (СКНФ) представления ФАЛ. 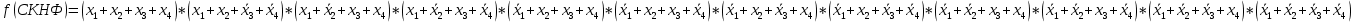 3) минимизация ФАЛ; Минимизация ФАЛ заключается в нахождении минимальных нормальных форм ее записи (МДНФ или МКНФ), имеющих минимальное число вхождений входных переменных и минимальное число термов в функции. Более удобным методом минимизации ФАЛ при числе переменных n ≤ 6 является метод карт Карно (диаграмм Вейча). Карта Карно представляет собой прямоугольник, разбитый на клетки, число которых для функции n переменных равно q=2^n, т. е. общему числу наборов значений функции (числу строк таблицы истинности), причем каждая клетка карты отличается от любой соседней, только одной инверсией одной из переменных. К  арта Карно арта Карно
Минимизация ФАЛ заключается в объединении соседних клеток (при этом клетки, лежащие на границах карты, также являются соседними по отношению друг к другу), содержащих единичные (для получения МДНФ) или нулевые (для получения МКНФ) значения, в замкнутые области. Каждая область должна представлять собой прямоугольник с числом клеток 2^n. Области могут пересекаться, и одни и те же клетки могут входить в разные области. Это позволяет исключить одну переменную при объединении двух клеток, или две переменные при объединении четырех соседних клеток, или три переменные при объединении восьми клеток карты Карно. 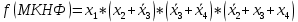 4) выбор элементной базы и запись структурной формулы, минимизированной ФАЛ в выбранном базисе (И-НЕ или ИЛИ-НЕ); Для записи полученных в результате минимизации ФАЛ в базисах И-НЕ или ИЛИ-НЕ используют закон де Моргана (закон дуальности), согласно которому инверсия дизъюнкций n переменных равна конъюнкции инверсий этих переменных и, наоборот, инверсия конъюнкции n переменных равна дизъюнкции инверсий этих переменных. Для представления функции в базисе И-НЕ необходимо произвести двойную инверсию над каждой дизъюнкций, а также двойную инверсию над все функцией и, используя закон де Моргана преобразовать инверсию дизъюнкций в конъюнкцию инверсий. 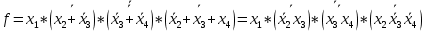 5) построение функциональной логической схемы комбинационного устройства. Для технической реализации ФАЛ используется количество логических элементов типа И-НЕ или ИЛИ-НЕ, равное числу инверсий в ее алгебраическом выражении. Так как любой из этих логических элементов должен иметь по определению число входов не менее двух, то при наличии инверсии только одной переменной, эта переменная подается на оба входа логического элемента И-НЕ или ИЛИ-НЕ в зависимости от выбранного базиса. 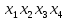               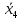 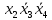    &         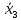         & 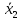       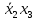       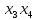     ЗАДАЧА 2 Провести синтез автомата Мили, функционирование которого описывается заданными таблицами переходов и выходов. Изобразить граф синтезируемого автомата. Задавая произвольную двоичную последовательность (входное слово), определить соответствующую двоичную выходную последовательность (выходное слово) автомата. Построить структурную схему синтезированного автомата в базисе И, ИЛИ, НЕ. Варианты таблиц переходов определяются следующим образом: по последней цифре шифра определяется последовательность восьми состояний (из четырех заданных А0, А1, А2, А3).
Эта последовательность построчно слева направо и сверху вниз заносится в таблицу переходов, состоящую из двух строк, верхняя из которых определяет последующие состояния автомата под воздействием входного сигнала x=0, а нижняя – x=1. Представить число из трех последних цифр шифра в двоичной системе счисления, добавив при необходимости слева нули до восьми разрядов или убрав (также слева) лишние, оставив восемь младших разрядов. Эта двоичная последовательность построчно слева направо и сверху вниз заносится в таблицу выходов, первая строка которой будет определять выходные сигналы автомата при воздействии входного сигнала x=0, а вторая – x=1. 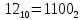
Для синтеза автомата необходимо выполнить следующее: 1) определить какая комбинация состояний триггеров будет соответствовать каждому из внутренних состояний автомата, т. е. провести кодирование внутренних состояний автомата. Затем каждой комбинации состояний триггеров нужно поставить в соответствие определенное состояние автомата. Кодирование состояний автомата может производиться различными способами. кодирования состояний автомата приведен. Кодирование состояний автомата
1   A0 A1   0  1  0 1 1  0   A3 A2  0 Рассмотрим подробнее заполнение таблицы функционирования автомата Мили. В первых трех ее столбцах записываются все возможные сочетания кодов входного сигнала и состояния автомата. Для заданного входного сигнала и состояния автомата по графу находится значение выходного сигнала, которое записывается в последнем столбце таблицы, и следующее состояние автомата, в которое он переходит. Код этого состояния заносится в четвертый и пятый столбцы таблицы. Столбцы с 6 по 9 отведены для записи сигналов управления триггерами. Управление триггерами осуществляется подачей сигналов на входы очистки (вход R) и установки (вход S). Эти сигналы для каждого триггера определяются сравнением их состояний в момент времени t - Q(t)и в последующий момент времени t+1 - Q(t+1). Например, 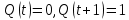 Это означает, что триггер переводится из состояния «0» в состояние «1». Для этого должен быть подан сигнал «1» на вход S и «0» на вход R «1», или Это означает, что триггер переводится из состояния «0» в состояние «1». Для этого должен быть подан сигнал «1» на вход S и «0» на вход R «1», или 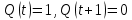 следовательно, для перевода триггера из состояния «1» в состояние «0» необходимо подать сигнал «0» на вход S и «1» на вход R. следовательно, для перевода триггера из состояния «1» в состояние «0» необходимо подать сигнал «0» на вход S и «1» на вход R.В тех случаях, когда предыдущее 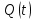 и последующее и последующее 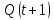 состояния триггера совпадают, (триггер хранит предыдущее состояние), то на оба входа (очистки и установки) можно подать сигнал «0» (0 S, 0 R), или на определенный вход триггера может подаваться сигнал подтверждения состояния триггера S=1, R=0 (установка «1») или S=0, R=1 (очистка или установка «0»). состояния триггера совпадают, (триггер хранит предыдущее состояние), то на оба входа (очистки и установки) можно подать сигнал «0» (0 S, 0 R), или на определенный вход триггера может подаваться сигнал подтверждения состояния триггера S=1, R=0 (установка «1») или S=0, R=1 (очистка или установка «0»).В подобных случаях, когда логический уровень сигнала управления безразличен («0» или «1»), соответствующие клетки остаются пустыми или в них заносится символ *. Таблица функционирования автомата Мили
2) синтезировать комбинационное устройство формирования сигналов управления триггерами 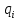 , используя таблицу переходов; , используя таблицу переходов;Для построения комбинационного устройства, формирующего сигналы управления триггерами ( 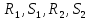 ), необходимо найти их минимальные формы, используя метод минимизирующих карт. ), необходимо найти их минимальные формы, используя метод минимизирующих карт.
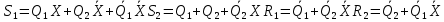 Для построения комбинационного устройства, формирующего выходной сигнал y, находят его минимальную форму, используя метод минимизирующих карт.
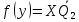 3) синтезировать комбинационное устройство, формирующее выходные сигналы автомата 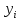 , используя таблицу выходов. , используя таблицу выходов.Используя полученные логические выражения и выбрав в качестве базиса логические элементы И, ИЛИ, НЕ, вычерчивают структурную схему синтезируемого автомата. Для обеспечения правильно работы схемы автомата необходимо предусмотреть синхронизацию его функционирования во времени. Для этого в схеме предусмотрен сигнал синхронизации C, который в моменты времени 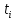 разрешает подачу управляющих сигналов с выхода комбинационного устройства на входы триггеров, выполненных по двухступенчатой схеме. Запись информации в триггеры первой ступени, образованной триггерами T 1-1 и T 2-1, происходит по высокому уровню синхросигнала, а в триггеры второй ступени (T 2-1 и T 2-2) - по низкому уровню синхросигнала. На выходе автомата y информация будет изменяться по отрицательному фронту синхросигнала C. Это соответствует алгоритму работы синхронного двухступенчатого (MS) RS-триггера. разрешает подачу управляющих сигналов с выхода комбинационного устройства на входы триггеров, выполненных по двухступенчатой схеме. Запись информации в триггеры первой ступени, образованной триггерами T 1-1 и T 2-1, происходит по высокому уровню синхросигнала, а в триггеры второй ступени (T 2-1 и T 2-2) - по низкому уровню синхросигнала. На выходе автомата y информация будет изменяться по отрицательному фронту синхросигнала C. Это соответствует алгоритму работы синхронного двухступенчатого (MS) RS-триггера.  1              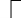  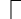     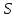 S 𝑅 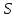 𝑅 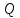 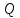 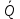 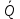 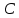 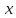       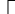 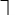 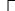     & & & & 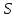 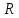 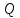 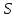 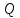 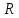 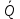 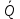 T 2-1 T 1-1 T 2-2 T 1-2           & & & & & 1 1 1 1 1 y   | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||