9опл. Тема 9 неделя ТММ. Синтез механизмов с низшими кинематическими парами

• Название: Синтез механизмов с низшими кинематическими парами
• Дата: 29.03.2023
• Размер: 414.21 Kb.
• Имя файла: Тема 9 неделя ТММ.docx
• Тип: Лекция; #1024612

Министерство образования и науки Республики Казахстан

Актюбинский региональный университет имени К.Жубанова
Факультет Технический

Кафедра Транспортная техника, организация перевозок и строительство
«Утверждаю»

Заведующий кафедрой

_______Утебаев И.С.

«___» __________ 2023 г.
ЛЕКЦИЯ 9 недели

Тема 9 недели: Тема: Синтез механизмов с низшими кинематическими парами.

Рассматриваемые вопросы: Входные и выходные параметры и этапы синтеза механизмов. Целевые функции, ограничения и дополнительные условия синтеза. Условие существования кривошипа в четырёхзвенном механизме.

Составитель: к.п.н., доцент Семенихин В.В.


Актобе, 2022

Тема 9: Синтез механизмов с низшими кинематическими парами.

(С.А. Девятериков c. 5 – 9)

9.1 Входные и выходные параметры и этапы синтеза механизмов.

Основные задачи синтеза плоских рычажных механизмов

В технике широкое распространение получили плоские рычажные механизмы. Их звенья образуют низшие вращательные или поступательные кинематические пары.

Так как в низших кинематических парах контакт звеньев происходит по поверхностям, то и удельное давление, и связанный с ним износ, меньше, чем в высших кинематических парах, что положительно сказывается на долговечности и надежности таких механизмов.

К достоинствам механизмов относятся также отсутствие дополнительных устройств, обеспечивающих постоянное замыкание кинематических пар.

Практическое их применение ограничено тем, что для воспроизводства определенной траектории отдельных точек звеньев может потребоваться многозвенный механизм. Увеличение же числа звеньев приводит к росту вероятности получения недопустимых углов передачи движения и искажения заданной зависимости вследствие погрешностей изготовления механизма.

В зависимости от назначения механизма выходные звенья механизма и их точки должны иметь определенные траектории, перемещения, скорости и ускорения. Эти величины определяются размером звеньев механизма и законом движения входного звена. Определение этих размеров, т.е. параметров кинематической схемы механизма по заданным геометрическим и кинематическим условиям движения входного звена и является основной задачей синтеза (проектирования) механизмов.

В отличие от анализа механизмов, в котором направление решения задачи однозначно определено, при синтезе возможно получение нескольких решений. Для выбора наиболее подходящего решения необходим дополнительный их анализ. Это обусловлено недостаточностью заданных условий для получения одного решения, и тем, что эти условия могут быть воспроизведены различными механизмами.

Синтез механизмов выполняется как графическими, так и аналитическими методами. Графические методы достаточно просты и наглядны, но для решения ряда задач могут не обладать требуемой точностью. Аналитические методы используются для получения решения с практически любой степенью точности. Однако следует отметить, что при воспроизведении заданных условий в пределах некоторых отклонений методы приближенного аналитического синтеза могут дать лучший результат и быстрее привести к цели, чем даже точный синтез.

Задачи синтеза механизмов весьма разнообразны, в число поставленных условий могут входить не только геометрические параметры, но и значения скоростей или ускорений, сил, моментов сил и условий их передачи между звеньями. Поэтому общих методов синтеза не существует.

Различают геометрический, кинематический и динамический синтез механизмов.

При геометрическом синтезе определяются параметры кинематической схемы механизма, исходя из положений выходного звена или траекторий (участков траекторий) отдельных точек звеньев.

При кинематическом синтезе в число исходных данных могут входить как линейные, так и угловые скорости, ускорения различных точек или звеньев механизма, а также законы их изменения.

Целью динамического синтеза является воспроизведение заданного закона движения выходного звена под действием приложенной нагрузки, а также обеспечения качественных характеристик силового взаимодействия звеньев.

9.2 Целевые функции, ограничения и дополнительные условия синтеза.
Этапы проектирования механизмов

Проектирование механизма начинается с выбора структурной схемы, которая выбирается или из уже существующих схем, или разрабатывается заново с учетом воспроизведения требуемого движения. На этом этапе необходимо приближѐнно оценить кинематические, силовые и другие характеристики будущего механизма, что не всегда возможно.

При наличии нескольких структурных схем, обеспечивающих выполнение поставленной задачи, выбирается, как правило, наиболее простая. Вопрос рационального выбора структуры механизма весьма субъективен и опирается на опыт и знания проектировщика, при этом его выбор может быть не всегда удачен.

Выбрав структурную схему, переходят к определению относительных или абсолютных размеров звеньев механизма, то есть непосредственно к синтезу механизма.

После определения геометрических параметров механизма выполняется его анализ по степени точности воспроизведения заданного движения. На основании результатов анализа делается заключение либо о достижении поставленной цели, либо о необходимости внесения изменений и уточнений в предыдущие этапы проектирования или в исходные данные. В случае если и повторные расчеты не приводят к удовлетворительным результатам, то необходимо изменить структурную схему механизма и выполнить все расчеты для нее.

Вследствие сложности и вариативности решение некоторых задач синтеза механизмов с низшими кинематическими парами найдено лишь для кривошипно-ползунного, четырехзвенного, кулисного и ряда других механизмов.

9.3 Условие существования кривошипа в четырёхзвенном механизме.

(теорема Грасгофа)

(Муйзенак с.39)

При проектировании (синтезе) четырехшарнирного механизма одним из учитываемых условий может быть проворачиваемость звеньев, т.е. наличие одного или двух кривошипов. Это зависит от соотношения длин звеньев. Например, для того, чтобы звено АВ четырехзвенника (рис. 2.13) могло стать кривошипом, оно должно последовательно пройти через два крайних положения. Используя три положения механизма, получаем следующие условия: для положений 1, 2, 3, предварительно обозначив длины звеньев: l_AB a, l_BC = b, l_CD = c, l_AD = d.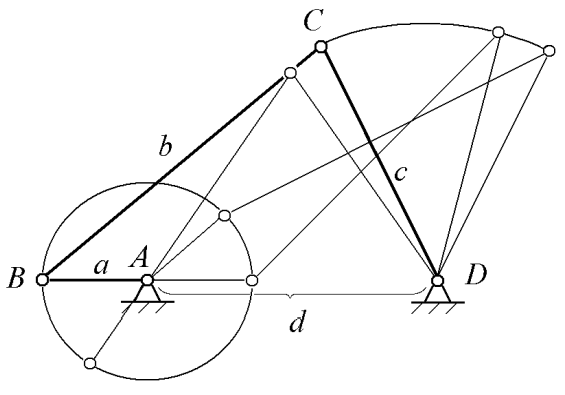



Рис. 2.13. К условию проворачиваемости кривошипа в шарнирном четырехзвеннике



рис.37 (Из Недоводеева с.31)
При этом a + d  b + c – положение 1;

а + b  d + c – положение 2;

c  b + d – a или a + с  b + d – положение 3 (см. рис. 2.13), т.е. сумма длин кривошипа и любого другого звена меньше суммы остальных звеньев. Сложим попарно полученные неравенства и получим: а  с; а  d; a  b, т.е. кривошип является самым коротким звеном. Если данные условия не выполняются, то механизм будет либо двухкривошипным, либо двухкоромысловым. Эти условия используются при геометрическом синтезе.
(С.А. Девятериков c. 5 – 9)

Решая задачу синтеза плоского четырехзвенного механизма, необходимо определить, могут ли какие-либо из его звеньев за цикл работы совершать полный оборот, то есть являться кривошипами. Наличие в таких механизмах одного или двух кривошипов, или же их отсутствие зависит от соотношения длин звеньев. Рассмотрим шарнирный четырехзвенник OABC (рис. 1), длины звеньев которого равны a, b, c и d . Если звено OA является кривошипом, то при работе оно должно занимать и крайнее правое OA₁) , и крайнее левое  OA₂) положения. Пусть длина самого короткого звена равна a , а самого длинного – d . Рассмотрим треугольники A₁В₁С и A₂В₂С. С учетом того, что сумма двух сторон в треугольнике всегда больше его третьей стороны, можно записать следующие неравенства:

d  a < b  c; (1)

d  a < b  c . (2)

Вне зависимости от длин b и c неравенство (1) всегда обеспечит выполнение неравенства (2). Если же самым длинным звеном является звено AВ b > c > d или BC c > b > d , то неравенство (2) только усиливается. Согласно рисунку 1 звено BC не делает полного оборота вокруг стойки, то есть является коромыслом, а звено AВ, не связанное со стойкой – шатуном.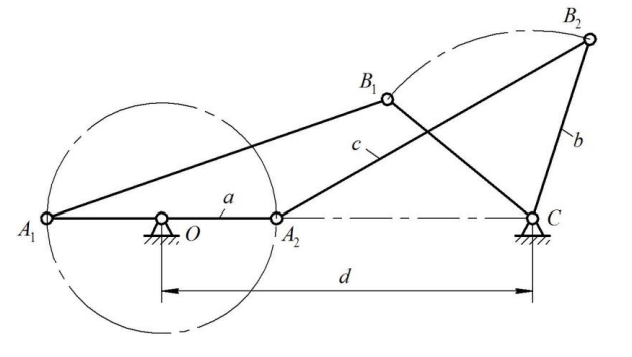



Рис. 1. Шарнирный четырехзвенник
Именно неравенство (1) определяет условие проворачиваемости звена (условие существования кривошипа).

Это условие называют также теоремой Грасгофа: самое короткое звено шарнирного четырехзвенника может быть кривошипом, если сумма длин самого короткого и самого длинного звеньев меньше суммы длин остальных звеньев механизма.

Франц Грасгоф (11.07.1826 – 26.10.1893) – немецкий механик и машиностроитель, один из основателей «Общества немецких инженеров», почетный доктор Ростоцкого университета, профессор кафедры прикладной механики и теории машин Политехникума Карлсруэ. Известен работами по кинематике механизмов, теории упругости и машиноведению (теория кинематических пар и кинематических цепей).

Используя эту теорему, шарнирные четырехзвенники можно разбить на три вида:

– в кривошипно-коромысловом механизме (рис. 1) за стойку принимается звено, расположенное рядом с самым коротким;

- в двухкривошипном механизме сумма длин самого короткого и самого длинного звеньев меньше суммы длин остальных звеньев, а за стойку принято самое короткое звено;

– в двухкормысловом механизме (рис. 2) либо длины звеньев не удовлетворяют условию (1), либо условие (1) выполняется, но самым кротким звеном является шатун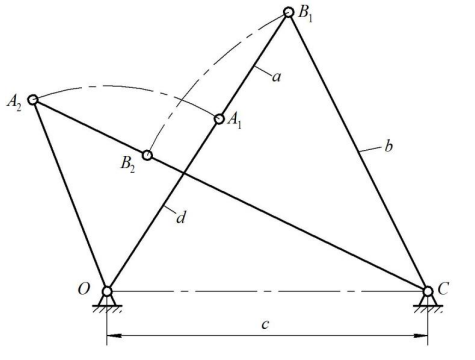



Рис. 2. Двухкоромысловый механизм
Если неравенство (1) превратится в равенство d  a  b  c , то все звенья механизма в одном из крайних положений будут расположены на одной прямой, что приводит к неопределенности движения выходного звена (оно может двигаться в двух направлениях). Во внецентренном кривошиппно-ползунном механизме (рис.3) звено OA является кривошипом, если при вращении проходит через положения ОA₁ и ОA₂ , соответствующие крайним положениям ползуна В₁ и В₂ , что возможно при выполнении условия

l₁ 2 - |e|.

где e – внеосность (дезаксиал). Штриховой линией на рис. 3 показан механизм с отрицательным дезаксиалом e < 0.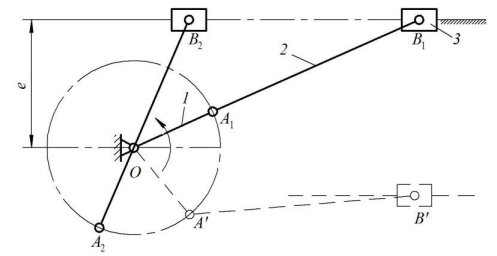


Рис.3. Внецентренный кривошиппно-ползунный механизм
Если выполняется условие l₁>l₂  |e|, то звено OA превращается в коромысло, а механизм становится коромыслово-ползунным.
Вопросы для закрепления

1. Перечислите основные этапы синтеза плоских механизмов с низшими парами.

2. Сформулируйте условия существования кривошипа в плоских четырехзвенных механизмах.

3. Дайте определение направляющего механизма. Приведите пример.

4. Дайте определение передаточного механизма. Приведите пример.

5. Как осуществляется синтез соосного кривошипно-ползунного механизма по средней скорости ползуна?

6. Как осуществляется синтез четырехзвенных механизмов по двум положениям?

7. Как осуществляется синтез четырехзвенных механизмов по трем положениям?

8. Как осуществляется синтез кулисного механизма (с качающейся кулисой) по заданному ходу выходного звена и коэффициенту изменения его средней скорости?

Самое короткое звено шарнирного четырехзвенника может быть кривошипом, если сумма длин самого короткого и самого длинного звеньев меньше суммы длин остальных звеньев. Это положение носит название правила Грасгофа

Применяя это правило, шарнирные четырехзвенники разбивают на три группы:

1) механизм будет кривошипно-коромысловым (рис. 4.4), если за стойку принято звено, расположенное рядом с самым коротким;

2) механизм будет двухкривошипным, если сумма длин самого короткого и самого длинного звеньев менше суммы длин остальных звеньев и за стойку принято самое короткое его звено; это следует из того, что, если кривошип при выполнении правила Грасгофа делает полный оборот относительно стойки и шатуна, то и эти звенья совершают полный оборот относительно кривошипа;

3) механизм будет двухкоромысловым, если размеры его звеньев не удовлетворяют правилу, а также в том случае, когда сумма длин самого короткого и самого длинного звеньев меньше суммы длин остальных звеньев, но самое короткое его звено является шатуном (рис. 4.4, б), и, следовательно, возможность быть ему кривошипом отпадает, потому что оно не является звеном, расположенным рядом со стойкой. В предельном случае, когда неравенство (4.1) превращается в равенство, все звенья механизма в одном из крайних положений располагаются по одной прямой. В результате получится неопределенность движения выходного звена (оно сможет двигаться либо в одном, либо в другом направлении)