Система нормативных документов в строительстве России и стран СНГ
 Скачать 2.1 Mb.
|
|
4. Расчётные факторы Это нагрузки и механические характеристики материалов (бетона и арматуры). Они обладают статистической изменчивостью или разбросом значений. В расчётах по предельным состояниям учитывают (в неявной форме) изменчивость нагрузок и механических характеристик материалов, а также различные неблагоприятные или благоприятные условия работы бетона и арматуры, условия изготовления и эксплуатации элементов зданий и сооружений. Нагрузки, механические характеристики материалов и расчётные коэффициенты нормированы. При проектировании железобетонных конструкций значения нагрузок, сопротивлений бетона и арматуры устанавливают по главам СНиП 2.01.07-85* и СП 52-101-2003. 5. Классификация нагрузок. Нормативные и расчётные нагрузки Нагрузки и воздействия на здания и сооружения в зависимости от продолжительности их действия делят на постоянные и временные. Последние, в свою очередь, подразделяются на длительные, кратковременные и особые. Постоянными нагрузками являются вес несущих и ограждающих конструкций зданий и сооружений, вес и давление грунтов, воздействие предварительного напряжения железобетонных конструкций. К временным длительным нагрузкам относятся: вес стационарного оборудования на перекрытиях — станков, аппаратов, двигателей, ёмкостей и т. п.; давление газов, жидкостей, сыпучих тел в ёмкостях; нагрузки на перекрытия от складируемых материалов и стеллажного оборудования в складских помещениях, холодильниках, зернохранилищах, книгохранилищах, архивах и подобных помещениях; температурные технологические воздействия от стационарного оборудования; вес слоя воды на водонаполненных плоских покрытиях и др. К временным кратковременным нагрузкам относятся: вес людей, ремонтных материалов в зонах обслуживания и ремонта оборудования, снеговые нагрузки с полным нормативным значением, ветровые нагрузки, нагрузки, возникающие при изготовлении, перевозке и монтаже элементов конструкций и некоторые др. К особым нагрузкам относятся: сейсмические и взрывные воздействия; нагрузки, вызываемые резкими нарушениями технологического процесса, временной неисправностью или поломкой оборудования и т. п. Нагрузки в соответствии со СНиП 2.01.07-85* делятся также на нормативные и расчётные. Нормативными называются нагрузки или воздействия близкие по величине к наибольшим возможным при нормальной эксплуатации зданий и сооружений. Их значения приводятся в нормах. Изменчивость нагрузок в неблагоприятную сторону оценивают коэффициентом надёжности по нагрузке γf. Расчётное значение нагрузки gдля расчёта конструкции на прочность или устойчивость определяется путём умножения её нормативного значения gпна коэффициент γf, обычно больший 1  Значения  дифференцированы в зависимости от характера нагрузок и их величины. Так, например, при учёте собственного веса бетонных и железобетонных конструкций = 1,1; при учёте собственного веса различных стяжек, засыпок, утеплителей, выполняемых в заводских условиях, = 1,2, а на строительной площадке =1,3. Коэффициенты надёжности по нагрузке для равномерно распределённых нагрузок следует принимать:1,3 — при полном нормативном значении менее 2 кПа (2 кН/м2); 1,2 — при полном нормативном значении 2 кПа (2 кН/м2) и более. Коэффициент надёжности по нагрузке для собственного веса при расчёте конструкции на устойчивость положения против всплытия, опрокидывания и скольжения, а также в других случаях, когда уменьшение массы ухудшает условия работы конструкции, принимают равным 0,9.Расчёты по предельным состояниям второй группы ведут по нормативным нагрузкам или по расчётным, взятым с γf= 1. Здания и сооружения подвергаются одновременному действию различных нагрузок. Поэтому расчёт здания или сооружения в целом, либо отдельных его элементов, должен выполняться с учётом наиболее неблагоприятных сочетаний этих нагрузок или усилий, вызванных ими. Неблагоприятные, но реально возможные сочетания нагрузок при проектировании выбираются в соответствии с рекомендациями СНиП 2.01.07-85*. В зависимости от состава учитываемых нагрузок различают сочетания: основные, включающие постоянные, длительные и кратковременные нагрузки Т = ΣТпост + ψ1 ΣТдлит + ψ2 ΣТкрат, где Т = М, Т, Q; ψ – коэффициент сочетаний (если учитывается 1 кратковременная нагрузка, то ψ1 = ψ2 =1,0, если в сочетание входят 2 и более кратковременных нагрузок, то ψ1 = 0,95, ψ2= 0,9); особые, включающие дополнительно к постоянным, длительным и кратковременным нагрузкам особую нагрузку (ψ1 = 0,95, ψ2 = 0,80). 22. Определение нагрузок и воздействий. Постоянные нагрузки и воздействия в случае невыгодных сочетаний этих конструкций. Понятие о грузовой площадке. СНиП приводит 6 постоянных нагрузок и воздействий: № 1 - № 6. Нагрузка № 1 называется собственный вес конструкции.Эта нагрузка всегда действует; не учитывается только, когда она пренебрежительно мала по отношению к другим нагрузкам. Она вертикальна – направлена сверху вниз, постоянная. Определяется путем взвешивания по табличным данным, по графикам, номограммам, формулам и путем расчета по проектным объемам. Последний метод – самый распространенный при проектировании инженерных сооружений, причем могут использоваться и указанные выше способы. Нагрузка – от собственного веса конструкции. N=۷.ﻻ Для сложных конструкций необходима разбивка их на элементарные объемы. Например, подсчитаем нагрузку от собственного веса (расчетную) одного квадратного метра ездового полотна городского путепровода. Задаемся типом покрытия – асфальтобетон. Защитный слой – из цементобетона (4 см). Гидроизоляция – 1 см. Выравнивающий слой – 3 см. Определяем объем каждого слоя: Vпокр. = 1 .1 .0,07 = 0,07 м3 ﻻ покр. = 2,3 т/м3 ﻻ ж/б = 2,5 т/м3 ﻻ гидроиз. = 1,5 т/м3 ﻻ защ. = 2,2 Нормативное значение нагрузки – N N = Vпок. ﻻ пок + Vзащ. ﻻ защ + Vгид. ﻻ гидроиз + Vвырав. ﻻ вырав. Расчетное значение определяется путем умножения нормативной нагрузки на свое соответствующее значение коэффициента надежности ﻻf ﻻf покрытия сооружений в городских условиях = 2,0, для остальных слоев ﻻf = 1,3. 23. Расчет реальных конструкций и их элементов является либо теоретически невозможным, либо практически неприемлемым по своей сложности. Поэтому в сопротивлении материалов применяется модель идеализированного деформируемого тела, включающая следующие допущения и упрощения:
Эти положения ограниченно применимы к решению конкретных задач. Например, для решения задач устойчивости утверждения 4-6 не справедливы, утверждение 3 справедливо не всегда. Теории прочности Прочность конструкций определяется с использованием теории разрушения — науки о прогнозировании условий, при которых твердые материалы разрушаются под действием внешних нагрузок. Материалы, как правило, подразделяются на разрушающиеся хрупко и пластично. В зависимости от условий (температуры, распределения напряжений, вида нагрузки и т. п.) большинство материалов может быть отнесено к хрупким, пластичным или обоим видам одновременно. Тем не менее, для большинства практических ситуаций, материалы могут быть классифицированы как хрупкие или пластичные. Несмотря на то, что теория разрушения находится в разработке уже более 200 лет, уровень её приемлемости для механики сплошных сред не всегда достаточен. Математически теория разрушения выражается в виде различных критериев разрушения, справедливых для конкретных материалов. Критерием разрушения является поверхность разрушения, выраженная через напряжения или деформации. Поверхность разрушения разделяет «поврежденное» и «не поврежденное» состояния. Для «поврежденного» состояния трудно дать точное физическое определение, это понятие следует рассматривать как рабочее определение, используемое в инженерном сообществе. Термин «поверхность разрушения», используемый в теории прочности, не следует путать с аналогичным термином, который определяет физическую границу между поврежденными и не поврежденными частями тела. Довольно часто феноменологические критерии разрушения одного и того же вида используются для прогнозирования хрупкого и пластичного разрушения. Среди феноменологических теорий прочности наиболее известными являются следующие теории, которые принято называть «классическими» теориями прочности:
Классические теории прочности имеют существенные ограничения для их применения. Так теории наибольших нормальных напряжений и наибольших деформаций применимы лишь для расчета прочности хрупких материалов, причём только для некоторых определённых условий нагружения. Поэтому эти теории прочности сегодня применяют весьма ограниченно. Из перечисленных теорий наиболее часто используют теорию Мора, которую также называют критерием Мора-Кулона. Кулон(Coulomb) в 1781 г. на основе выполненных им испытаний установил закон сухого трения, который использовал для расчета устойчивости подпорных стенок. Математическая формулировка закона Кулона совпадает с теорией Мора, если в ней выразить главные напряжения через касательные и нормальные напряжения на площадке среза. Достоинством теории Мора является то, что она применима к материалам, имеющим разные сопротивления сжатию и растяжению, а недостатком то, что она учитывает влияние только двух главных напряжений — максимального и минимального. Поэтому теория Мора не точно оценивает прочность при трехосном напряженном состоянии, когда необходимо учитывать все три главных напряжения. Кроме того, при использовании эта теория не учитывается поперечное расширение (дилатацию) материала при сдвиге. На эти недостатки теории Мора неоднократно обращал внимание А. А. Гвоздев, который доказал неприменимость теории Мора для бетона.[1] На смену «классическим» теориям прочности в современной практике пришли многочисленные новые теории разрушения. Большинство из них используют различные комбинации инвариантов тензора напряжений Коши (Cauchy) Среди них наиболее известны следующие критерии разрушения: Друкера-Прагера (Drucker-Prager). Бреслера-Пистера (Bresler-Pister) — для бетона. Вильяма-Варнке (Willam-Warnke) — для бетона. Хенкинсона (Hankinson)- эмпирический критерий, используемый для ортотропных материалов типа древесины. Хила (Hill) — для анизотропных тел. критерий Tsai-Wu — для анизотропных материалов. критерий Hoek-Brown -для скальных массивов. Перечисленные критерии прочности предназначены для расчета прочности однородных (гомогенных) материалов. Некоторые из них используются для расчёта анизотропных материалов. Для расчета прочности неоднородных (не гомогенных) материалов используется два подхода, называемые макро-моделированием и микро-моделированием. Оба подхода ориентированы на использование метода конечных элементов и вычислительной техники. При макро-моделировании предварительно выполняетсягомогенизация — условная замена неоднородного (гетерогенного) материала на однородный (гомогенный). При микро-моделировании компоненты материала рассматриваются с учётом их физических характеристик. Микро-моделирование используют в основном в исследовательских целях, так как расчет реальных конструкций требует чрезмерно больших затрат машинного времени. Методы гомогенизации широко используются для расчета прочности каменных конструкций, в первую очередь для расчета стен-диафрагм жесткости зданий. Критерии разрушения каменных конструкций учитывают многообразные формы разрушения каменной кладки. Поэтому поверхность разрушения, как правило. принимается в виде нескольких пересекающихся поверхностей, которые могут иметь разную геометрическую форму. Применение Методы сопротивления материалов широко используются при расчете несущих конструкций зданий и сооружений, в дисциплинах связанных с проектированиемдеталей машин и механизмов. Как правило, именно из-за оценочного характера результатов, получаемых с помощью математических моделей этой дисциплины, при проектировании реальных конструкций все прочностные характеристики материалов и изделий выбираются с существенным запасом (в несколько раз относительно результата, полученного при расчетах). 26. Коэффициент вариации случайной величины — мера относительного разброса случайной величины; показывает, какую долю среднего значения этой величины составляет её средний разброс. Исчисляется в процентах. Вычисляется только для количественных данных. В отличие от среднего квадратического или стандартного отклонения измеряет не абсолютную, а относительную меру разброса значений признака в статистической совокупности. По мнению автора рассматриваемого коэффициента К. Пирсона — коэффициент вариации эффективнее абсолютного показателя вариации[3]. Известно, что коэффициент вариации может быть записан посредством долей[4]:  где 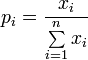 . где  — математическое ожидание. Эта формула применяется для вероятностных моделей.КОЭФФИЦИЕНТ ИЗМЕНЧИВОСТИ ВЫБОРКИ —  ,где m2 — второй выборочный момент, x — выборочное среднее. Характеризует изменчивость изучаемого признака. Широко используется при оценке ошибок подсчетов. Коэффициент надежности установленный нормами расчета коэффициент, учитывающий возможность отклонения нагрузки (коэффициент надежности по нагрузке) или прочности материала (коэффициент надежности по материалу) от нормативных их значений, приводится в СНиП. Для примера –коэффициенты надежности по нагрузкам.  27. Расчётная схема сооружения — в строительной механике, упрощённое изображение сооружения, принимаемое для расчёта. Различают несколько видов расчётных схем, отличающихся основными гипотезами, положенными в основу расчёта, а также используемым при расчёте математическим аппаратом. Чем точнее расчётная схема соответствует действительному сооружению, тем более трудоёмок его расчёт. Расчётная схема состоит из условных элементов: стержней, пластин, оболочек, массивов и связей. Стержни используют в расчётных схемах стержневых конструкций (стоек, балок, арок и др.), систем из таких конструкций (ферм, рам, сетчатых оболочек), а также для приближённого расчёта плоскостных конструкций (например, несущих стен зданий). Пластины треугольной и прямоугольной формы являются основными конечными элементами при расчёте методом конечных элементов плоскостных конструкций (стен и плит перекрытий зданий). Оболочки являются расчётной схемой различных пространственных конструкций (куполов, сводов, оболочек). Массивы в расчётных схемах используются, как правило, в качестве недеформируемых опор пролётных конструкций, опирающихся на сжимаемое основание. Связи в расчётных схемах соединяют между собой отдельные элементы, а также конструкцию с основанием. В расчётных схемах связи различаются по числу степеней свободы, которые они отнимают от системы. Связи могут быть дискретные и распределённые (континуальные). Стержни и пластины, соединённые распределёнными связями называются составными стержнями и пластинами. [1] |