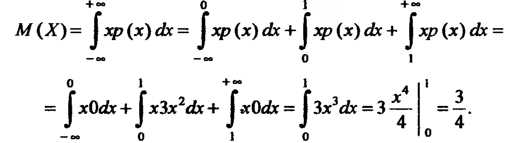Система нормативных документов в строительстве России и стран СНГ
 Скачать 2.1 Mb.
|
|
Расчётные схемы многоэтажных зданий Многоэтажное здание является сложной пространственной системой, которая в зависимости от этажности, особенностей конструктивной системы и действующих нагрузок, рассчитывается с разной степенью детализации с использованием различных расчётных схем. В современной практике проектирования расчёт здания, как правило, выполняется по специальным программам с применением вычислительной техники. [2] [3] При одномерной расчётной схеме здание рассматривается как консольный тонкостенный стержень или система стержней, упруго или жёстко закреплённых в основании. Предполагается, что поперечный контур стержня или системы стержней неизменяем. При двухмерной расчётной схеме здание рассматривается как плоская конструкция, способная воспринимать только такую внешнюю нагрузку, которая действует в её плоскости. Для определения усилий в вертикальных несущих конструкциях условно принимается, что все они расположены в одной плоскости и имеют одинаковые горизонтальные перемещения в уровне перекрытий. При трёхмерной расчётной схеме здание рассматривается как пространственная система, способная воспринимать приложенную к ней пространственную систему нагрузок. 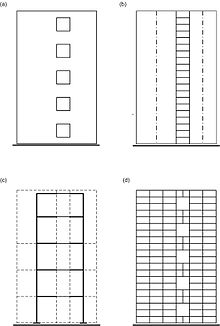 Двухмерные расчётные схемы стены с регулярно расположенными по вертикали проёмами (a): составной стержнь (b); многоэтажная рама (c); пластинчатая система МКЭ (d) В дискретных расчётных схемах неизвестные усилия или перемещения определяют для конечного количества узлов системы путём решения систем алгебраических уравнений. Дискретные расчётные схемы наиболее приспособлены для расчёта методом конечных элементов. Такие схемы широко используют для моделирования не только стержневых систем, но и сплошных пластин и оболочек. В дискретно-континуальных расчётных схемах неизвестные силовые факторы или перемещения задают в виде непрерывных функций вдоль одной из координатных осей. Неизвестные функции определяются решением краевой задачи для системы обыкновенных дифференциальных уравнений. В теории составных стержней принимается, что стержни деформируются только от продольных сил и изгиба. Между тем вертикальные диафрагмы жесткости многоэтажных зданий часто имеют такие соотношения размеров в плане и по высоте здания, для которых необходимо учитывать деформации сдвига. 28. Чтобы обеспечить безопасные условия эксплуатации зданий и сооружений, производят расчет конструкций. Строительные конструкции рассчитывают в два этапа: 1) статический (или динамический) расчет, который заключается в составлении расчетных схем, наиболее близко отвечающих работе конструкции в реальных условиях и определении внутренних усилий (изгибающих моментов М, поперечных Q и продольных N сил и др.) в опасных сечениях проектируемых конструкций. Этот расчет производится по формулам сопротивления материалов и общим правилам строительной механики; 2) конструктивный расчет - выбор материала, рациональных форм и размеров сечения, марок и класса материала (камня, бетона), класса стали, породы и качества древесины и т.д. Известны три метода конструктивного расчета: 1) по допускаемым напряжениям; 2) по разрушающим нагрузкам; З) по предельным состояниям Проектировщики применяют третий метод расчета. Цель такого расчета - не допускать предельных состояний при эксплуатации в течение всего срока службы конструкции, здания или сооружения. Расчет выполняют исходя из того, чтобы значения усилий, напряжений, деформаций, перемещений не превышали предельных значений, устанавливаемых СНиП. Значения нагрузок, действующих на конструкции, прочностные характеристики материалов, из которых они сделаны, и условия их эксплуатации обладают определенной изменчивостью и могут отличаться от установленных нормами. В расчете по методу предельных состояний это учитывается введением ряда коэффициентов перегрузки n, условий работы mв, надежности и др. Числовые значения этих коэффициентов приводятся в СНиП. Любая задача расчета конструкций имеет три стороны: статическую (или динамическую), геометрическую и физическую. Статическая (динамическая) сторона задачи заключается в установлении связи между внешними нагрузками, действующими на конструкцию, и внутренними усилиями в любом ее сечении, которая определяется условиями статического (динамического) равновесия. Поскольку внутренние усилия заранее неизвестны, приходится привлекать геометрические и физические соотношения. Геометрические соотношения связывают перемещения и деформации конструкции. Физические определяют закон, по которому напряжения зависят от деформаций. 31.Основными причинами, приводящими к авариям строительных конструкций, являются: ошибки при проектировании; недостаточный технический надзор и контроль качества при изготовлении и монтаже; нарушение правил эксплуатации зданий и сооружений; несовершенство норм и технических условий; ошибки в выдаче исходных данных для проектирования. Указанные ошибки могут привести к внезапному отказу (аварии) или постепенному отказу (аварийному состоянию) сооружения. 29.Воздействие агрессивной окружающей среды на строительные конструкции при эксплуатации может привести к коррозии бетона, арматуры, закладных деталей, а также к преждевременному износу каменных и бетонных конструкций, может вызвать разрушение и гниение деревянных элементов и как следствие — снижение несущей способности конструкций здания в целом. Поэтому при эксплуатации зданий необходимо определить участки коррозионного повреждения бетона, арматуры, характер и степень этих повреждений, а также установить степень износа каменных конструкций и т.д. В процессе эксплуатации необходимо обеспечивать достаточную вентиляцию помещений для удаления агрессивных газов, защищать элементы зданий от увлажнения атмосферными осадками и грунтовыми водами, повышать коррозионную стойкость бетонных и железобетонных конструкций путем поверхностной и объемной обработки поверхностно-активными веществами, устраивать антикоррозионные покрытия. 32.Надежность- сложное свойство, которое, в зависимости от назначения объекта и условий его применения, характеризуется безотказностью, долговечностью, ремонтопригодностью и сохраняемостью. Главным показателем надежности несущей конструкции является безопасная ее работа под действием внешних нагрузок и различных воздействий возникающих при эксплуатации( температурных, коррозионных, сейсмических и др.) Безопасность – свойство, показывающее возможность объекта непрерывно сохранять работоспособное состояние в течении заданного времени. Долговечность – свойство объекта сохранять работоспособное состояние до наступления предельного состояние при установленной системе технического обслуживания и ремонта. Ремонтопригодность – свойство объекта, заключающееся в приспособленности к предупреждению и обнаружению причин возникновения отказов, повреждений, а также поддержанию и восстановлению работоспособности проведением технического обслуживания и ремонтов. Количество ремонтопригодности определяется затратами времени, труда и средств. Ремонтопригодность определяет доступность, контролепригодность, агрегатирование, легкосъемность, унификацию и тд. Сохраняемость – свойство объекта сохранять значения показателей безотказности, долговечности и ремонтопригодности в течение хранения и после него и ( или ) транспортирования. Наиболее эффективные методы повышения сохраняемости – консервация, применение специальных защитных покрытий и пропитывающих составов, профилактическое обслуживание хранящихся объектов, повышение транспортабельности объектов, защита от старения полимеров. 30.Плотность распределения прочности материала 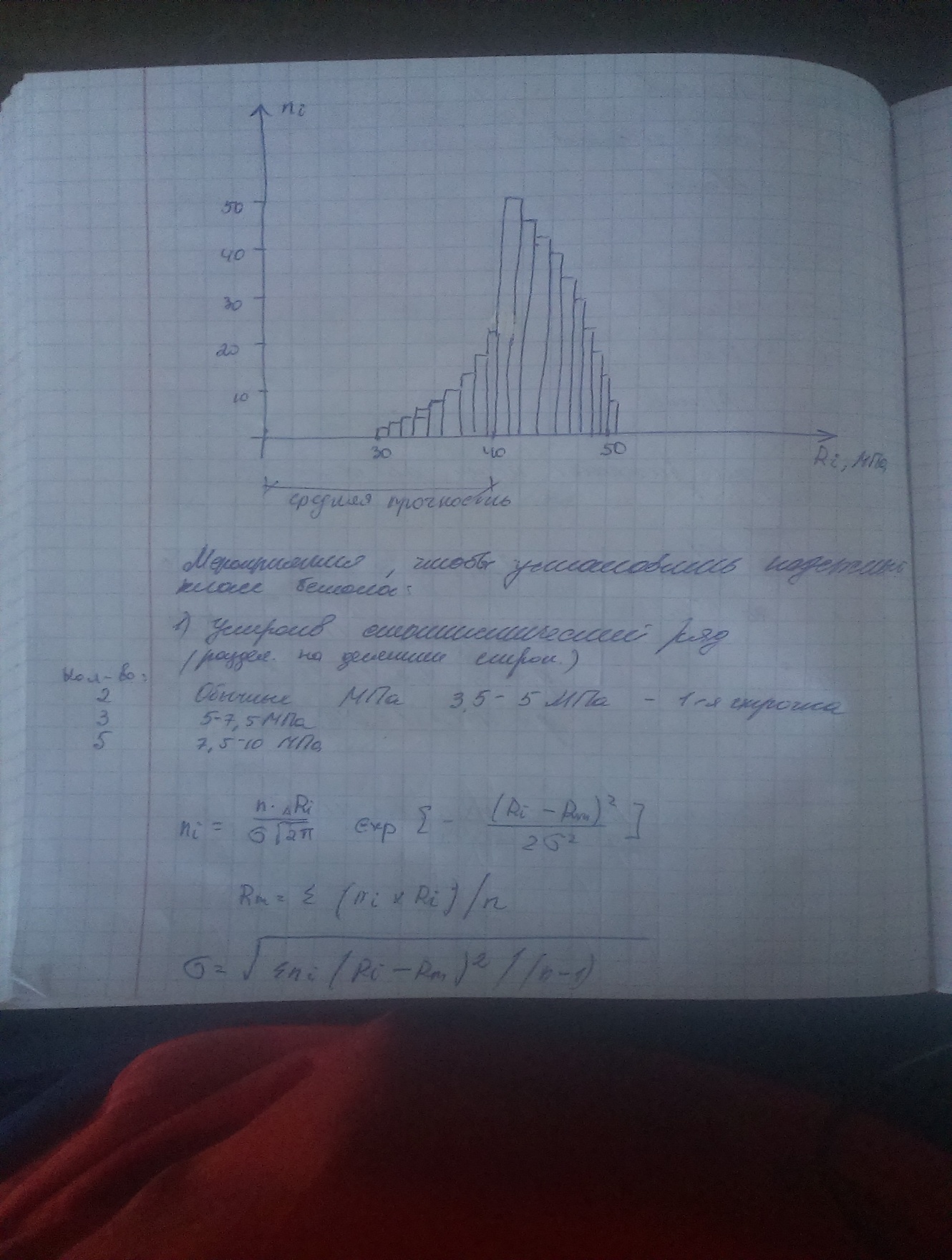 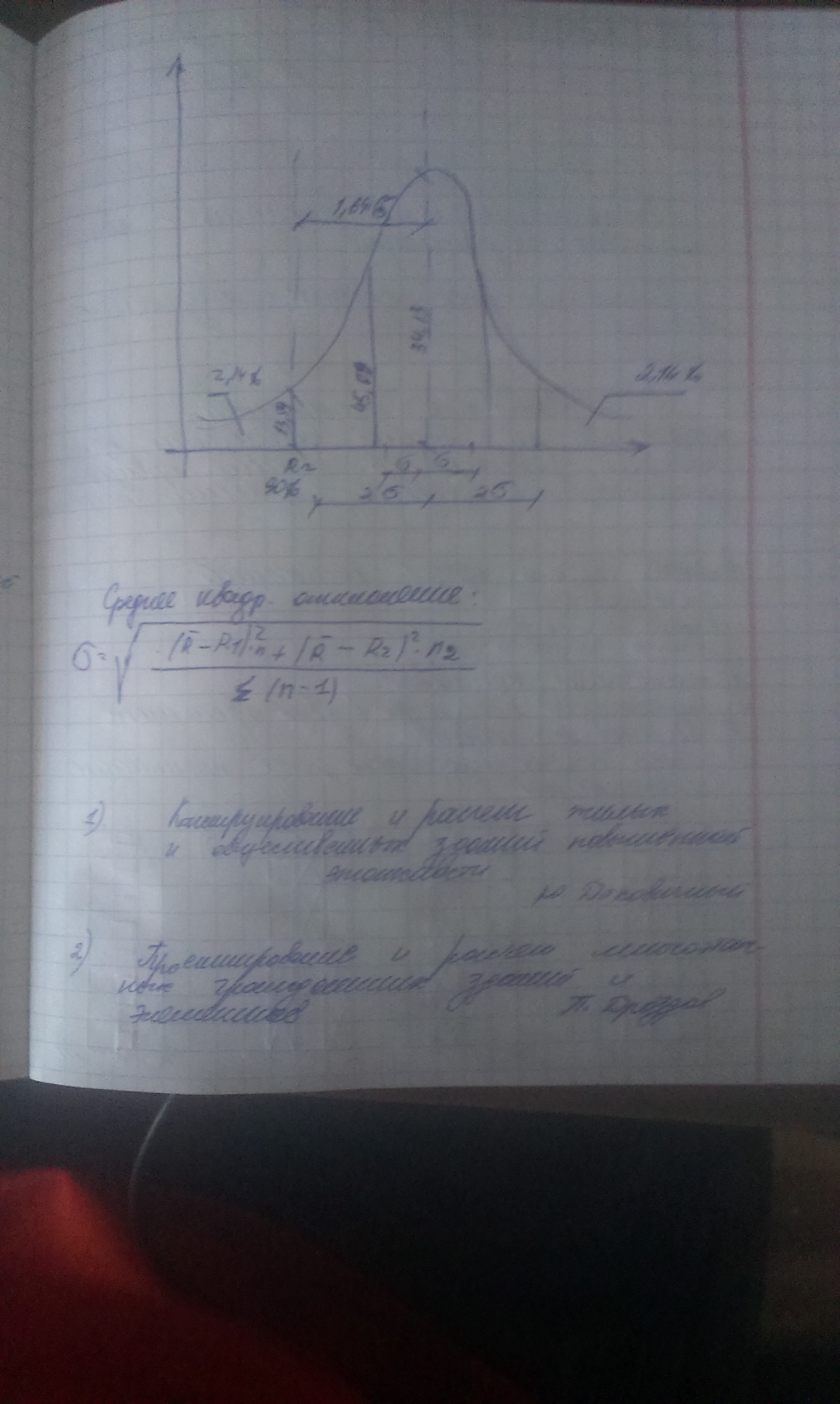 33. Закономерности случайных явлений для строительных конструкций. Событие - качественный или количественный результат опыта, осуществляемого при определенных условиях. Например, событие - попадание предела текучести стали  в интервал от 240 до 260 МПа. Событие может быть случайным, достоверным или невозможным. Объективная математическая оценка возможности реализации случайного события - вероятность. Вероятность есть объективная мера возможности наступления события независимо от того, является ли оно массовым или нет. В жизни все (полуинтуитивно) применяют вероятностные оценки будущим событиям и весьма успешно.Вероятностное поведение конструкций Роль случайных закономерностей в поведении конструкции Поведение конструкции на различных стадиях их функционирования носит случайный характер. Рассмотрим причины и природу этого явления. Одним из направлений современного развития теории расчета строительных конструкций является решение проблемы оценки надежности и взаимосвязанной с ней долговечностью зданий и сооружений. Кардинальный вопрос о способности конструкции сопротивляться внешним воздействиям в течение срока её службы с обеспечением требуемых эксплуатационных качеств может быть решен обоснованно и достоверно только на основе применения вероятностных подходов, лежащих в основе фундаментальных законов природы Строительным конструкциям, как показали исследования в нашей стране и за рубежом, свойственна случайная природа поведения на различных стадиях их функционирования. Опыт эксплуатации мостов, зданий и сооружении свидетельствует, что надежность и безотказная работа конструкций зависит от большого количества изменчивых факторов, определяющих как внешнее воздействие нагрузок при монтаже и эксплуатации, так и несущую способность конструкции по различным признакам выхода её из строя. 34. Математическое ожидание случайной величины прочности материала.
Математическое ожидание  - достоверная величина, т.к. вероятность того, что при n= испытаниях мы получим среднее арифметическое М(X)= равна 1.М(с)=с, М(сx) = сМ(x), где с – неслучайное число. Для независимых с.в. Х1 и Х2 М(x1+x2)=М(x1)+М(x2), М(x1x2)=М(x1)М(x2), М(x2)=[М(x)]2+D(x). К математическому ожиданию стремится среднее арифметическое наблюдаемых значений с.в. при количестве испытаний n. Геометрически м.о. – это абсцисса ц. т. площади под кривой плотности распределения. Размерность м.о. совпадает с размерностью с.в. 35. Биноминальное распределение случайных величин. Биноминальный закон распределения случайной величины Биноминальное распределение - это распределение вероятностей возможных чисел появления события А при n независимых испытаниях, в каждом из которых событие А может осуществиться с одной и той же вероятностью Р(А) = р = const. Кроме события А может произойти также противоположное событие Ā, вероятность которого Р(Ā) = 1 - р = q. Вероятности любого числа событий соответствуют членам разложения бинома Ньютона в степени, равной числу испытаний:  где pn - вероятность того, что при n испытаниях событие А наступит n раз; qn - вероятность того, что при n испытаниях событие А не наступит ни разу;  - вероятность того, что при n испытаниях событие А наступит m раз, а событие Ā наступит n-m раз; - число сочетаний (комбинаций) появления события А и Ā.Числовые характеристики биноминального распределения: М(m)=np - математическое ожидание частоты появления события А при n независимых испытаниях; D(m)=npq - дисперсия частоты появления события. А;  - среднее квадратическое отклонение частоты.36. Распределение случайных величин Пуассона. Распределе́ние Пуассо́на моделирует случайную величину, равную числу событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга. Определение Выберем фиксированное число  и определим дискретное распределение, задаваемое следующей функцией вероятности: ,где  обозначает факториал, — основание натурального логарифма.Тот факт, что случайная величина  имеет распределение Пуассона с параметром  , записывается:  .37. Показательным (экспоненциальным) называется распределение вероятностей непрерывной случайной величины X, которое описывается плотностью, имеющей вид 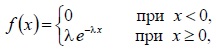 где λ – постоянная положительная величина Функция распределения  Вероятность попадания в интервал 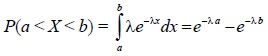 Математическое ожидание  Дисперсия  Среднее квадратическое отклонение 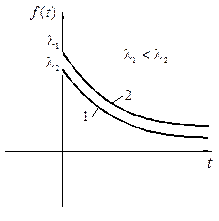   38. Нормальное распределение,также называемое распределением Гаусса — распределение вероятностей, которое в одномерном случае задается функцией плотности вероятности, совпадающей с функцией Гаусса:  где параметр μ — математическое ожидание (среднее значение), медиана и мода распределения, а параметр σ — среднеквадратическое отклонение (σ ² — дисперсия) распределения. Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений. Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием μ = 0 и стандартным отклонением σ = 1. Важное значение нормального распределения во многих областях науки (например, в математической статистике и статистической физике) вытекает из центральной предельной теоремы теории вероятностей. Если результат наблюдения является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то при увеличении числа слагаемых распределение центрированного и нормированного результата стремится к нормальному. Этот закон теории вероятностей имеет следствием широкое распространение нормального распределения, что и стало одной из причин его наименования. Плотность вероятности  |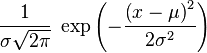
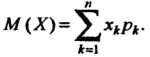С законом распределения (35.1) определяется формулой
(35.9)
Задана законом распределения (35.2), то
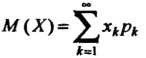(35.10)
, все значения которой принадлежат отрезку
, определяется формулой
(35.11)
, то
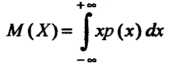(35.12)
