Система поддержки принятия решений по выбору тура. Система поддержки принятия решений по выбору тура

• Название: Система поддержки принятия решений по выбору тура
• Дата: 22.05.2021
• Размер: 1.81 Mb.
• Имя файла: Система поддержки принятия решений по выбору тура.docx
• Тип: Техническое задание; #208432
• страница: 7 из 11

3.1.2.3. Метод ELECTRE II

Отличается от метода ELECTRE I тем, что создаются по два индекса согласия и несогласия. Все альтернативы сравниваются относительно двух отношений. В результате образуется конечное множество альтернатив первого отношения, находящихся в сильном и в слабом предпочтениях. Выделяется часть менее предпочтительных альтернатив и они далее не рассматриваются. И так эта процедура повторяется еще раз и так далее. Таким образом альтернативам присваиваются ранги.

Таким же образом строится порядок второго отношения, только начиная с менее предпочтительных. Если получившиеся два списка не сильно различны, то составляется средний порядок слиянием этих списков. Этот порядок выдается ЛПР в качестве рекомендации решений задачи.

3.1.2.4. Метод ELECTRE III

В методе ELECTRE III используются порог чувствительности, который является псевдокритерием. Также как и в предыдущих методах ELECTRE I и ELECTRE II подсчитываются два индекса предпочтительности, но в отличии от них предпочтение той или иной альтернативы определяется с использованием порога чувствительности, который меняется до определенного предела. Каждой альтернативе при этом присваивается число равное разности индексов предпочтительности. Затем список альтернатив сортируется относительно полученных альтернативами чисел.

Во всех методах ELECTRE желательно, чтобы количество альтернатив было небольшим, а критерии были количественными.

3.1.2.5. Метод аналитических иерархий

В методе аналитических иерархий сначала происходит расчет веса каждого критерия, а затем согласно этим весам высчитывается цена альтернативы, чем больше цена, тем предпочтительнее альтернатива.

Для расчета весов критериев они попарно сравниваются, получая оценки отношения пар критериев из которых образуется обратно симметричная матрица.

Оценки имеют следующий смысл: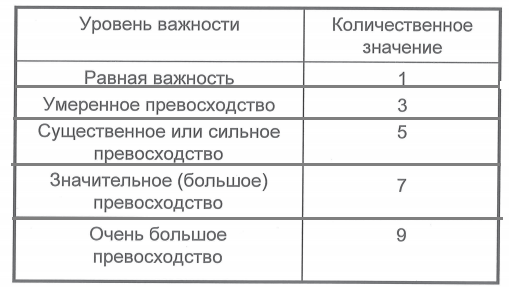



2, 4, 6, 8 - соответствующие промежуточные значения, которые используются реже.

После расчета цен альтернатив наступает время проверки согласованности суждений ЛПР. Проверка осуществляется с помощью индекса согласованности, который дает информацию о том насколько нарушена согласованность суждений. Если отклонения слишком велики и превышают некий установленный предел, то ЛПР придется перепроверить верность суждений, пересмотрев значения в матрице.

В этом методе количество альтернатив должно быть небольшим, а критерии любыми.

3.1.3. Методы, основанные на информации о допустимых значениях критериев

3.1.3.1. Задание минимально допустимых значений критериев

Метод использует количественные критерии, по значениям которых ЛПР определяет некоторую планку минимальных значений, в которые должна укладываться та или иная альтернатива. Происходит сравнение двух оценок по шкале одного критерия, множество альтернатив разделяется на удовлетворительные и неудовлетворительные. Количество альтернатив может быть любым.

3.1.3.2. Анализ альтернатив только по критериям, для которых достигаются «наилучшие»

Этот метод включает в себя задание минимально допустимых значений критериев, а также ЛПР выделяет альтернативы, удовлетворяющие его в наибольшей степени. Соответственно количество альтернатив – любое, критерии – количественные.

3.1.4. Методы, не требующие ранжирования критериев

3.1.4.1. Критерий Харвица

Критерий Харвица представляет из себя компромиссное решение между методами МАКСИМИН и МАКСИМАКС, то есть между пессимистичной и оптимистичной оценкой. Границей между этими оценками называется критерием Харвица, заключающемся в присвоении веса этим оценкам.

Умножив результаты на соответствующие веса и суммируя их, ЛПР получает общий результат. Далее выбирается альтернатива с наибольшим значением.

3.1.4.2. Метод МАКСИМИН

МАКСИМИН можно интерпретировать как наибольший выигрыш из тех, которые могут быть достигнуты ЛПР в наиболее проигрышных для него ситуациях, и, таким образом, будут представлять гарантированный выигрыш. Нахождение МАКСИМИНа как математической операции условно состоит в последовательном решении простых однокритериальных задач. Количество альтернатив может быть любым, а критерии количественными.