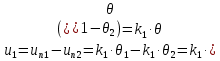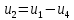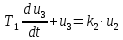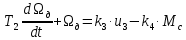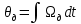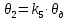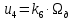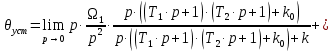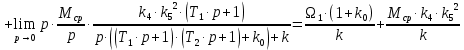Ргр. РГР Смирнова В. Р. (Исправленный). Система регулирования скорости вращения асинхронного электродвигателя
 Скачать 411.64 Kb. Скачать 411.64 Kb.
|
|
Нижегородский Государственный Технический Университет им. Р. Е. Алексеева Кафедра «Электрооборудование, электропривод и автоматика»Заведующий кафедрой: Дарьенков А. Б. (подпись) (фамилия, и., о.)  (дата)  РАСЧЁТНОГРАФИЧЕСКАЯ РАБОТА РАСЧЁТНОГРАФИЧЕСКАЯ РАБОТАпо дисциплине "Теория автоматического управления" тема: «Система регулирования скорости вращения асинхронного электродвигателя» вариант № 6.4 Руководитель: Мельников В. Л. (подпись) (фамилия, и., о.)  (дата) Студент: Смирнова В. Р. (подпись) (фамилия, и., о.)   18-ЭПА (дата) (группа или шифр)  Работа защищена Протокол № С оценкойНижний Новгород 2021 год СодержаниеРабота защищена 1 Протокол № 1 С оценкой 1 ЗАДАНИЕ ДЛЯ КУРСОВОЙ РАБОТЫ 3 2 ПОСТРОЕНИЕ СИСТЕМЫ 6 3.2 ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ЗВЕНЬЕВ СИСТЕМЫ 8 5 ПОДБОР СТАНДАРТНОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ. 14 17 17 8 РАСЧЁТ ПЕРЕХОДНОГО ПРОЦЕССА 18 Рассчитаем переходный процесс для регулируемой величины по задающему воздействию при мгновенном повороте входного вала на угол рад и при отсутствии момента сопротивления рабочей машины . 18 ЗАДАНИЕ ДЛЯ КУРСОВОЙ РАБОТЫ 2 1 ИСХОДНЫЕ ДАННЫЕ. 3 2 ПОСТРОЕНИЕ СИСТЕМЫ 5 2.1 ОПИСАНИЕ РАБОТЫ СИСТЕМЫ 5 2.2 ФУНКЦИОНАЛЬНАЯ СХЕМА 5 3 ОПЕРАТОРНЫЕ УРАВНЕНИЯ И ПЕРЕДАТОЧНЫЕ ФУНКЦИИ САР. СТУКТУРНАЯ СХЕМА САР 7 3.1 ОПРЕДЕЛЕНИЕ ОПЕРАТОРНЫХ УРАВНЕНИЙ 7 3.2 ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ЗВЕНЬЕВ СИСТЕМЫ 7 3.3 СТРУКТУРНАЯ СХЕМА САР 8 4 ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ ЗАМКНУТОЙ И РАЗОМКНУТОЙ СИСТЕМЫ 10 4.1 ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ РАЗОМКНУТОЙ СИСТЕМЫ 10 4.2 ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ЗАМКНУТОЙ СИСТЕМЫ 10 5 ПОДБОР СТАНДАРТНОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ УСИЛЕНИЯ И ВНУТРЕННЕЙ ОБРАТНОЙ СВЯЗИ 13 6 ПРОВЕРКА СИСТЕМЫ НА УСТОЙЧИВОСТЬ 15 7 ОПРЕДЕЛЕНИЕ УСТАНОВИВШЕЙСЯ ДИНАМИЧЕСКОЙ ОШИБКИ 16 8 РАСЧЁТ ПЕРЕХОДНОГО ПРОЦЕССА 17  ЗАДАНИЕ ДЛЯ КУРСОВОЙ РАБОТЫ1. Составить функциональную схему системы регулирования и объяснить её взаимосвязь с принципиальной схемой. Объяснить работу системы при изменении задающего и возмущающего воздействий. 2. Записать дифференциальные уравнения элементов в операторной форме при нулевых начальных условиях. Найти передаточные функции звеньев. Составить структурную схему системы. 3. Найти по структурной схеме передаточную функцию разомкнутой (по цепи главной обратной связи) системы  , передаточные функции замкнутой системы для регулируемой величины , передаточные функции замкнутой системы для регулируемой величины 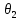 и для ошибки и для ошибки 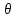 по задающему воздействию по задающему воздействию 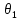 и по моменту сопротивления и по моменту сопротивления 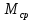 . Записать операторные уравнения для регулируемой величины и для ошибки. Получить характеристические уравнения разомкнутой и замкнутой систем и сравнить их между собой. . Записать операторные уравнения для регулируемой величины и для ошибки. Получить характеристические уравнения разомкнутой и замкнутой систем и сравнить их между собой.4. Подобрать стандартную передаточную функцию разомкнутой системы [8, с. 471], при которой порядок астатизма равен единице, а величина перерегулирования  и время регулирования и время регулирования 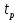 при отработке скачка задающего воздействия не превышают заданных значений. Определить коэффициент усиления при отработке скачка задающего воздействия не превышают заданных значений. Определить коэффициент усиления  и коэффициент внутренней обратной связи и коэффициент внутренней обратной связи 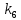 . .5. Проверить систему на устойчивость. 6. Вычислить установившуюся динамическую ошибку в режиме слежения с постоянной скоростью вращения входного вала 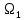 при наличии момента сопротивления при наличии момента сопротивления 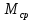 , создаваемого рабочей машиной. , создаваемого рабочей машиной.7. Рассчитать переходный процесс изменения регулируемой величины при мгновенном повороте входного вала на угол 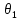 =1 рад и =1 рад и 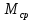 =0, оценить его качество и соответствие заданию. =0, оценить его качество и соответствие заданию.Примечание: при выполнении п. 7 внутреннюю обратную связь не объединять с главной обратной связью для того, чтобы размыкание главной обратной связи не  сопровождалось размыканием и дополнительной обратной связи. сопровождалось размыканием и дополнительной обратной связи.  1 ИСХОДНЫЕ ДАННЫЕ 1 ИСХОДНЫЕ ДАННЫЕ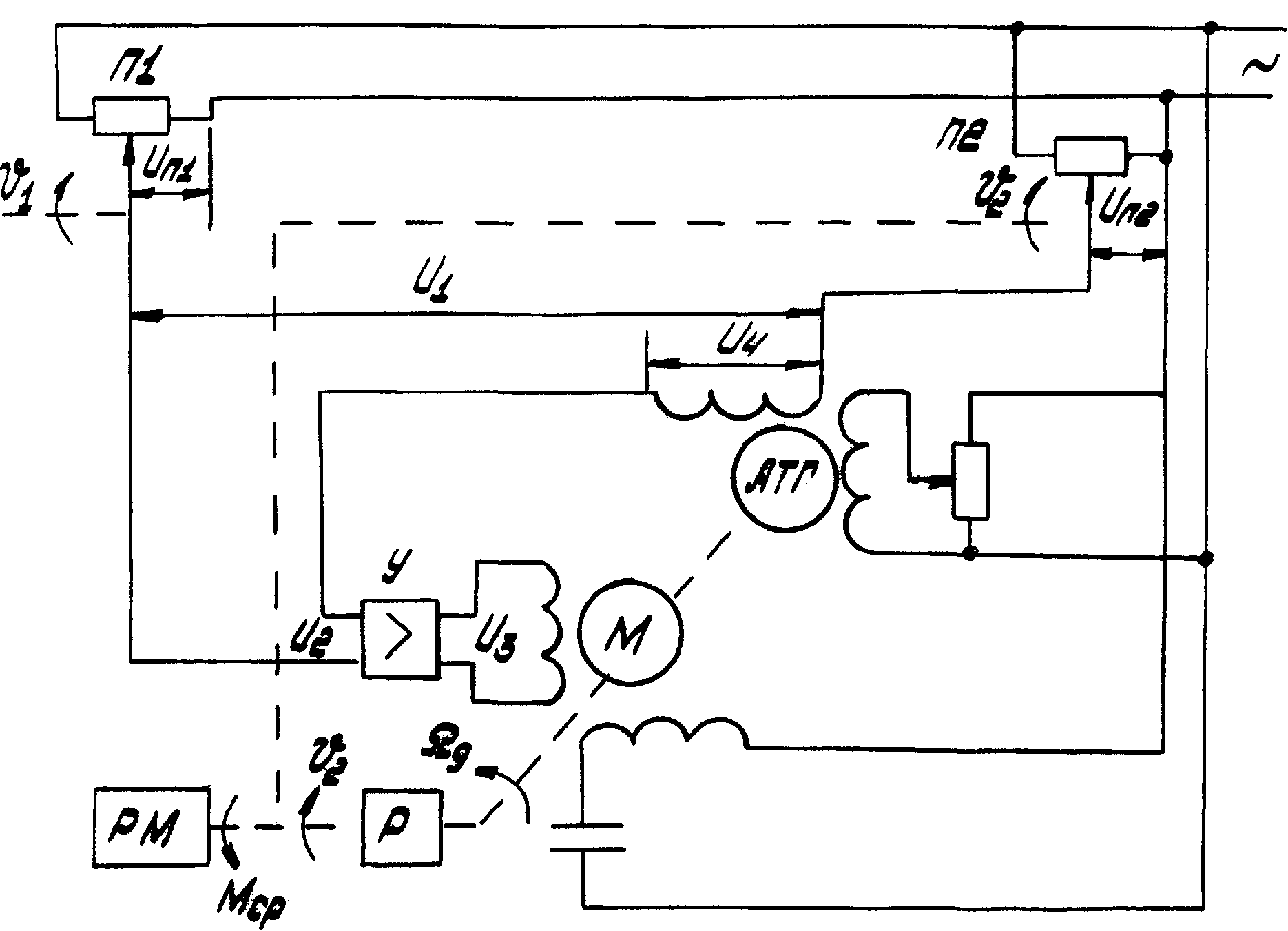 Рис. 1.1 – Принципиальная схема следящей системы где П1, П2 – потенциометрические датчики углов повората; У – усилитель; М – двухфазный асинхронный двигатель двигатель; АТГ – асинхронный тахогенератор; Р – редуктор; РМ – рабочая машина. Уравнения элементов системы: Элементы системы характеризуются следующими уравнениями динамики: Потенциометрический измеритель рассогласования:
Входная цепь усилителя:
Усилитель:
Электродвигатель:
Редуктор:
Тахогенератор:
где 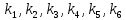 – передаточные коэффициенты; – передаточные коэффициенты; – постоянные времени усилителя и электродвигателя; – постоянные времени усилителя и электродвигателя;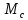 – момент сопротивления рабочей машины, приведенный к валу электродвигателя, – момент сопротивления рабочей машины, приведенный к валу электродвигателя,  ; ; 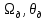 – угловая скорость и угол поворота вала электродвигателя. – угловая скорость и угол поворота вала электродвигателя.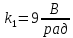 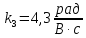  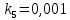  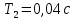 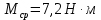 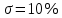 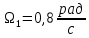 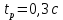 2 ПОСТРОЕНИЕ СИСТЕМЫСледящая система предназначена для дистанционного воспроизведения с заданной точностью любых законов движения, задаваемых командным органом. Система приведена на рисунке 1.1. 2.1 ОПИСАНИЕ РАБОТЫ СИСТЕМЫ Данная сиcтема регулирует выходную величину угла поворота машины 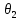 . При повороте задающего вала на угол . При повороте задающего вала на угол 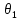 на выходе потенциометрического измерителя рассогласования возникнет напряжение рассогласования на выходе потенциометрического измерителя рассогласования возникнет напряжение рассогласования 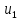 . Это напряжение будет подано на вход усилителя (У). Усиленное напряжение . Это напряжение будет подано на вход усилителя (У). Усиленное напряжение 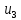 с выхода усилителя поступает на обмотку управления двухфазного асинхронного двигателя (М), который поворачивает через редуктор (Р) выходной вал в сторону уменьшения рассогласования до тех пор, пока угол с выхода усилителя поступает на обмотку управления двухфазного асинхронного двигателя (М), который поворачивает через редуктор (Р) выходной вал в сторону уменьшения рассогласования до тех пор, пока угол 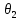 не станет примерно равным углу не станет примерно равным углу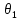 . В результате напряжение рассогласования . В результате напряжение рассогласования 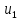 снижается до нуля, уменьшается также напряжения снижается до нуля, уменьшается также напряжения 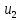 , , 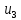 . После чего двигатель остановится. . После чего двигатель остановится.Для обеспечения устойчивости следящей системы и повышения ее качественных показателей усилитель и электродвигатель охвачены жесткой отрицательной обратной связью по скорости  , осуществляемой асинхронным тахогенератором (АТГ). , осуществляемой асинхронным тахогенератором (АТГ).При увеличении статического момента асинхронного двигателя, происходит изменение угловой скорости вращения вала электродвигателя, датчик скорости, механически связанный с двигателем, реагирует на данное изменение. Т.к. напряжение на выходе датчика пропорционально скорости вращения, то при его изменении, по средством ООС (отрицательной обратной связи) по напряжению происходит корректировка входного напряжения усилителя, что приводит к практически полному восстановлению скорости до прежней величины. То есть если момент сопротивления значительно возрос, а скорость вращения вала двигателя уменьшилась, то на входе усилителя будет существенно большее напряжение, и, соответственно, возрастет напряжение на обмотке двигателя, что увеличит развиваемый двигателем электрический момент и скорость вращения ротора до нужного уровня. 2.2 ФУНКЦИОНАЛЬНАЯ СХЕМА  Функциональную схему получаем путем синтеза элементов САР в соответствии с их назначением. Функциональную схему получаем путем синтеза элементов САР в соответствии с их назначением. Рисунок 2.1 – Функциональная схема САР  |
 | (3.1) |
3.2 ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ЗВЕНЬЕВ СИСТЕМЫ
Из системы уравнений (3.1), записанных в операторном виде, выведем передаточные функции для каждого звена САР:
Передаточная функция потенциометрического измерителя рассогласования:
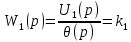 | (3.2) |
Первое звено – идеальное усилительное звено.
Передаточная функция усилителя:
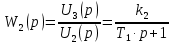 | (3.3) |
Второе звено – апериодическое звено первого порядка.
Передаточные функции электродвигателя:
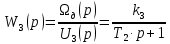 | (3.4) |
 | (3.5) |
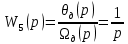 | (3.6) |

Третье и четвёртое звено – апериодическое звено первого порядка.
Пятое звено – интегрирующие звено.
Передаточные функции редуктора:
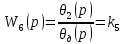 | (3.7) |
Шестое звено – идеальное усилительное звено.
Передаточные функции тахогенератора:
 | (3.8) |
Седьмое звено – идеальное усилительное звено.
3.3 СТРУКТУРНАЯ СХЕМА САР
Используя полученные передаточные функции звеньев САР, составим структурную схему САР.
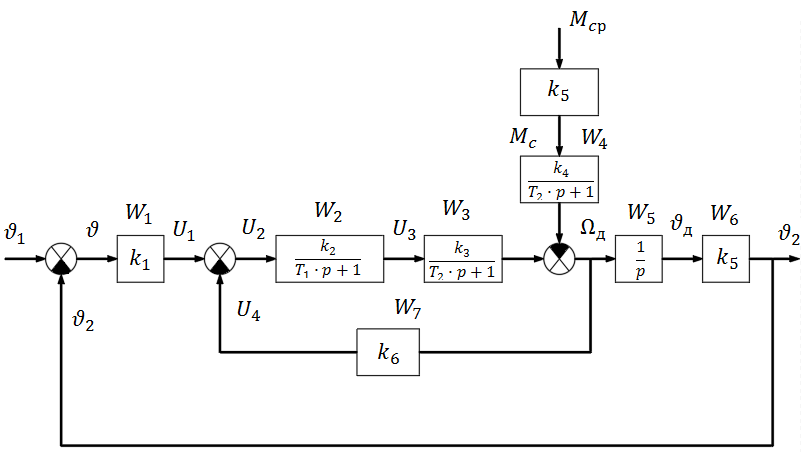
Рис 3.1 – Структурная схема САР

Преобразуем структурную схему САР (рисунок 3.1): заменяем встречно-параллельное соединение звеньев 2,3 и 7 одним звеном 8, и переносим сумматор влево через звенья 2,3.
Передаточная функция восьмого звена:
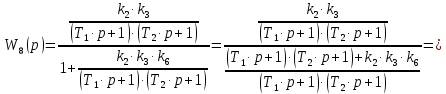 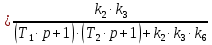 | (3.9) |
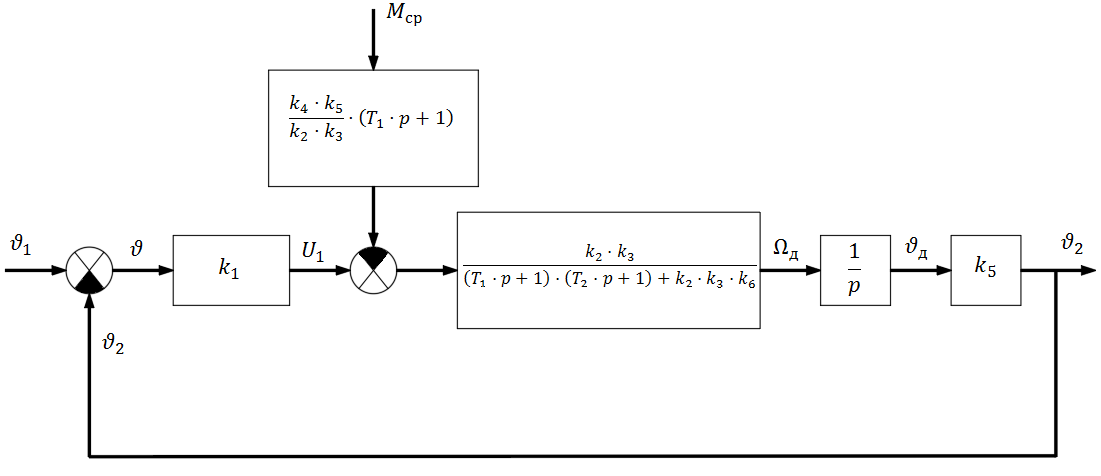
Рис 3.2 – Упрощенная структурная схема САР

4 ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ ЗАМКНУТОЙ И РАЗОМКНУТОЙ СИСТЕМЫ
4.1 ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ РАЗОМКНУТОЙ СИСТЕМЫ
Передаточную функцию разомкнутой системы (петли, разомкнутой по цепи главной обратной связи) определим по рис. 3.2:
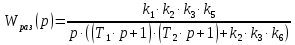 | (4.1) |
Введём обозначения для коэффициентов усиления:
 ;
; .
.Перепишем передаточную функцию разомкнутой системы с новыми обозначениями:
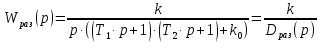 | (4.2) |
где
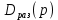 – характеристическое уравнение разомкнутой системы.
– характеристическое уравнение разомкнутой системы.4.2 ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ЗАМКНУТОЙ СИСТЕМЫ
Составим передаточную функцию замкнутой системы для регулируемой величину по задающему воздействию:
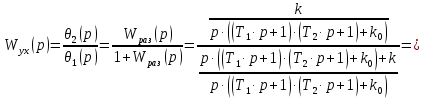
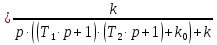
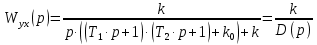 | (4.3) |
где
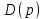 – характеристическое уравнение замкнутой системы.
– характеристическое уравнение замкнутой системы.Составим передаточную функцию замкнутой системы для регулируемой величину по возмущающему воздействию:

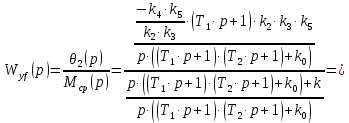

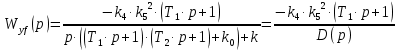 | (4.4) |
Составим передаточную функцию замкнутой системы для ошибки по задающему воздействию:
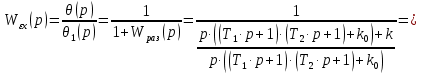
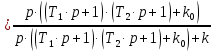
 | (4.5) |
Составим передаточную функцию замкнутой системы для ошибки по задающему воздействию:
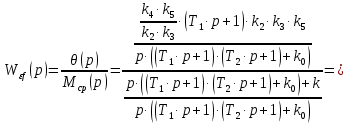
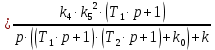

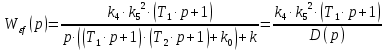 | (4.6) |
Сравним характеристические уравнения разомкнутой и замкнутой системы:
Характеристическое уравнение разомкнутой системы:
 | (4.7) |
Характеристическое уравнение замкнутой системы:
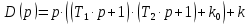 | (4.8) |
Из этих уравнений видно, что они различаются только коэффициентом усиления
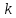 .
.Используя полученные выражения передаточных функций запишем операторные уравнения для выходной координаты и ошибки. Согласно принципу суперпозиции, выражение для выходной координаты:
 | (4.9) |
Подставим значения
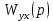 и
и 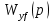 в уравнение (4.9):
в уравнение (4.9): 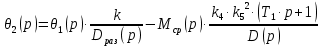 | (4.10) |
| | |
Согласно принципу суперпозиции, операторное изображение для ошибки:
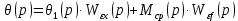 | (4.11) |
Подставим значения
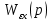 и
и 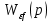 в уравнение (4.11):
в уравнение (4.11): 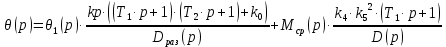 | (4.12) |

5 ПОДБОР СТАНДАРТНОЙ ПЕРЕДАТОЧНОЙ ФУНКЦИИ.
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ УСИЛЕНИЯ И ВНУТРЕННЕЙ ОБРАТНОЙ СВЯЗИ
Раскроем скобки в выражении для передаточной функции разомкнутой системы (4.2) и получим:
 | (5.1) |
По степени уравнения
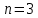 и порядку астатизма
и порядку астатизма  принимается следующая стандартная передаточная функция[1, c.25]:
принимается следующая стандартная передаточная функция[1, c.25]: 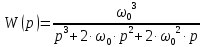 | (5.2) |
Преобразуем передаточную функцию разомкнутой системы (5.1) в соответствии с стандартной передаточной функцией (5.2) и получим:
 | (5.3) |
Приравняем соответствующие коэффициенты обеих передаточных функций:
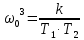 | (5.4) |
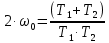 | (5.5) |
 | (5.6) |
Из уравнений (5.4) – (5.6) определим
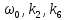 с учётом того, что
с учётом того, что 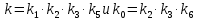 :
: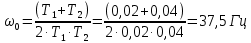


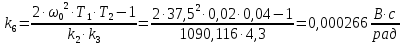
Найдём коэффициенты усиления
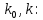
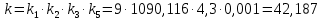

Передаточная функция разомкнутой системы имеет вид:
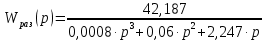 | (5.7) |

6 ПРОВЕРКА СИСТЕМЫ НА УСТОЙЧИВОСТЬ
Для проверки системы на устойчивость воспользуемся критерием Гурвица. Запишем характеристическое уравнение замкнутой системы:
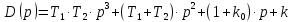 | (6.1) |
По критерию Гурвица, чтобы система была устойчива необходимо, чтобы все коэффициенты характеристического уравнения и диагональные миноры были больше нуля.
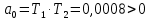
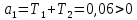
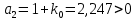
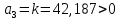
Составим определитель Гурвица:
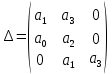 | (6.2) |
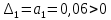
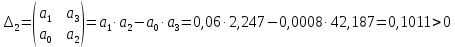
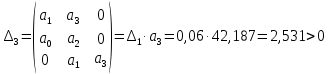
Все коэффициенты характеристического уравнения и диагональные миноры удовлетворяют критерию Гурвица. Следовательно, система устойчива.

7 ОПРЕДЕЛЕНИЕ УСТАНОВИВШЕЙСЯ ДИНАМИЧЕСКОЙ ОШИБКИ
Для вычисления установившейся динамической ошибки воспользуемся теоремой об установившемся значении оригинала:
 | (7.1) |
Определим установившеюся динамическую ошибку по её изображению (4.9) в режиме слежения с постоянной скоростью вращения входного вала
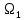 при наличии момента сопротивления
при наличии момента сопротивления 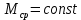 , создаваемого рабочей машиной:
, создаваемого рабочей машиной: 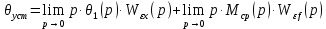 | (7.2) |
Определим изображения входного воздействия и момента сопротивления:
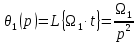 | (7.3) |
 | (7.4) |
Подставим выражения (7.3) и (7.4) в выражение (7.2):
Определим значение установившейся динамической ошибки:

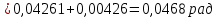


8 РАСЧЁТ ПЕРЕХОДНОГО ПРОЦЕССА
Рассчитаем переходный процесс для регулируемой величины по задающему воздействию при мгновенном повороте входного вала на угол рад и при отсутствии момента сопротивления рабочей машины
рад и при отсутствии момента сопротивления рабочей машины 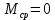 .
. Для расчета переходного процесса используем программный пакет SamSim:
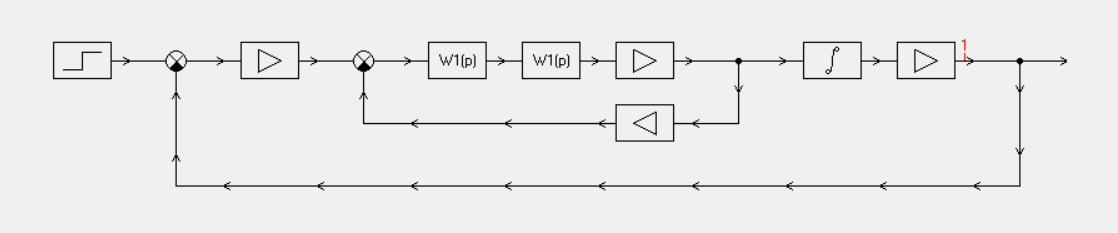
Рисунок 8.1 – Модель САР в SamSim.

Рисунок 8.1 – Переходный процесс САР.
По графику выходной координаты видно, что перерегулирование не превышает заданных 10%, и время регулирования выходной координаты так же находится в пределах заданных 0,3 секунд:
| | 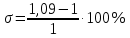 =9 =9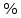 | (8.1) |
Система имеет приемлемые регулировочные качества и полностью соответствует заданию.

ЗАКЛЮЧЕНИЕ
В ходе проделанной работы была изучена следящая система автоматического регулирования двухфазного асинхронного электродвигателя.
При выполнении работы была построена функциональная схема САР по принципиальной схеме, были записаны дифференциальные уравнения и выведены передаточные функции каждого звена схемы. По передаточным функциям была построена структурная схема системы. По методу Гурвица была проверена система на устойчивость. По методическим указаниям были рассчитаны коэффициент усиления и коэффициент обратной связи, а также построен график переходного процесса САР.

 БИБЛИОГРАФИЧЕСКИЙ СПИСОК
БИБЛИОГРАФИЧЕСКИЙ СПИСОК1. Ваняев В.В., Мельников В.Л., Южбабенко В.Д. Методические указания к
курсовой работе по дисциплине "Теория автоматического управления" для
студентов по специальности 21.05. - Горький, ГПИ, 1988.
2. В.А. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования. М.: Наука, 1975.
3. СК СТО1 - У - 37.3 - 16 - 11 Стандарт организации. Общие требования к
оформлению пояснительных записок дипломных и курсовых проектов. /
НГТУ. – Нижний Новгород, 2011. – 26 с.