Практическая работа 1. Система счисления

• Название: Система счисления
• Дата: 10.01.2022
• Размер: 124.5 Kb.
• Имя файла: Практическая работа 1.doc
• Тип: Документы; #327744

Система счисления – это знаковая система, в которой числа записываются по определенным правилам, с помощью символов некоторого алфавита.

Символы алфавита, который используется для записи чисел, называются цифрами.

Системы счисления разделяются на две большие группы:

• 
  позиционные
  
• 
  непозиционные
  

1Непозиционные системы счисления

Самой распространенной из непозиционных систем счислении является римская. Мы пользуемся ею для обозначения юбилейных дат, для нумерации страниц книги (например, страниц предисловия), глав в книгах, строф в стихотворениях и т.д.

В этой системе в качестве цифр используются некоторые буквы. В настоящее время римские цифры выглядят так:

I = 1 V = 5 X = 10 L = 50 C = 100 D = 500 M = 1000

Значение цифры не зависит от ее положения в числе. Например, в числе XXX цифра X встречается трижды, и в каждом случае обозначает 10. Само число XXX означает 30.

Величина числа в римской системе счисления определяется как сумма или разность чисел.

Если меньшая цифра стоит слева от большей, то она вычитается, если справа – прибавляется.
Например, 1998 = 1000 + (1000 – 100) + (100 – 10) + 5 + 1 + 1 + 1 = M CM XC V I I I

Подряд одна и та же цифра ставится не более 3-х раз. Например, если число 80 = LXXX, то 90 записывается как XC, а не LXXXX.

2Позиционные системы счисления

Позиционные системы счисления используются для счета.

В позиционных системах счисления величина числа зависит от позиции цифры в числе. Например, в десятичной системе счисления числа 58 и 85 не равны, хотя содержат одни и те же цифры.

Любая позиционная система счисления характеризуется своим основанием.

основание позиционной системы счисления – это количество различных знаков или символов, которые используются для изображения цифр в данной системе счисления.

Основание системы счисления 10 2 8 16

Цифры, используемые в системе счисления 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 0, 1 0, 1, 2, 3, 4, 5, 6, 7 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, B, C, D, E, F

В принципе основанием системы счисления может быть любое натуральное число – два, три, четыре. Следовательно, возможно бесчисленное множество позиционных систем счисления: двоичная, троичная, четверичная и т.д.

Закономерность построения позиционных чисел имеет математическое представление.

Введем обозначения:

q – основание системы счисления;

a_i – любая цифра из множества цифр, принятых в данной системе счисления;

a_i удовлетворяет неравенству



и принимает в этом диапазоне только целые значения;

i – индекс, который обозначает номер разряда, занимаемого цифрой в числе.
Позицию для целых чисел обозначим номерами 1,2,…, n, а позиции в правильных дробях – номерами -1, -2,…, -m.

Тогда любое число А в произвольной позиционной системе счисления с основанием q можно записать следующим образом:

A_n = a_n-1q ^n-1 + a_n-2 q ^n-2 + … + a₁q ¹ + a₀q ⁰ + a _-1q ^-1 + … + a _{– m}q ^-m , (1)

гдеqⁱ называется позиционным значением или весом i – го разряда.

Для десятичной системы счисления понятие веса разряда соответствует названиям позиций – единицы, десятки, сотни, десятые доли, сотые доли и т.д.
ПРИМЕР:
Для десятичной системы счисления

Разряды 3 2 1 0

Число 2 1 2 4₁₀ = 2 х 10³ + 1 х 10² + 2 х 10¹ + 4 х 10⁰

Для двоичной системы счисления

Разряды 3 2 1 0 -1

Число 1 0 0 1, 1 ₂ = 1 х 2³ + 0 х 2² + 0 х 2¹ + 1 х 2 ⁰ + 1 х 2^-1

Для восьмеричной системы счисления

Разряды 3 2 1 0 -1 -2

Число 3 0 5 2, 4 1 ₈ = 3 х 8³ + 0 х 8² + 5 х 8¹ + 2 х 8 ⁰ + 4 х 8^-1 +1 х 8^-2

3Образование целых чисел в позиционных системах счисления. Правило счета.

В каждой системе счисления цифры упорядочены в соответствии с их значениями: 1 больше 0, 2 больше 1 и т.д.

Существует понятие продвижение цифры, которое означает замену ее следующей по величине.

Например, продвинуть цифру 1 значит заменить ее на 2, продвинуть цифру 2 значит заменить ее на 3 и т.д. Продвижение старшей цифры означает замену ее на 0.

Целые числа в любой системе счисления порождаются с помощью Правила счета:

Для образования целого числа, следующего за любым данным целым числом, нужно продвинуть самую правую цифру числа. Если какая-либо цифра после продвижения стала нулем, то нужно продвинуть цифру, стоящую слева от нее.
Применяя это правило, запишем первые пять целых чисел:

2{0,1} – в двоичной системе: 0, 1, 10, 11, 100,………..

3{0,1,2} – в троичной системе: 0, 1, 2, 10, 11,…………

5{0,1,2,3,4} – в пятеричной системе: 0, 1, 2, 3, 4,………….

8{0,1,2,3,4,5,6,7} – в восьмеричной системе: 0, 1, 2, 3, 4,………….

4Таблица соответствия между системами счисления

Кроме десятичной системы счисления используются системы счисления с основанием, являющимся целой степенью числа 2:

• 
  двоичная (используются цифры 0,1)
  
• 
  восьмеричная (используются цифры 0,1,…,7)
  
• 
  шестнадцатеричная (для первых целых чисел от нуля до девяти используются цифры 0,1,2,…,9, а для следующих чисел – от десяти до пятнадцати – в качестве цифр используются символы A, B, C, D, E, F).
  

Таблица соответствия между числами в этих системах счисления приведена ниже:

10 - я	2 - я	8 - я	16 -я		10 - я	2 - я	8 - я	16 -я
0	0	0	0		10	1010	12	A
1	1	1	1		11	1011	13	B
2	10	2	2		12	1100	14	C
3	11	3	3		13	1101	15	D
4	100	4	4		14	1110	16	E
5	101	5	5		15	1111	17	F
6	110	6	6		16	10000	20	10
7	111	7	7		17	10001	21	11
8	1000	10	8		18	10010	22	12
9	1001	11	9		19	10011	23	13

Двоичная система имеет некоторые преимущества перед другими системами счисления, например:

• 
  для ее реализации нужны технические устройства с двумя устойчивыми состояниями (есть ток – нет тока, намагничен – не намагничен и т.п.);
  
• 
  представление информации посредством только двух состояний надежно и помехоустойчиво;
  
• 
  возможно применение аппарата Булевой алгебры для выполнения логических преобразований информации;
  
• 
  двоичная арифметика намного проще десятичной.
  

Недостатком двоичной системы считается малая мощность ее алфавита (всего 2 числа – нуль и единица), вследствие чего представление числа «удлиняется» по сравнению с другими системами. Например, число 1024 в десятичной системе занимает 4 разряда, в двоичной - 11 разрядов (10000000000₂), в 16-ной – 3 (400₁₆).

5Правила перевода чисел из одной системы счисления в другую

5.1Перевод целого положительного числа из десятичной системы счисления в любую другую позиционную систему

Для перевода целого десятичного числа N в систему счисления с основанием q необходимо:

1. разделить исходное число N на основание системы q

2. выделить целую часть частного и остаток. Остаток будет являться младшим разрядом числа

3. целая часть принимается за исходное число и повторяется пункт 1 до тех пор, пока целая часть будет > q.

ПРИМЕР: Переведем число 53 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную.

в двоичную



в восьмеричную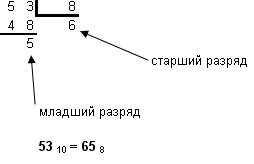



в шестнадцатеричную



Сделаем проверку. Используя формулу (1), переведем найденные числа в десятичную систему счисления.

110 101₂ = 1х2⁵ + 1х2⁴ + 0х2³ + 1х2² + 0х2¹ + 1х2⁰ = 32+ 16+ 0+ 4 + 0+ 1 = 53₁₀

65₈ = 6 х 8¹ + 5 х 8⁰ = 48 + 5 = 53₁₀

35₁₆ = 3 х 16¹ + 5 х 16⁰ = 48 + 5 = 53₁₀
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ. Перевести целое число из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную, аналогично примеру и сделать проверку.

Номер варианта	Число	Номер варианта	Число
1	123	9	276
2	165	10	142
3	205	11	213
4	247	12	178
5	134	13	235
6	226	14	153
7	181	15	253
8	268	16	194

5.2Перевод правильной десятичной дроби в любую другую позиционную систему счисления

Для перевода правильной десятичной дроби (дробь, в которой целая часть =0) F в систему счисления с основанием q необходимо:

1. умножить исходное число F на основание системы q

2. выделить целую и дробную части произведения. Целая часть является старшим после запятой разрядом искомого числа. Считать дробную часть произведения исходным числом и повторить пункт 1.

Умножение продолжается до тех пор, пока дробная часть произведения не станет равной 0 или не будет достигнута требуемая точность числа.
ПРИМЕР: Переведем число 0,375 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную.

в двоичную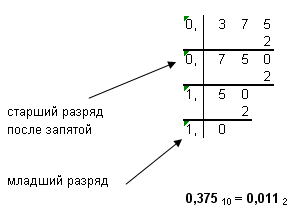



в восьмеричную



в шестнадцатеричную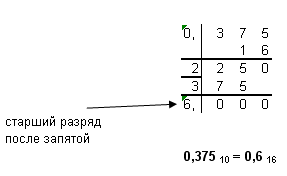


ПРИМЕР: Переведем число 0,6 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную.
в двоичную



в восьмеричную



в шестнадцатеричную:



ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ. Переведите десятичную дробь в двоичную, восьмеричную и шестнадцатеричную системы счисления.

Номер варианта	Число	Номер варианта	Число
1	0,12	9	0,51
2	0,36	10	0,17
3	0,42	11	0,83
4	0,54	12	0,28
5	0,67	13	0,49
6	0,23	14	0,62
7	0,76	15	0,31
8	0,94	16	0,92

Для чисел, имеющих целую и дробную части, перевод из десятичной системы счисления в другую осуществляется отдельно для целой и дробной части.
ПРИМЕР: 53,375₁₀ = 110 101,011₂ = 65,3₈ = 35,6₁₆