Сау_ла. Системы автоматического управления летательными аппаратами

• Название: Системы автоматического управления летательными аппаратами
• Дата: 05.03.2022
• Размер: 1.25 Mb.
• Имя файла: Сау_ла.doc
• Тип: Лабораторная работа; #383966
• страница: 1 из 3

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Уфимский государственный авиационный технический университет
Кафедра авиационного приборостроения

СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ЛЕТАТЕЛЬНЫМИ АППАРАТАМИ

Лабораторный практикум по дисциплине

«Системы автоматического управления

летательными аппаратами и их

силовыми установками»

Уфа 2006

Составитель В.И. Петунин
УДК 681.5: 629.73(07)

ББК 39.57(я7)

Системы автоматического управления летательными аппаратами: Лабораторный практикум по дисциплине «Системы автоматического управления летательными аппаратами и их силовыми установками» / Уфимск. гос. авиац. техн. ун-т; Сост. В.И. Петунин. – Уфа, 2006. – 45 с.

Лабораторный практикум содержит основные сведения о САУ углом тангажа самолета и о САУ скоростью полета с использованием автомата тяги. Главное внимание уделено изучению принципов построения САУ ЛА, методов их анализа и синтеза. Исследование динамических характеристик САУ производится с помощью пакета SimuLink системы Matlab.

Предназначен для студентов, обучающихся по направлению подготовки дипломированных специалистов 200100 «Приборостроение» и по специальности 200103 «Авиационные приборы и измерительно-вычислительные комплексы».

Табл. 3. Ил. 15. Библиогр.: 7 назв.

Рецензенты: д-р техн. наук, проф. Фрид А.И.,

канд. техн. наук, доц. Юлдашбаев Ш. А.

©Уфимский государственный

авиационный технический университет, 2006

Содержание
Введение 4
Лабораторная работа № 1. Исследование САУ углом тангажа

самолета 5
Лабораторная работа № 2. Исследование САУ скоростью полета

с использованием автомата тяги 14
Список литературы 27
Приложение 27

ВВЕДЕНИЕ
Расширение диапазонов изменения скоростей и высот полета привело к значительному изменению конструкции современных самолетов и связанному с этим ухудшению пилотажных характеристик. Поэтому появилась необходимость создания специальных автоматических систем, облегчающих пилотирование.

Системы автоматического управления (САУ) летательными аппаратами (ЛА) обеспечивают стабилизацию и управление угловыми движениями и движениями центра масс ЛА, а также управление некоторыми параметрами режима полета.

Вектор скорости центра масс ЛА как твердого тела в каждый момент времени направлен по касательной к траектории полета. Придание ЛА определенных угловых положений составляет основную задачу САУ угловыми движениями.

Обычно производится управление углами тангажа, крена, рыскания, атаки, скольжения и их производными.

Движение центра масс ЛА должно совершаться по определенной траектории. Выбор траектории полета обуславливается различными факторами, среди которых основными являются безопасность полета, экономичность, тактические соображения и др.

При реализации систем управления движением центра масс предусматривают управление высотой полета, боковым отклонением, пройденным расстоянием, горизонтальными, вертикальными и боковыми составляющими скоростей и ускорений.

Из рассмотрения задач, выполняемых САУ ЛА, видно, что они должны состоять из ряда автоматических устройств. Важнейшими такими устройствами являются автопилоты и автоматы тяги.

В лабораторном практикуме рассмотрены две наиболее распространенные системы:

лабораторная работа № 1 посвящена исследованию САУ углом тангажа самолета;

лабораторная работа № 2 посвящена исследованию САУ скоростью полета с использованием автомата тяги.

Исследование данных систем проводится с помощью пакета Simulink системы Matlab.

Лабораторная работа
Исследование САУ углом тангажа

САМОЛЕТА
1.1. Цель работы
Целью работы является изучение назначения, принципа действия и характеристик системы автоматического управления углом тангажа самолета; исследование методом математического моделирования влияния законов управления на основные характеристики системы.
1.2. Теоретическая часть

1.2.1. Автопилоты

Функциональная схема автопилота
Автопилотами называются автоматические устройства, воздействующие на управляющие органы самолета (рули высоты, рули направления, элероны) и обеспечивающие автоматическое пилотирование [1 - 4].

Автопилот является одним из важнейших элементов любой САУ ЛА. Автопилоты различаются структурными особенностями, законами управления, формой сигналов – носителей информации, числом каналов управления и др. Функциональная схема одного из каналов автопилота приведена на рис. 1.1. В состав автопилота входят датчики, предназначенные для получения информации о режимах и условиях полета; вычислители и корректирующие устройства, служащие для переработки информации и формирования законов управления; усилительные устройства и исполнительные механизмы (рулевые машины), служащие для усиления сигналов и перемещения органов управления самолета; устройства для формирования программы управления; устройства обратной связи; механизмы согласования; устройства для контроля работы системы и т.д.

Рис. 1.1. Функциональная схема автопилота
Структурные особенности автопилота оцениваются его законом управления, под которым подразумевают зависимость выходных сигналов исполнительных механизмов от совокупности входных сигналов.
Законы управления автопилотов
Под законом управления автопилота будем понимать требуемую зависимость между изменениями выходной и входных координат. При этом под выходной понимается координата, характеризующая положение исполнительного органа δ, под входными – координаты, сигналы которых вводятся в автопилот с помощью соответствующих датчиков x_i и задатчика x_з. Тогда для закона управления можно написать зависимость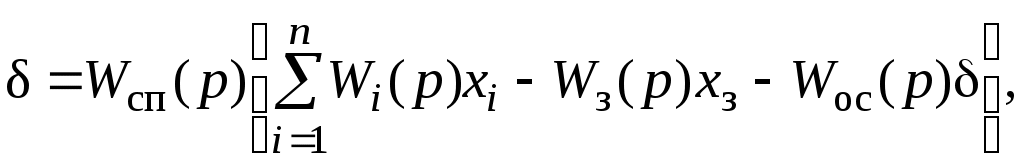

(1.1)

где – передаточные функции корректирующих устройств по регулируемым координатам; – передаточная функция корректирующего устройства по сигналу задатчика; – передаточная функция обратной связи; – передаточная функция сервопривода.

В зависимости от типа применяемой в сервоприводе автопилота обратной связи получаются автопилоты с разными законами управления.

1. Для автопилота с жесткой обратной связью (ЖОС)

. (1.2)

2. Для автопилота со скоростной обратной связью (СОС)

. (1.3)

3. Для автопилота с изодромной обратной связью (ИОС)

. (1.4)

Автопилоты по виду закона управления классифицируют на статические, в которых каждому положению исполнительного органа соответствует определенное значение регулируемого параметра, и астатические, в которых скорость исполнительного органа однозначно связана с регулируемым параметром. Рассмотренные законы управления (1.2)...(1.4) отличаются лишь видом левой части. Принципиальное отличие при этом имеет, однако, лишь наличие или отсутствие в левой части сомножителя p. По этому признаку закон управления в форме (1.2) называют статическим; законы управления в форме (1.3) и (1.4) – астатическими. Однако последняя классификация не совсем точна. Так, если по какой-либо входной координате x_i передаточная функция закона управления (1.1) будет соответствовать интегрирующему звену, то по отношению к этой координате автопилот будет астатическим, несмотря на наличие жесткой обратной связи. В тоже время автопилоты со скоростной или изодромной обратными связями, также как и автопилот без обратной связи, всегда являются астатическими. Роль интегрирующего звена в таких автопилотах играет рулевая машина сервопривода.

При постоянных возмущениях, действующих на объект управления, система со статическим автопилотом будет давать статические погрешности. Автопилоты со скоростной обратной связью не дают статических погрешностей, но оказываются более сложными. Вместе с тем, такие автопилоты обеспечивают более слабую реакцию самолета на турбулентные возмущения в атмосфере по сравнению со статическими автопилотами. Автопилоты с изодромной обратной связью отличаются от автопилотов со скоростной обратной связью тем, что в цепи обратной связи применяется не идеальное, а реальное дифференцирующее звено. Это обстоятельство позволяет обойтись в прямой цепи без сигналов, пропорциональных угловому ускорению, что упрощает схему автопилота.

Рассмотренные законы управления записаны в наиболее общей форме. В реальных автопилотах число входных координат редко превышает четыре (i = 1...4), передаточные функции и чаще всего представляют постоянные коэффициенты, реже имеют вид полинома или рациональной дроби первого порядка. Коэффициенты закона управления обычно называются передаточными числами автопилота.
Принцип действия канала тангажа САУ самолета
Углом тангажа называется угол, образуемый продольной осью ЛА с горизонтальной плоскостью. Изменение угла тангажа определяет продольное движение самолета. Система управления углом тангажа самолета служит для выдерживания нужной траектории движения в вертикальной плоскости. При этом предусматривается возможность изменения заданного угла тангажа вручную с места пилота или автоматически по сигналам, вырабатываемым системой траекторного управления.

Выходными координатами ЛА в продольном движении следует считать углы тангажа и наклона вектора скорости в вертикальной плоскости. Эти углы связаны с углом атаки .

При управлении углом тангажа происходит два движения: поворот продольной оси самолета вокруг поперечной оси и поворот вектора скорости центра масс в вертикальной плоскости. Поворот самолета вокруг поперечной оси осуществляется под действием продольных моментов, создаваемых рулем высоты, а поворот вектора скорости – под действием нормальных сил. При повороте продольной оси самолета на угол , изменяется угол атаки , что приводит к изменению момента статической устойчивости самолета (момент статической устойчивости – часть аэродинамического момента, пропорциональная углу атаки) и к изменению подъемной силы, что является причиной поворота вектора скорости.

Рассмотрим автоматическое управление углом тангажа, которое можно осуществить по схеме, представленной на рис. 1.2. В качестве чувствительных элементов в этом канале используются гировертикаль и скоростной гироскоп. Сигналы датчиков, обратной связи и задатчика после суммирования в вычислителе поступают на усилитель и затем на рулевую машину, которая перемещает руль высоты.

Предположим, что обратная связь в автопилоте является жесткой, а сигнал скоростного гироскопа отсутствует, тогда закон управления можно представить в виде

. (1.5)

При появлении рассогласования 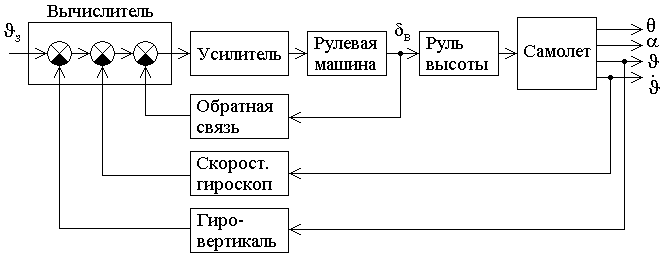происходит отклонение руля высоты на величину δ_в и создается продольный момент M_z, пропорциональный рассогласованию , под действием которого продольная ось самолета будет поворачиваться в сторону уменьшения величины . При повороте продольной оси самолета вектор скорости вначале не меняет своего направления, поэтому получает приращение угол атаки . Возникающий при этом момент собственной устойчивости, совпадающий по знаку с моментом руля, стремится возвратить продольную ось самолета к положению . При движении самолета под действием моментов руля и собственной устойчивости возникает демпфирующий момент, пропорциональный угловой скорости и направленный против движущих моментов.

Рис. 1.2. Функциональная схема канала тангажа
Поскольку демпфирующий момент мал, то под действием движущих моментов ось самолета перейдет через положение равновесия и процесс регулирования будет колебательным.

Для улучшения процесса управления необходимо увеличить демпфирующий момент путем введения в закон управления сигнала, пропорционального угловой скорости тангажа :

. (1.6)

Особенностью автопилота с жесткой обратной связью является наличие статической ошибки по углу тангажа при действии возмущения. Для устранения статической ошибки применяют астатические автопилоты со скоростной или изодромной обратной связью. Если обратная связь является скоростной, то закон управления автопилота принимает вид

, (1.7)

где – сигнал углового ускорения, который служит для создания демпфирующего момента.
1.2.2. Управление углом тангажа
Требования к качеству переходных процессов
При расчете параметров канала тангажа автопилота в качестве заданных значений переходного процесса обычно принимают следующие значения [4]: ; ; .
Математическое описание самолета по углу тангажа
В случае короткопериодического движения самолета по углам атаки и тангажа при горизонтальном полете уравнения движения будут иметь вид [3]:

(1.8)

где , , , , – безразмерные коэффициенты, зависящие от конструкции самолета, , – внешние возмущения, – отклонение руля высоты.

Из уравнений (1.8) путем преобразования Лапласа при нулевых начальных условиях можно получить передаточную функцию самолета по углу тангажа при управлении рулем высоты :

, (1.9)

где ; .
Простейшие законы управления углом тангажа
Рассмотрим статическую систему автоматического управления углом тангажа (рис. 1.3), включающую контур управления угловой скоростью и контур управления углом тангажа. Передаточная функция ЛА взята в предположении постоянства скорости полета. На структурной схеме не показаны внешние возмущения и , действующие на ЛА. Закон управления системы берем в виде

, (1.10)

где – заданное значение угла тангажа; , – передаточные числа.

Рис. 1.3. Структурная схема статической системы управления углом тангажа
Решая уравнение (1.5.1) совместно с уравнениями (1.1) получим

,

(1.11)

где ; ; ; .

Рассматриваемая система обладает статической ошибкой. Чтобы определить эту ошибку в уравнении (1.11), примем . Тогда при условии найдем

(1.12)

Отсюда следует, что чем больше передаточное число , тем меньше статическая ошибка. Однако при значительном система может стать неустойчивой вследствие динамических погрешностей в элементах автопилота, которые не учтены в уравнении (1.10).

Выбор параметров системы управления следует производить из условий неискаженного воспроизведения заданного угла тангажа при слабом реагировании на возмущения и .

Для внешнего замкнутого контура (см. рис. 1.3) можно написать:

, (1.13)

где: и – стандартные коэффициенты; – собственная частота;

; ; .

Известно, что параметры Вышнеградского и соответствуют оптимальному переходному процессу, если они меняются от двух до трех.

Тогда получаем следующую систему трех уравнений относительно трех неизвестных , и :



Собственная частота определяется из решения кубического уравнения

, (1.14)

тогда передаточные числа автопилота

(1.15)

Следовательно, если известны параметры ЛА, то по формулам (1.14) и (1.15) можно найти значения передаточных чисел , и собственную частоту .

Рассмотрим некоторые вопросы динамики автоматического управления углом тангажа посредством астатического автопилота со скоростной обратной связью (рис. 1.4). Закон управления примем в виде

, (1.16)

где – передаточные числа.

Рис. 1.4. Структурная схема астатической системы управления углом тангажа
Для исследования переходных процессов решим уравнение (1.16) совместно с уравнениями (1.8).

В результате получим уравнение замкнутой системы

, (1.17)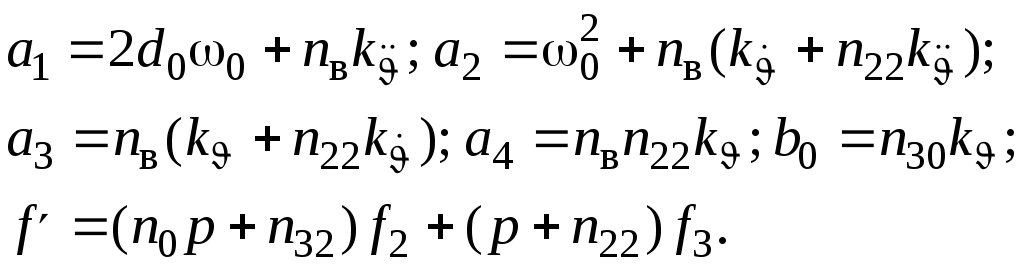

где



Поскольку возмущение входит под знак оператора дифференцирования, то система не имеет статических погрешностей по отношению к углу тангажа.

Рассмотрим передаточную функцию САУ по управляющему сигналу

, (1.18)

где и – стандартные коэффициенты; – собственная частота; .

Выберем параметры систем из условия кратности корней и .

Тогда получаем следующую систему четырех уравнений относительно четырех неизвестных , и :



Передаточные числа при этих условиях будут:

, (1.19)

где

. (1.20)

Рассмотренные упрощенные законы управления и методики синтеза передаточных чисел автопилота угла тангажа, приведенные в учебниках [1 - 3] не учитывают числитель передаточной функции самолета и поэтому не позволяют получить заданное качество переходных процессов в САУ углом тангажа. Собственная частота системы , определяемая при синтезе, не позволяет задать необходимое время переходного процесса. Необходимое качество переходных процессов может быть получено путем усложнения законов управления и приближения передаточной функции замкнутой системы к желаемой передаточной функции с помощью метода стандартных переходных характеристик.
1.2.3. Синтез законов управления автопилота
Расчет систем управления методом стандартных переходных характеристик
Аналитический синтез передаточных чисел автопилота с учетом заданного качества САУ удобно производить с помощью метода стандартных переходных характеристик [1, 6]. Суть этого метода расчета заключается в следующем. Выводится передаточная функция замкнутой системы 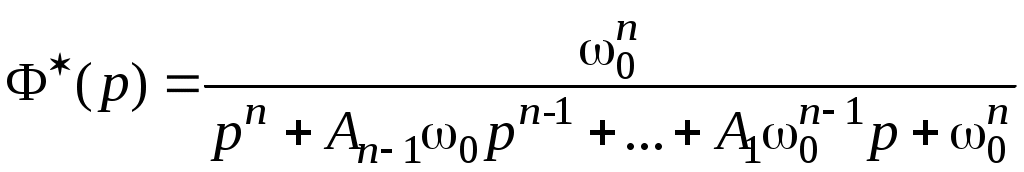для выбранной структуры закона управления. Если передаточная функция не содержит нули, то ее следует приблизить к стандартной передаточной функции вида

, (1.21)

где A_i – заданные коэффициенты; n – порядок системы.

Значение среднегеометрического корня выбирается из условия получения необходимого быстродействия, т.е. времени регулирования. Для случая кратных корней коэффициенты А_i равны биноминальным и переходный процесс является монотонным. Однако более быстрый переходный процесс соответствует значениям, приведенным в [6]. Корни характеристического уравнения системы (1.21) для этих значений коэффициентов являются комплексными, и переходный процесс имеет небольшое перерегулирование.

Если передаточная функция системы имеет нули, то оптимальный переходный процесс будет обеспечен при ином расположении полюсов, чем в случае, когда нули отсутствуют. Для определения этих полюсов найдем условия равенства двух передаточных функций 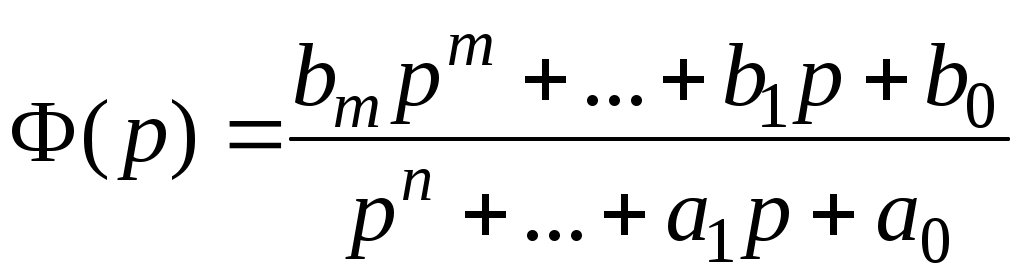и , имеющих вид:

; (1.22)

, (1.23)

где – передаточная функция рассматриваемой автоматической системы; – передаточная функция с известным качеством переходного процесса; .

При равенстве передаточных функций (1.22) и (1.23)

(1.24)

получаем



(1.25)

Равенство (1.25) может быть достигнуто за счет соответствующего подбора величин b_i и a_i передаточной функции (1.22) путем изменения передаточных чисел закона управления. При этом рассчитываемая система будет иметь заданные динамические свойства.
САУ углом тангажа посредством статического автопилота
Рассмотрим статическую систему автоматического управления углом тангажа, включающую контур управления угловой скоростью и контур управления углом тангажа.

Закон управления в случае статического автопилота примем в виде [5]:

(1.26)

где – заданное значение угла тангажа; , – коэффициенты закона управления (передаточные числа).

Решая систему уравнений (1.8) совместно с законом управления (1.26), получим уравнение замкнутой системы

,

(1.27)

Данная САУ, как и в случае пункта 1.2.2, обладает статической ошибкой при действии возмущений. Выбор параметров закона управления в общем случае производится на основе минимизации некоторого функционала качества замкнутой системы. Выбранные таким образом параметры должны обеспечивать воспроизведение с допустимой погрешностью заданного угла тангажа при слабом реагировании на возмущения f₂ и f₃.

Структурная схема САУ углом тангажа посредством статического автопилота с жесткой обратной связью изображена на рис. 1.5.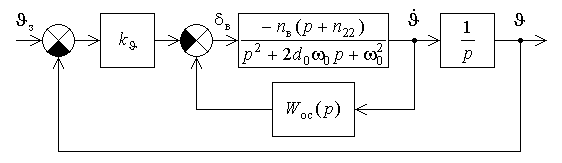

Рис. 1.5. Структурная схема САУ углом тангажа посредством статического автопилота с ЖОС

Передаточная функция ЛА по угловой скорости тангажа:

. (1.28)

Передаточная функция ОС:

. (1.29)

Передаточная функция внутренней подсистемы по угловой скорости тангажа имеет вид:



Передаточная функция замкнутой системы по углу тангажа имеет вид:

. (1.30)

Так как разность полиномов знаменателя и числителя передаточной функции рассматриваемой системы равна двум, то задаем желаемые передаточные функции системы в виде:

; (1.31)

, (1.32)

где – передаточная функция разомкнутой системы;

; .

Задавая значения и , которые характеризуют желаемое качество переходного процесса, определяем значения k и τ желаемой передаточной функции разомкнутой системы:

; . (1.33)

Приравняем передаточную функцию разомкнутой системы к желаемой передаточной функции :

(1.34)

или

.

После преобразований получаем





Приравнивая коэффициенты при соответствующих степенях оператора , получаем систему трех уравнений с тремя неизвестными :

(1.35)

Отсюда находим передаточные числа автопилота: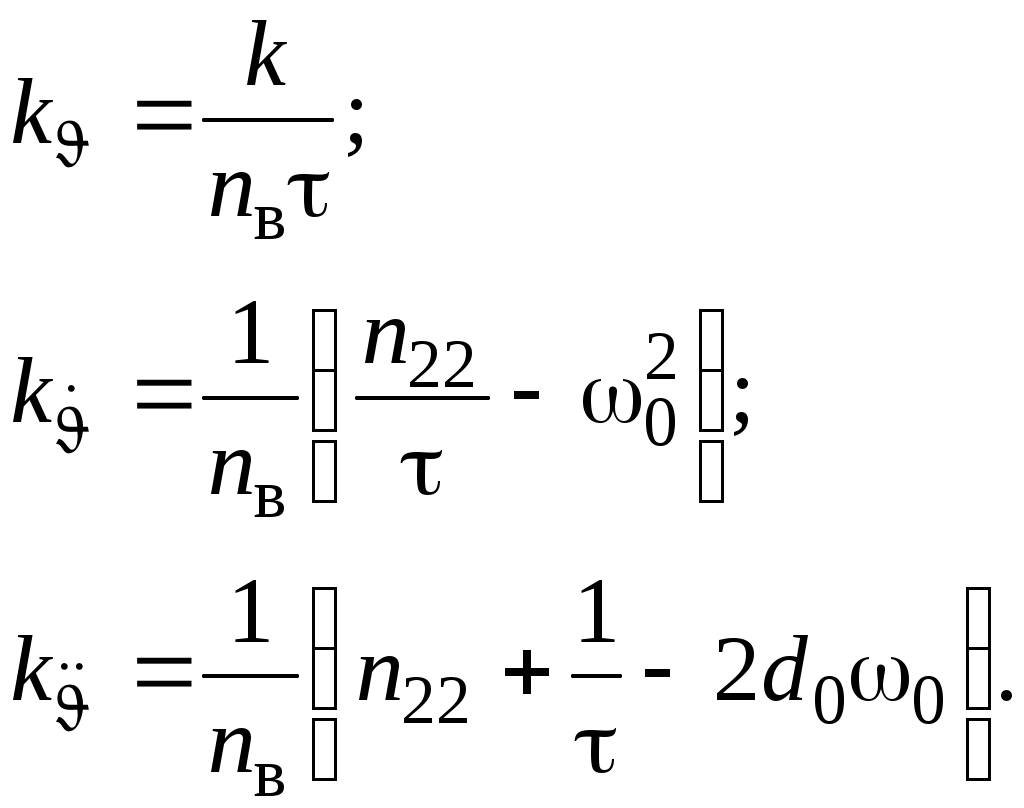

(1.36)

Определим параметры для легкого самолета с коэффициентами: ; ; ; ; ;

при ; ; ; :

;

при ; ; ; :

.

САУ углом тангажа посредством астатического автопилота
Динамика самолета описывается как и в предыдущем пункте уравнениями (1.8). Закон управления в случае астатического автопилота имеет вид [5]:

, (1.37)

где коэффициенты – передаточные числа.

Решив систему уравнений (1.8) совместно с (1.37), получим уравнение замкнутой системы:

, (1.38)

где .

Аналогично пункту 1.2.2 можно сделать вывод, что поскольку возмущение входит под знак оператора дифференцирования, то система не имеет статических погрешностей (является астатической) по отношению к углу тангажа при действии возмущений.

Структурная схема САУ углом тангажа посредством астатического автопилота со скоростной обратной связью изображена на рис. 1.6.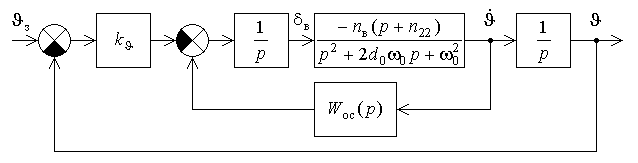


Рис. 1.6. Структурная схема САУ углом тангажа посредством астатического автопилота с СОС
Здесь передаточная функция ЛА по угловой скорости тангажа аналогична (1.28).

Передаточная функция ОС:

. (1.39)

Передаточная функция внутренней подсистемы по угловой скорости тангажа имеет вид:



.

Передаточная функция замкнутой системы по углу тангажа имеет вид:

. (1.40)

Так как разность полиномов знаменателя и числителя передаточной функции рассматриваемой системы равна трем, то задаем желаемые передаточные функции системы в виде:

; (1.41)

, (1.42)

где – передаточная функция разомкнутой системы;

; ; .

Задавая значения А₁, А₂ и , которые характеризуют желаемое качество переходного процесса, определяем значения k, τ₁ и τ₂ желаемой передаточной функции разомкнутой системы:

; ; . (1.43)

Приравняем передаточную функцию разомкнутой системы к желаемой передаточной функции :

(1.44)

или

.

После преобразований получаем



.

Приравнивая коэффициенты при соответствующих степенях оператора , получаем систему четырех уравнений с четырьмя неизвестными :

(1.45)

Отсюда находим передаточные числа автопилота:

(1.46)

Определим параметры для легкого самолета с коэффициентами: ; ; ; ; ;

при ; ; ; :

;

при ; ; ; :

.

Полученные передаточные числа являются безразмерными величинами.