Сау_ла. Системы автоматического управления летательными аппаратами
 Скачать 1.25 Mb.
|
|
1.3. Задание 1. Изучить принципы построения САУ углом тангажа самолета. 2. Рассчитать основные параметры законов управления для статического и астатического автопилота на ЭВМ. 3. Экспериментально исследовать САУ с различными законами управления на ЭВМ. 1.4. Описание лабораторной установки Лабораторной установкой является ЦВМ IBM PC для проведения цифрового моделирования. При исследовании динамических характеристик САУ углом тангажа самолета сначала проводится исследование статической системы (рис. 1.5), а затем астатической системы (рис. 1.6) при наличии и отсутствии обратной связи по угловой скорости. Переходные процессы в САУ определяются сначала при единичном ступенчатом сигнале по задающему воздействию, а затем по возмущению. Значения основных параметров самолета приведены в таблице. Так как коэффициенты самолета являются безразмерными, то и передаточные числа автопилота при синтезе получаются также безразмерными. Если эти параметры использовать при моделировании, то переходные процессы получаем в относительном времени  , где  – аэродинамическая постоянная времени самолета. Тогда реальное время  .
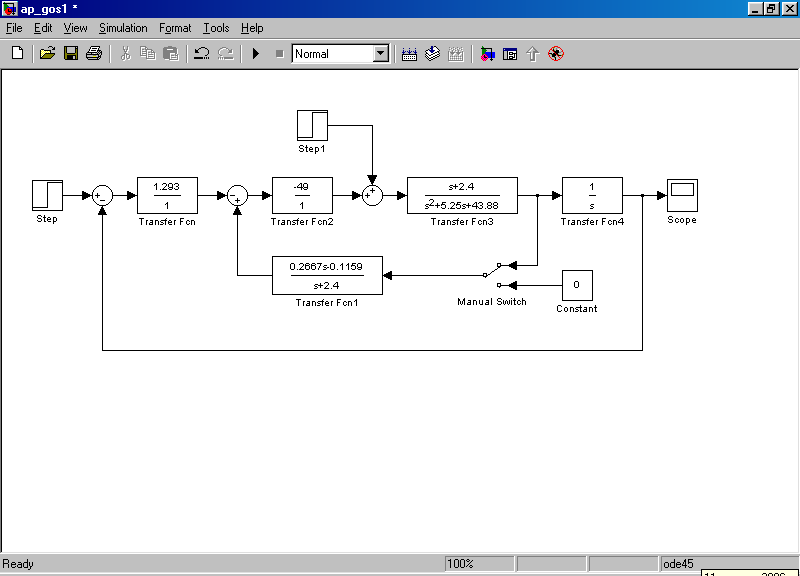 Рис. 1.7. Схема моделирования статической САУ углом тангажа 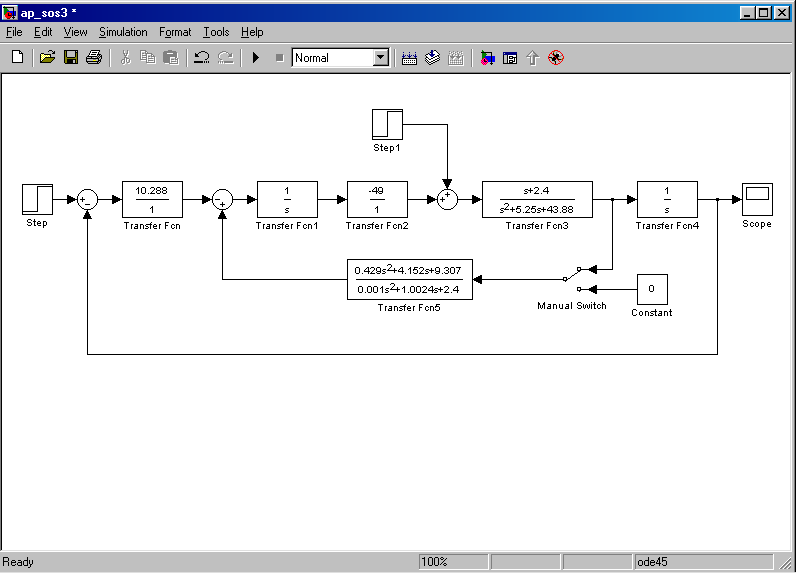 Рис. 1.8. Схема моделирования астатической САУ углом тангажа Цифровое моделирование переходных процессов, происходящих в САУ при подаче на вход единичного воздействия производится с использованием пакета SimuLink системы Matlab. Схемы моделирования приведены соответственно на рис. 1.7 и рис. 1.8. Параметры самолета задаются с помощью блоков Transfer Fcn2 и Transfer Fcn3, параметры автопилота – с помощью блоков Transfer Fcn и Transfer Fcn1 или Transfer Fcn и Transfer Fcn5. Входным сигналом САУ является единичное, ступенчатое изме-нение  (блок Step) или  (блок Step1). На выходе схемы с помощью блока Scope наблюдается переходной процесс по выходной координате системы  .Включение обратной связи по угловой скорости тангажа осуществляется при верхнем положении переключателя Manual Switch, при нижнем положении этого переключателя обратная связь отключается. 1.5. Порядок выполнения работы Задание 1. Аналитическое исследование динамических характеристик САУ углом тангажа самолета 1.1. Ознакомиться со структурными схемами статического и астатического управления углом тангажа. 1.2. Для заданного преподавателем режима полета самолета, рассчитать передаточные числа статической (1.36) и астатической (1.46) САУ углом тангажа. При этом для статической САУ  ; для астатической –  .При нахождении передаточных чисел необходимо использовать безразмерную частоту  , которая связана с размерной частотой  следующей зависимостью: ,где  .1.3. Оценить устойчивость и качество переходных процессов рассмотренных САУ с помощью формул преобразования Лапласа. Задание 2. Экспериментальное исследование САУ углом тангажа самолета на ЭВМ 2.1. Ввести соответствующую модель в память ЭВМ. Выставить заданные значения параметров на схеме моделирования. 2.2. Определить переходные процессы по задающему воздействию и по возмущению в статической САУ углом тангажа по выходной координате при разомкнутой и замкнутой обратной связи по угловой скорости. Обратить внимание на статическую точность САУ и качество переходных процессов. 2.3. Определить переходные процессы по задающему воздействию и по возмущению в астатической САУ углом тангажа по выходной координате при разомкнутой и замкнутой обратной связи по угловой скорости. Обратить внимание на статическую точность САУ и качество переходных процессов. 1.6. Требования к отчету Отчет по работе должен содержать: 1. Цель работы; 2. Структурные схемы; 3. Результаты расчетов; 4. Результаты моделирования; 5. Выводы. По заданию 1 отчет должен содержать структурные схемы САУ углом тангажа, передаточные функции и значения рассчитанных параметров систем. По заданию 2 отчет должен содержать графики переходных процессов и выводы по соответствию экспериментальных данных расчетным значениям. 1.7. Контрольные вопросы 1. Назначение системы управления угловым движением самолета. 2. Как определяется угол тангажа? 3. Принцип работы САУ углом тангажа. 4. Основные требования к САУ углом тангажа. 5. В чем отличие статического и астатического законов управления? 6. Какие недостатки характерны простейшим законам управления углом тангажа? 7. В чем заключается метод синтеза с помощью стандартных переходных характеристик? 8. Влияние обратной связи по угловой скорости тангажа на качество переходных процессов в САУ. Лабораторная работа № 2 Исследование САУ скоростью полета с использованием автомата тяги 2.1. Цель работыАналитическое и экспериментальное исследование САУ скоростью полета с использованием автомата тяги. 2.2. Теоретическая часть Движение центра масс ЛА должно совершаться по определенной траектории. Выбор траектории полета обусловливается различными факторами, среди которых основными являются безопасность полета, экономичность, тактические соображения и др. При реализации систем управления движением центра масс предусматривают управление высотой полета, боковым отклонением, пройденным расстоянием, горизонтальными, вертикальными и боковыми составляющими скоростей и ускорений [1 - 3]. Скорость самолета в горизонтальном полете определяется из уравнения  . (2.1)Сила тяги  и сопротивление  зависят от скорости полета. В установившемся режиме полета сила тяги равна силе сопротивления , т.е.  . Из этого равенства можно определить величину установившейся скорости полета. В неустановившемся движении величина ускорения  и характер её изменения определяются видом функции  и  .Самолет по отношению к скорости полета может быть устойчивым или неустойчивым в зависимости от взаимного протекания характеристик в точке их пересечения. Полагая, что скорость  соответствует равенству и беря линейные члены разложения функций и в ряды по малым приращениям  , преобразуем уравнение (2.1) к виду . (2.2)Если положить приближенно  , то условие устойчивости самолета по отношению к скорости полета примет вид при  . (2.3)При нарушении этого неравенства самолет становится неустойчивым по отношению к скорости полета. Для самолетов с поршневым двигателем и дозвуковых самолетов с турбореактивными двигателями условие (2.3) выполняется. Однако для сверхзвуковых самолетов, особенно на предельной высоте, может быть несколько точек пересечения и , среди которых есть и неустойчивые. Из изложенного следует, что в целях облегчения пилотирования сверхзвуковых самолетов целесообразно применять автоматические системы управления скоростью полета. Необходимость управления скоростью полета возникает также при режимах захода на посадку, при наведении самолета на цели, при полете в строю и др.Для управления скоростью полета можно воздействовать на тягу двигателя и на руль высоты. Изменение тяги двигателя достигается его дросселированием, что при наличии объединенного управления сводится к перемещению ручки управления двигателем. При воздействии на руль высоты меняется угол атаки, что ведет к изменению силы сопротивления. Автоматические устройства, воздействующие на управляющие органы двигателей – рычаги управления двигателями (РУД) и обеспечивающие автоматическое управление скоростью полета, называются автоматами тяги. Так как авиационный двигатель, используемый в качестве регулирующего фактора при управлении скоростью полета, формирует требуемую тягу с запаздыванием по отношению к перемещению ручки управления, то его динамические характеристики будут влиять на динамику контура управления скоростью полета. Поэтому при исследовании процессов в контуре управления скоростью полета следует учитывать запаздывание в передаче сигналов через двигатель. Для автоматического регулирования скорости полета могут быть применены статический и астатический регуляторы (рис. 2.1 и 2.2). В качестве чувствительных элементов в этих регуляторах обычно применяются аэрометрические измерители скорости полета, а сигналы ускорений могут быть получены с помощью акселерометров или дифференцирующих устройств. На этих схемах передаточная функция самолета по скорости полета отображена инерционным звеном, а передаточная функция авиадвигателя – звеном 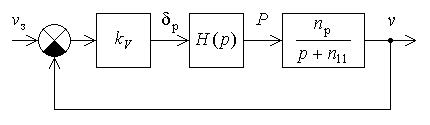 , которое в дальнейшем тоже будем считать инерционным, т.е.  , где  ,  – постоянная времени авиадвигателя. Рис. 2.1. Структурная схема статического регулирования скорости полета 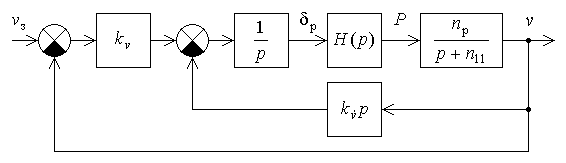 Рис. 2.2. Структурная схема астатического регулирования скорости полета При рассмотрении динамики процессов управления скоростью полета будем полагать, что угловые движения самолета стабилизируются быстродействующим автопилотом. В таком случае математическая модель самолета как объекта управления по скорости полета может быть представлена уравнением  , (2.4)где  – порывы ветра;  и  – безразмерные коэффициенты.Передаточная функция самолета по скорости полета  .Уравнения движения автоматов скорости с учетом передаточной функции авиадвигателя можно представить: – для статической  ; (2.5)– для астатической системы  , (2.6)где  и  – передаточные числа и  – сигнал заданной скорости полета.Рассмотрим переходные процессы в статическом автомате скорости полета, для чего решим совместно уравнения (2.4) и (2.5). Найдем уравнение замкнутой системы  , (2.7)где  ;  ;  ;  .Поскольку для неустойчивых по скорости полета самолетов  , то условиями устойчивости системы будут ;  . (2.8)Первое условие всегда выполняется, поскольку  . Для выполнения второго условия передаточное число должно удовлетворять условию . (2.9)В качестве примера определим значение из выражения (2.9) для сверхзвукового самолета, имеющего параметры  и  . Подставляя эти значения в условие (2.9), найдем  , т.е. для устойчивости самолета с автоматом скорости передаточное число должно быть не меньше 0,5.Выбор оптимальных значений параметров можно производить на основании приближения передаточной функции системы к стандартной передаточной функции, т.е. 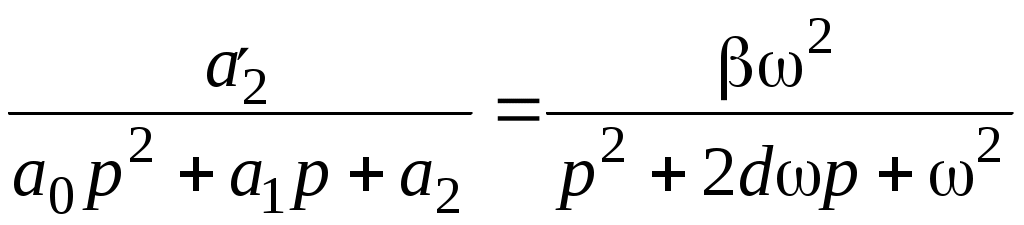 , (2.10)где  .Сравнивая коэффициенты при одинаковых степенях p в (2.10) получим  (2.11)Отс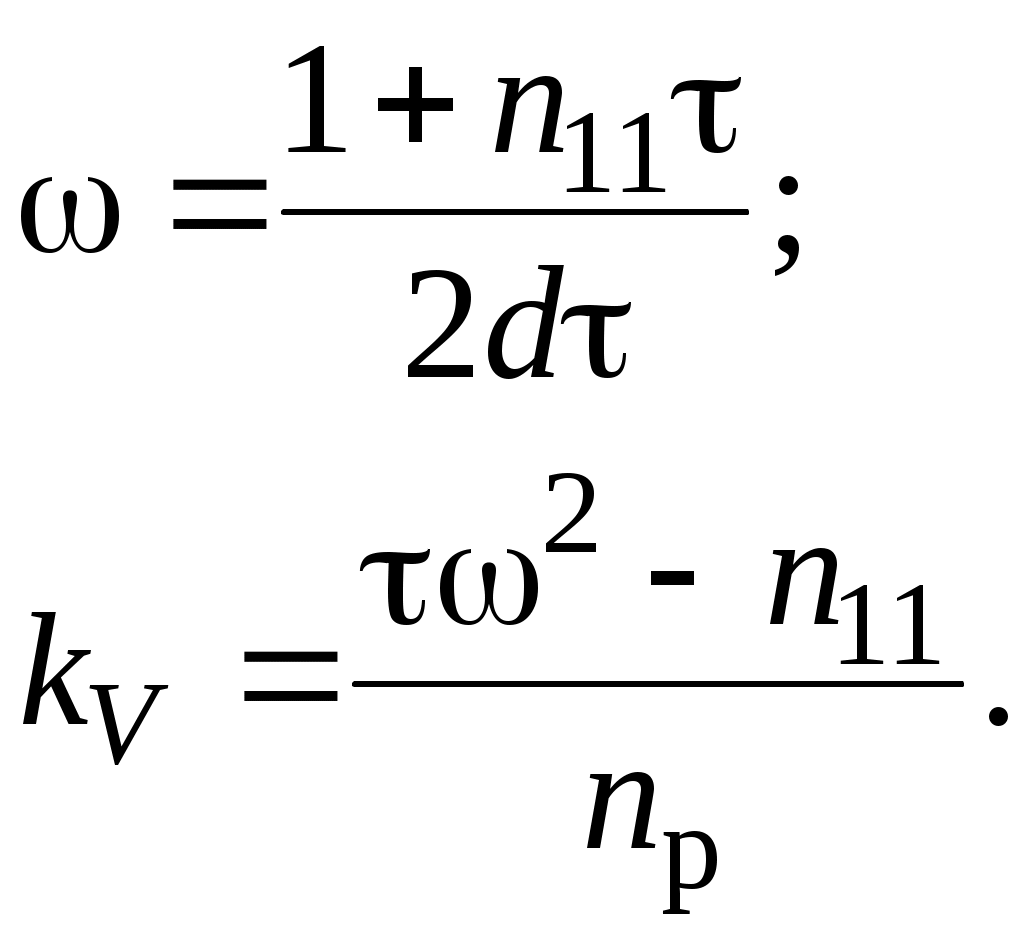юда  (2.12)В качестве примера вычислим передаточное число  для сверхзвукового самолета, неустойчивого по скорости полета и имеющего ; ;  . Постоянная времени двигателя по тяге  . Тогда  . Для случая  получаем  В случае астатического автомата скорости полета, решая совместно уравнения (2.4) и (2.6), получаем  , (2.13)где ; ;  ;  .Для устойчивости системы необходимо удовлетворить условиям: 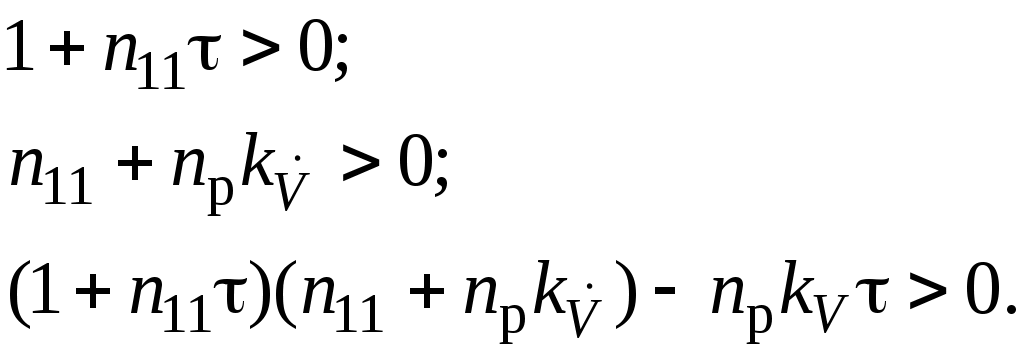 (2.14)Отсюда следует, что если  , то система структурно неустойчива.Можно выбрать такие передаточные числа и , при которых переходные процессы будут удовлетворительными.Для выбора передаточных чисел астатического автопилота запишем передаточную функцию замкнутой системы при   . (2.15)Поделим числитель и знаменатель функции  на  и приблизим полученную функцию к стандартной , (2.16)где  и  – параметры Вышнеградского, – собственная частота системы.Условия совпадения данных передаточных функций сводятся к равенствам 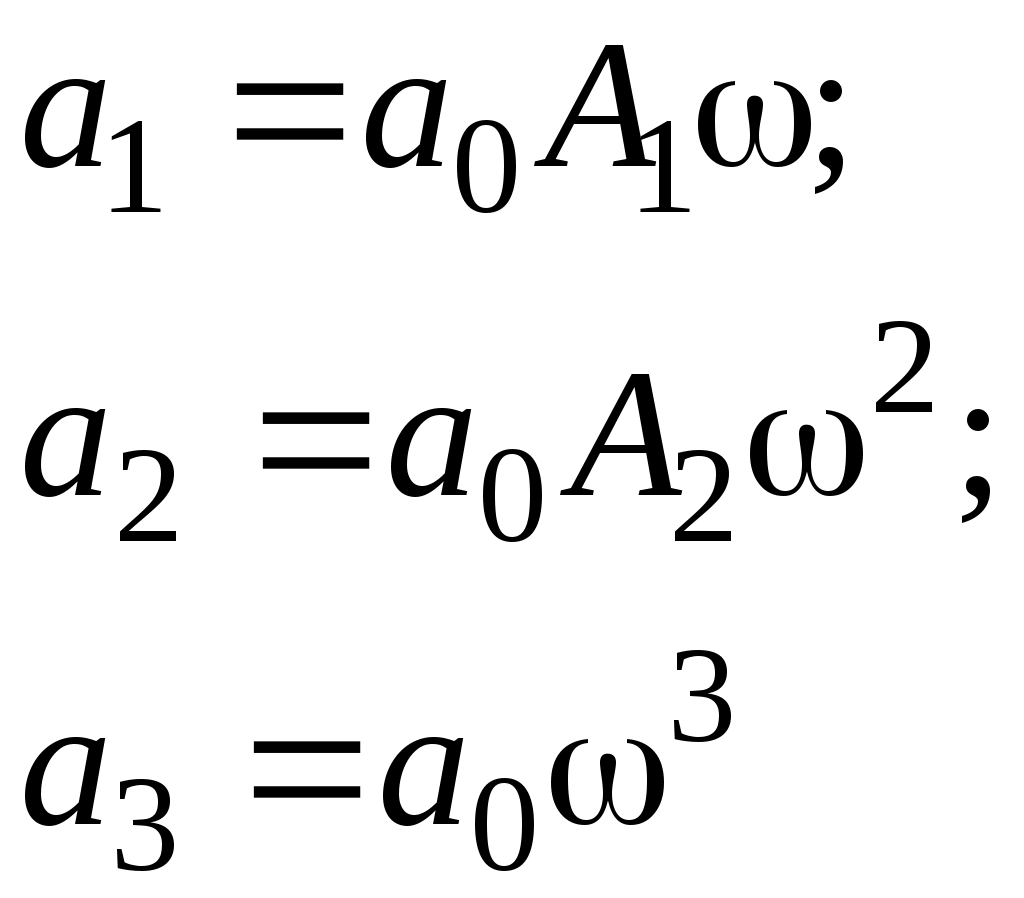 (2.17)Из уравнений (2.17) находим: 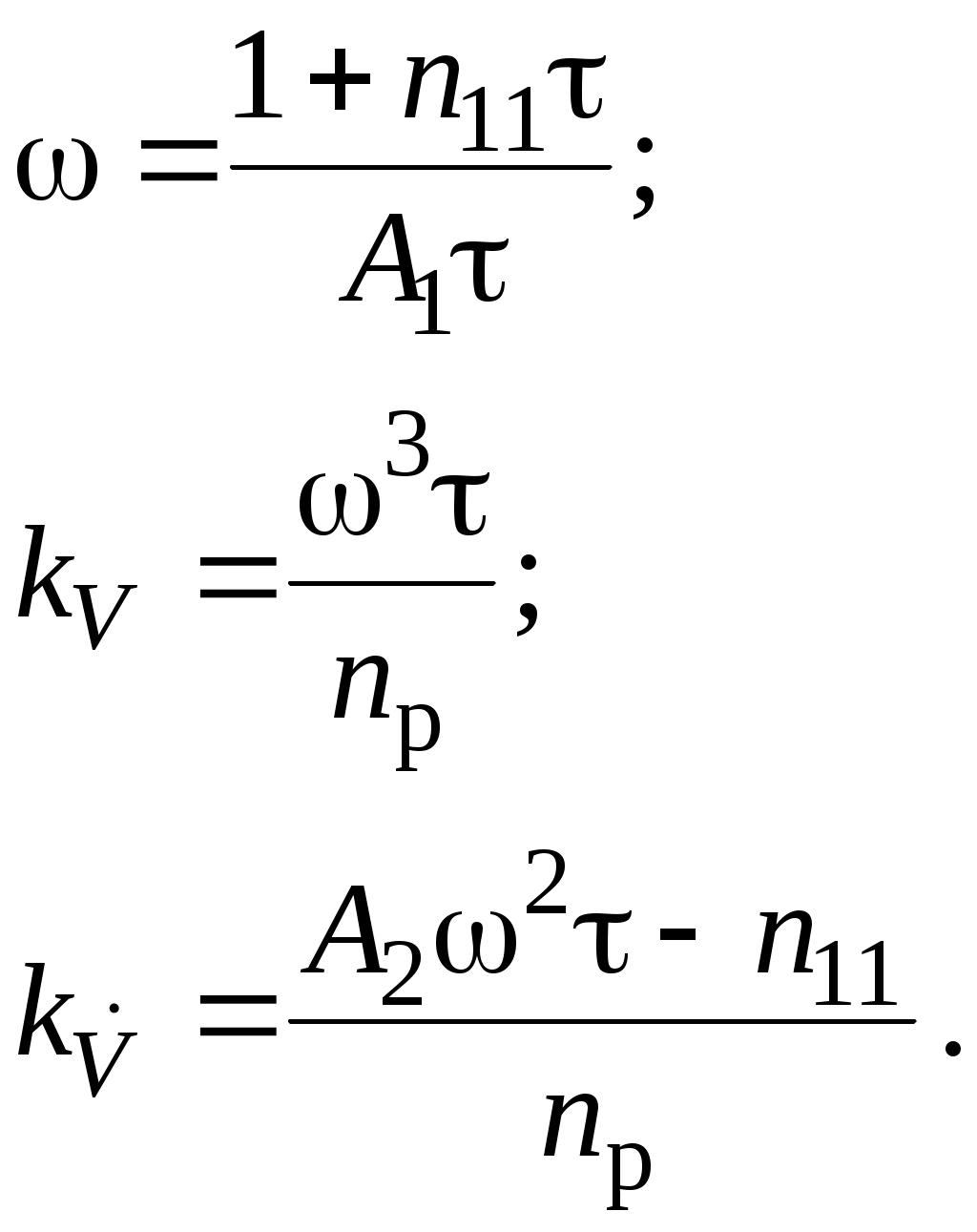 (2.18)Если принять  , то при прежних параметрах самолета и авиадвигателя получим ; ; .Полученные значения частоты и передаточных чисел и  являются безразмерными величинами.Описание автомата тяги АТ-5 в составе автоматической бортовой системы управления АБСУ-134А [7] приведено в приложении. 2.3. Задание 1. Изучить принципы построения САУ скоростью полета с использованием автомата тяги. 2. Провести анализ и синтез динамических характеристик САУ скоростью полета с использованием статического и астатического автомата тяги. 3. Экспериментально исследовать устойчивость и качество работы САУ скоростью полета с использованием автомата тяги на цифровой модели. 2.4. Описание лабораторной установкиЛабораторной установкой является ЦВМ IBM PC для проведения цифрового моделирования. При исследовании динамических характеристик САУ скоростью полета сначала проводится исследование статической системы (рис. 2.1), а затем астатической системы (рис. 2.2) при наличии и отсутствии обратной связи по ускорению. Значения основных параметров самолета приведены в таблице.
Цифровое моделирование переходных процессов, происходящих в САУ при подаче на вход единичного воздействия производится с использованием пакета SimuLink системы Matlab. Схемы моделирования приведены соответственно на рис. 2.3 и рис. 2.4. Параметры самолета задаются с помощью блока Transfer Fcn2 или Transfer Fcn3, параметры двигателя – с помощью блока Transfer Fcn1 или Transfer Fcn2. Входным сигналом САУ является единичное, ступенчатое изме-нение (блок Step). На выходе схемы с помощью блока Scope наблюдается переходной процесс по выходной координате системы  .Включение обратной связи по ускорению осуществляется при верхнем положении переключателя Manual Switch, при нижнем положении этого переключателя обратная связь отключается. 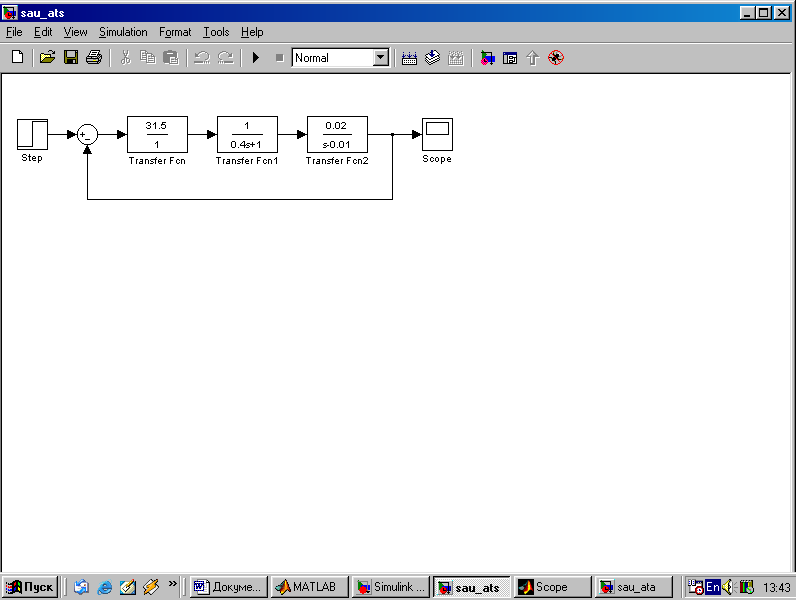 Рис. 2.3. Схема моделирования статического автомата тяги 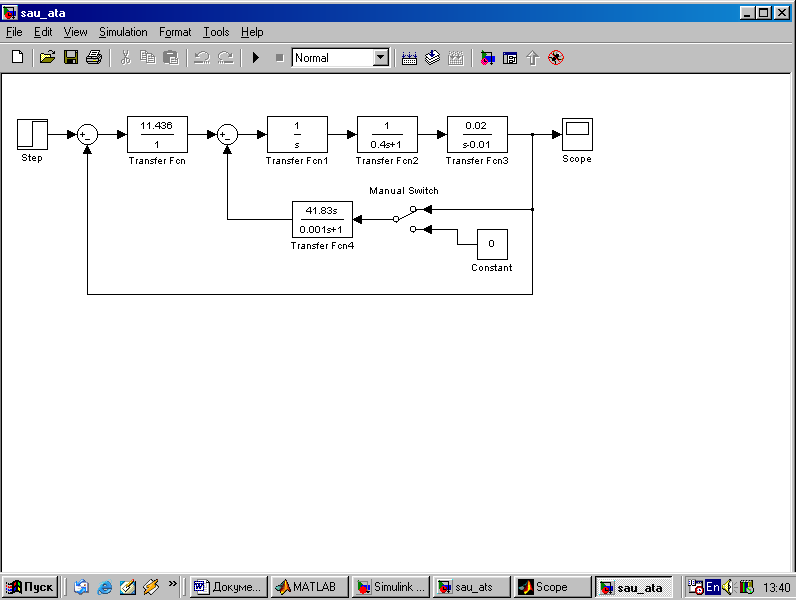 Рис. 2.4. Схема моделирования астатического автомата тяги При моделировании переходных процессов на графиках по оси абсцисс получаем значения безразмерного времени | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
. Для получения размерного (действительного) времени значения абсцисс необходимо умножить на аэродинамическую постоянную времени самолета:
.
статической и астатической САУ скоростью полета, принимая 
.