ЗАДАЧИ НА смо. стат 9. Системы массового обслуживания

• Название: Системы массового обслуживания
• Анкор: ЗАДАЧИ НА смо
• Дата: 28.12.2021
• Размер: 11.02 Kb.
• Имя файла: стат 9.docx
• Тип: Документы; #320643

Системы массового обслуживания.

Исчисляем показатели обслуживания многоканальной СМО:

Интенсивность потока обслуживания: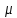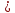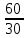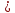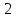



1. Интенсивность нагрузки.

ρ = λ∙t_обс = 10∙30/60 = 5

Интенсивность нагрузки ρ=5 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания.

3. Вероятность, что канал свободен (доля времени простоя каналов).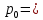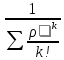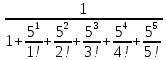



Следовательно, 1.09% в течение часа канал будет не занят, время простоя равно t_пр = 0.7 мин.

Вероятность того, что обслуживанием:

занят 1 канал:

p₁ = ρ¹/1! p₀ = 5¹/1!∙0.0109 = 0.0547

заняты 2 канала:

p₂ = ρ²/2! p₀ = 5²/2!∙0.0109 = 0.137

заняты 3 канала:

p₃ = ρ³/3! p₀ = 5³/3!∙0.0109 = 0.228

заняты 4 канала:

p₄ = ρ⁴/4! p₀ = 5⁴/4!∙0.0109 = 0.285

заняты 5 канала:

p₅ = ρ⁵/5! p₀ = 5⁵/5!∙0.0109 = 0.285

4. Вероятность отказа (вероятность того, что канал занят) (доля заявок, получивших отказ).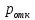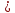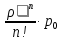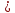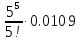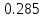



Значит, 29% из числа поступивших заявок не принимаются к обслуживанию.

5. Вероятность обслуживания поступающих заявок (вероятность того, что клиент будет обслужен).

В системах с отказами события отказа и обслуживания составляют полную группу событий, поэтому: p_отк + p_обс = 1

Относительная пропускная способность: Q = p_обс.

p_обс = 1 - p_отк = 1 - 0.285 = 0.715

Следовательно, 72% из числа поступивших заявок будут обслужены. Приемлемый уровень обслуживания должен быть выше 90%.

6. Среднее число каналов, занятых обслуживанием (Среднее число занятых каналов).

n_з = ρ∙p_обс = 5∙0.715 = 3.576 канала.

Среднее число простаивающих каналов.

n_пр = n - n_з = 5 - 3.576 = 1.4 канала.

7. Коэффициент занятости каналов обслуживанием.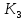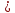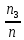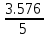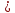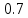



Следовательно, система на 70% занята обслуживанием.

8. Абсолютная пропускная способность (Интенсивность выходящего потока обслуженных заявок).

A = p_обс∙λ = 0.715∙10 = 7.151 заявок/час.

9. Среднее время простоя СМО ( час.).

t_пр = p_отк∙t_обс = 0.285∙0.5 = 0.142

10. Среднее время простоя канала ( час.).

t_п.к. = t_обс∙(1-p_отк)/p_отк = 0.5∙(1-0.285)/0.285 = 5.021

12. Среднее число обслуживаемых заявок.

L_обс = ρ∙Q = 5∙0.715 = 3.576 ед.

14. Среднее время пребывания заявки в СМО (формула Литтла).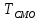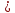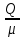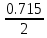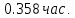



Число заявок, получивших отказ в течение часа: λ∙p₁ = 2.85 заявок в час.

Номинальная производительность СМО: 5 / 0.5 = 10 заявок в час.

Фактическая производительность СМО: 7.151 / 10 = 72% от номинальной производительности.

Определим количество каналов, необходимых для обеспечения работоспособности системы с вероятностью P ≥ 0.9

Для этого находим n из условия: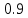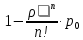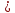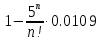


Решение было получено и оформлено с помощью сервиса:

Многоканальные СМО

Вместе с этой задачей решают также:

Параметры сетевого графика

Линейное программирование онлайн

Динамическое программирование

Теория игр онлайн