Системы счисления. Двоичная система счисления.. Системы счисления. Двоичная система счисления
 Скачать 19.15 Kb. Скачать 19.15 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «Алтайский государственный педагогический университет» Доклад Тема: «Системы счисления. Двоичная система счисления» Выполнил студент группы 3713з Сухов Руслан Александрович Виды систем счисленияСистема счисления – это способ записи (изображения) чисел.Различные системы счисления, которые существовали раньше и которые используются в настоящее время, делятся на две группы:позиционные,непозиционные.Наиболее совершенными являются позиционные системы счисления. Они являются результатом длительного исторического развития непозиционных систем счисления. Цель создания системы счисления- выработка наиболее удобного способа записи количественной информации. Существует много различных систем счисления. Некоторые из них распространены, другие распространения не получили. Наиболее простая и понятная для нас система счисления - десятичная (основание 10). Понятна она потому, что мы используем ее в повседневной жизни. Позиционные и непозиционные системы счисленияРазнообразные системы счисления, которые существовали раньше и которые используются в наше время, можно разделить на непозиционные и позиционные. Знаки, используемые при записи чисел, называются цифрами. В непозиционных системах счисления от положения цифры в записи числа не зависит величина, которую она обозначает. Примером непозиционной системы счисления является римская система, в которой в качестве цифр используются латинские буквы. В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от ее позиции. Количество используемых цифр называется основанием системы счисления. Место каждой цифры в числе называется позицией. Первая известная нам система, основанная на позиционном принципе – шестидесятеричная вавилонская. Цифры в ней были двух видов, одним из которых обозначались единицы, другим – десятки. В настоящее время позиционные системы счисления более широко распространены, чем непозиционные. Это объясняется тем, что они позволяют записывать большие числа с помощью сравнительно небольшого числа знаков. Еще более важное преимущество позиционных систем - это простота и легкость выполнения арифметических операций над числами, записанными в этих системах. Запись числа в позиционной системе счисленияОснование системы счисления, в которой записано число, обычно обозначается нижним индексом. Например, 5557 – число, записанное в семеричной системе счисления. Если число записано в десятичной системе, то основание, как правило, не указывается. Основание системы – это тоже число, и его указывают в обычной десятичной системе. Любое целое число в позиционной системе можно записать в форме многочлена: Хs={AnAn-1An-2...A2A1}s =An·Sn-1+An-1·Sn-2+An-2·Sn-3+...+A2·S1+A1·S0 где S - основание системы счисления, Аn - цифры числа, записанного в данной системе счисления, n - количество разрядов числа. Так, например число 629310 запишется в форме многочлена следующим образом: 629310=6·103 + 2·102 + 9·101 + 3·100 Примеры позиционных систем счисленияДвоичная (или система счисления с основанием 2) это положительная целочисленная позиционная (поместная) система счисления, позволяющая представить различные численные значения с помощью двух символов. Чаще всего это 0 и 1. Восьмеричная — позиционная целочисленная система счисления с основанием 8. Для представления чисел в ней используются цифры 0 до 7. Восьмеричная система часто используется в областях, связанных с цифровыми устройствами. Ранее широко использовалась в программировании и компьютерной документации, однако в настоящее время почти полностью вытеснена шестнадцатеричной. Десятичная система счисления — позиционная система счисления по целочисленному основанию 10. Наиболее распространённая система счисления в мире. Для записи чисел наиболее часто используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называемые арабскими цифрами. Шестнадцатеричная (наиболее распространена в программировании, а также в шрифтах) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15. Широко используется в низкоуровневом программировании и вообще в компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. История двоичной системыДвоичная система счисления была придумана математиками и философами ещё до появления компьютеров (XVII — XIX вв.). Некоторые идеи, лежащие в основе двоичной системы, по существу были известны в Древнем Китае. Об этом свидетельствует классическая книга “И цзин” (“Книга перемен”). Пропагандистом двоичной системы был знаменитый Г.В. Лейбниц (получивший, от Петра I звание тайного советника). Он отмечал особую простоту алгоритмов арифметических действий в двоичной арифметике в сравнении с другими системами и придавал ей определенный философский смысл. Говорят, что по его предложению была выбита медаль с надписью: “Для того чтобы вывести из ничтожества все, достаточно единицы”. Известный современный математик Т.Данциг о нынешнем положении дел сказал: “Увы! То, что некогда возвышалось как монумент монотеизму, очутилось в чреве компьютера”. Потом о двоичной системе забыли. В течение почти 200 лет на эту тему не было издано ни одного труда. Вернулись к ней только в 1931 году, когда были продемонстрированы некоторые возможности практического применения двоичного счисления. В 1936 — 1938 годах американский инженер и математик Клод Шеннон нашёл замечательные применения двоичной системы при конструировании электронных схем. Двоичная система счисленияДвоичная система счисления (Бинарная система счисления, binary) - позиционная система счисления с основанием 2. Для представления чисел используются символы 0 и 1. Главное достоинство двоичной системы — простота алгоритмов сложения, вычитания, умножения и деления. Таблица умножения в ней совсем не требует ничего запоминать: ведь любое число, умноженное на ноль, равно нулю, а умноженное на единицу равно самому себе. И при этом никаких переносов в следующие разряды, а они есть даже в троичной системе. Рассмотрим подробнее, как происходит процесс умножения двоичных чисел. Пусть надо умножить число 1101 на 101 (оба числа в двоичной системе счисления). Машина делает это следующим образом: она берет число 1101 и, если первый элемент второго множителя равен 1, то она заносит его в сумму. Затем сдвигает число 1101 влево на одну позицию, получая тем самым 11010, и если, второй элемент второго множителя равен единице, то тоже заносит его в сумму. Если элемент второго множителя равен нулю, то сумма не изменяется. Таблица деления сводится к двум равенствам 0/1 = 0, 1/1 = 1, благодаря чему деление столбиком многозначных двоичных чисел делается гораздо проще, чем в десятичной системе и, по существу, сводится к многократному вычитанию. Выполнение основной процедуры - выбор числа, кратного делителю и предназначенного для уменьшения делимого, здесь проще, так как таким числом могут быть либо 0, либо сам делитель. Сложение многоразрядных двоичных чисел осуществляется в соответствии с таблицей с учетом возможных переносов из младшего разряда в старшие. Вот как выглядит таблица сложения в двоичной системе:
При выполнении операции вычитания всегда из большего по абсолютной величине числа вычитается меньшее и у результата ставится соответствующий знак. Таблица разности двоичных чисел:
Недостатком двоичной системы является то, что она не привычна для человека. Значит, неудобством этой системы счисления (как, впрочем, и всякой другой, отличной от десятичной) является необходимость перевода исходных данных из десятичной системы в двоичную при вводе их в машину и обратного перевода из двоичной в десятичную при выводе результатов вычислений. Перевод двоичного числа в десятичноеДля перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики: Х2= Аn·2n-1 + Аn-1·2n-2 + Аn-2·2n-3 +…+А2·21 + А1·20 При переводе удобно пользоваться таблицей степеней двойки:
Пример: Число 111010002 перевести в десятичную систему счисления: 111010002= 1·27 + 1·26 + 1·25 +0·24 + 1·23+0·22+0·21+0·20=23210 Перевод десятичного числа в двоичную системуДля перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке. Пример: Число 2210 перевести в двоичную систему счисления: 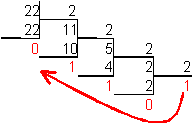 2210=101102 Двоичное кодирование в компьютере В конце ХХ века, века компьютеризации, человечество пользуется двоичной системой ежедневно, так как вся информация, обрабатываемая современными ЭВМ, хранится в них в двоичном виде. Каким же образом осуществляется это хранение? Каждый регистр арифметического устройства ЭВМ, каждая ячейка памяти представляют собой физическую систему, состоящую из некоторого числа однородных элементов. Любой такой элемент способен находиться в нескольких состояниях и служит для изображения одного из разрядов числа. Именно поэтому каждый элемент ячейки называют разрядом. Нумерацию разрядов в ячейке принято вести справа налево, самый левый разряд имеет порядковый номер 0. Если при записи чисел в ЭВМ мы хотим использовать обычную десятичную систему счисления, то мы должны двоичное кодирование информации уметь получать 10 устойчивых состояний для каждого разряда (как на счетах при помощи костяшек). Такие машины существуют. Однако конструкция элементов такой машины оказывается чрезвычайно сложной, что сказывается на надежности и скорости работы ЭВМ. Наиболее надежным и дешевым является устройство, каждый разряд которого может принимать два состояния: намагничено – не намагничено, высокое напряжение – низкое напряжение и т.д. В современной электронике развитие аппаратной базы ЭВМ идет именно в этом направлении. Следовательно, использование двоичной системы счисления в качестве внутренней системы представления информации вызвано конструктивными особенностями элементов вычислительных машин. В современные компьютеры мы можем вводить текстовую информацию, числовые значения, а также графическую и звуковую информацию. Количество информации, хранящейся в ЭВМ, измеряется ее «длиной» (или «объемом»), которая выражается в битах (от английского binary digit – двоичная цифра). Бит – минимальная единица измерения информации. В каждом бите может храниться 0 или 1. |
