Система Счислений. Лекция 5. Системы счисления и их разновидности
 Скачать 205.68 Kb.
|
Системы счисления и их разновидности.Система счисления – это способ представления, записи чисел с помощью письменных знаков. Количество этих самых знаков (цифр), используемых для записи чисел, называется основанием системы счисления. Различных систем счисления у разных народов существовало великое множество. Но все их можно поделить на непозиционные и позиционные. Позиционные системы в свою очередь подразделяются на однородные и смешанные. 1. Непозиционные системы счисления. В непозиционных системах счисления число, обозначаемое цифрой, не зависит от положения цифры в записи числа. Самым простым примером непозиционной системы счисления является единичная (унарная) система счисления. Это запись числа с помощью повторения зарубок на дощечке или узелков на веревке. Все зарубки, узелки или другие «цифры» абсолютно одинаковы, а потому их порядок не имеет значения, число получается простым суммированием количества символов.   Унарной системой счисления до сих пор пользуются маленькие дети, показывая количество на пальцах. Еще одной используемой до сих пор почти непозиционной системой счисления является Римская:        Она названа почти непозиционной, потому что в Римской системе, кроме обычного сложения цифр в числе, действует правило: если младшая цифра стоит слева от старшей, она вычитается из суммы. Т.е. число  , а число  Непозиционных систем счисления известно очень много, но мы завершим на этом их рассмотрение. Использование непозиционных систем неудобно, а для очень больших чисел практически невозможно, и к тому же нет возможности записать дроби. 2. Позиционные системы счисления. В позиционных системах счисления число, обозначаемое цифрой, зависит от положения цифры в записи числа. Самой популярной позиционной системой является, конечно же, десятичная. Мы видим, что числа 15 и 51 имеют совсем разные значения, хотя состоят из одних и тех же цифр. Разница обусловлена положением цифры в числе. Но десятичная система ничем не лучше и не хуже другой позиционной системы, она просто привычная. Число 10 выбрано основанием по количеству пальцев на двух руках (для удобства счета). Однако, в Китае популярной была пятиречная система счисления (по количеству пальцев на одной руке), а двадцатиричная система использовалась у Ацтеков, Майя и некоторых народов Африки (по количеству пальцев на ногах и руках). Еще одной известной позиционной системой счисления является двенадцатиричная (считали фаланги пальцев (кроме большого) на руке. Элементы двенадцатиричной системы сохранились в Англии: 1 фут = 12 дюймов, 1 шиллинг = 12 пенсов. 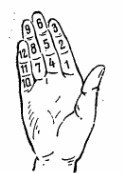 Ну и, наконец, незаменимая в наш компьютерный век двоичная система. Почему именно двоичная? Да потому что у компьютера только 2 «пальца», точнее два состояния: «есть ток», «нет тока». 2.1. Однородные системы счисления. В однородной системе в каждой позиции числа может находиться любая цифра. Примером может быть запись числа в любой позиционной системе счисления (десятичной, двоичной и пр.). Т.е. когда мы пишем число в десятичной системе, в любой позиции мы можем написать цифру от 0 до 9. 2.2. Смешанные системы счисления. В смешанной системе счисления набор используемых цифр может отличаться в зависимости от позиции. В качестве примера удобно рассмотреть запись времени в формате ЧЧ.ММ.СС (часы.минуты.секунды). В качестве часов может быть использовано число от 00 до 23, в качестве минут и секунд – число от 00 до 59. Системы счисления. Перевод из одной системы в другую.1. Порядковый счет в различных системах счисления. В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные». Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы. Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее. Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение  для 2-ной системы,  для 3-ной и т.д.):
Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы (  и  ):
2.Перевод из десятичной системы счисления в любую другую. Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего. Пример 1. Переведем десятичное число 46 в двоичную систему счисления. 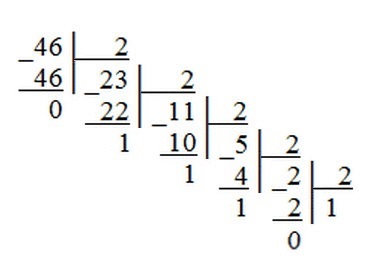  Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления. 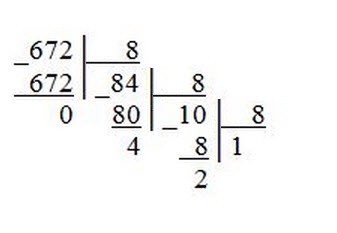  Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления. 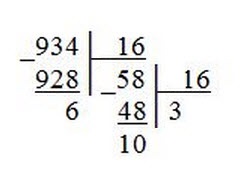  3. Перевод из любой системы счисления в десятичную. Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа. Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.  Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:    Это и есть десятичная запись нашего числа, т.е.  Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.   Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.   4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.). Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления. Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к.  ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:
Таблицу соответствия мы научились строить в п.1.
Т.е.  Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.
 5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную. Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия. Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления. Для этого каждую цифру числа заменим группой из 4 цифр (т.к.  ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:     Десятичные дроби и смешанные числа в разных системах счисления.Перевод целых чисел из одной системы счисления в другую обычно не вызывает проблем. А вот необходимость перевести десятичную дробь или смешанное число (число с целой и дробной частью) из системы в систему часто ставит в тупик даже сильных учеников. 1. Перевод смешанного числа в десятичную систему счисления из любой другой. Для перевода смешанного числа в десятичную систему из любой другой следует пронумеровать разряды числа, начиная с нуля, справа налево от младшего целого разряда. Разряды дробной части нумеруются слева направо от -1 в убывающем порядке. Теперь представим число в виде суммы произведений его цифр на основание системы в степени разряда числа и ответ готов. Пример 1. Переведите число 105,4 из восьмеричной системы в десятичную. Решение: Пронумеруем целые разряды числа справа налево от 0, дробные – слева направо от -1 :  Посчитаем сумму произведений цифр числа на 8 (основание системы) в степени разряда числа:  Ответ:  2. Перевод десятичных дробей из десятичной системы счисления в любую другую. Для перевода десятичной дроби из десятичной системы в любую другую следует умножать дробь, а затем дробные части произведений, на основание новой системы пока дробная часть не станет равной 0 или до достижения указанной точности. Затем целые части выписать, начиная с первой. Пример 2 Переведите десятичное число 0,816 в двоичную систему с точностью до сотых. Решение: Умножаем дробь 0,816, а затем дробную часть произведения (0,632) на 2 и выписываем целые части, начиная с первой: 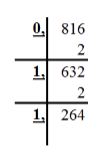  Ответ:  Пример 3. Переведите десятичное число 0,8125 в восьмеричную систему. Решение: Умножаем дробь 0,8125, а затем дробную часть произведения (0,5) на 8 и выписываем целые части, начиная с первой: 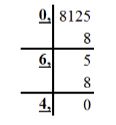  Ответ:  3. Перевод смешанных чисел из десятичной системы счисления в любую другую Если необходимо перевести смешанное число из десятичной системы в любую другую, следует перевести целую и дробную части, а затем записать, разделив десятичной запятой. Пример 4. Сколько единиц в двоичной записи десятичного числа 14,125? Решение: Переведем целую часть числа в двоичную систему: 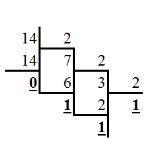 Переведем дробную часть числа в двоичную систему: 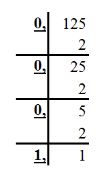 Соединим целую и дробную части:  14,12510 = 1110,0012 |
