ОЦОСи РГР1 (89). Системы счисления. Спектральное представление сигналов Специальность Радиотехника, электроника и телекоммуникации
 Скачать 163.79 Kb. Скачать 163.79 Kb.
|
|
Некоммерческое акционерное общество «АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ» Кафедра Телекоммуникационных систем Дисциплина Основы цифровой обработки сигналов в телекоммуникационных системах РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №1 На тему: «Системы счисления. Спектральное представление сигналов» Специальность: Радиотехника, электроника и телекоммуникации Выполнил: Турекешев Ч. Группа: РЭТ-13-6 № зач. книжки:133289 Проверила: ст.преп. Богомолова Л.Г. __________________________ «____» _____________________201___г. Алматы 2016 СОДЕРЖАНИЕ Введение 4 ЗАДАЧА 1. СИСТЕМЫ СЧИСЛЕНИЯ 5 1.1 Условие задачи 1. Исходные данные 5 1.2 Выполнение задания 1 6 1.2.1 Перевод в двоичную систему счисления 6 1.2.2 Перевод в восьмеричную систему счисления 6 1.2.3 Перевод в шестнадцатеричную систему счисления 7 1.2.4 Обратное преобразование 7 В этой записи а0, а1, … обозначают цифры нулевого, первого и т. д. разрядов числа. Цифре разряда приписан вес pk, где p – основание системы счисления, k – номер разряда, равный индексу при обозначениях цифр разрядов. Перевод из двоичной системы счисления: 7 Перевод из восьмеричной системы счисления: 7 Перевод из шестнадцатеричной системы счисления: 7 По результатам расчета видно, что при прямом преобразовании с увеличением основания новой системы длина записи уменьшается. Самой громоздкой оказывается запись в двоичной системе счисления, а самой удобной и короткой в шестнадцатеричной. Обратный же перевод проще осуществить при использовании двоичной системы счисления. 7 2.1 Условие задачи 2. Исходные данные 8 2.2 Выполнение задания 2 9 2.2.1 Математическая модель импульса 9 2.2.2 Спектральная плотность импульса 9 2.2.3 АЧХ и ФЧХ спектральной плотности 10 2.2.4 Дискретизация сигнала 11 2.2.5 Математическая модель дискретизованного сигнала 12 12 2.2.6 Спектральная плотность дискретизованного сигнала 13 2.2.7 Амплитудный спектр дискретизованного сигнала 13 Список литературы 16 Введение 4 ЗАДАЧА 1. СИСТЕМЫ СЧИСЛЕНИЯ 5 1.1 Условие задачи 1. Исходные данные 5 1.2 Выполнение задания 1 6 1.2.1 Перевод в двоичную систему счисления 6 1.2.2 Перевод в восьмеричную систему счисления 6 1.2.3 Перевод в шестнадцатеричную систему счисления 7 1.2.4 Обратное преобразование 7 В этой записи а0, а1, … обозначают цифры нулевого, первого и т. д. разрядов числа. Цифре разряда приписан вес pk, где p – основание системы счисления, k – номер разряда, равный индексу при обозначениях цифр разрядов. Перевод из двоичной системы счисления: 7 Перевод из восьмеричной системы счисления: 7 Перевод из шестнадцатеричной системы счисления: 7 По результатам расчета видно, что при прямом преобразовании с увеличением основания новой системы длина записи уменьшается. Самой громоздкой оказывается запись в двоичной системе счисления, а самой удобной и короткой в шестнадцатеричной. Обратный же перевод проще осуществить при использовании двоичной системы счисления. 7 2.1 Условие задачи 2. Исходные данные 8 2.2 Выполнение задания 2 9 2.2.1 Математическая модель импульса 9 2.2.2 Спектральная плотность импульса 9 2.2.3 АЧХ и ФЧХ спектральной плотности 10 2.2.4 Дискретизация сигнала 11 2.2.5 Математическая модель дискретизованного сигнала 12 12 2.2.6 Спектральная плотность дискретизованного сигнала 13 2.2.7 Амплитудный спектр дискретизованного сигнала 13 Список литературы 16 ВведениеСистемой счисления называют систему приемов и правил, которые позволяют устанавливать взаимно однозначное соответствие между любым числом и его представлением в виде совокупности конечного числа символов. Системы счисления делятся на непозиционные и позиционные. В непозиционной системе значение каждого символа постоянно, где бы символ ни находился в числе (например, римская система).В позиционной системе значение каждого символа зависит от места в числе, где записан этот символ (например, арабская система). Из позиционных систем счисления широко распространена десятичная система, которая используется в нашей повседневной жизни. Для мира цифровой техники наибольший интерес представляет двоичная система. Цифровые устройства используют элементы, которые имеют только два устойчивых состояния, поэтому для представления и обработки информации удобно применение именно данной системы счисления. При работе с цифровыми устройствами гораздо удобнее работать со спектрами, то есть в частотной области. Это позволяет упростить оборудование и сократить время обработки сигнала. Переход из временной области в частотную осуществляют с помощью прямого преобразования Фурье. Оно является взаимно – однозначным, поэтому представление сигнала в частотной области (спектр) содержит ровно столько же информации, сколько и исходный сигнал, заданный во временной области. Преобразование Фурье является инструментом спектрального анализа непериодических сигналов, но можно применять и к сигналам периодическим, но для этого потребуется использование аппарата обобщенных функций. Изменение пределов интегрирования не играет роли – ведь на добавившемся между импульсами пространстве сигнал имеет нулевое значение. Единственное дополнительное изменение будет состоять в уменьшении общего уровня гармоник из-за деления результата интегрирования на увеличившийся период. С ростом следования импульсов гармоники располагаются ближе друг другу по частоте, а общий уровень спектральных составляющих становится все меньше. ЗАДАЧА 1. СИСТЕМЫ СЧИСЛЕНИЯ1.1 Условие задачи 1. Исходные данныеПровести следующие операции с числом, образованным номером зачетной книжки: а) перевести в двоичную систему; б) перевести в восьмеричную систему; б) перевести в шестнадцатеричную систему; в) перевести в десятичную систему числа, полученные в двоичной системе, восьмеричной системе, шестнадцатеричной системе, то есть сделать обратное преобразование. Исходные данные: № зачетной книжки: 133289 1.2 Выполнение задания 1При прямом преобразовании производят последовательное деление десятичного числа и образующихся частных на основание системы счисления до тех пор, пока остаток от деления не будет меньше основы системы. Полученные при делении остатки образуют цифры всех разрядов числа, представленного в нужной системе счисления. Число в новой системе записывается в виде остатков от деления, начиная с последнего остатка справа налево. 1.2.1 Перевод в двоичную систему счисления133289|2_____ 133288| 66644|2___ 1 66644| 33322| 2____ 0 33322| 16661| 2____ 0 16660| 8330| 2____ 1 8330| 4165|2__ 0 4164|2082| 2__ 1 2082| 1041| 2__ 0 1040| 520| 2__ 1 520| 260| 2_ 0 260| 130| 2_ 0 130| 65| 2_ 0 64| 32| 2_ 1 32| 16| 2_ 0 16| 8| 2 0 8| 4| 2 0 4| 2| 2 0 2| 1 0 13328910 = 1000001000101010012 1.2.2 Перевод в восьмеричную систему счисления133289|8_ 133288| 16661|8__ 1 16656| 2082|8_ 5 2080| 260| 8_ 2 256| 32| 8 4 32| 4 0 13328910 = 4042518 1.2.3 Перевод в шестнадцатеричную систему счисления133289|16___ 133280| 8330|16_ 9 8320| 520|16_ A 512| 32|16 8 32| 2 0 13328910 = 208A916 1.2.4 Обратное преобразованиеПри обратном преобразовании числа в рассматриваемых системах счисления представляют собой последовательность цифр (цифр разрядов): …а2а1а0 В этой записи а0, а1, … обозначают цифры нулевого, первого и т. д. разрядов числа. Цифре разряда приписан вес pk, где p – основание системы счисления, k – номер разряда, равный индексу при обозначениях цифр разрядов. Перевод из двоичной системы счисления: 1000001000101010012 = 1·217 + 0·216 + 0·215 + 0·214 + 0·213 + 0·212 + 1·211 + 0·210 + 0·29 + 0·28 + 1·27 + 0·26 + 1·25 + 0·24 + 1·23 + 0·22 + 0·21 + 1·20 = 131072 + 2048 + 128 + 32 + 8 + 1 = 13328910 Перевод из восьмеричной системы счисления: 4042518 = 4·85 + 0·84 + 4·83 + 2·82 + 5·81 + 1·80 = 131072 + 2048 + 128 + 40 + 1 = 13328910 Перевод из шестнадцатеричной системы счисления: 208A916 = 2·164 + 0·163 + 8·162 + 10·161 + 9·160 = 131072 + 2048 + 160 + 9 = 13328910 2 ЗАДАЧА 2. СПЕКТРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ СИГНАЛОВ 2.1 Условие задачи 2. Исходные данныеЗадан импульс. Требуется: а) записать математическую модель (формулу), соответствующую импульсу, согласно варианту; б) определить спектральную плотность импульса, заданного в таблице, согласно варианту; в) построить АЧХ и ФЧХ спектральной плотности при заданной длительности импульса, амплитуде и других параметрах; г) используя полученные графики, построить АЧХ и ФЧХ для импульса вдвое меньшей длительности. Отобразить на графиках влияние задержки импульса на время τи; д) дискретизовать заданный сигнал с шагом Т; е) записать математическую модель (формулу) дискретизованного сигнала; ж) найти спектральную плотность дискретизованного сигнала; з) построить амплитудный спектр дискретизованного сигнала; и) расчет спектральной плотности импульса и построение АЧХ и ФЧХ импульса и амплитудного спектра дискретизованного сигнала произвести на ЭВМ.
Вид импульса приведен на рисунке 1 U0 = 1 В, Длительность импульса τи = 1 мкс, α = 3 рад/с, Шаг дискретизации T=0,05мкс 2.2 Выполнение задания 22.2.1 Математическая модель импульсаЗаданный импульс описывается формулой:  Подставив значения в (2.1), получим: 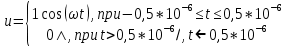 2.2.2 Спектральная плотность импульсаДля определения спектральной плотности импульса воспользуемся прямым преобразованием Фурье:  Т.к.  , то распишем интеграл: , то распишем интеграл: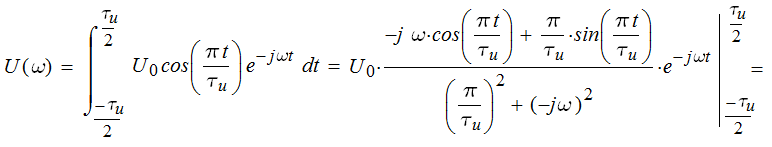 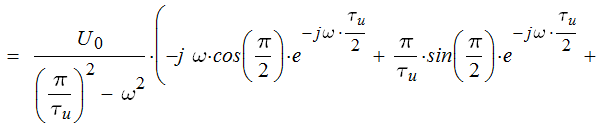  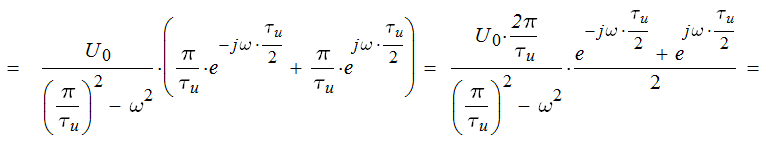 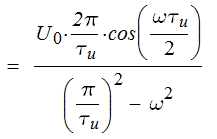 Подставим числовые значения:  2.2.3 АЧХ и ФЧХ спектральной плотностиАЧХ спектральной плотности при заданной длительности импульса, амплитуде и других параметрах U(ω) и импульса вдвое меньшей длительности U1(ω) приведены на рисунке 2. Из графиков видно, что с уменьшением длительности импульса в 2 раза ширина спектра становится примерно вдвое больше. Также происходит уменьшение амплитуды спектра в два раза.  Рисунок 2 – АЧХ спектральной плотности импульса. U(ω) – при заданной длительности, U1(ω) – вдвое меньшей длительности. ФЧХ спектральной плотности:  Рисунок 3 – ФЧХ спектральной плотности импульса. U(ω) – при заданной длительности, U1(ω) – вдвое меньшей длительности. График показывает, что с уменьшением длительности импульса ФЧХ становится шире. 2.2.4 Дискретизация сигналаДискретизируем сигнал с шагом Т = 0,05 мкс. Полное число отсчетов: N = τи/T. Подставим числа в (5): N = 1·10-6/(0,05·10-6) = 20. Круговая частота дискретизации связана с шагом дискретизации: ωд = 2π/Т. ωд = 2·3,14/(0,05·10-6) = 125,6·106, рад/с. Дискретизованный сигнал:  Рисунок 7 – Дискретизированный сигнал 2.2.5 Математическая модель дискретизованного сигнала |




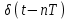
 ,
, δ(t +20T) +
δ(t +20T) +  копий спектра исходного непрерывного сигнала u(t).
копий спектра исходного непрерывного сигнала u(t).

