анализ. Системный анализ. Системный анализ, управление и обработка информации Основные понятия Система
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
|
Системный анализ, управление и обработка информации Основные понятия Система – объект или процесс, в котором элементы-участники связаны некоторыми связями и отношениями. Подсистема – часть системы с некоторыми связями и отношениями. Любая система состоит из подсистем, подсистема любой системы может быть сама рассмотрена как система. Границы рассматриваемой системы определяются доступными ресурсами и окружением. Проблема – описание, хотя бы содержательное, ситуации, в которой определены: цель, достигаемые (достижимые, желательные) результаты и, возможно, ресурсы и стратегия достижения цели (решения). Проблема проявляется поведением системы. Деятельность (работа) системы может происходить в двух основных режимах: развитие (эволюция) и функционирование. Функционированием называется деятельность, работа системы без смены (главной) цели системы. Это проявление функции системы во времени. Развитием называется деятельность системы со сменой цели системы. При функционировании системы явно не происходит качественного изменения инфраструктуры системы; при развитии системы ее инфраструктура качественно изменяется. Развитие – борьба организации и дезорганизации в системе, она связана с накоплением и усложнением информации, ее организации. Под устойчивостью системы понимается ее способность под действием входного сигнала переходить из одного состояния равновесия в другое. Понятие устойчивости связано с величиной воздействия, вызвавшего изменения состояния системы. Надо учитывать предельное значение входного сигнала. Принцип управляемости выражает необходимость зависимости показателя эффективности, целевой функции от параметров управления системой (входных сигналов). Достижимость означает что параметры, как самой системы, так и ее среды должны достичь определенных значений. Обратная связь означает получение информации о результате управления. Обратная связь может быть отрицательной и положительной. Отрицательная обратная связь характеризуется тем, что выходной сигнал, воздействующий на вход системы, имеет противоположный знак по отношению к входному, вызывающему изменение состояния системы. Системы с отрицательной обратной связью обычно предназначены для поддержания ее в устойчивом состоянии. Положительная обратная связь характеризуется тем, что выходной сигнал, подаваемый на вход в качестве обратной связи, имеет одинаковый знак с входным сигналом. Системы с положительной обратной связью неустойчивы. Свойством адаптивности обладает система, имеющая управление с обратной связью, которая отличается наличием специального адаптивного механизма, накапливающего и анализирующего информацию о прошлых управленческих ситуациях, вырабатывающего новое поведение. Адаптивное управление присуще сложным системам, которым в процессе управления приходится изменять программы и стратегии поведения путем обучения. Теория адаптивного управления пока не получила большого развития, в следствие чрезвычайной сложности формирования процессов обучения. Открытость – означает, что система имеет связь со средой. Закрытость – система не имеет связи со средой. Классификация моделей систем (статические, динамические, концептуальные, топологические, формализованные (процедуры формализации моделей систем), информационные, логико-лингвистические, семантические, теоретико-множественные) 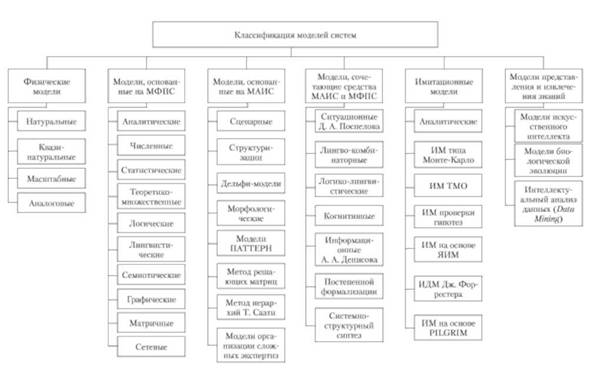 Классификацию систем можно осуществить по разным критериям. Проводить ее жестко - невозможно, она зависит от цели и ресурсов. Приведем основные способы классификации (возможны и другие критерии классификации систем). 1. По отношению системы к окружающей среде: a. открытые (есть обмен ресурсами с окружающей средой); b. закрытые (нет обмена ресурсами с окружающей средой). 2. По происхождению системы (элементов, связей, подсистем): a. искусственные (орудия, механизмы, машины, автоматы, роботы и т.д.); b. естественные (живые, неживые, экологические, социальные и т.д.); c. виртуальные (воображаемые и, хотя реально не существующие, но функционирующие так же, как и в случае, если бы они существовали); d. смешанные (экономические, биотехнические, организационные и т.д.). 3. По описанию переменных системы: a. с качественными переменными (имеющие лишь содержательное описание); b. с количественными переменными (имеющие дискретно или непрерывно описываемые количественным образом переменные); c. смешанного (количественно-качественное) описания. 4. По типу описания закона (законов) функционирования системы: a. типа "Черный ящик" (неизвестен полностью закон функционирования системы; известны только входные и выходные сообщения); b. не параметризованные (закон не описан; описываем с помощью хотя бы неизвестных параметров; известны лишь некоторые априорные свойства закона); c. параметризованные (закон известен с точностью до параметров и его возможно отнести к некоторому классу зависимостей); d. типа "Белый (прозрачный) ящик" (полностью известен закон). 5. По способу управления системой (в системе): a. управляемые извне системы (без обратной связи, регулируемые, управляемые структурно, информационно или функционально); b. управляемые изнутри (самоуправляемые или саморегулируемые - программно управляемые, регулируемые автоматически, адаптируемые - приспосабливаемые с помощью управляемых изменений состояний, и самоорганизующиеся - изменяющие во времени и в пространстве свою структуру наиболее оптимально, упорядочивающие свою структуру под воздействием внутренних и внешних факторов); c. с комбинированным управлением (автоматические, полуавтоматические, автоматизированные, организационные). Задачей системного анализа является определение свойств изучаемой системы. Изучение этих свойств позволяет в последующем выбрать для соответствующей задачи метод построения модели. Таким образом, системный анализ является инструментом, позволяющим изучать функционирование сложных технологических систем и выбирать методы моделирования таких систем. Основные задачи системного анализа: • задача декомпозиции, т.е. разложение системы (проблемы) на отдельные подсистемы (задачи); • задача анализа заключается в определении законов и закономерностей поведения системы посредством обнаружения системных свойств и атрибутов; • задача синтеза сводится к созданию новой модели системы, определению ее структуры и параметров на основе полученных при решении задач знаний и информации. В системном анализе применяются специальные методы моделирования: – имитационное моделирование, на основе методов статистики и языков программирования; – ситуативное моделирование, на основе методов теории множеств, теории алгоритмов, математической логики и представления проблемных ситуаций; – информационное моделирование, на основе математических методов теории информационного поля и информационных цепей. Кроме того, в системном анализе широко используют методы индукционного и редукционного моделирования. Индукционное моделирование осуществляется с целью получения сведений о специфике объекта-системы, ее структуре и элементах, способах их взаимодействия на основе анализа частного и приведения этих сведений к общему описанию. Индуктивный метод моделирования сложных систем используется в том случае, когда невозможно адекватно представить модель внутренней структуры объекта. Это метод позволяет создать обобщенную модель объекта-системы, сохраняя специфику организационных свойств, связей и отношений между элементами, что отличает ее от другой системы. При построении такой модели часто используют методы логики теории вероятностей, т.е. такая модель становится логической или гипотетической. Затем определяются обобщенные параметры структурно-функциональной организации системы и описываются их закономерности, с помощью методов аналитической и математической логики. Редукционное моделирование используют для того, чтобы получить информацию о законах и закономерностях взаимодействия в системе различных элементов с целью сохранить целое структурное образование. Модели и методы принятия решений Модельюназывается представление объекта, схемы или идеи в некоторой форме, отличной от самого оригинала. Причин использования моделей (вместо непосредственного взаимодействия с реальной действительностью или проведения эксперимента) три. Первая из них – это сложность многих реальных ситуаций, в результате которой анализ последних по сложности превышает возможности человека. А с помощью модели ситуация может быть предельно упрощена за счет устранения не относящихся к делу или малозначащих данных. Вторая причина связана с необходимостью анализа такой ситуации, которой пока в реальной действительности нет, но которая будет или не будет создана в будущем в зависимости от результатов этого анализа. Моделирование является единственным способом «увидеть» варианты будущего, определить и оценить их возможные последствия. Третья причина проистекает из невозможности проведения натурных экспериментов, когда они желательны. Эксперимент – это изучение реальной действительности, в которую вводятся дополнительные условия, существенно меняющие ситуацию; после окончания эксперимента данные условия отменяются. Когда провести эксперимент не представляется возможным, на помощь может прийти моделирование. Существуют три базовых типа моделей: 1. Физическая модель представляет то, что исследуется с помощью увеличенного или уменьшенного описания объекта или системы. (например, уменьшенная фактическая модель завода, уменьшенный чертеж). Такая физическая модель упрощает визуальное восприятие и помогает решить фактические проблемы. 2. Аналоговая модель представляет исследуемый объект аналогом, который ведет себя как реальный объект, но не выглядит как таковой (например, график, иллюстрирующий соотношения между объемом производства и издержками, организационная схема предприятия). 3. Математическая модель использует цифровые значения, символы для описания свойств или характеристик объекта или события. Построение модели, как и управление, является процессом. Основные этапы такого процесса: постановка задачи. Построение модели, способной обеспечить правильное решение управленческой проблемы, состоит в верной постановке задачи. построение модели. Разработчик должен определить главную цель модели, какие выходные нормативы или информацию предполагается получить, используя модель и непосредственно создать модель. проверка модели на достоверность. Проверка заключается в определении степени соответствия модели реальному миру. применение модели. Модель нельзя считать успешно выстроенной, пока она не принята, не понята и не применена на практике. Основная причина недоиспользования моделей заключается в том, что руководители опасаются или не понимают, как их применить. обновление модели. Руководство может обнаружить, что форма выходных данных не ясна, желательны дополнительные данные или цели организации изменяются таким образом, что это влияет на критерии принятия решений, следовательно, модель нужно соответствующим образом модифицировать. 3. Модели и методы принятия решений при нечеткой информации. Человек мыслит нечеткими понятиями: погода хорошая, скорость низкая, настроение хорошее. Очевидно, что каждый может вкладывать в эти понятия совершенно разный смысл: что хорошо для одного, может быть совершенно неприемлемо для другого. Четкая логика (в рамка которой переменная может принимать всего два значения: истина и ложь, 0 и1) учет этого фактора совершенно невозможен. Поэтому в середине XX века Л.Заде была предпринята попытка создания математического аппарата, позволяющего учесть эту особенность мыслительной деятельности человека. Лингвистическая переменная (ЛП) – это переменная, значение которой определяется набором вербальных (то есть словесных) характеристик некоторого свойства. Например, ЛП «рост» определяется через набор {карликовый, низкий, средний, высокий, очень высокий}. Введя понятие лингвистической переменной и допустив, что в качестве ее значений (термов) выступают нечеткие множества, был предложен аппарат для описания процессов интеллектуальной деятельности, включая нечеткость и неопределенность выражений. Это позволило создать фундамент теории нечетких множеств и нечеткой логики, а также предпосылки для внедрения методов нечеткого управления в инженерную практику. Основы теории нечетких множеств Значения лингвистической переменной (ЛП) определяются через так называемые нечеткие множества (НМ), которые в свою очередь определены на некотором базовом наборе значений или базовой числовой шкале, имеющей размерность. Каждое значение ЛП определяется как нечеткое множество (например, НМ «низкий рост»). Нечеткое множество определяется через некоторую базовую шкалу В и функцию принадлежности НМ – µ(х), х 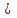 В, принимающую значения на интервале [0...1]. Таким образом, нечеткое множество В – это совокупность пар вида (х, µ(х)), где х В, принимающую значения на интервале [0...1]. Таким образом, нечеткое множество В – это совокупность пар вида (х, µ(х)), где х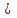 В. Часто встречается и такая запись: В. Часто встречается и такая запись: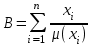 (6.1) (6.1)где х – i-e значение базовой шкалы. Функция принадлежности определяет субъективную степень уверенности эксперта в том, что данное конкретное значение базовой шкалы соответствует определяемому НМ. Эту функцию не стоит путать с вероятностью, носящей объективный характер и подчиняющейся другим математическим зависимостям. Например, для двух экспертов определение НМ «высокая» для ЛП «цена автомобиля» в условных единицах может существенно отличаться в зависимости от их социального и финансового положения. «Высокая_цена_автомобиля_1» = {50000/1 + 25000/0.8 + 10000/0.6 + 5000/0.4}; «Высокая_цена_автомобиля_2» = {25000/1 + 10000/0.8 + 5000/0.7 + 3000/0.4}. Пример.6.1 Пусть перед нами стоит задача интерпретации значений ЛП «возраст», таких как «молодой» возраст, «преклонный» возраст или «переходный» возраст. Определим «возраст» как ЛП (рис.6.1.). Тогда «молодой», «преклонный», «переходный» будут значениями этой лингвистической переменной. Более полно базовый набор значений ЛП «возраст» следующий: В – {младенческий, детский, юный, молодой, зрелый, преклонный, старческий}. Для ЛП «возраст» базовая шкала – это числовая шкала от 0 до 120, обозначающая количество прожитых лет, а функция принадлежности определяет, насколько мы уверены в том, что данное количество лет можно отнести к данной категории возраста (от 0 до 1). На рис.6.2 отражено, как одни и те же значения базовой шкалы могут участвовать в определении различных НМ. 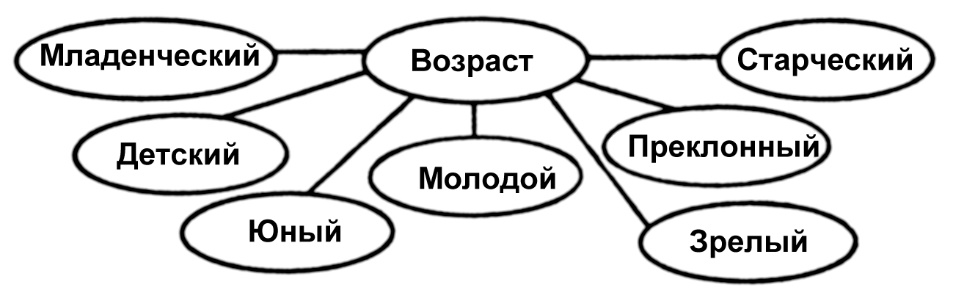 Рис. 6.1. Лингвистическая переменная «возраст» и нечеткие множества, определяющие ее значения Например, определить значение НМ «младенческий возраст» можно так: 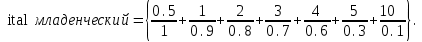 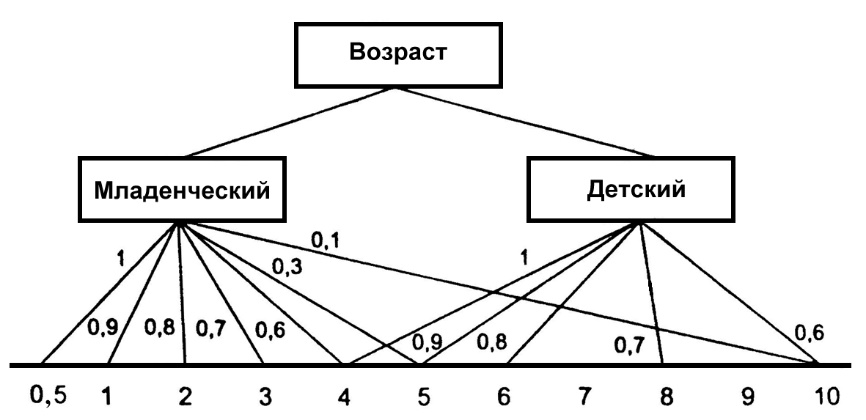 Рис. 6.2. Формирование нечетких множеств Рис.6.3 иллюстрирует оценку НМ неким усредненным экспертом, который ребенка до полугода с высокой степенью уверенности относит к младенцам (m=1). Дети до четырех лет причисляются к младенцам тоже, но с меньшей степенью уверенности (0.5 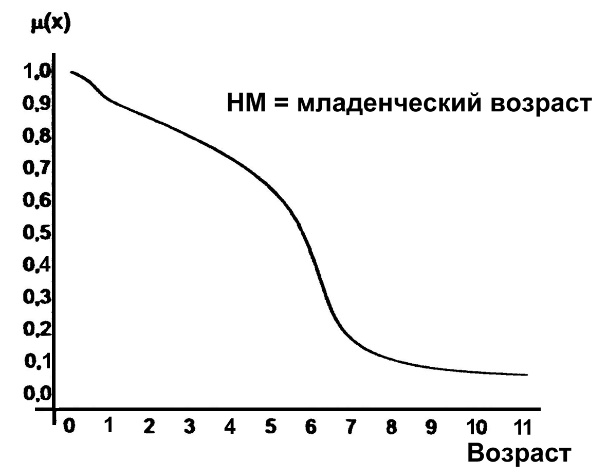 Рис. 6.3. График функции принадлежности нечеткому множеству «младенческий возраст». Основные характеристики нечетких множеств Пусть М = [0,1] и A – нечеткое множество с элементами из универсального множества Е и множеством принадлежностей М. Величина 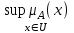 называется высотой нечеткого множества А. Нечеткое множество А нормально, если его высота равна 1, т.е. верхняя граница его функции принадлежности равна называется высотой нечеткого множества А. Нечеткое множество А нормально, если его высота равна 1, т.е. верхняя граница его функции принадлежности равна 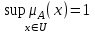 . При . При 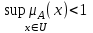 нечеткое множество называется субнормальным. нечеткое множество называется субнормальным.Нечеткое множество пусто, если 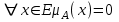 . Непустое субнормальное множество можно нормализовать по формуле: . Непустое субнормальное множество можно нормализовать по формуле: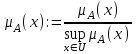 . .Нечеткое множество унимодально, если µА(х) = 1 только на одном х из Е. Носителем нечеткого множества А является обычное подмножество со свойством µА(х)>0, т.е. носитель 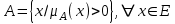 . .Элементы х 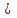 Е, для которых µА(х) = 0.5, называются точками перехода множества А. Е, для которых µА(х) = 0.5, называются точками перехода множества А.Нечеткие числа – нечеткие переменные, определенные на числовой оси, т.е. нечеткое число определяется как нечеткое множество А на множестве действительных чисел R с функцией принадлежности 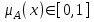 , где , где 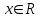 . .Нечеткое число А нормально, если 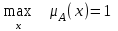 , и выпуклое, если для любых , и выпуклое, если для любых 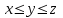 выполняется выполняется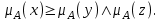 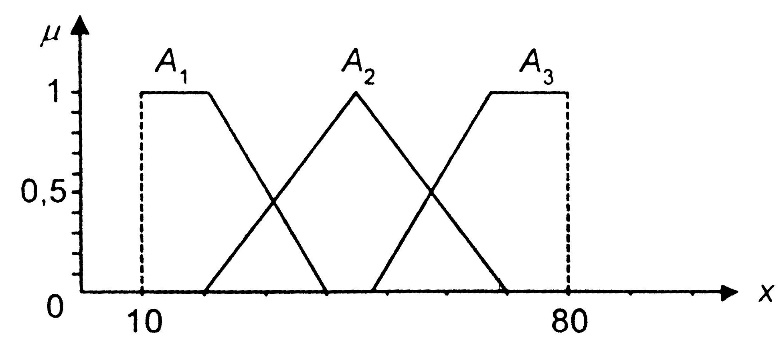 Рис. 6.4. Функции принадлежности нечетких множеств: А1 – «малая толщина»; А2 – «средняя толщина»; А3 – «большая толщина» Нечеткие правила вывода Базовое правило вывода типа "если - то" (англ.: if- then rule)называется также нечеткойимпликацией, принимающей форму если х это А, то у это В (6.1) где А и В - это лингвистические значения, идентифицированные нечетким способом через соответствующие функции принадлежности для переменных х и у. Часть "х это А" называется условием (предпосылкой),а "у это В" - следствием (заключением). Импликацию (6.1) можно записать в сокращенном виде А → В. Нечеткое рассуждение - это процедура, которая позволяет определить заключение, вытекающее из множества правил "если - то". Такое множество при N переменных х может принять вид если x1это А1 и х2 это А2 и ... и xN это AN, тo у это В (6.2) Переменные x1, x2, …,xNобразуют N-мерный входной вектор x, составляющий аргумент условия, в котором А1, А2 , ..., Anи В обозначают величины соответствующего коэффициента принадлежности интерпретация в форме логического произведения (из всех нечетких значений переменных условия правила берется минимальное): интерпретация в форме алгебраического произведения (в качестве нечеткого значения переменной следствия правила берется значение, полученное путем перемножения нечетких значений переменных условия правила): Приписывание единственного значения функции принадлежности, описывающей многомерное условие, будем называть агрегированием предпосылки. Каждой импликации А → В, определенной выражением (6.2), можно приписать также единственное значение функции принадлежности форма логического произведения форма алгебраического произведения Приписывание единственного значения функции принадлежности всей импликации будем называть процедурой агрегирования на уровне импликации. Нечеткий логический вывод Системы нечеткого вывода Мамдани-Заде Элементы теории нечетких множеств, правила импликации и нечетких рассуждений образуют систему нечеткого вывода. В ней можно выделить множество используемых в системе нечетких правил, базу данных, содержащую описания функций принадлежности, а также механизм вывода и агрегирования, который формируется применяемыми правилами импликации. Следует упомянуть, что в случае технической реализации в качестве входных и выходных сигналов выступают измеряемые величины, однозначно сопоставляющие входным значениям соответствующие выходные значения. Для обеспечения взаимодействия множеств этих двух видов вводится нечеткая система с так называемыми фазификатором (преобразователем множества входных данных в нечеткое множество) на входе и дефазификатором (преобразователем нечетких множеств в конкретное значение выходной переменной) на выходе. Структура такой системы представлена на рис.6.5. 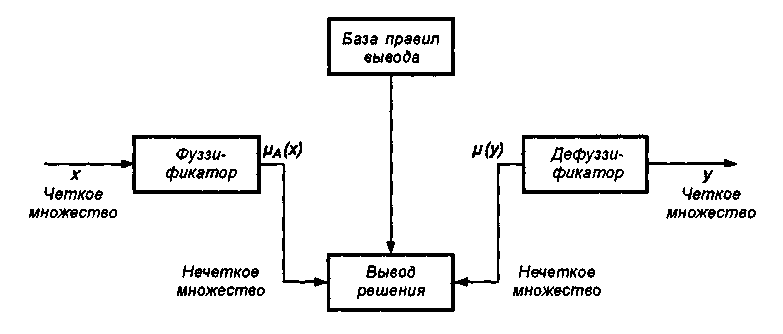 Рис. 6.5. Структура нечеткой системы с фазификатором и дефазификатором Используемый в различного рода экспертных и управляющих системах механизм нечетких выводов в своей основе имеет базу знаний, формируемую специалистами предметной области в виде совокупности нечетких предикатных правил вида: П1: если х есть A1, то у есть В1 П2: если х есть А2, то у есть В2 …………………… Пn: если х есть Аn, то у есть Вn , где х – входная переменная (имя для известных значений данных); у – переменная вывода (имя для значения данных, которое будет вычислено); А и В – функции принадлежности, определенные соответственно на х и у. Приведем более детальное пояснение Знание эксперта A → В отражает нечеткое причинное отношение предпосылки и заключения, поэтому его можно назвать нечетким отношением и обозначить через R: R = A → В, где «→» называют нечеткой импликацией. Отношение R можно рассматривать как нечеткое подмножество прямого произведения X × Y полного множества предпосылок X и заключений Y. Таким образом, процесс получения (нечеткого) результата вывода B' с использованием данного наблюдения А' и знания А→В можно представить в виде композиционного правила нечеткий «modus ponens»: В' = А' • R = А' • (А → В), где «•» – операция свертки. Как операцию композиции, так и операцию импликации в алгебре нечетких множеств можно реализовывать по-разному (при этом будет отличаться и получаемый результат), но в любом случае общий логический вывод осуществляется за следующие пять этапов. 1) Введение нечеткости (фаззификация, fuzzification). Функции принадлежности, определенные на входных переменных, применяются к их фактическим значениям для определения степени истинности каждой предпосылки каждого правила. Четким значениям входных переменных ставятся в соответствие нечеткие значения с помощью функций принадлежности конкретной переменной. 2) Агрегирование. Вычисленное значение истинности для предпосылок каждого правила применяется к заключениям каждого правила. Это приводит к одному нечеткому подмножеству, которое будет назначено каждой переменной вывода для каждого правила. 3) Активизация. В качестве правил логического вывода обычно используются только операции min (МИНИМУМ) или prod (УМНОЖЕНИЕ). В логическом выводе МИНИМУМА функция принадлежности вывода «отсекается» по высоте, соответствующей вычисленной степени истинности предпосылки правила (нечеткая логика «И», то есть для правила берется минимальное значение степени истинности предпосылок). В логическом выводе УМНОЖЕНИЯ функция принадлежности вывода масштабируется при помощи вычисленной степени истинности предпосылки правила. 4) Аккумуляция. Все нечеткие подмножества, назначенные к каждой переменной вывода (во всех правилах), объединяются вместе, чтобы сформировать одно нечеткое подмножество для всех переменных вывода. При подобном объединении обычно используются операции max (МАКСИМУМ) или sum (СУММА) При композиции МАКСИМУМА комбинированный вывод нечеткого подмножества конструируется как поточечный максимум по всем нечетким подмножествам (нечеткая логика «ИЛИ»). При композиции СУММЫ комбинированный вывод нечеткого подмножества формируется как поточечная сума по всем нечетким подмножествам, назначенным переменной вывода правилами логического вывода. 5) Приведение к четкости (дефаззификация, defuzzification) используется, если требуется преобразовать нечеткий набор выводов в четкое число. Существует большее количество методов приведения к четкости, некоторые из которых рассмотрены ниже. Фазификатор Рассмотрим подробнее первый этап процедуры нечеткого вывода. Фазификатор преобразует N-мерный входной вектор х = [ x1, x2, …,xN]в нечеткое множество А, характеризуемое функцией принадлежности 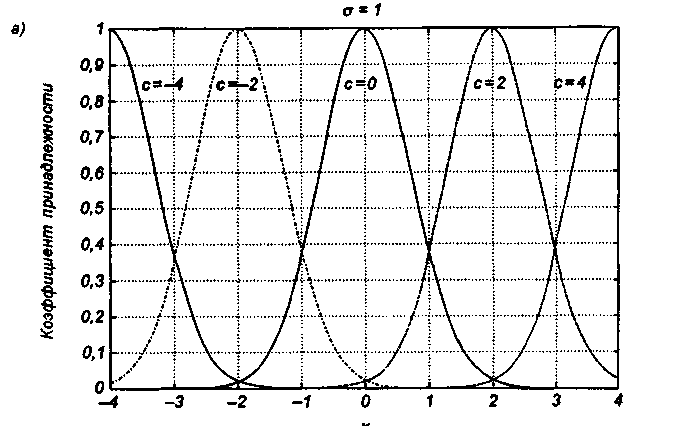 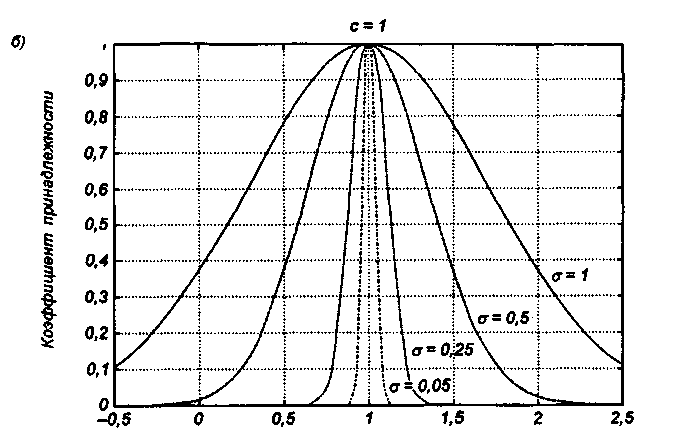 Рис. 6.5 Иллюстрация влияния параметров гауссовской функции на ее форму: а) влияние размещения центра с при σ = 1; б) влияние значения σ при постоянном значении с = 1 Общая форма гауссовой функции для переменной х с центром с и вариацией σдля множества Fимеет вид: 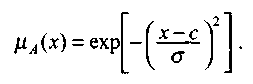 (6.7) (6.7)На рис. 6.5. представлена форма типовых гауссовских функций при различных параметрах с иσ , причем на рис. 6.5а показано влияние размещения центра с при неизменном значении σ, а на рис. 6.5б - влияние значения σ при фиксированном положении с. Параметр с обозначает центр нечеткого множества, а его изменение соответствует смещению функции принадлежности по горизонтальной оси. Праметр σ, иногда называемый коэффициентом широты, отвечает за форму функции. Чем меньше его значение, тем больше крутизна функции. Следует отметить, что при соответствующем смещении центра гауссовская функция может реализовать и сигмоидальную функцию (чаще всего при смещении вправо с с =4). Помимо гауссовской функции принадлежности, на практике часто применяется симметричная треугольная функция, которую можно записать в виде 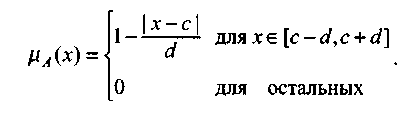 (6.8) (6.8)Интерпретация центральной точки с и ширины dдля треугольной функции представлена на рис.6.6. 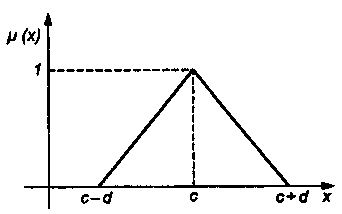 Рис. 6.6 Треугольная форма функции Эта функция тоже нормирована и принимает единичное значение в центральной точке с. Обобщением треугольной функции является трапецеидальная функция принадлежности, форма и обозначения которой показаны на рис. 6.7. 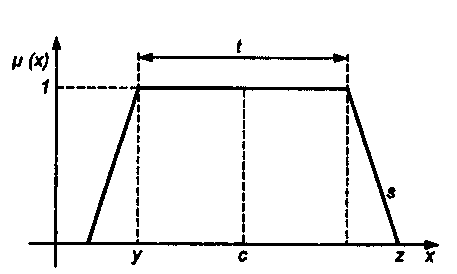 Рис. 6.7 Трапецеидальная форма функции принадлежности Если определить, 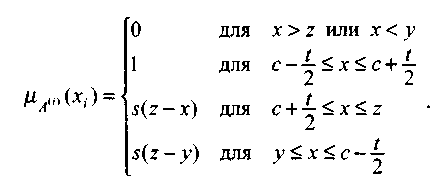 (6.9) (6.9)Выбор значения t= 0 редуцирует трапецеидальную функцию до треугольной формы. Дефазификатор Рассмотрим подробнее последний этап процедуры нечеткого вывода. Дефазификатор трансформирует нечеткое множество в полностью детерминированное точечное решение у. Нечеткое множество представляет зависимость 1) центроидный. В общем случае: 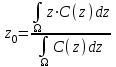 ; (6.10) ; (6.10)для дискретного варианта: 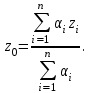 (6.11) (6.11)Первый максимум (First-of-Maxima). Четкая величина вывода находится как наименьшее значение, при котором достигается максимум итогового нечеткого множества (рис. 6.8, a). Средний максимум (Middle-of-Maxima). Четкое значение находится по формуле: 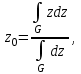 (6.12) (6.12)где G − подмножество элементов, максимизирующих С (рис.6.8,б). Для дискретного варианта (С дискретно): 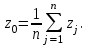 (6.13) (6.13)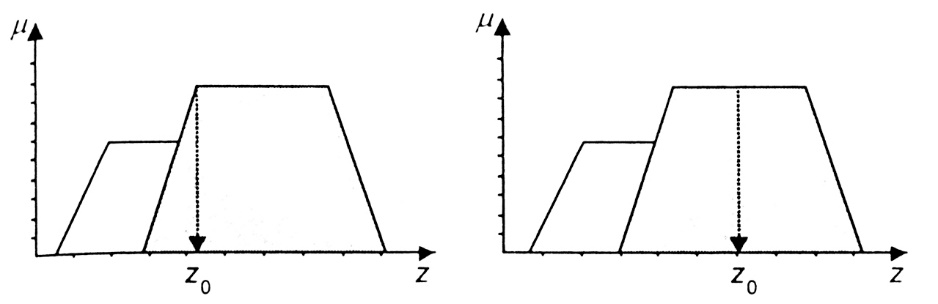 Рис. 6.8. Иллюстрация к методам приведения к четкости: а - первый максимум; б - средний максимум 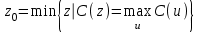 (6.14) (6.14)4) Критерий максимума (Max-Criterion). Четкое значение выбирается произвольно среди множества элементов, для которых С достигает максимума: 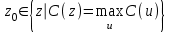 (6.15) (6.15)5) Высотная дефаззификация (Height defuzzification). Элементы области определения Ω, для которых значения функции принадлежности меньше, чем некоторый уровень α, в расчет не принимаются, и четкое значение рассчитывается в соответствии с выражением: 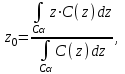 (6.16) (6.16)где Сα – нечеткое множество α-уровня (см. выше). Операции над нечеткими отношениями Объединение двух отношений R1 и R2. Объединение двух отношений обозначается R1 ∪ R2 и определяется выражением Пересечение двух отношений. Пересечение двух отношений R1 и R2 обозначается R1 ⋂ R2 и определяется выражением Алгебраическое произведение двух отношений. Алгебраическое произведение двух отношений R1 и R2 обозначается R1· R2 и определяется выражением Алгебраическая сумма двух отношений. Алгебраическая сумма двух отношений R1 и R2 обозначается Для введенных операций справедливы следующие свойства дистрибутивности: 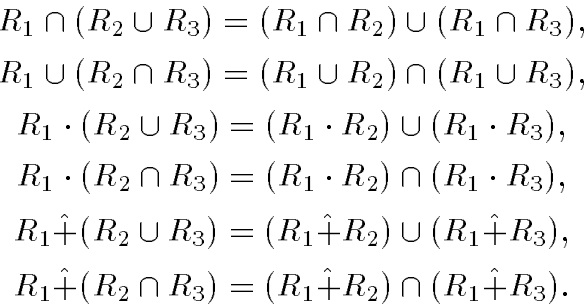 Дополнение отношения. Дополнение отношения R обозначается ̅R и определяется функцией принадлежности: Дизъюнктивная сумма двух отношений. Дизъюнктивная сумма двух отношений R1 и R2 обозначается R1⊕ R2 и определяется выражением Обычное отношение, ближайшее к нечеткому. Пусть R — нечеткое отношение с функцией принадлежности μR(x, у).Обычное отношение, ближайшее к нечеткому, обозначается Rи определяется выражением  По договоренности принимают μR(x, у)= 0 при μR(x, у)= 0,5. Композиция (свертка) двух нечетких отношений. Пусть R1 — нечеткое отношение R1:(X × У) → [0, 1] между X и Y, и R2 — нечеткое отношение R2 — (Y× Z) → [0, 1] между Y и Z. Нечеткое отношение между X и Z, обозначаемое R2 ᵒ R1, определенное через R2 и R1 выражением 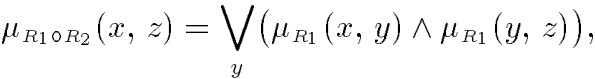 называется (max-min)-композицией ((max-min)-сверткой) отношений R1 и R2 |
