§5. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Определение. Скалярным произведением двух векторов  и и 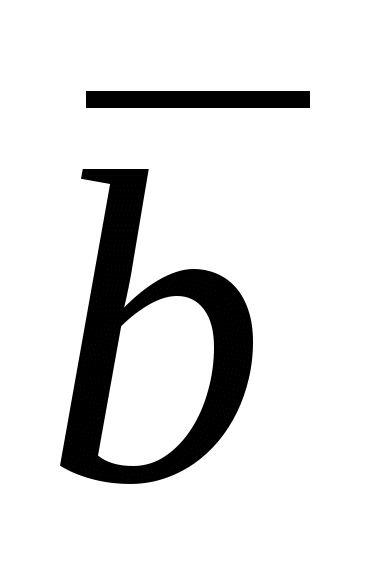 называется число, равное произведению называется число, равное произведению 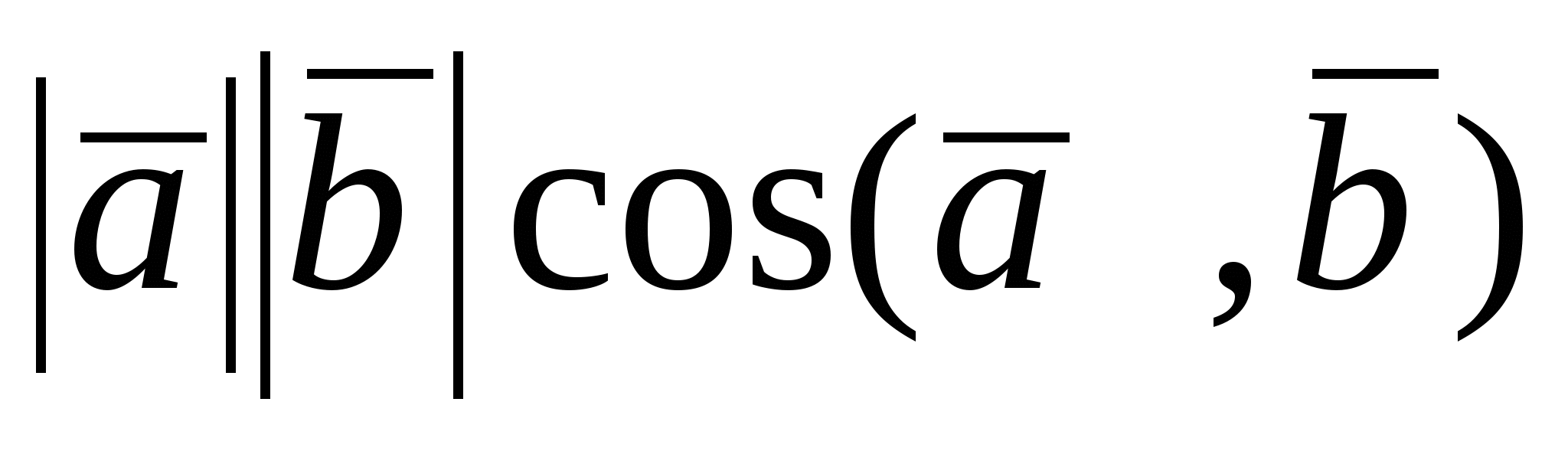 . Обозначается скалярное произведение векторов . Обозначается скалярное произведение векторов  и и 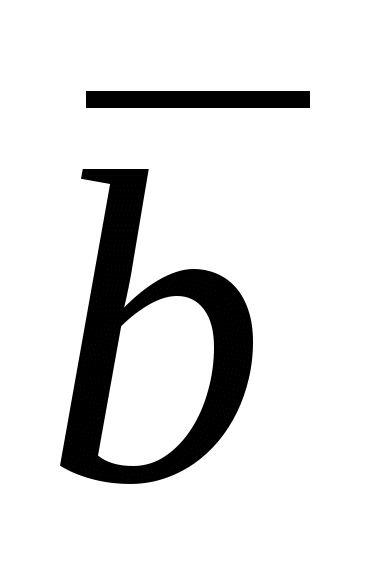 символом символом 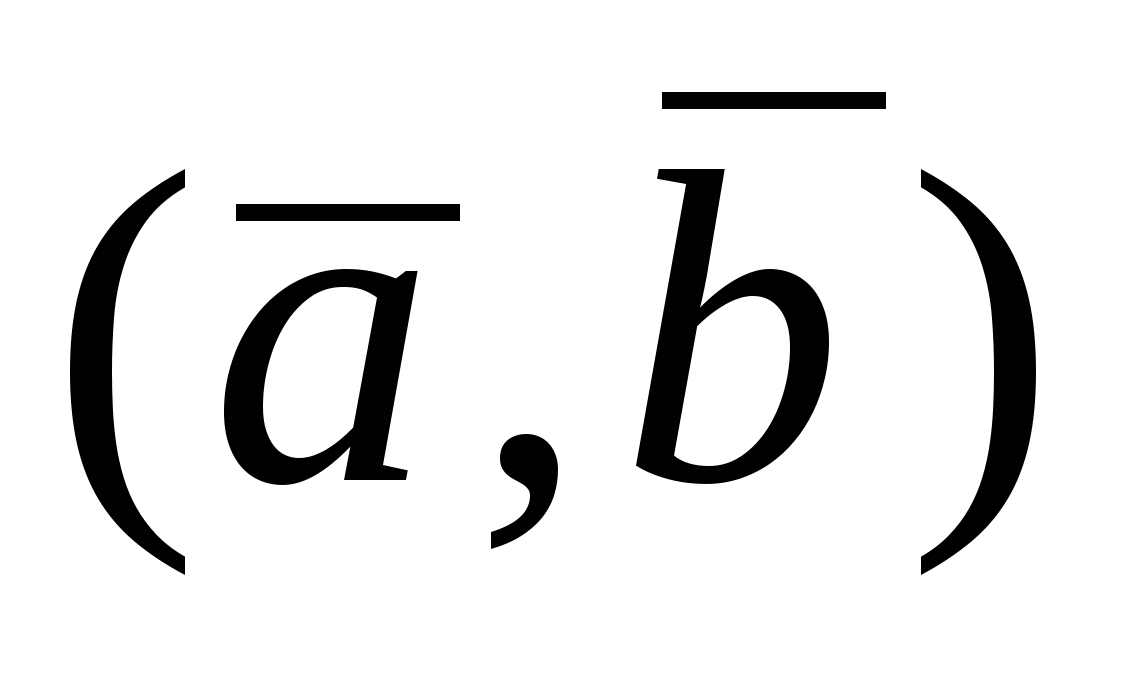 или или 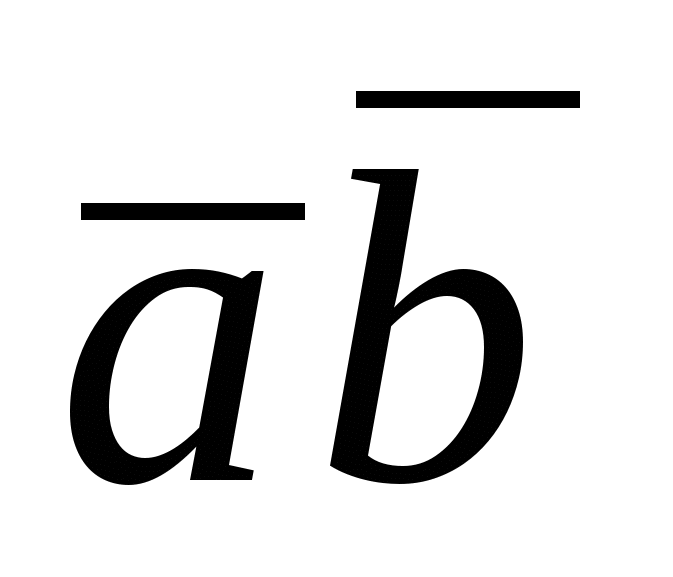 , следовательно, , следовательно, 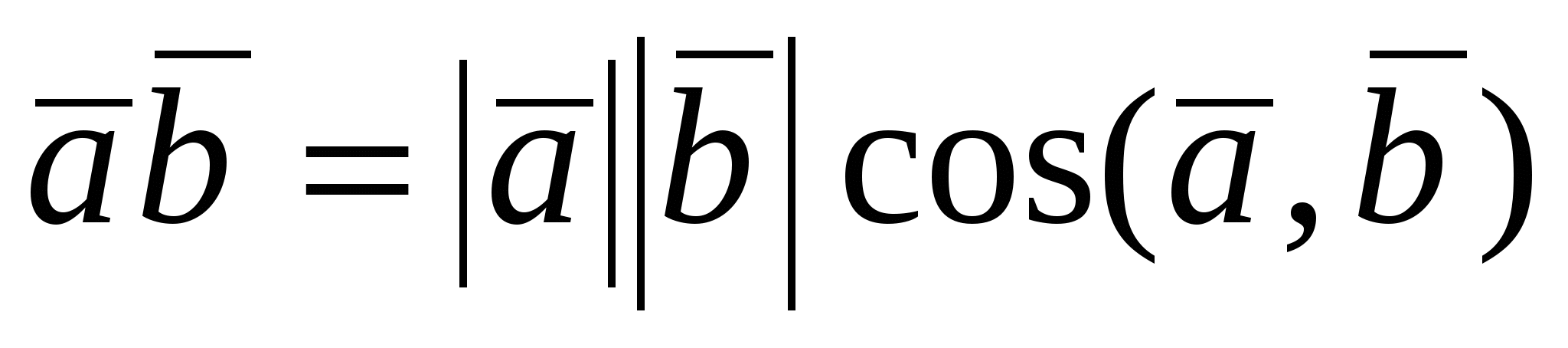 . .
Из определения скалярного произведения следует, что 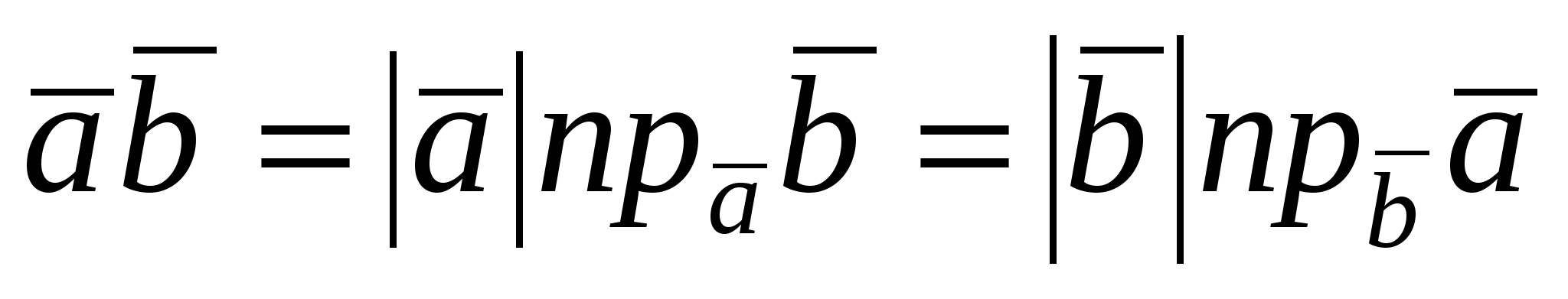 , так как , так как 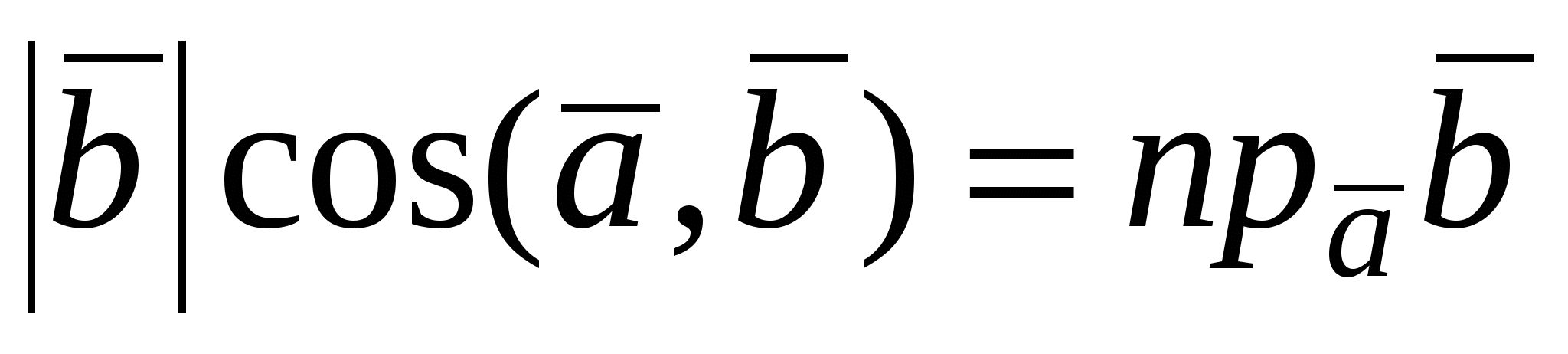 и и 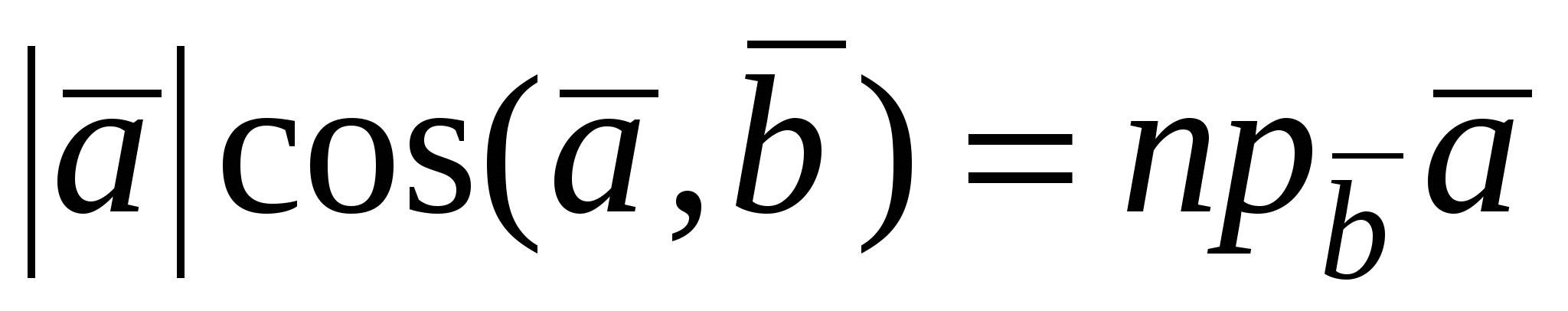 / /
Если один из сомножителей скалярного произведения, например, вектор  есть единичный вектор, то есть единичный вектор, то 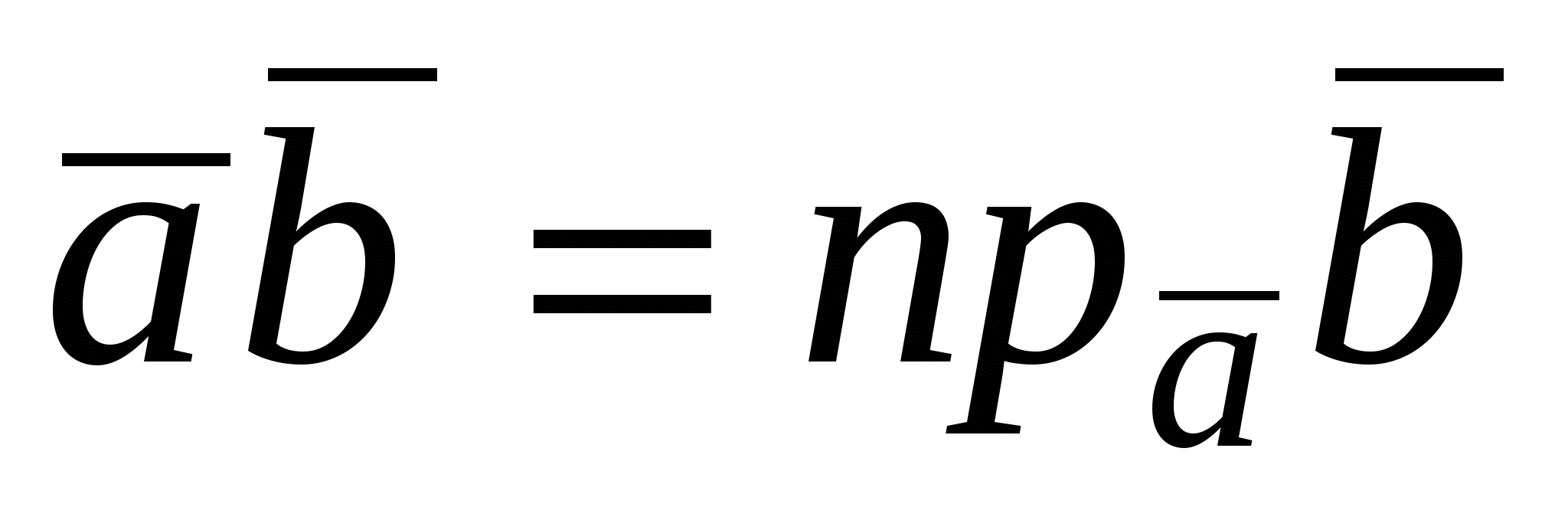 . .
СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ
1. 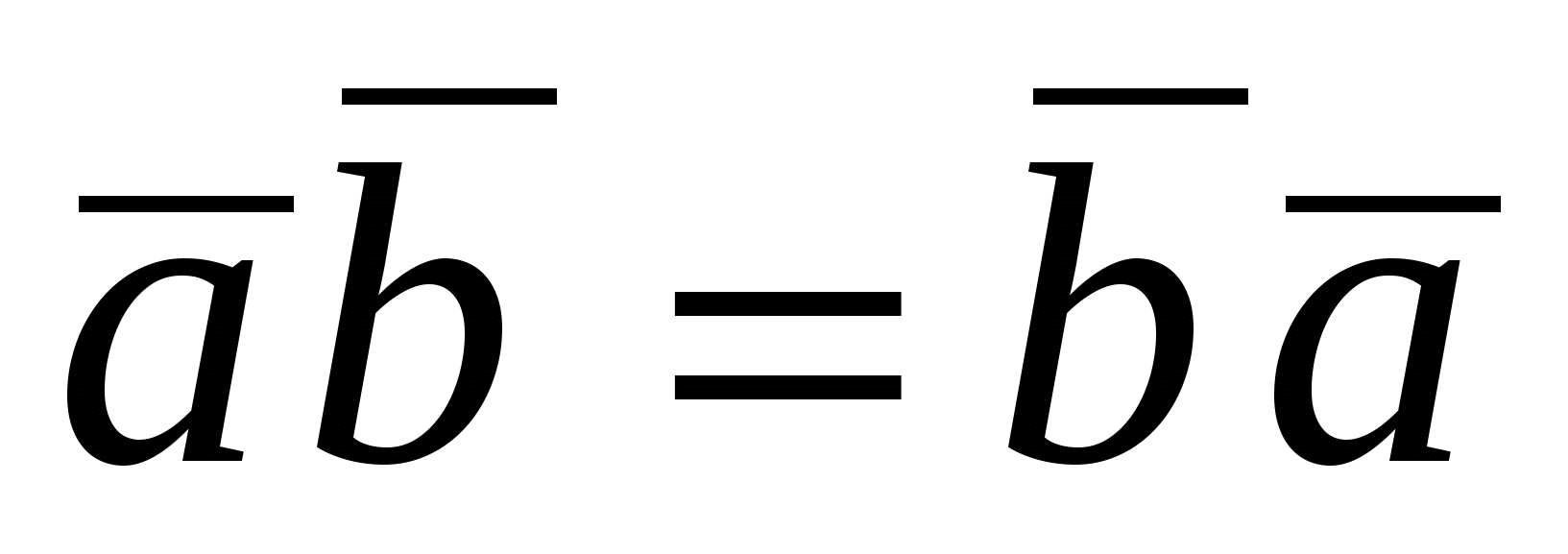 , (коммутативность); , (коммутативность);
2. 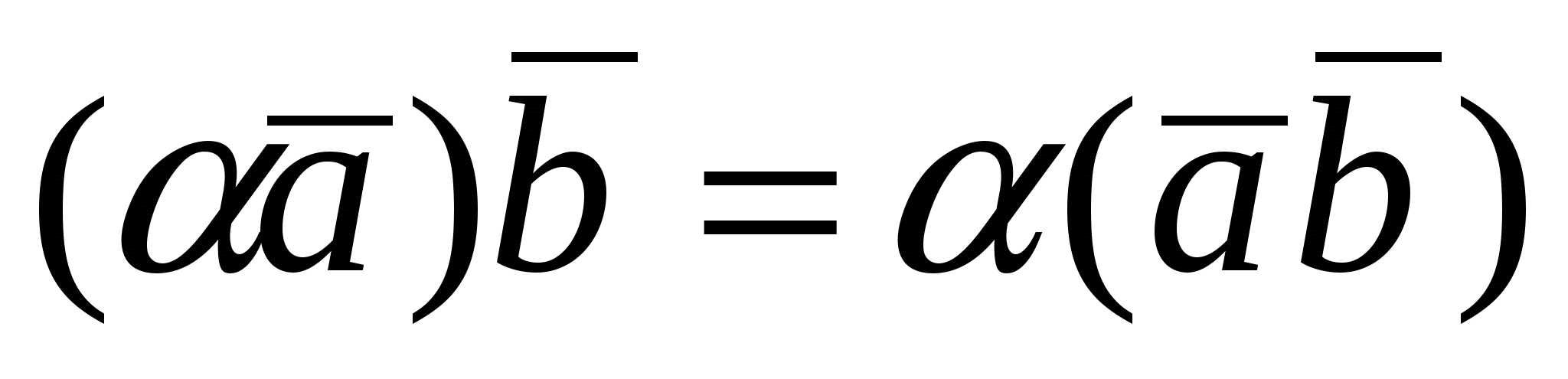 , (ассоциативность относительно числового множителя); , (ассоциативность относительно числового множителя);
3. 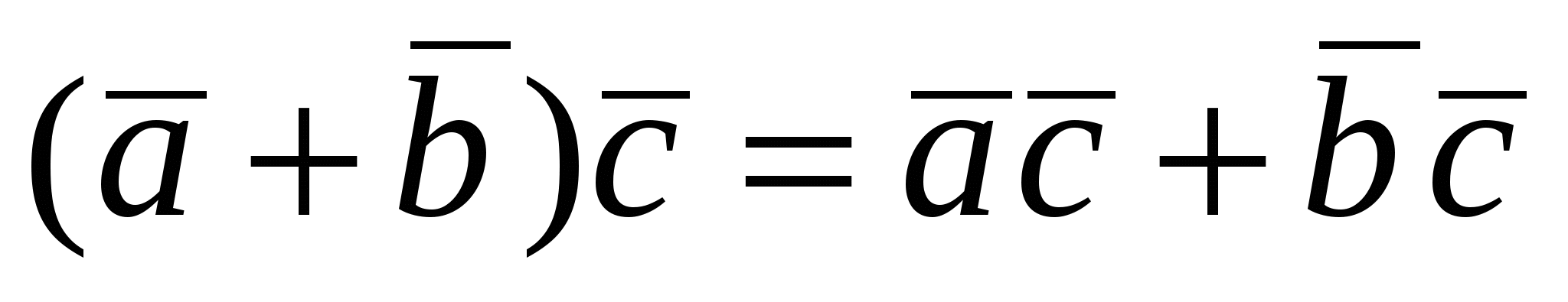 , (дистрибутивность). , (дистрибутивность).
ДОКАЗАТЕЛЬСТВО СВОЙСТВ СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ
Свойство первое следует из определения скалярного произведения: 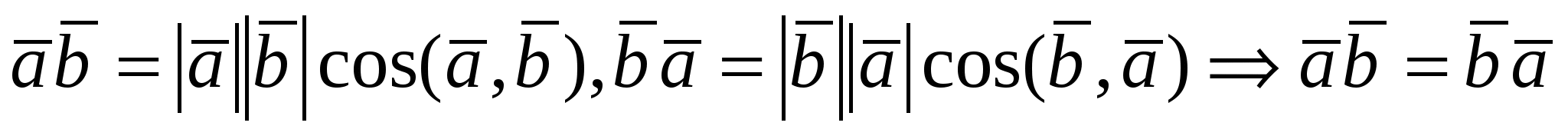 . .
Второе и третье свойства следуют из линейных свойств проекции вектора на ось (направление): 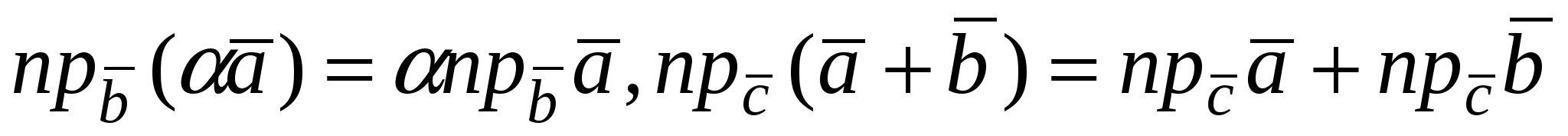 (эти свойства проекции доказываются при рассмотрении вектора в ортонормированном базисе). Используя линейные свойства проекции, получим: (эти свойства проекции доказываются при рассмотрении вектора в ортонормированном базисе). Используя линейные свойства проекции, получим: 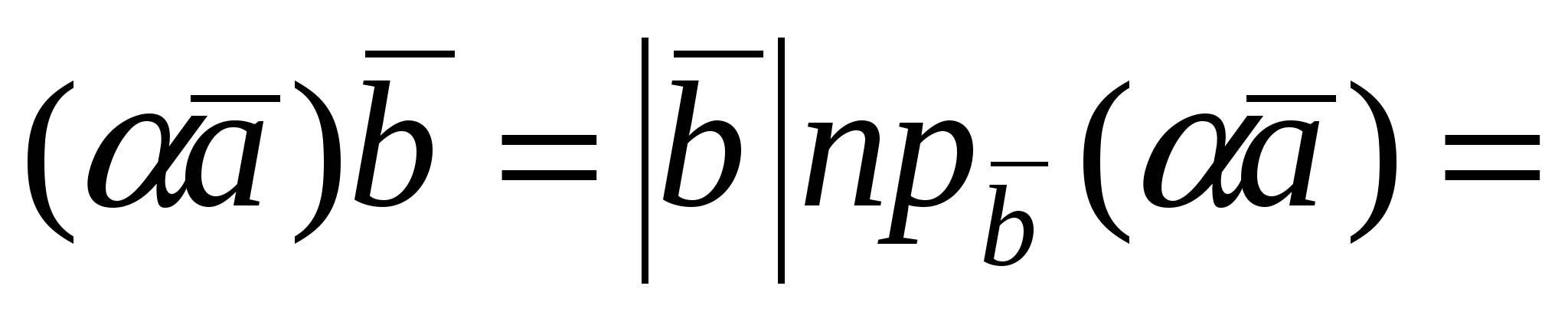 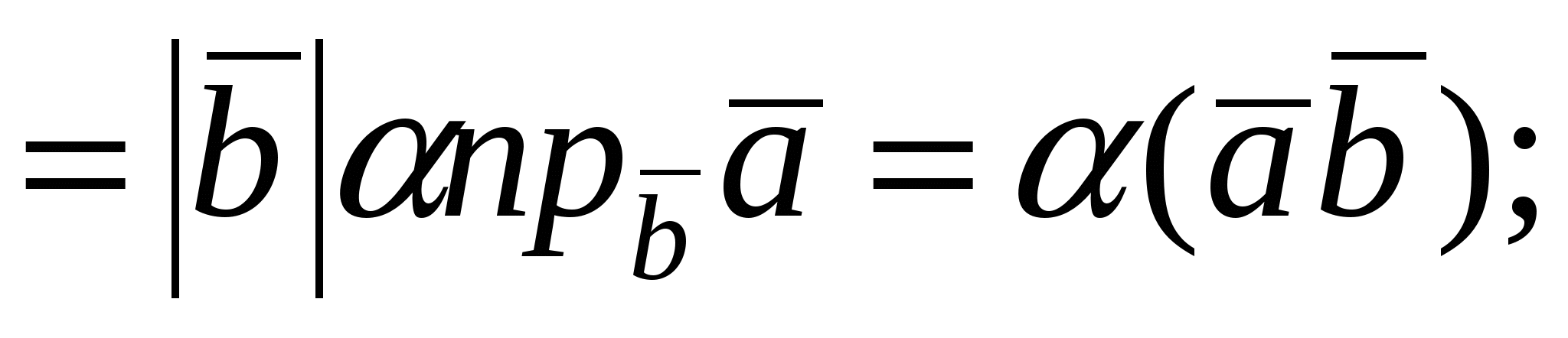 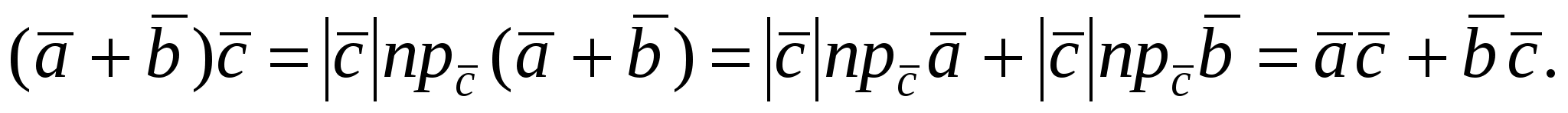
СКАЛЯРНЫЙ КВАДРАТ
Скалярным квадратом называется скалярное произведение 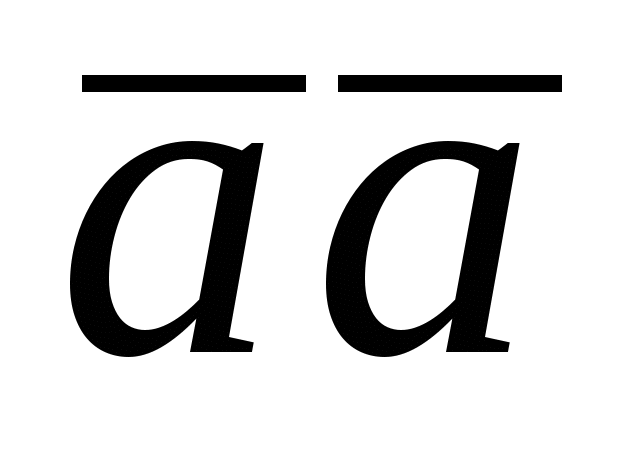 и обозначается символом и обозначается символом 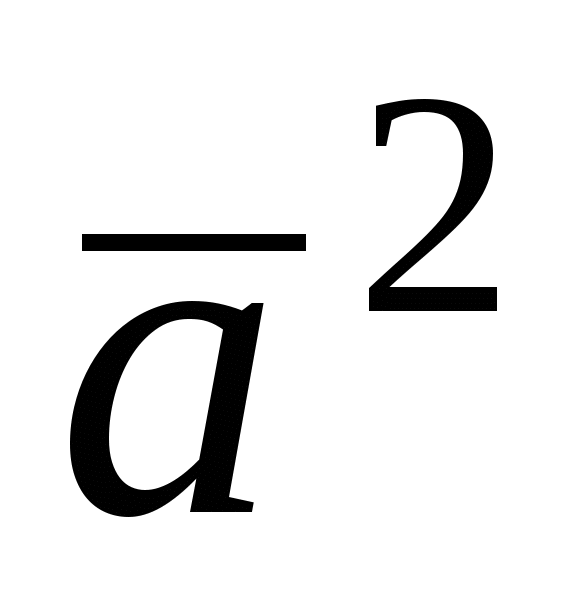 ; по определению ; по определению 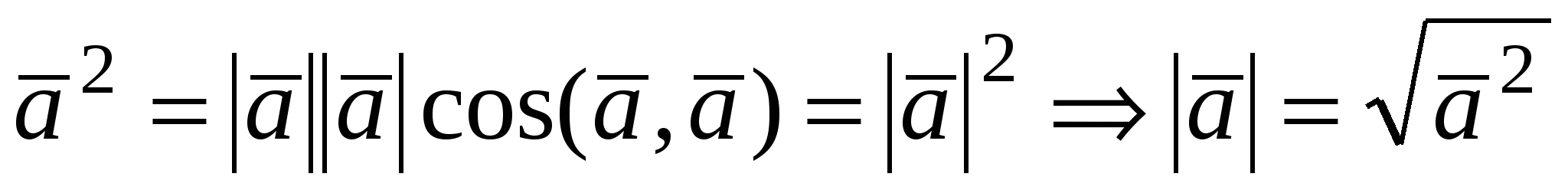 . .
УГОЛ МЕЖДУ ВЕКТОРАМИ
Из определения 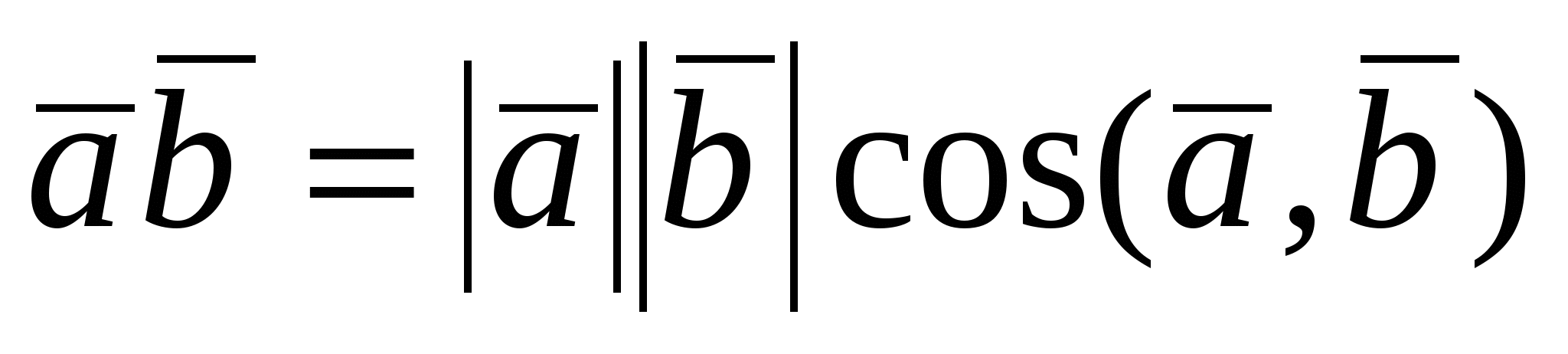 следует следует 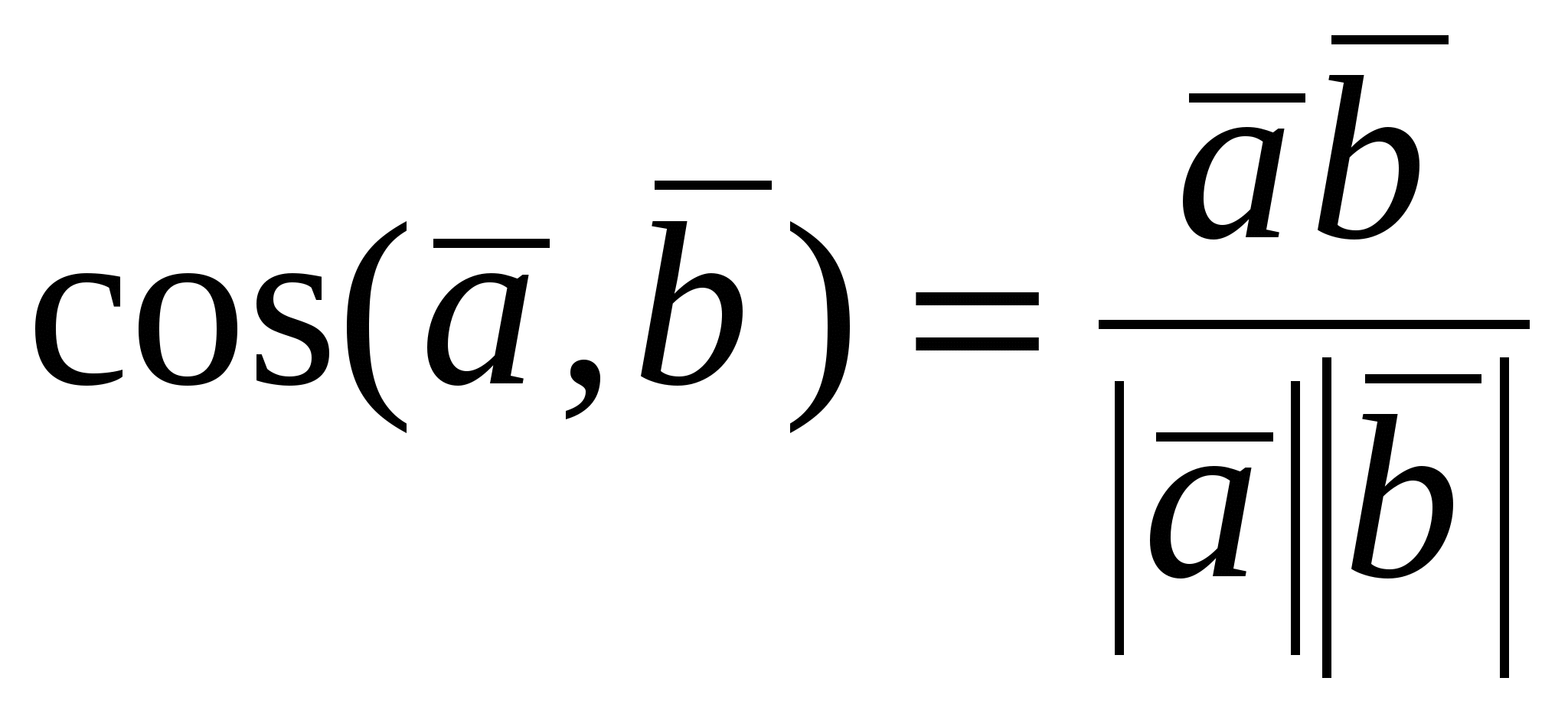 . .
УСЛОВИЕ ОРТОГОНАЛЬНОСТИ ДВУХ ВЕКТОРОВ
Теорема. Векторы  и и 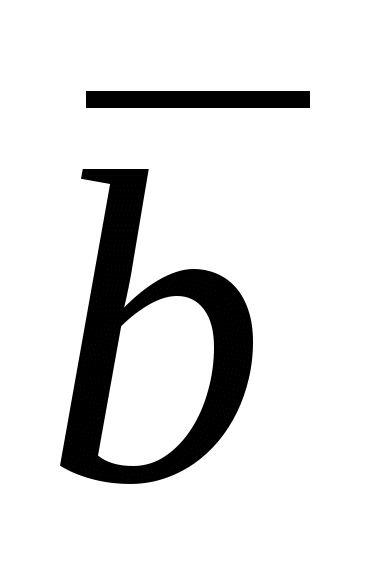 ортогональны тогда и только тогда, когда ортогональны тогда и только тогда, когда 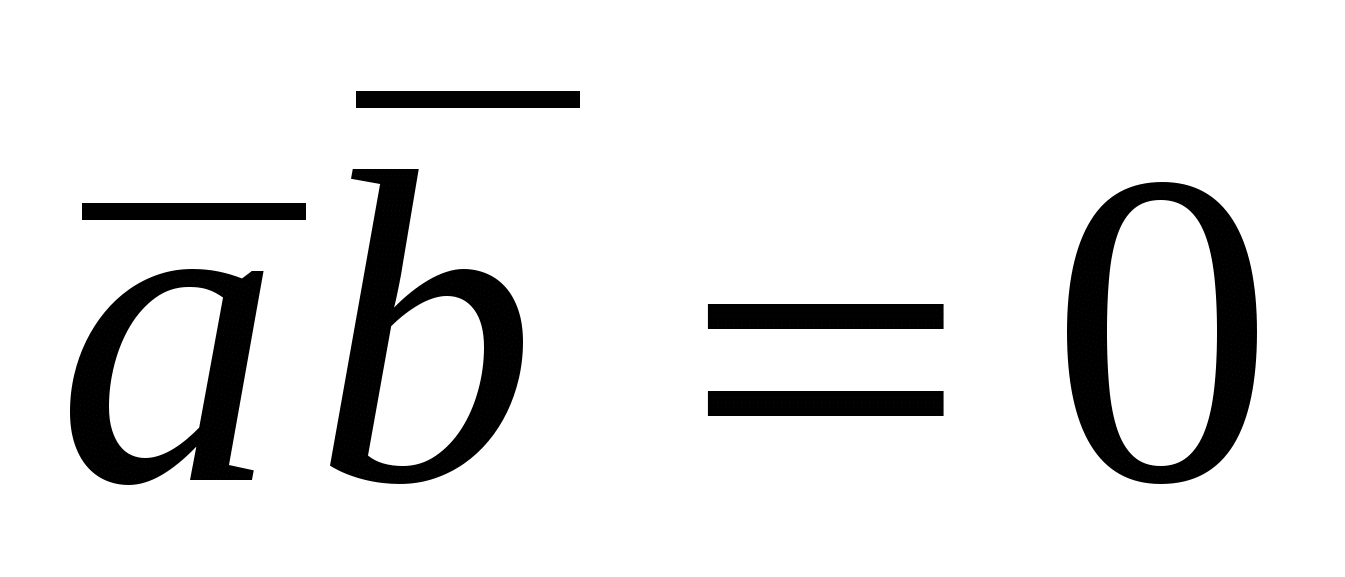 . .
Доказательство необходимости. Пусть 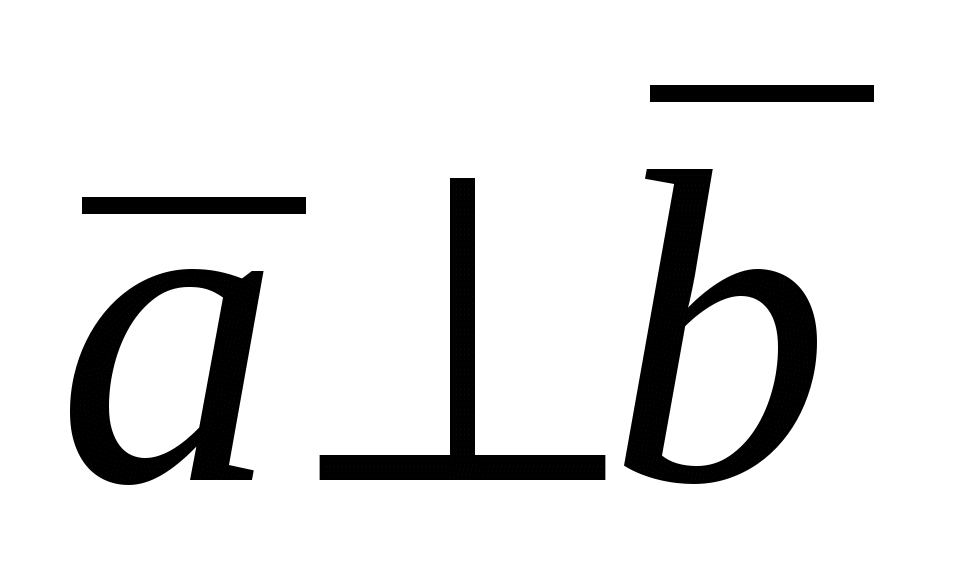 , тогда , тогда 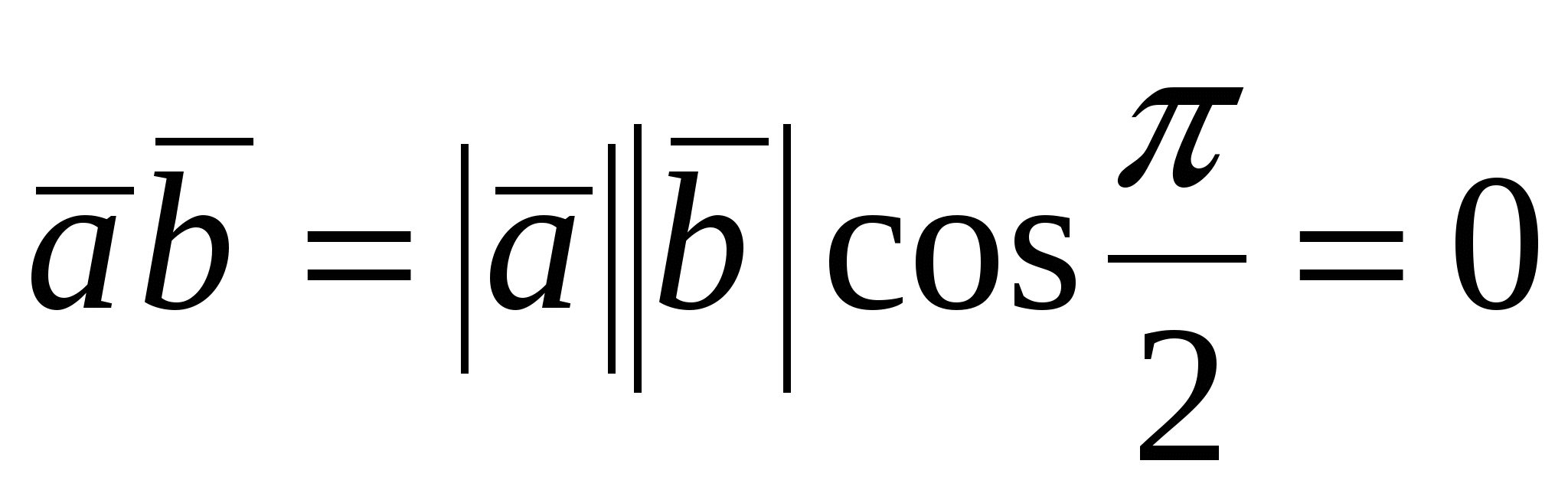  . .
Доказательство достаточности. Пусть  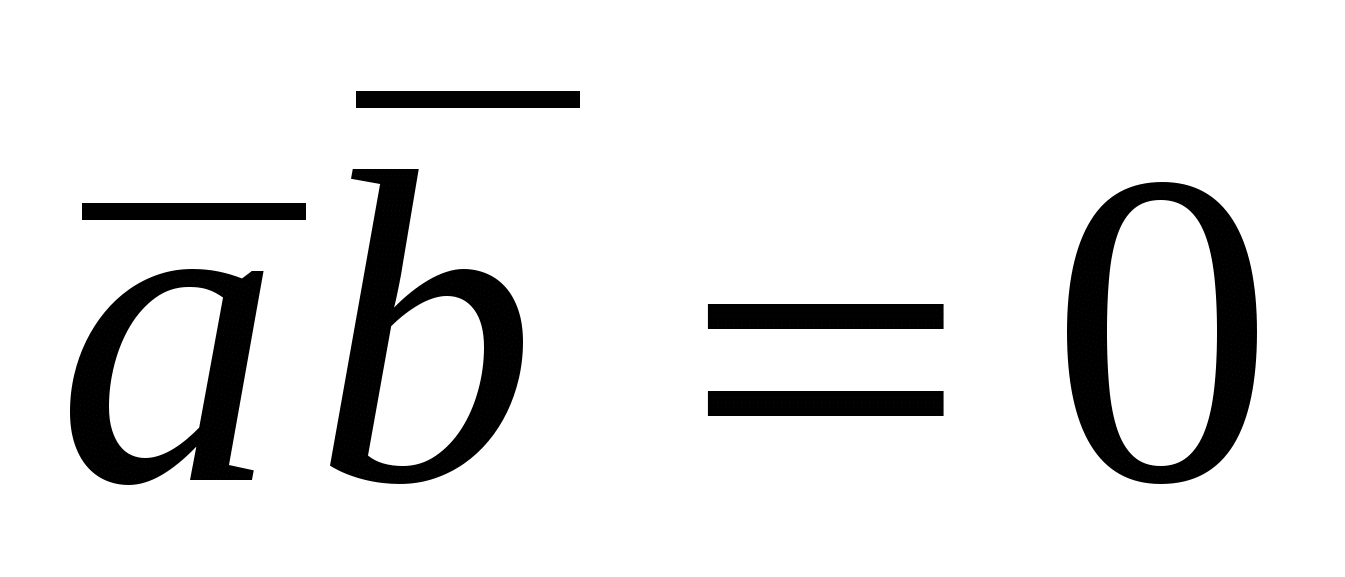 или или 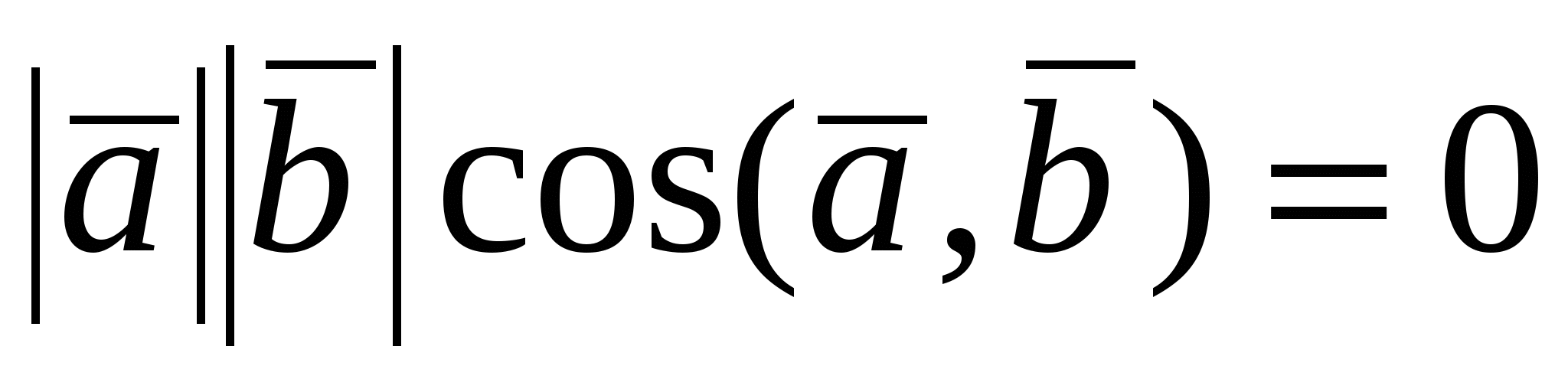 , тогда, либо хотя бы один из множителей есть нулевой вектор и , тогда, либо хотя бы один из множителей есть нулевой вектор и 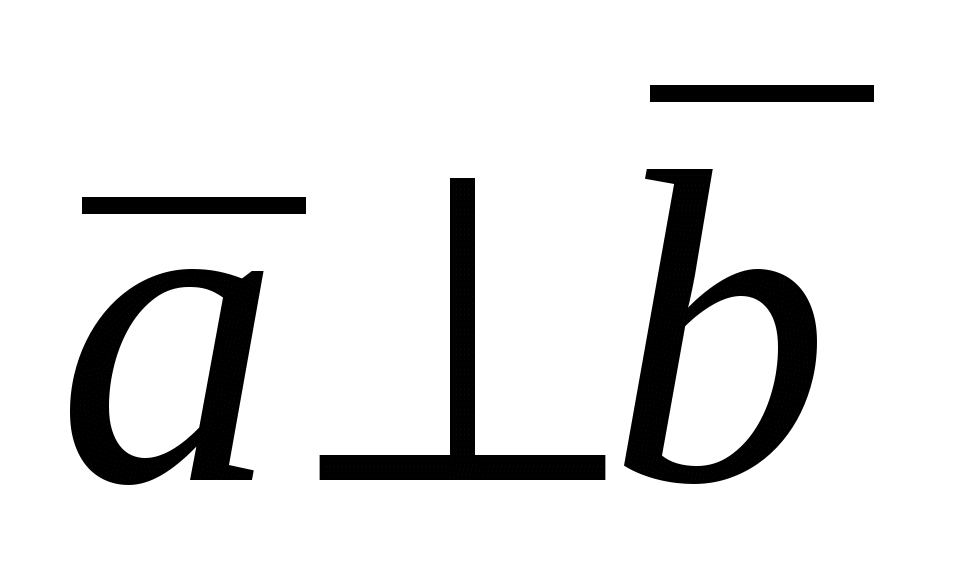 , так как направление нулевого вектора неопределенно, либо , так как направление нулевого вектора неопределенно, либо 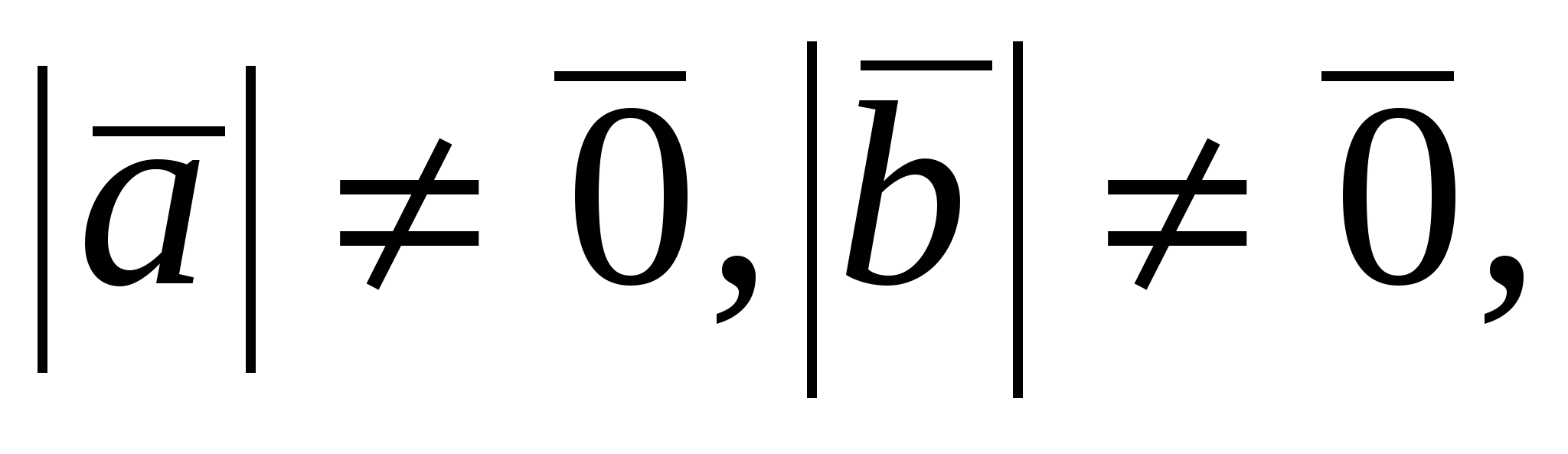 тогда тогда 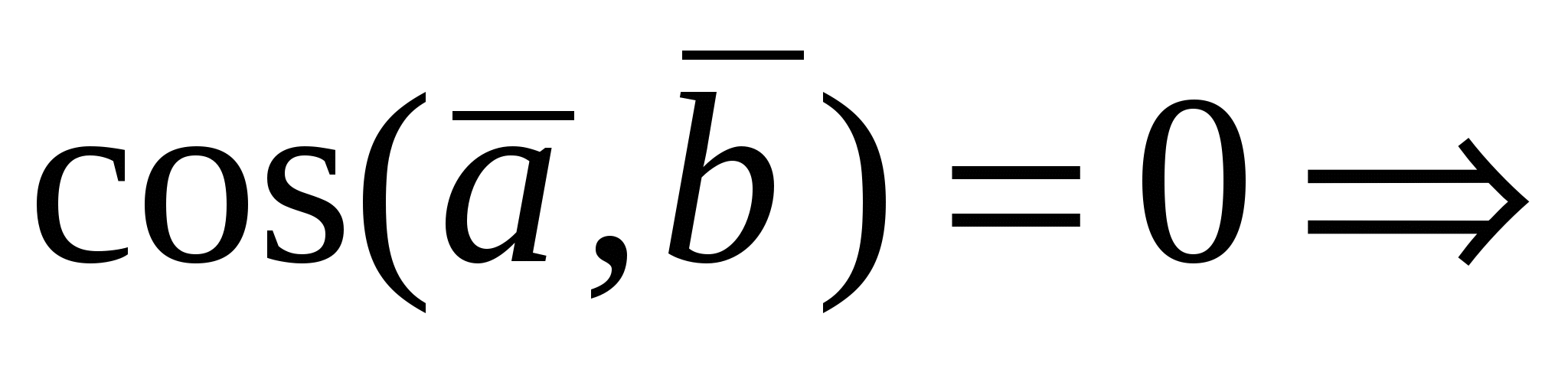 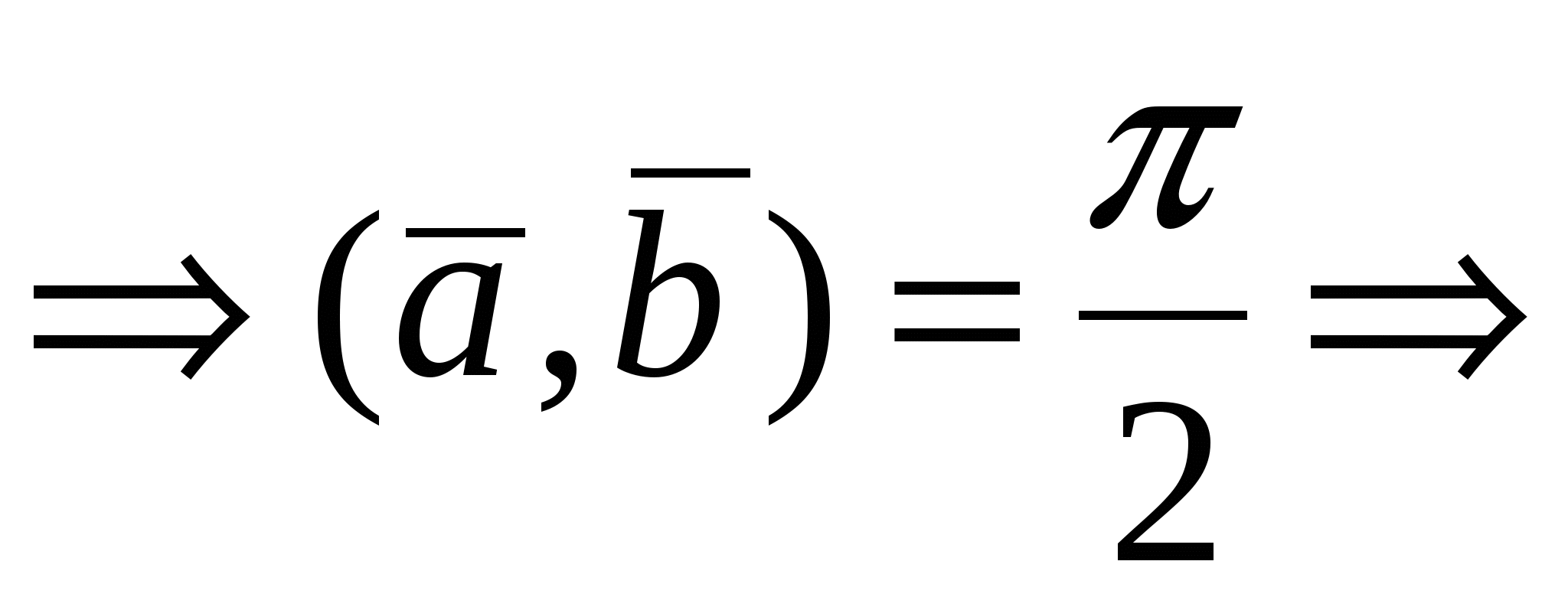 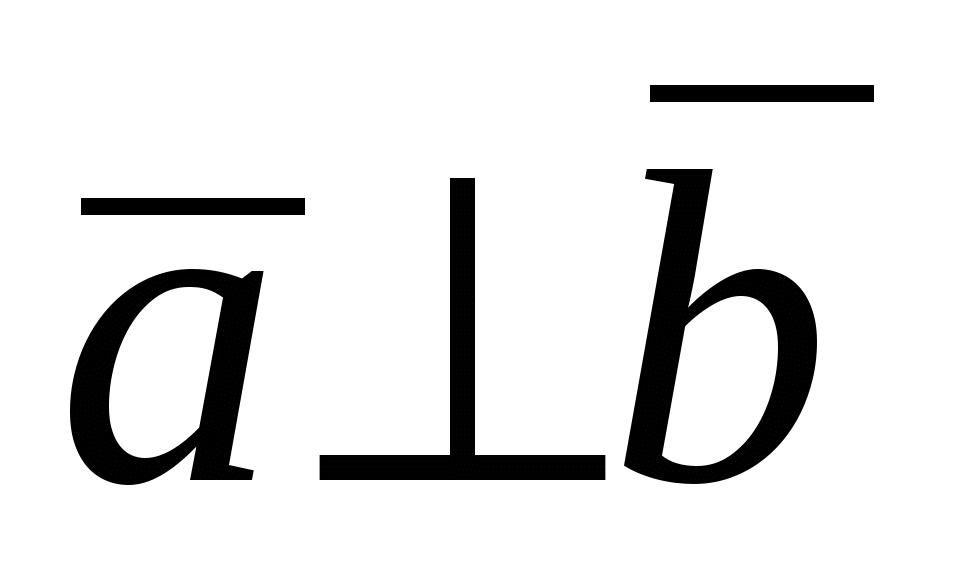 . .

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ В ОРТОНОРМИРОВАННОМ БАЗИСЕ
Теорема. В ортонормированном базисе скалярное произведение векторов  и и 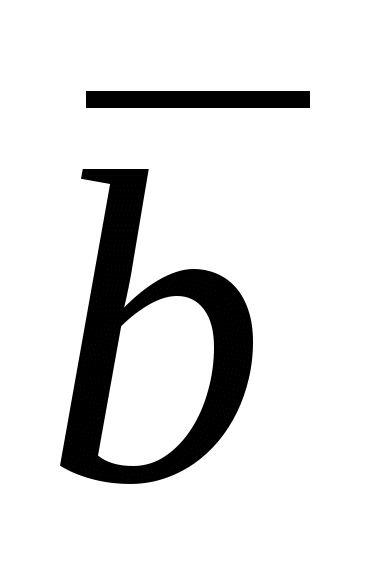 равно сумме произведений одноименных координат множителей. равно сумме произведений одноименных координат множителей.
Доказательство. Пусть в пространстве выбран ортонормированный базис 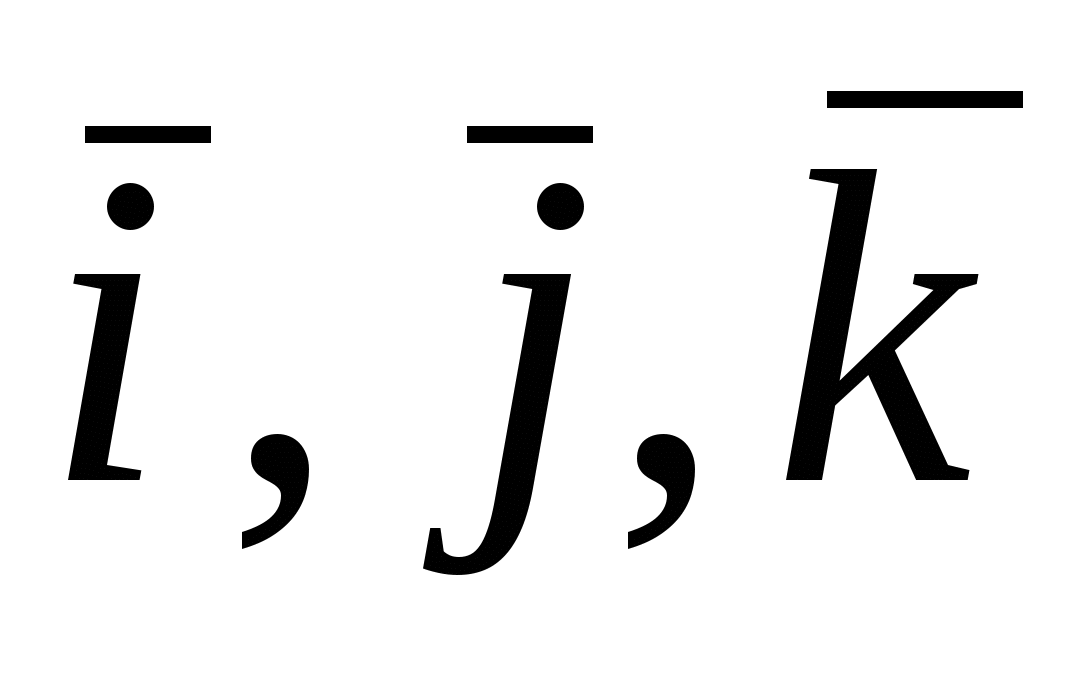 и векторы и векторы  и и 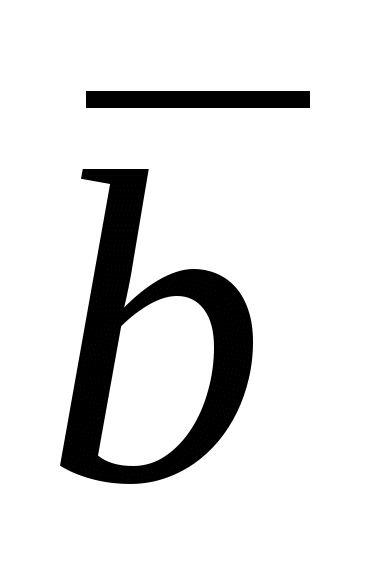 имеют в этом базисе координаты соответственно имеют в этом базисе координаты соответственно 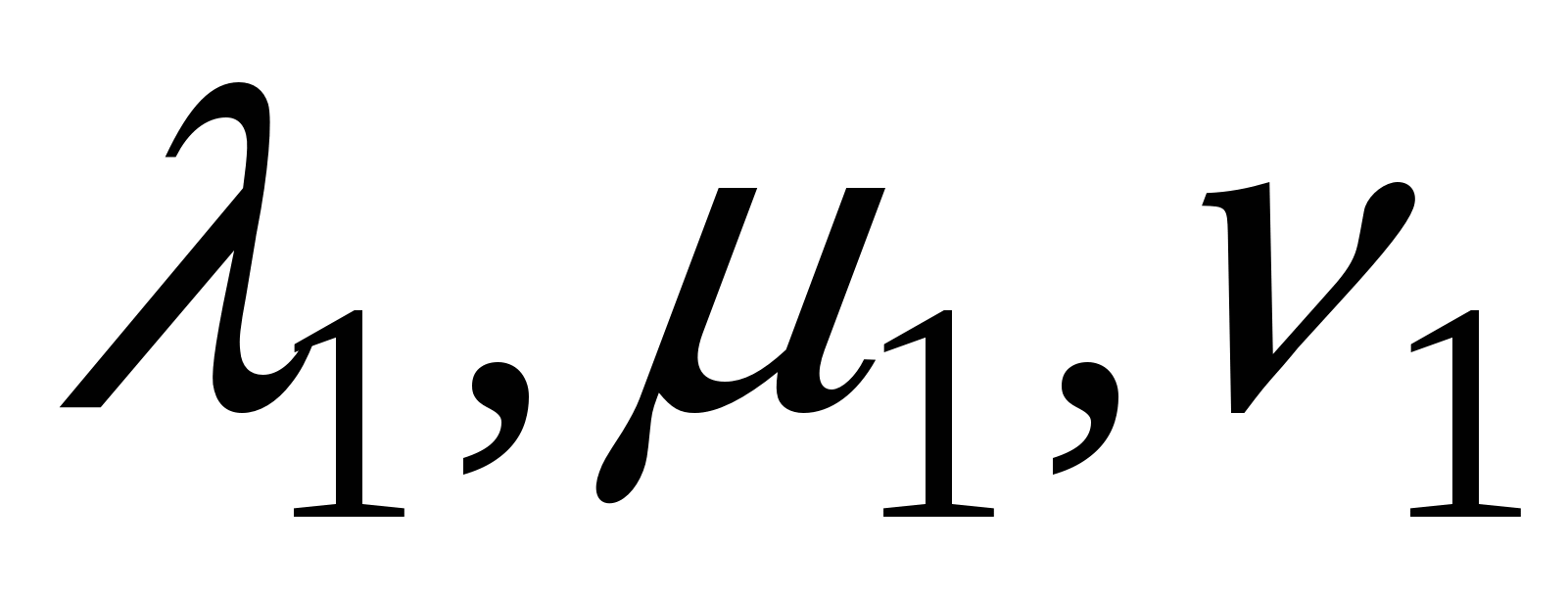  и и 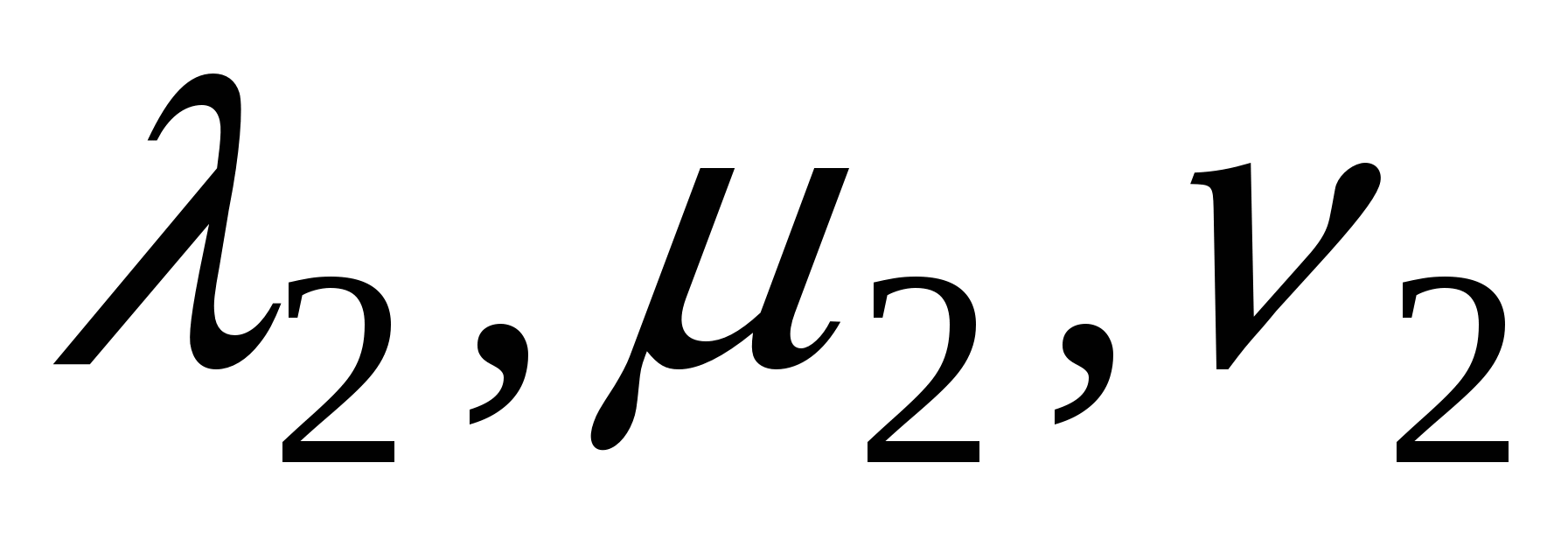 , т.е. , т.е. 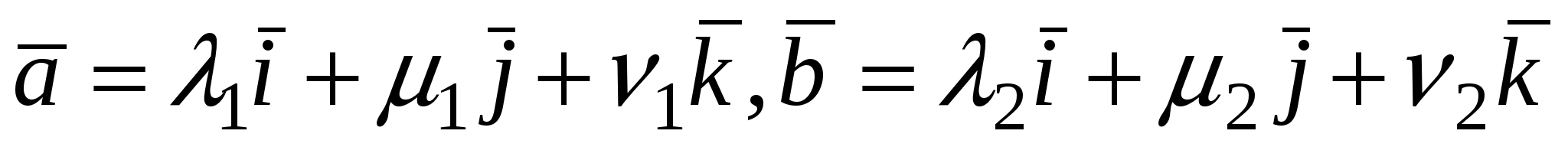 . Тогда, используя свойства скалярного произведения, будем иметь . Тогда, используя свойства скалярного произведения, будем иметь 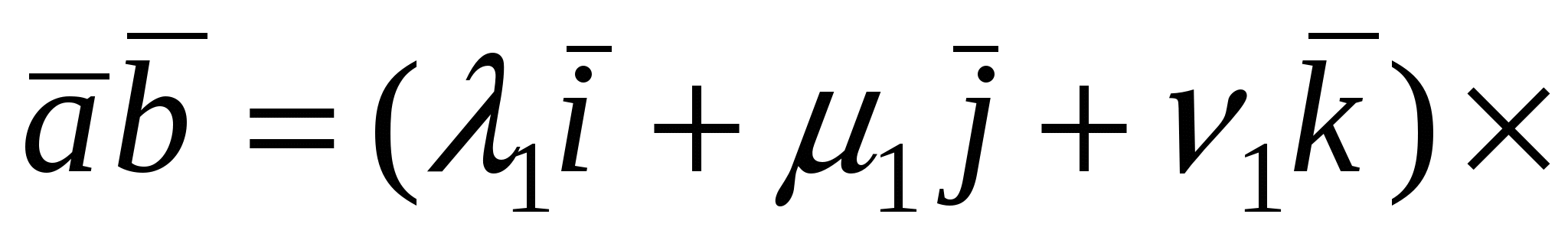 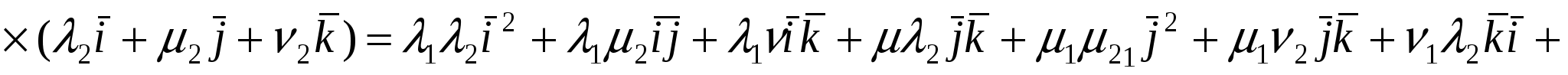 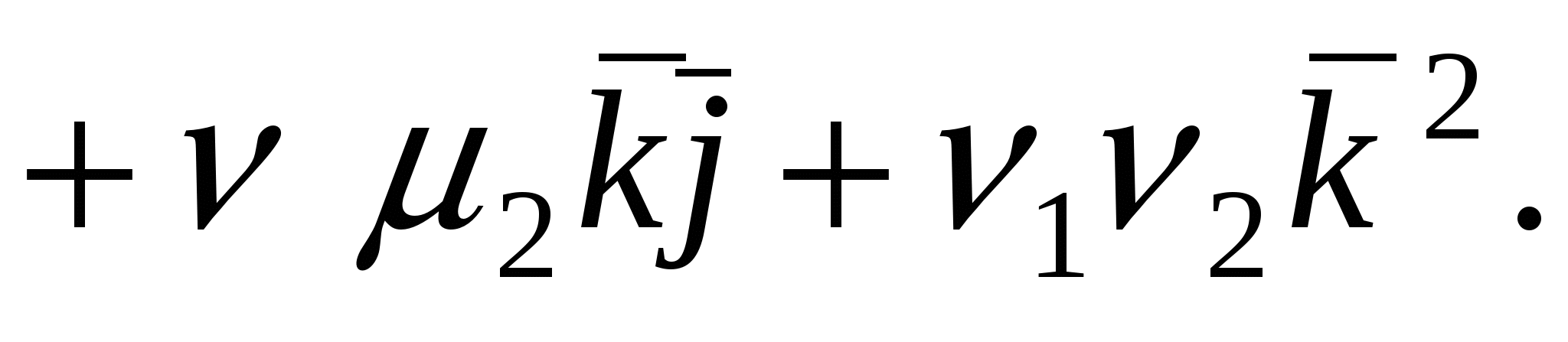
Так как 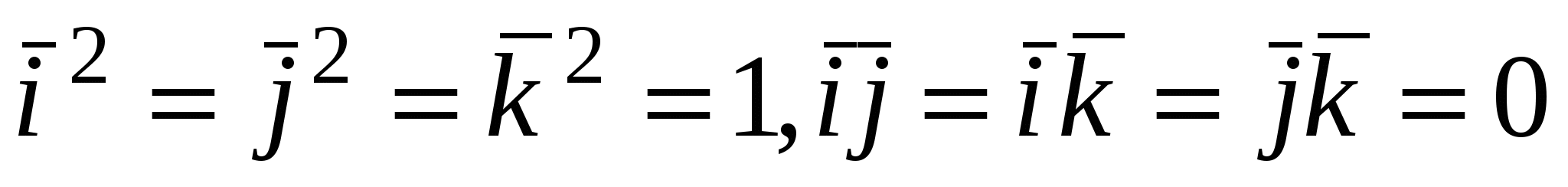 , то окончательно получим: , то окончательно получим:
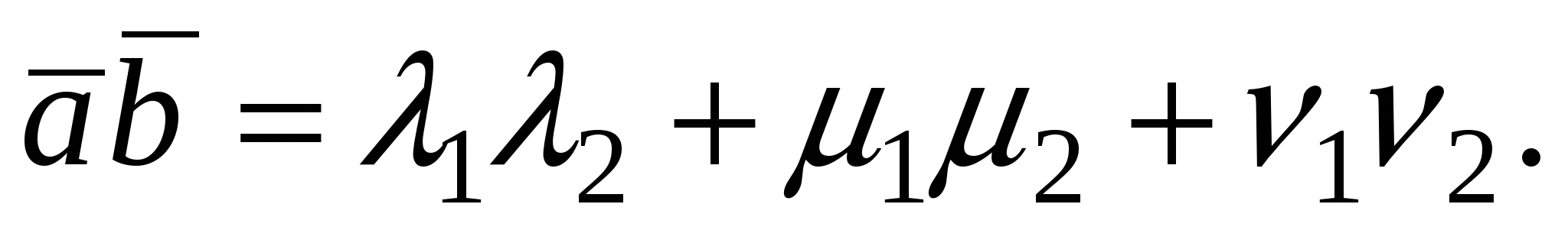
МОДУЛЬ ВЕКТОРА В ОРТОНОРМИРОВАННОМ БАЗИСЕ
Из формулы для скалярного произведения при 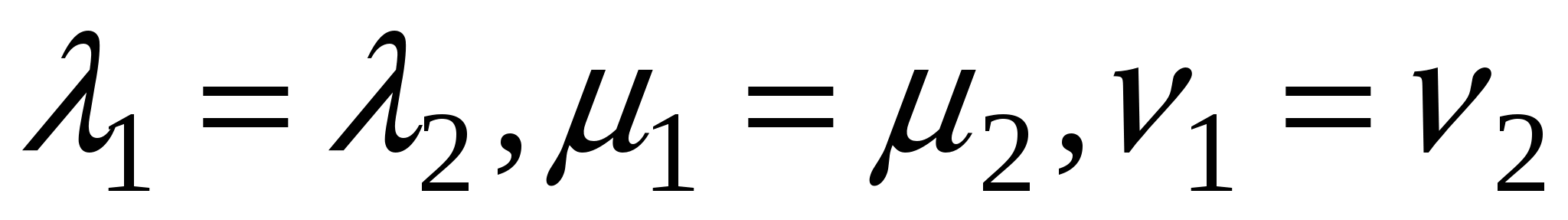 получим получим 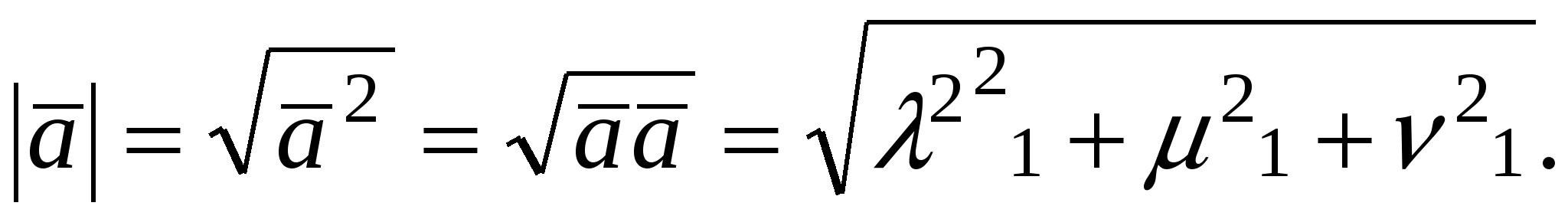
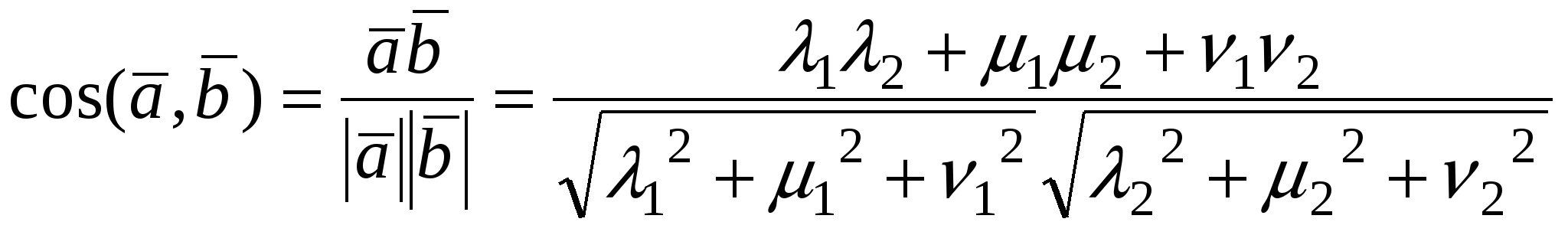 . .
УСЛОВИЕ ОРТОГОНАЛЬНОСТИ ДВУХ ВЕКТОРОВ В
ОРТОНОРМИРОВАННОМ БАЗИСЕ
Если 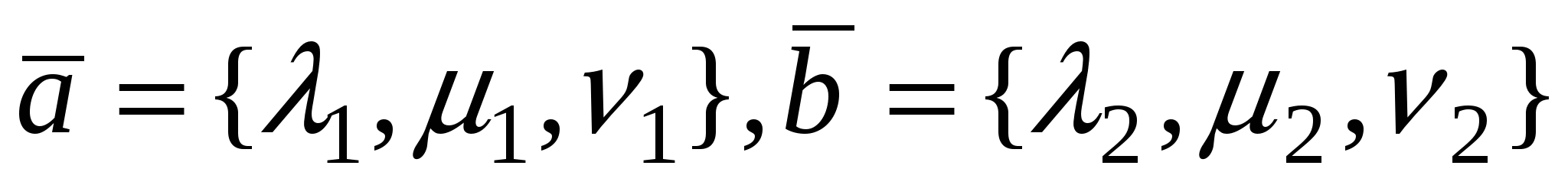 , то необходимое и достаточное условие ортогональности , то необходимое и достаточное условие ортогональности 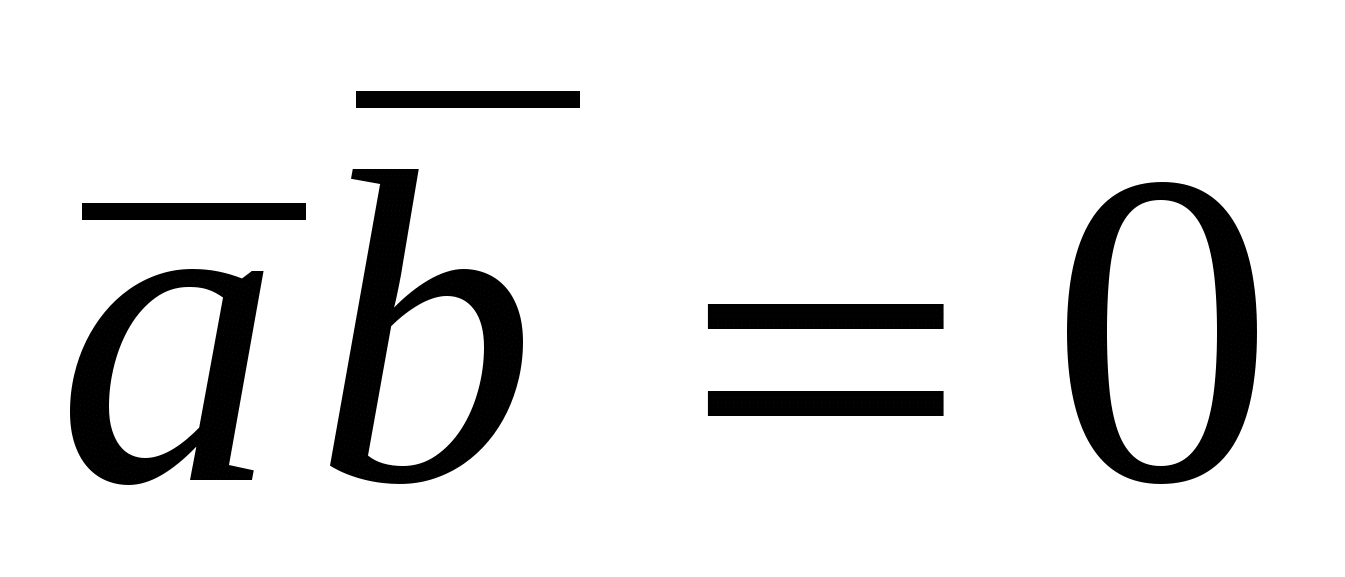 запишется в виде запишется в виде 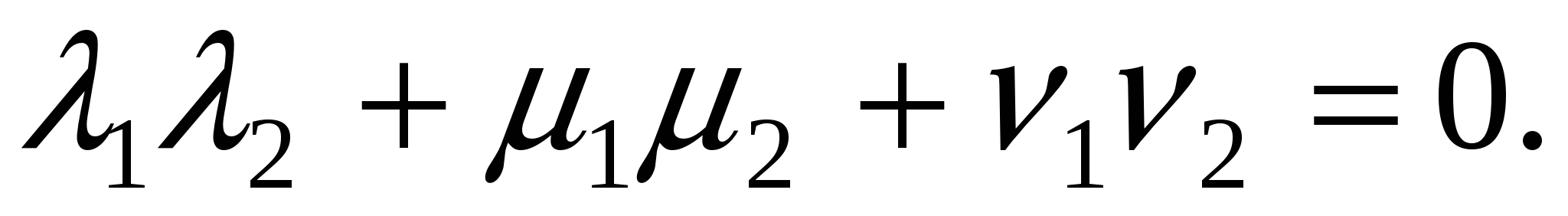 
НАПРАВЛЯЮЩИЕ КОСИНУСЫ ВЕКТОРА
Определение. Направляющими косинусами вектора  в заданном базисе называются косинусы углов между вектором в заданном базисе называются косинусы углов между вектором  и базисными векторами. и базисными векторами.
Пусть 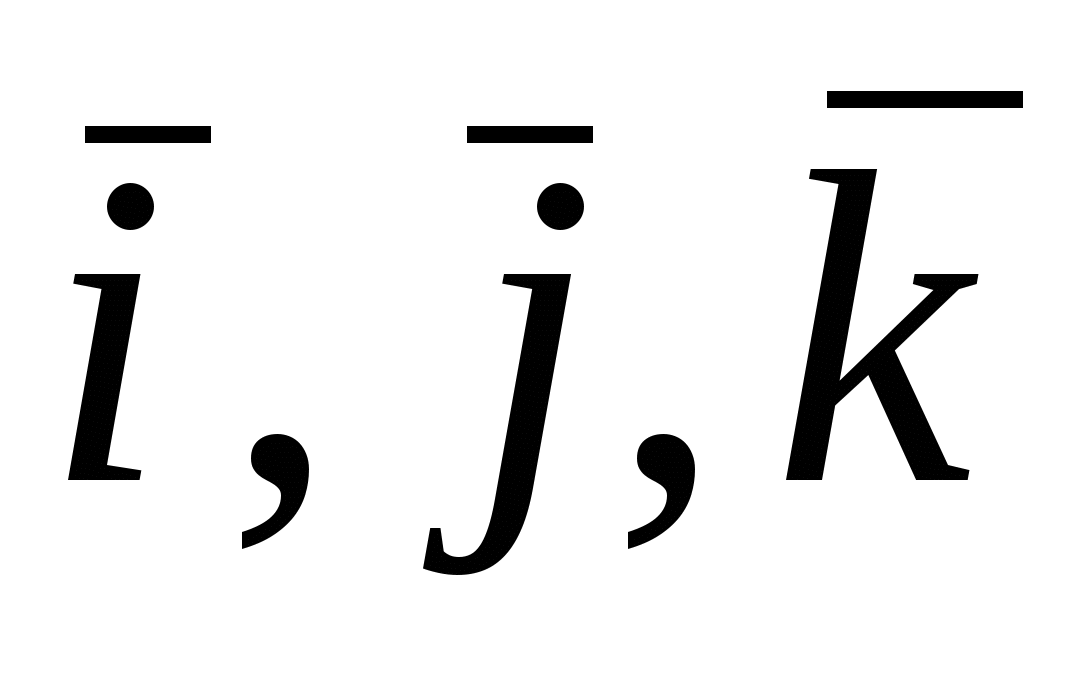 – базисные векторы ортонормированного базиса и – базисные векторы ортонормированного базиса и 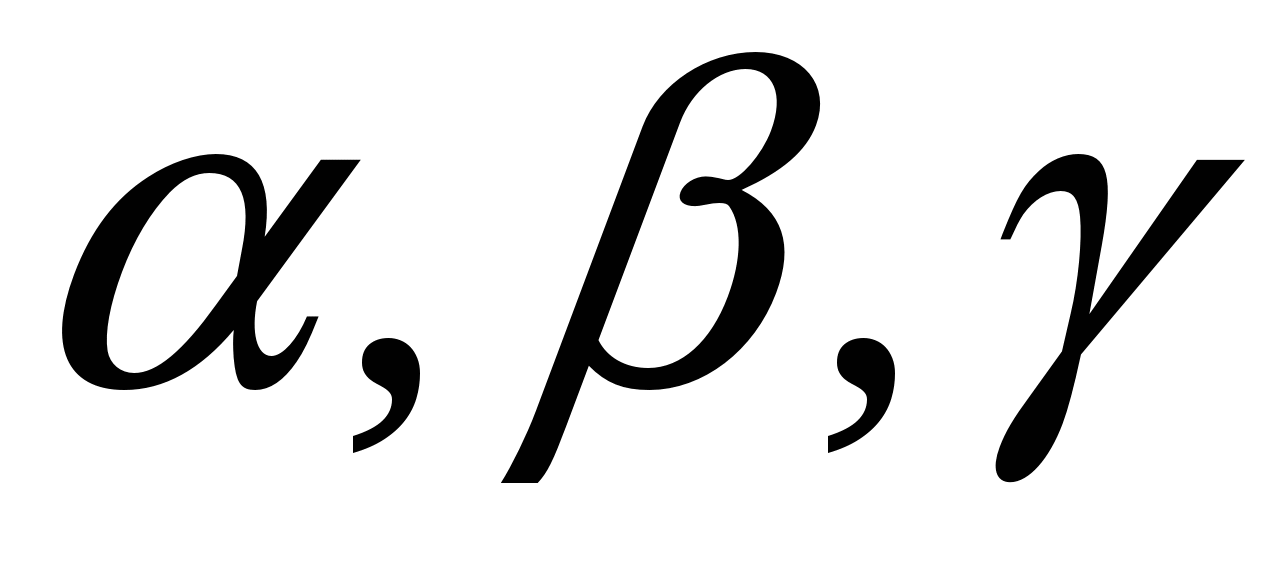 – углы между вектором – углы между вектором  и векторами и векторами 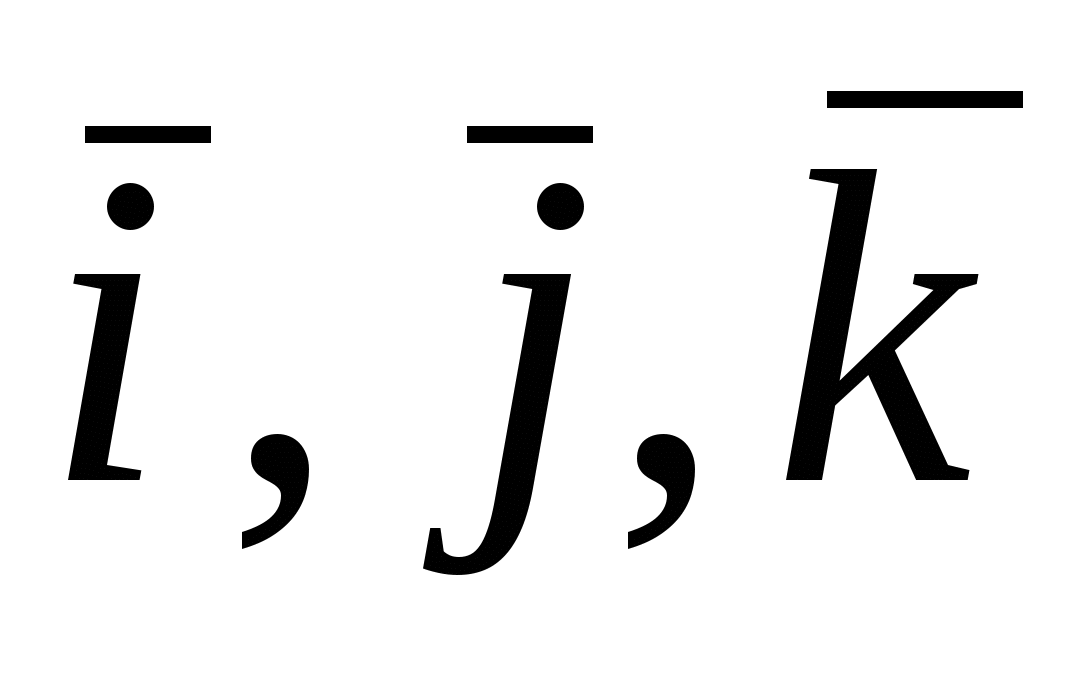 соответственно. соответственно.
Направляющими косинусами вектора   будут будут  . Если . Если 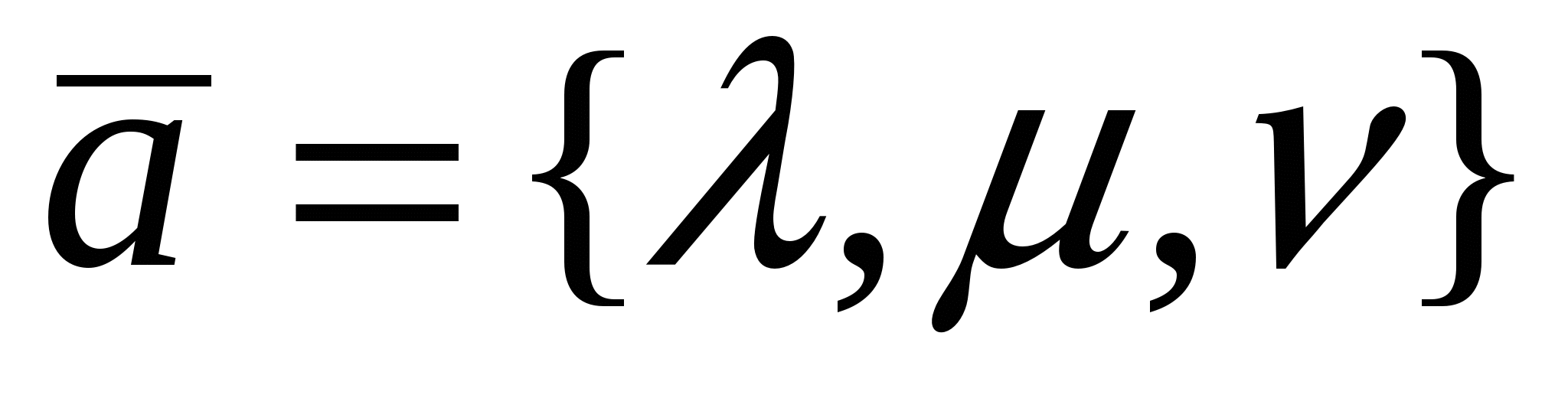 , то из , то из 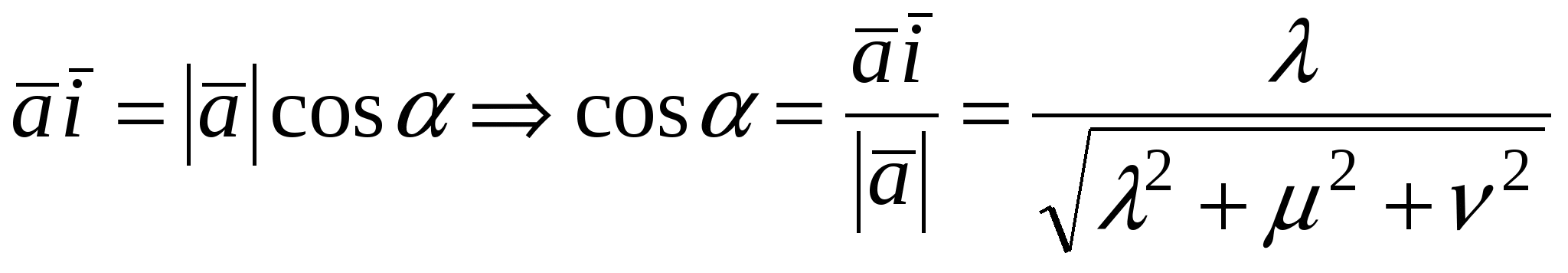 , так как , так как 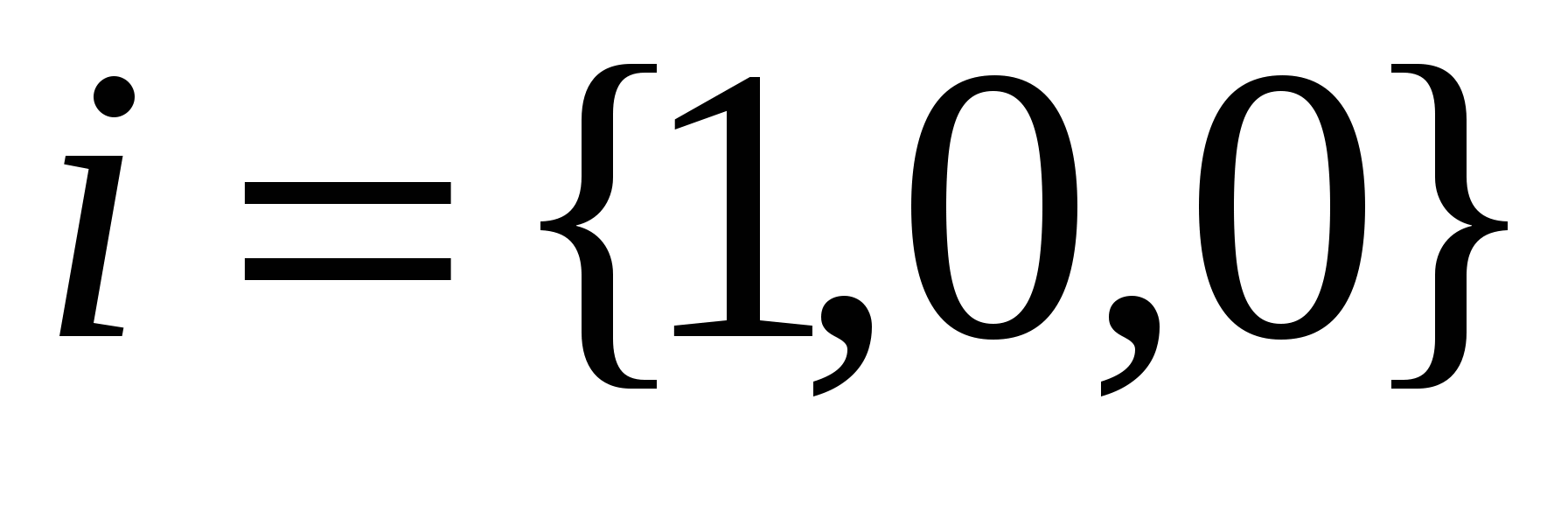 . Аналогично имеем . Аналогично имеем
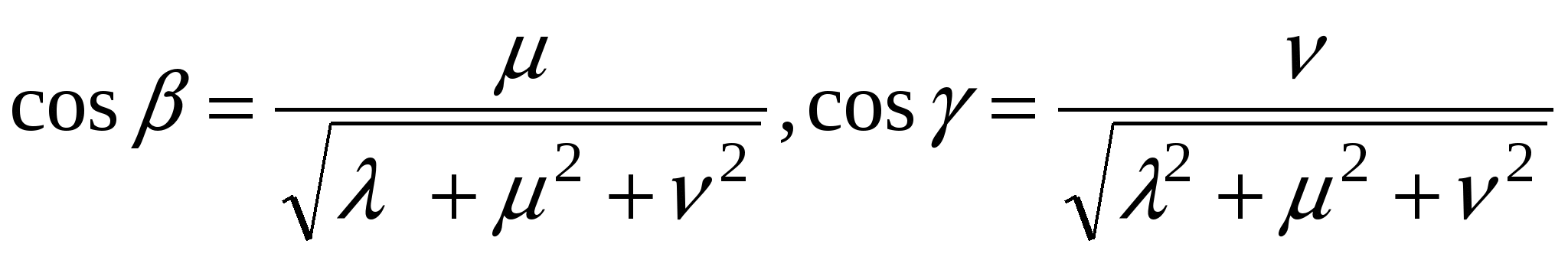 . .
Замечание. Для любого вектора  имеем имеем 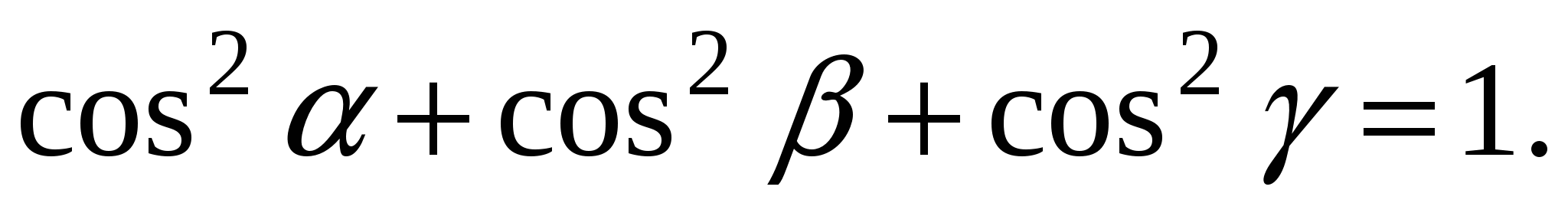
ЛИНЕЙНЫЕ СВОЙСТВА ПРОЕКЦИИ ВЕКТОРА НА ОСЬ
В ортонормированном базисе координаты вектора равны проекциям этого вектора на направления соответствующих базисных векторов.
Действительно, если 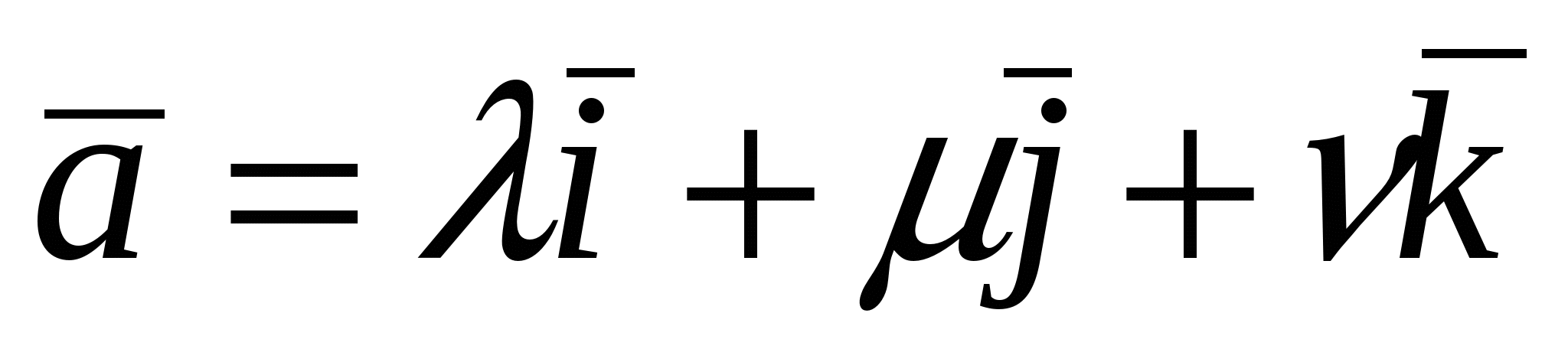 ,то ,то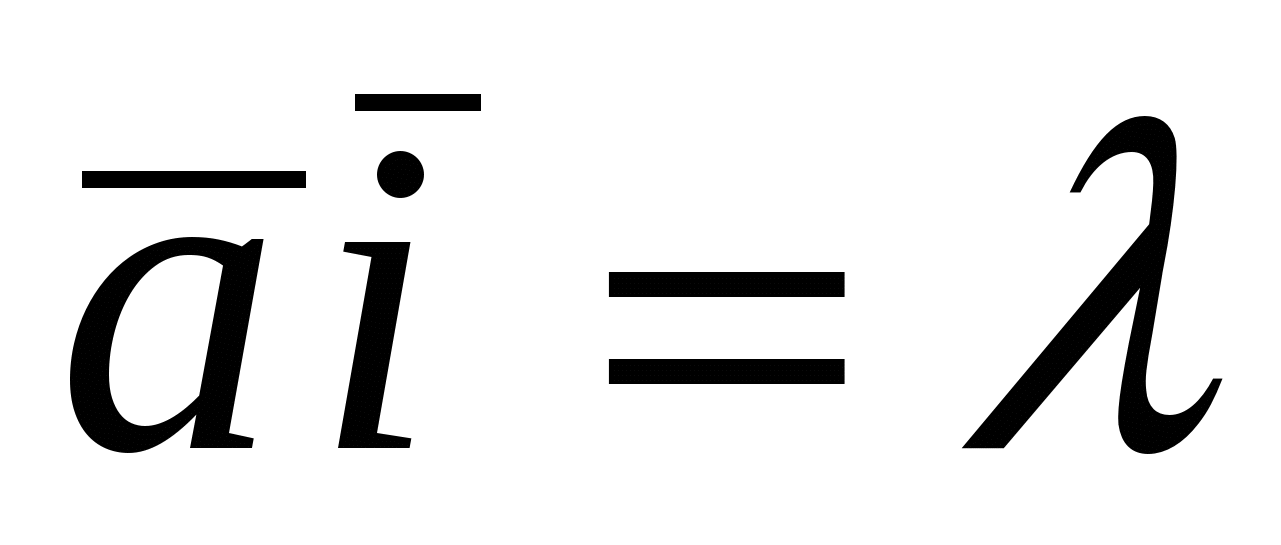 , но , но 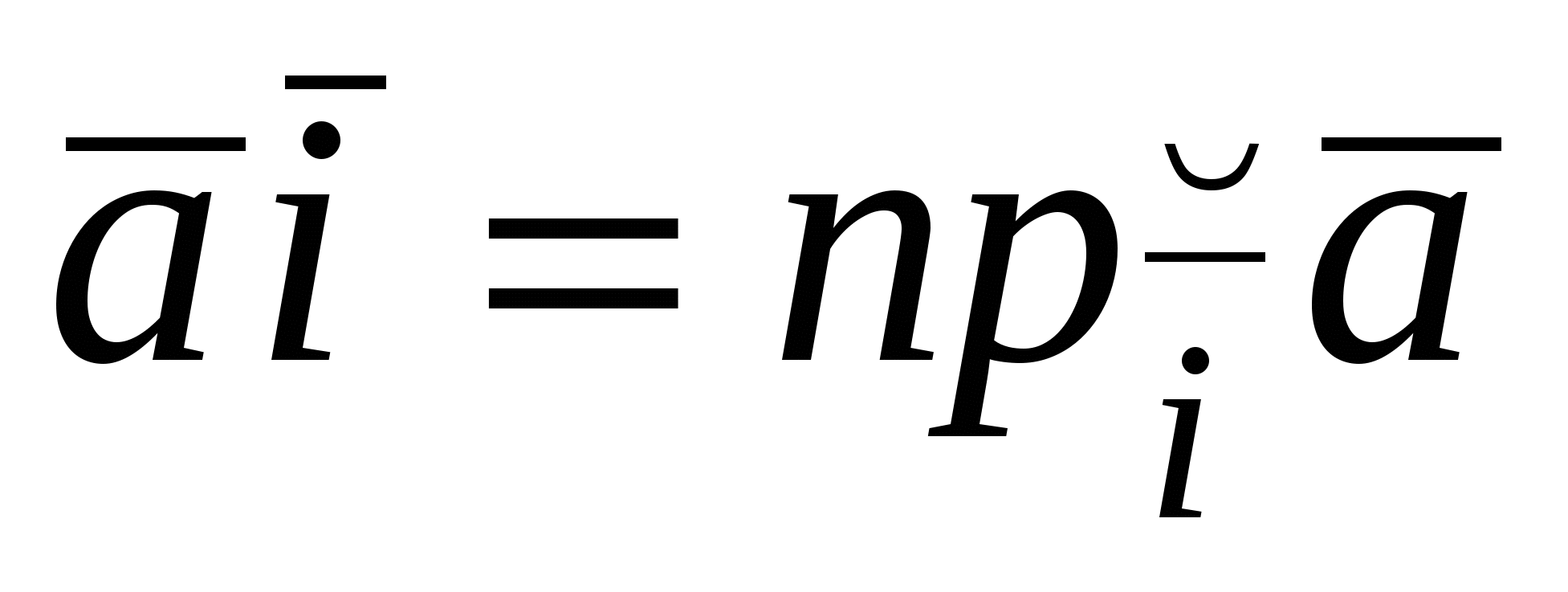 , следовательно, , следовательно, 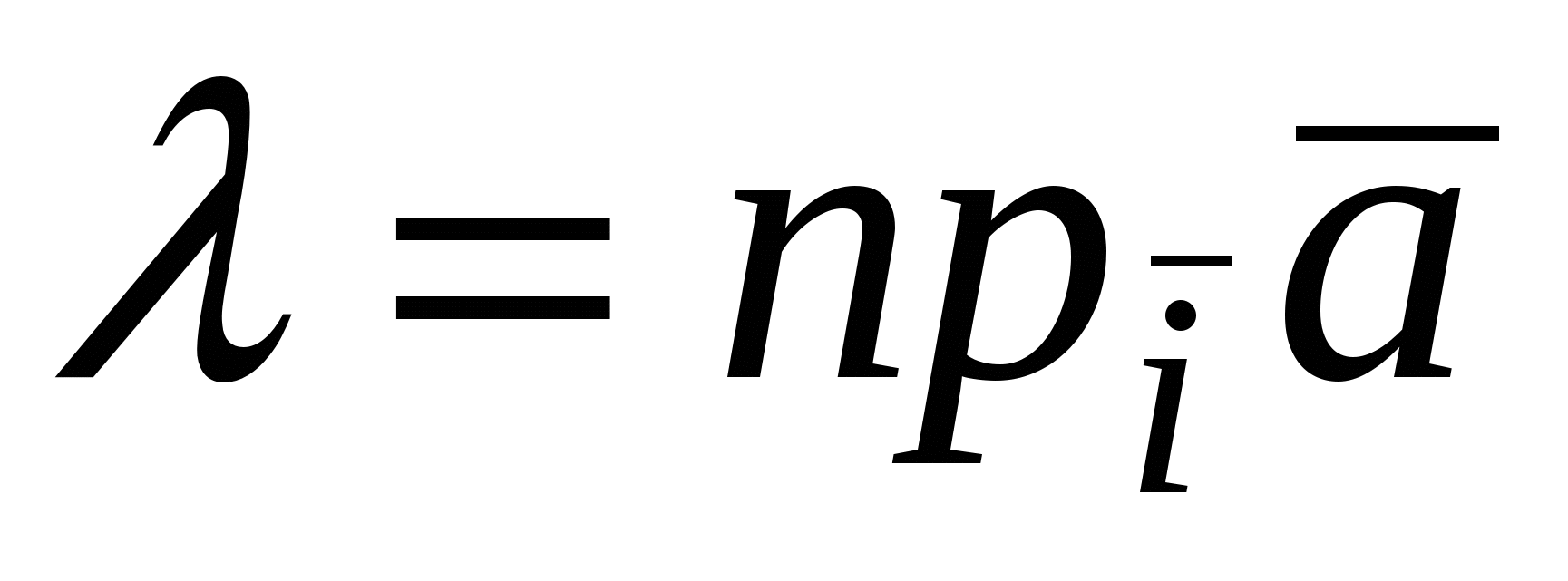 . Аналогично . Аналогично 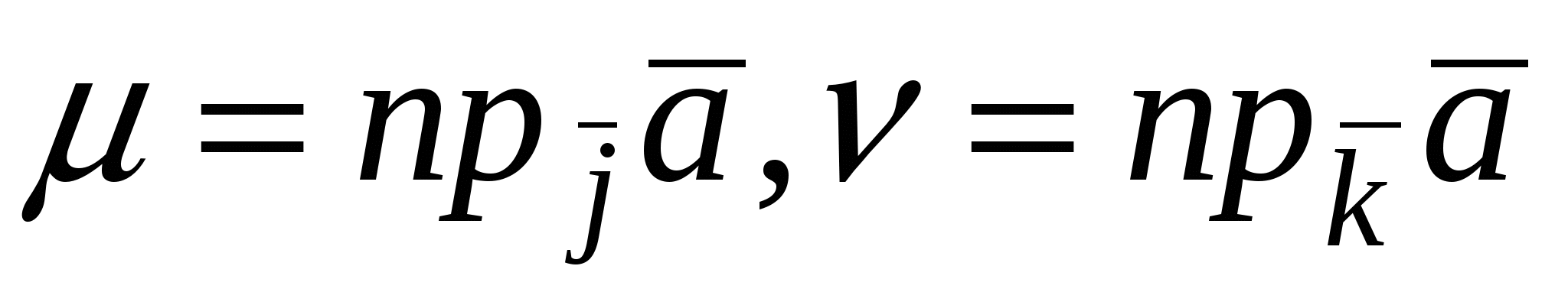 . .
Если 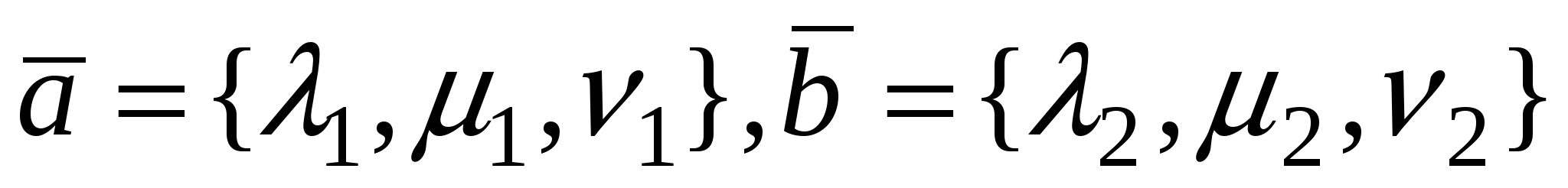 , то из суммы векторов , то из суммы векторов 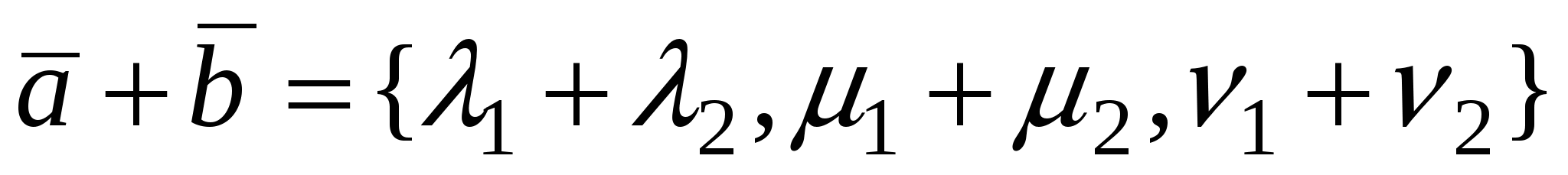 и произведения вектора на число и произведения вектора на число 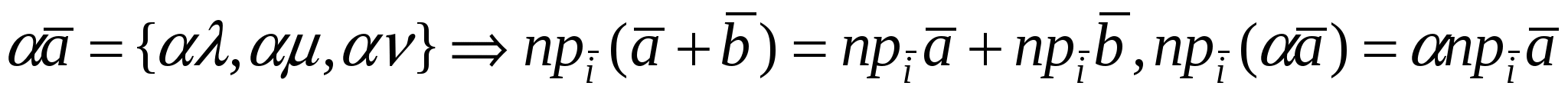 следует, что проекция вектора обладает свойствами линейности. следует, что проекция вектора обладает свойствами линейности.
КОНТРОЛЬНЫЕ ВОПРОСЫ
Дайте определение скалярного произведения векторов.
Выведите условие ортогональности двух векторов.
Докажите формулу скалярного произведения векторов в ортогональном базисе.
Напишите формулу модуля вектора в ортонормированном базисе.
Выведите условие ортогональности двух векторов в ортогональном базисе.
§6. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Векторным произведением вектора  на вектор на вектор 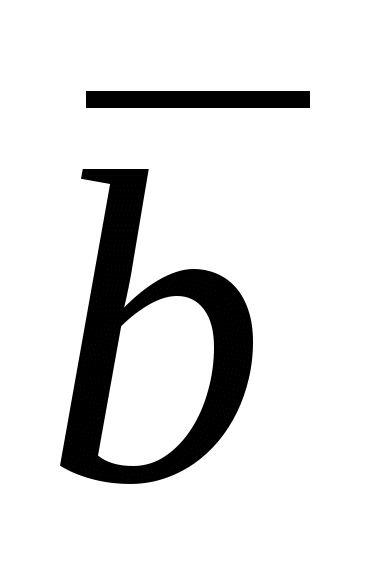 называется новый вектор называется новый вектор 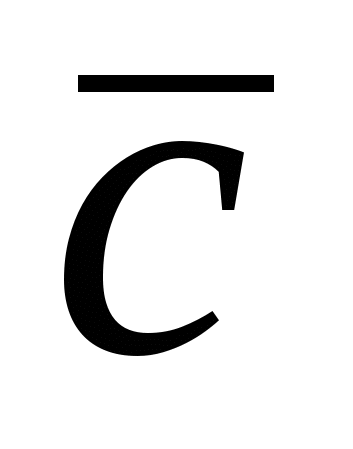 , удовлетворяющий условиям: , удовлетворяющий условиям:
1. 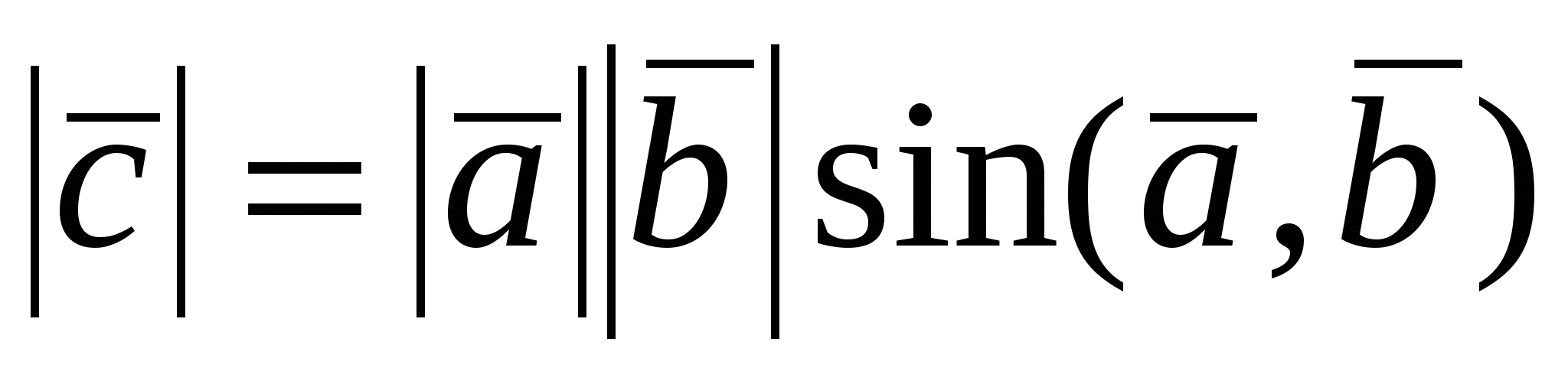 ; ;
2. 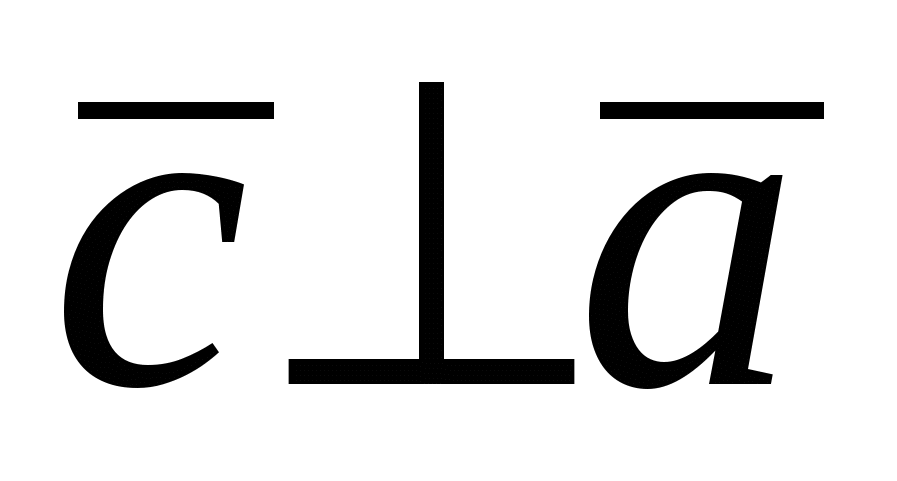 и и 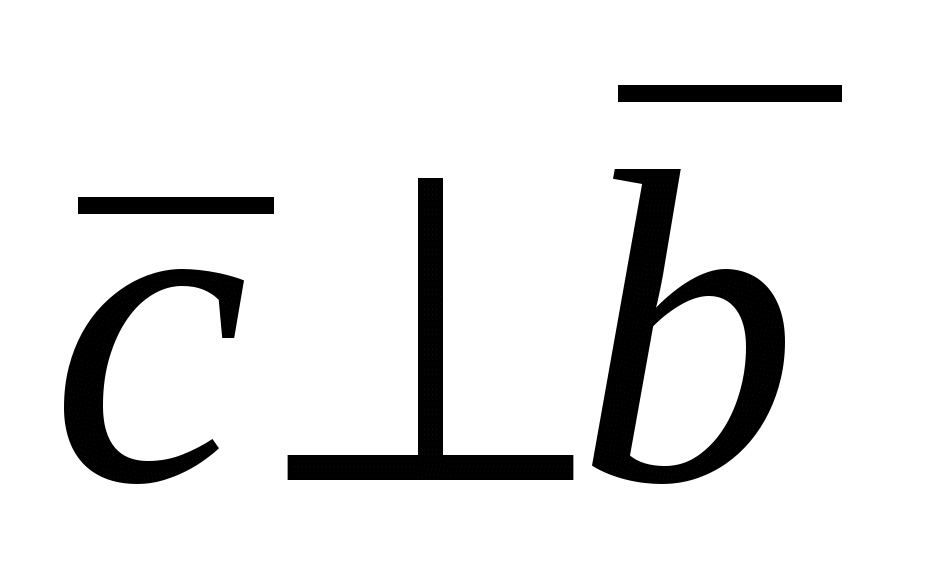 ; ;
3. Упорядоченная тройка векторов 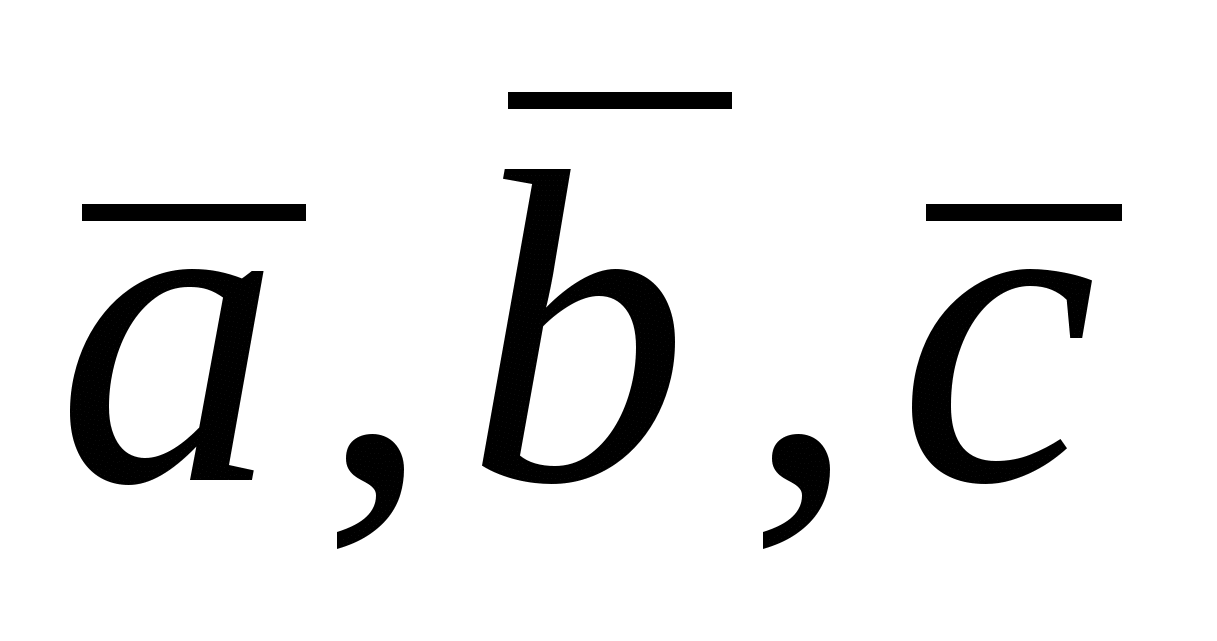 образует правую тройку (с конца вектора образует правую тройку (с конца вектора 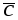 поворот на наименьший угол от первого сомножителя ко второму виден совершающимся против часовой стрелки (рис. 14)). поворот на наименьший угол от первого сомножителя ко второму виден совершающимся против часовой стрелки (рис. 14)).
Векторное произведение  на на 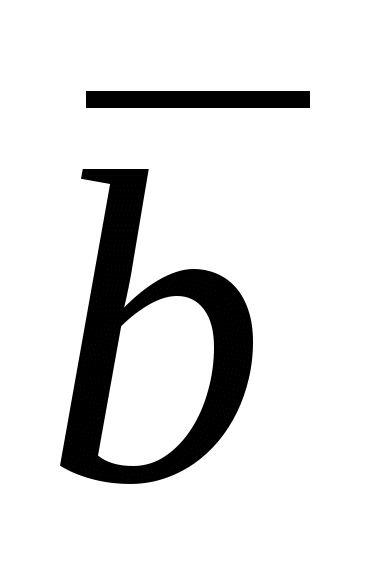 обозначается символом обозначается символом 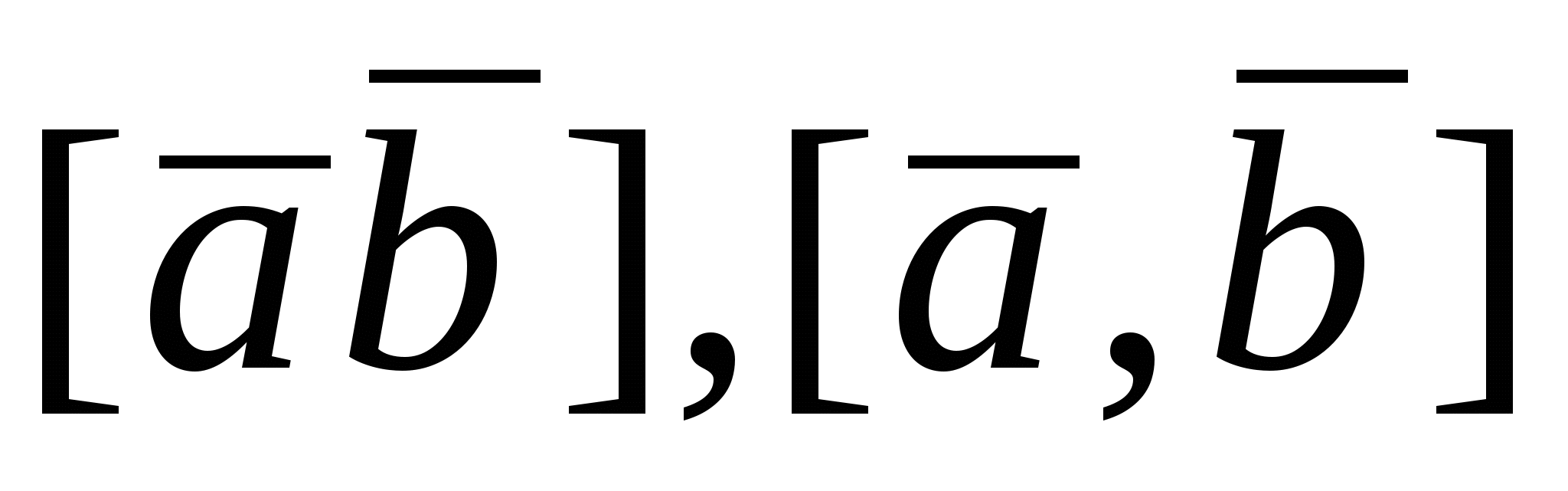 или или 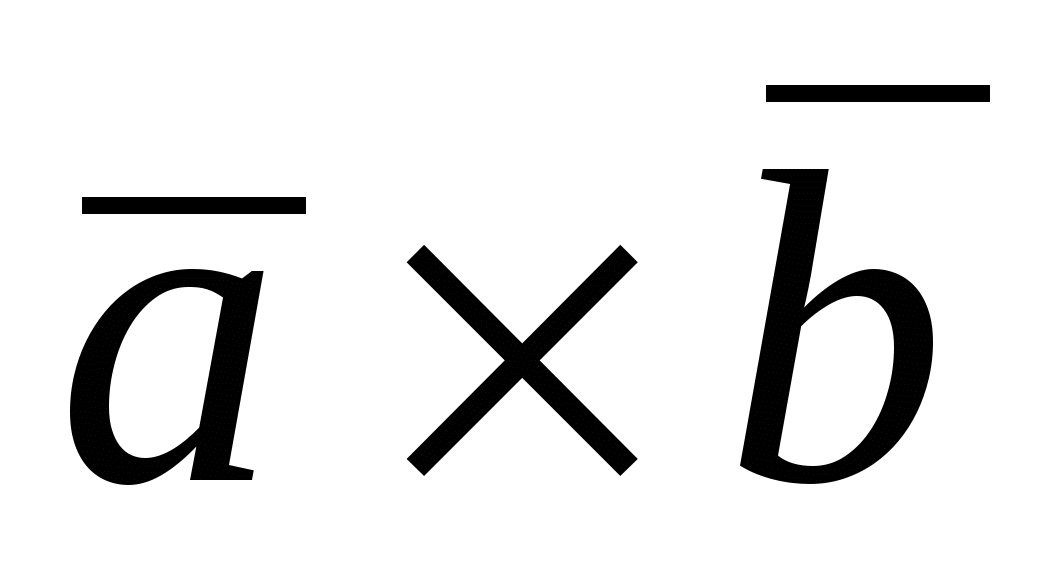 . .
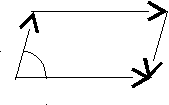 D C D C
A  B B
Рис. 15.
|
 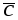
  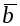
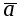
 Рис. 14. Рис. 14.
|
Замечания. 1. Модуль 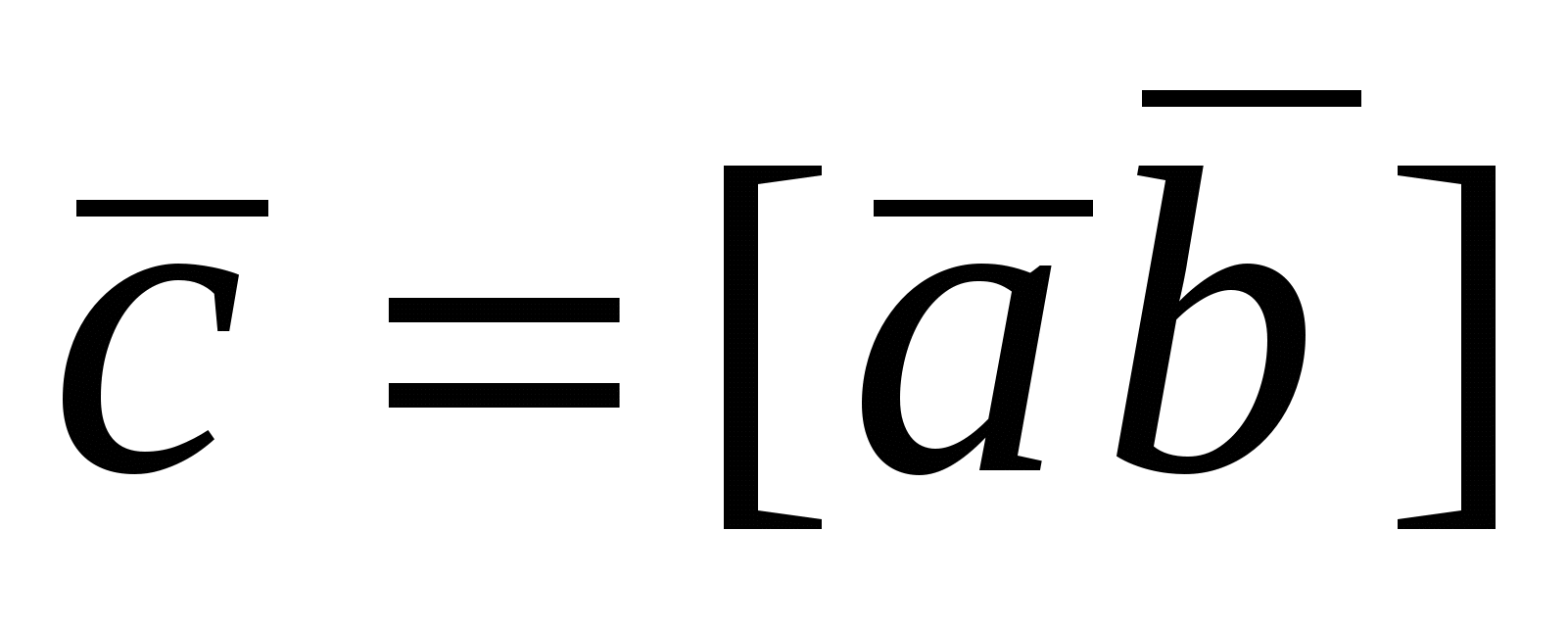 численно равен площади параллелограмма, построенного на векторах численно равен площади параллелограмма, построенного на векторах  и и 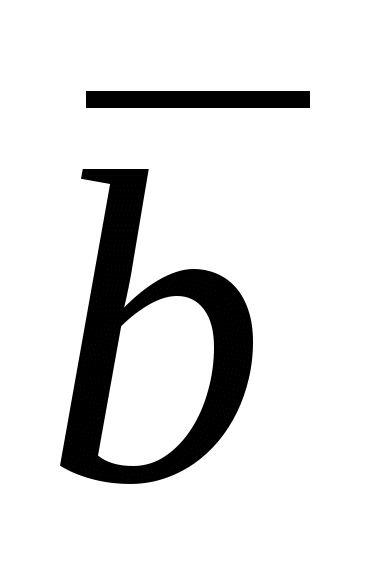 (рис. 15). Действительно, площадь параллелограмма ABCD равна (рис. 15). Действительно, площадь параллелограмма ABCD равна 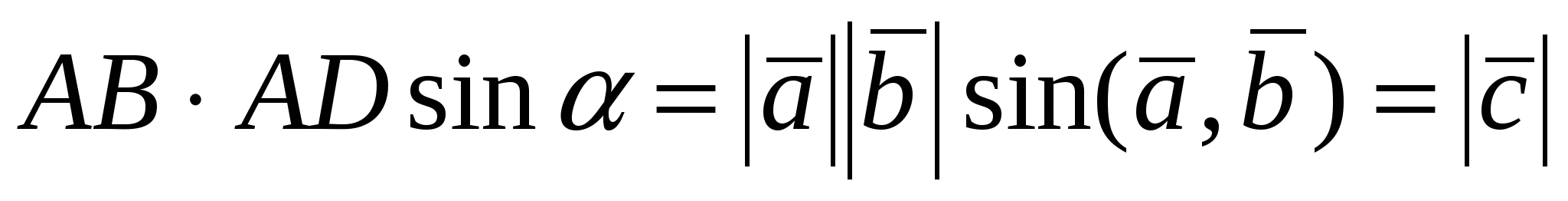
Векторы  и и 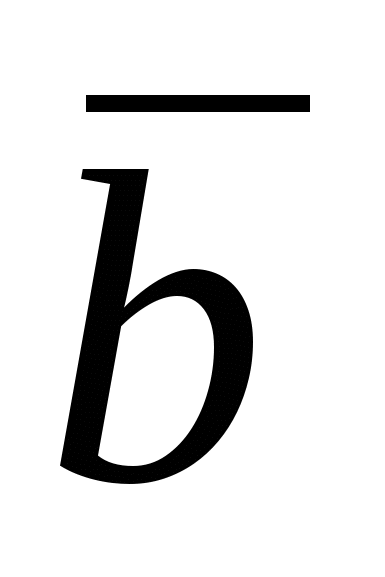 коллинеарны тогда и только тогда, когда коллинеарны тогда и только тогда, когда 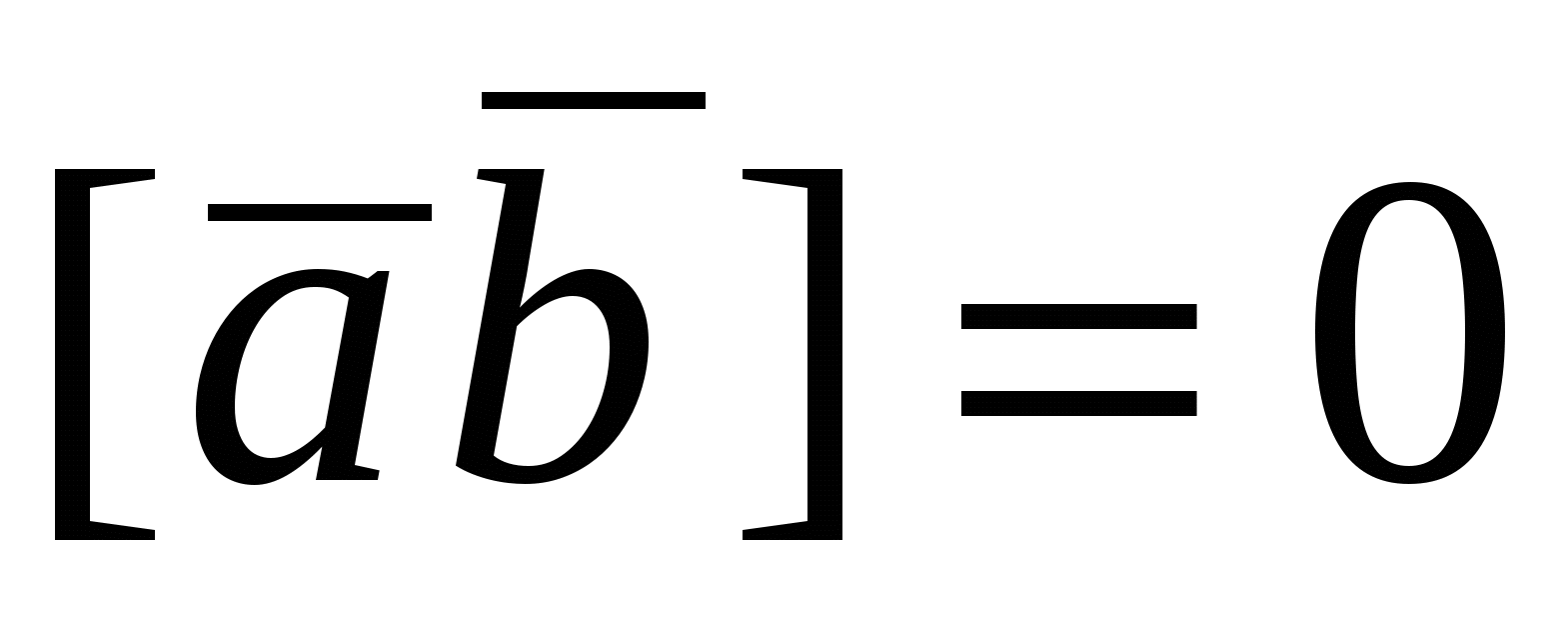 . Необходимость и достаточность этого условия следует из определения векторного произведения. . Необходимость и достаточность этого условия следует из определения векторного произведения.
СВОЙСТВА ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ
1. 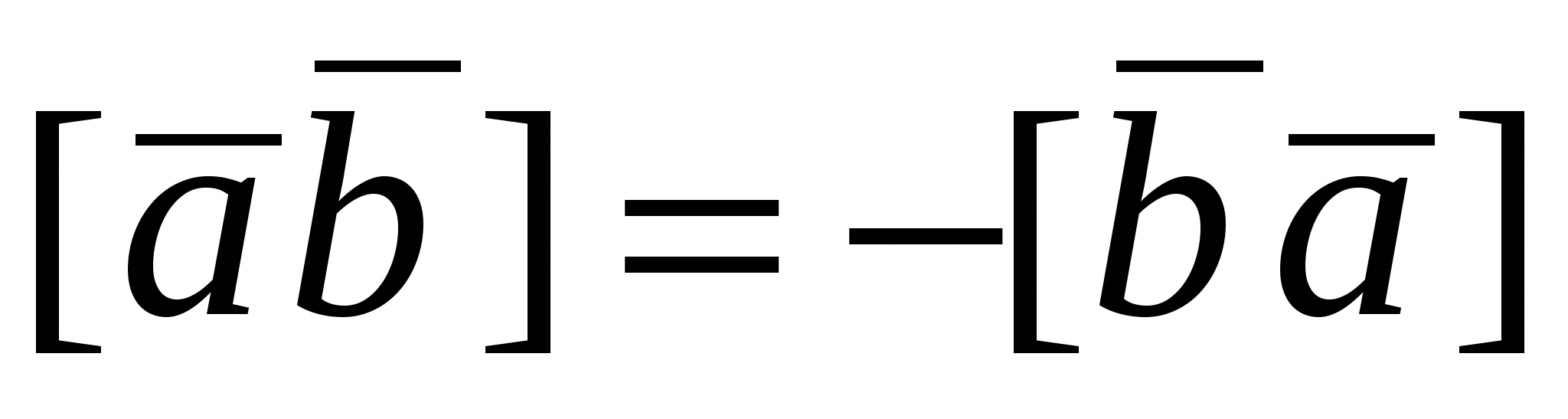 (антикоммутативность); (антикоммутативность);
2. 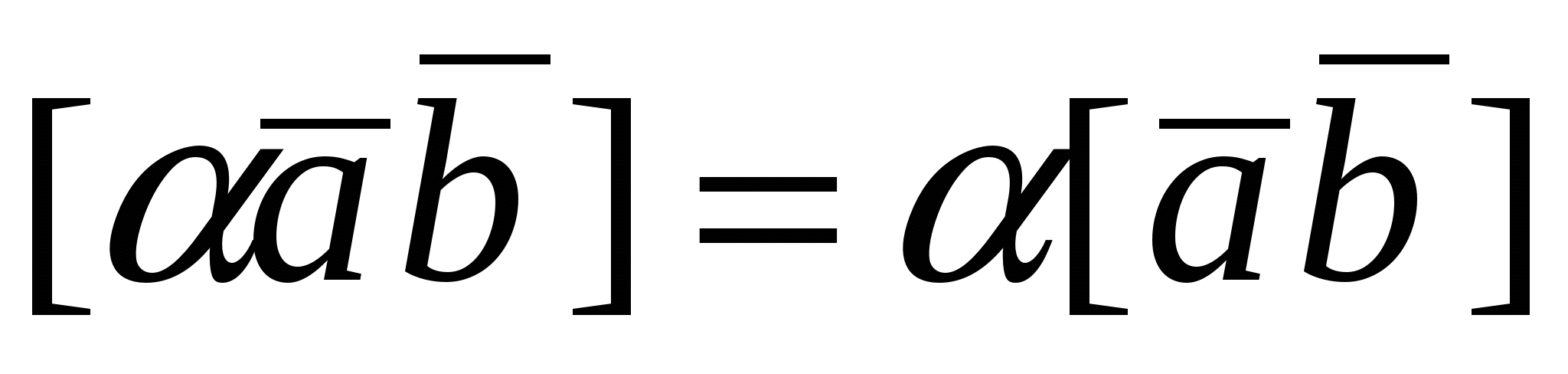 (ассоциативность относительно числового множителя); (ассоциативность относительно числового множителя);
3. 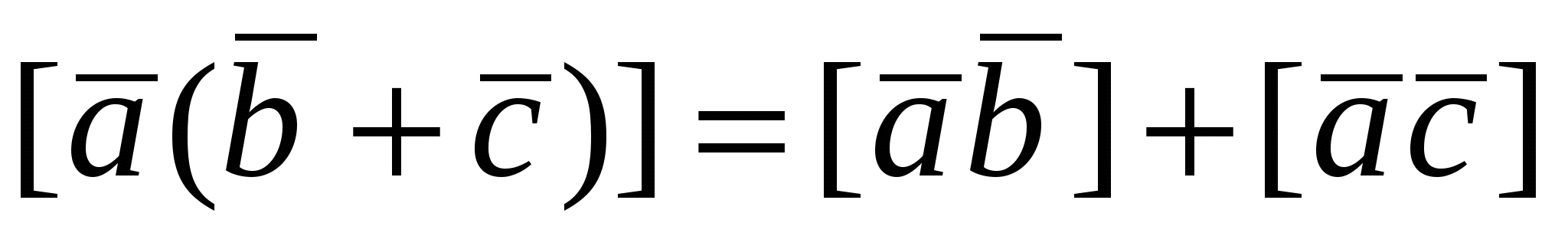 (дистрибутивность относительно суммы векторов). (дистрибутивность относительно суммы векторов).
Это свойство примем без доказательства.
ДОКАЗАТЕЛЬСТВО СВОЙСТВ ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ
1. Пусть 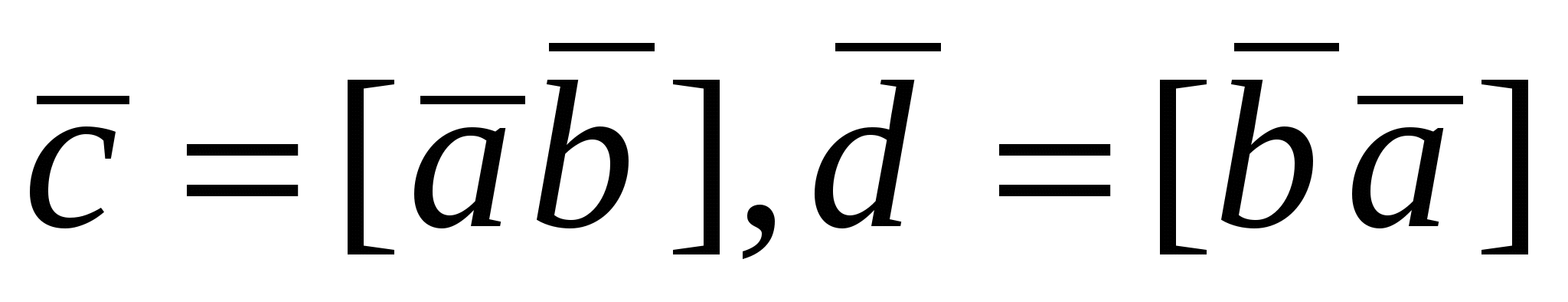 , тогда из , тогда из 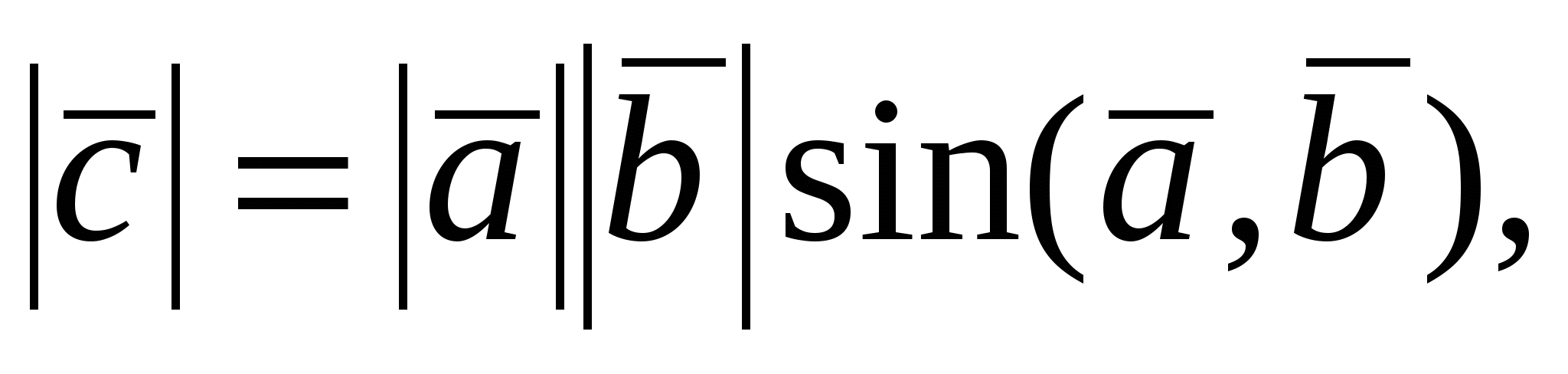 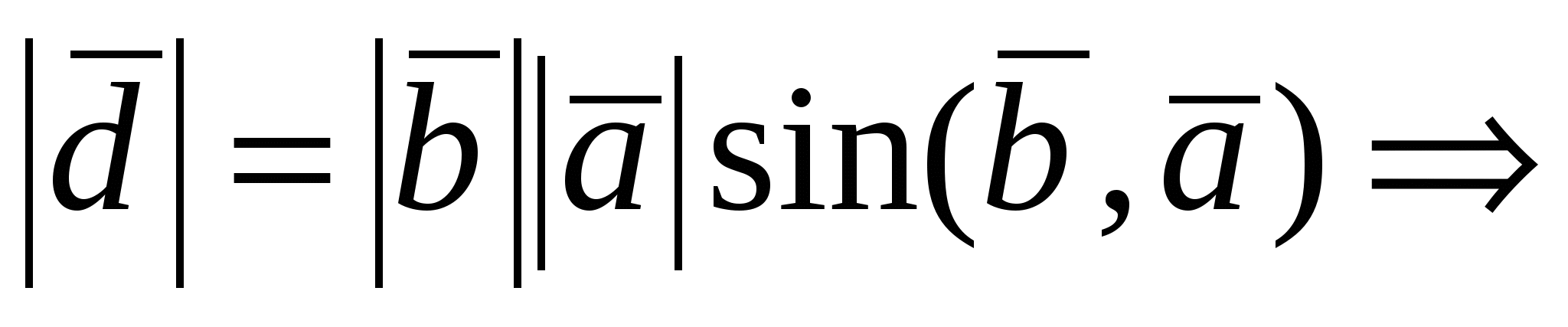 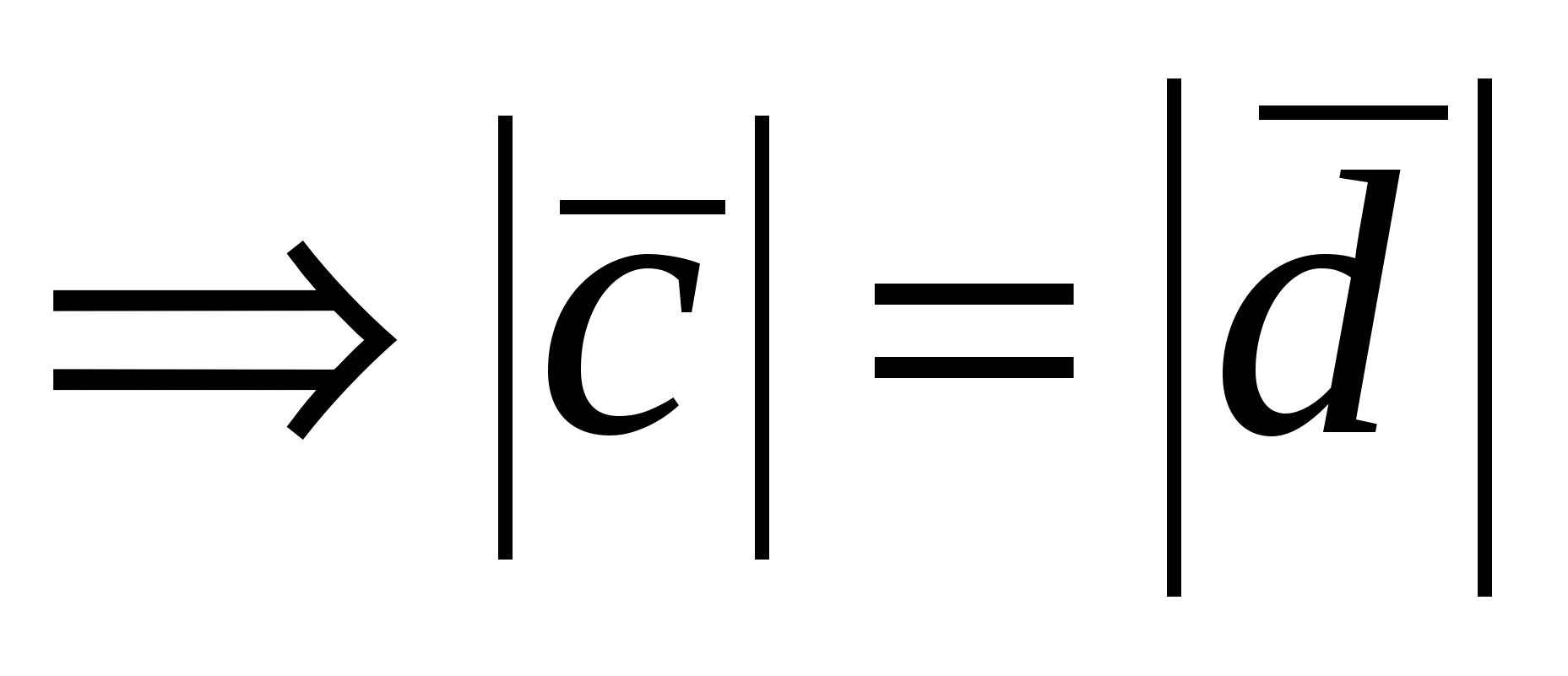 . Векторы . Векторы 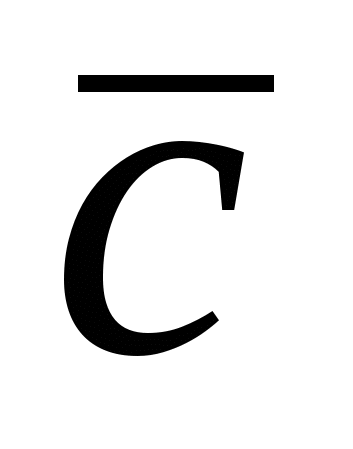 и и 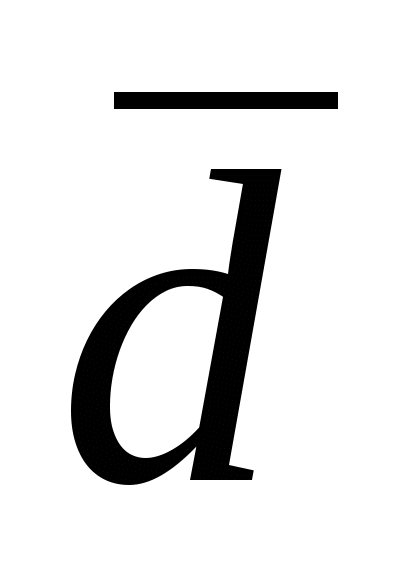 ортогональны плоскости, в которой лежат векторы ортогональны плоскости, в которой лежат векторы  и и 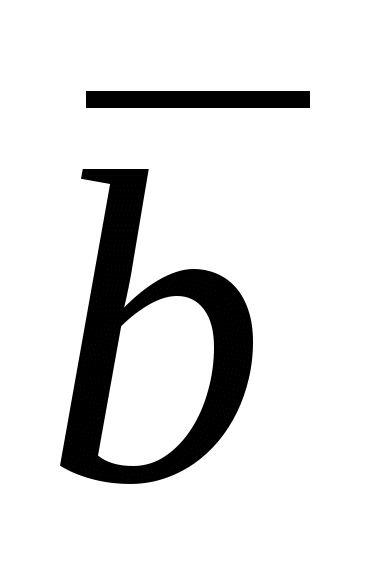 , следовательно, , следовательно, 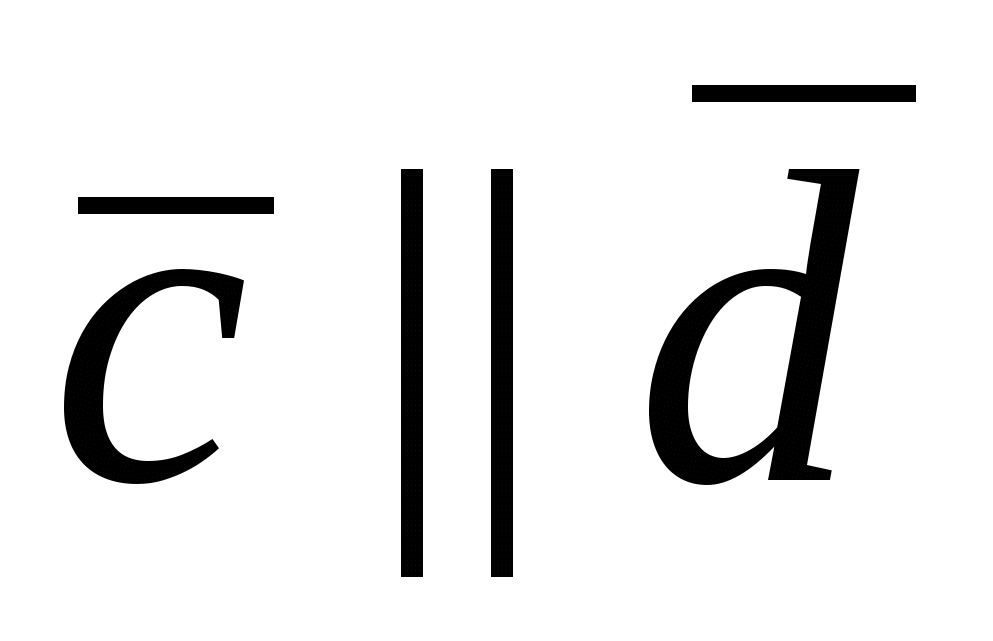 . .
По определению с конца вектора 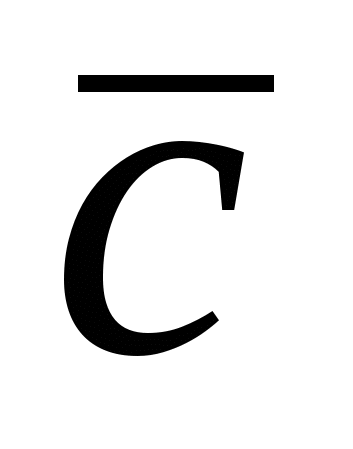 поворот от вектора поворот от вектора  к вектору к вектору 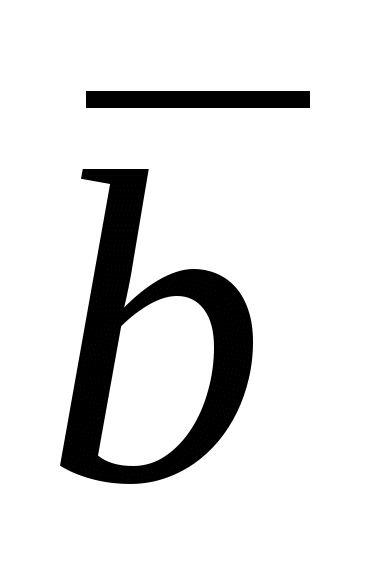 виден совершающимся против часовой стрелки, а с конца вектора виден совершающимся против часовой стрелки, а с конца вектора 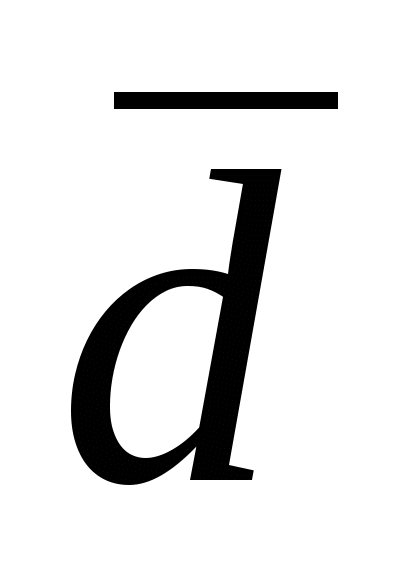 поворот от вектора поворот от вектора 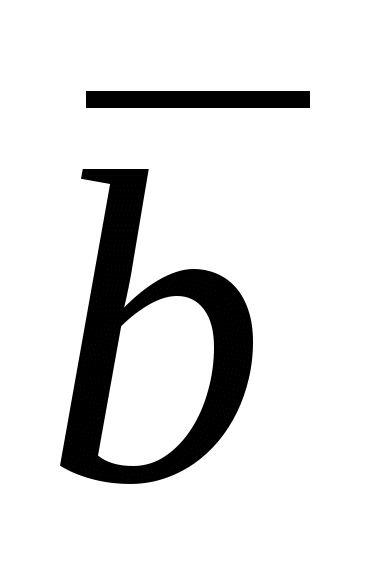 к вектору к вектору  виден совершающимся против часовой стрелки, а это возможно при виден совершающимся против часовой стрелки, а это возможно при  . .
Следовательно, имеем, что 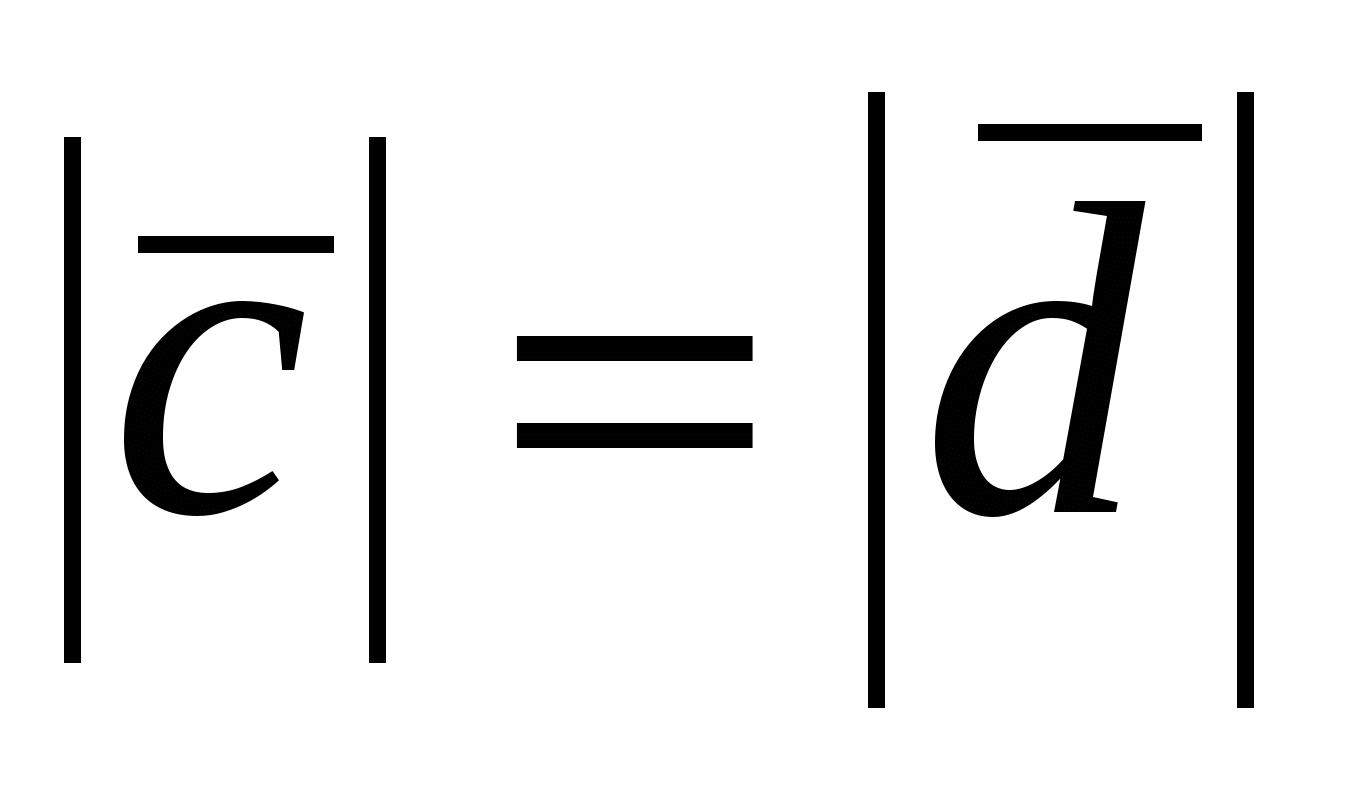 и и  , т. е. , т. е. 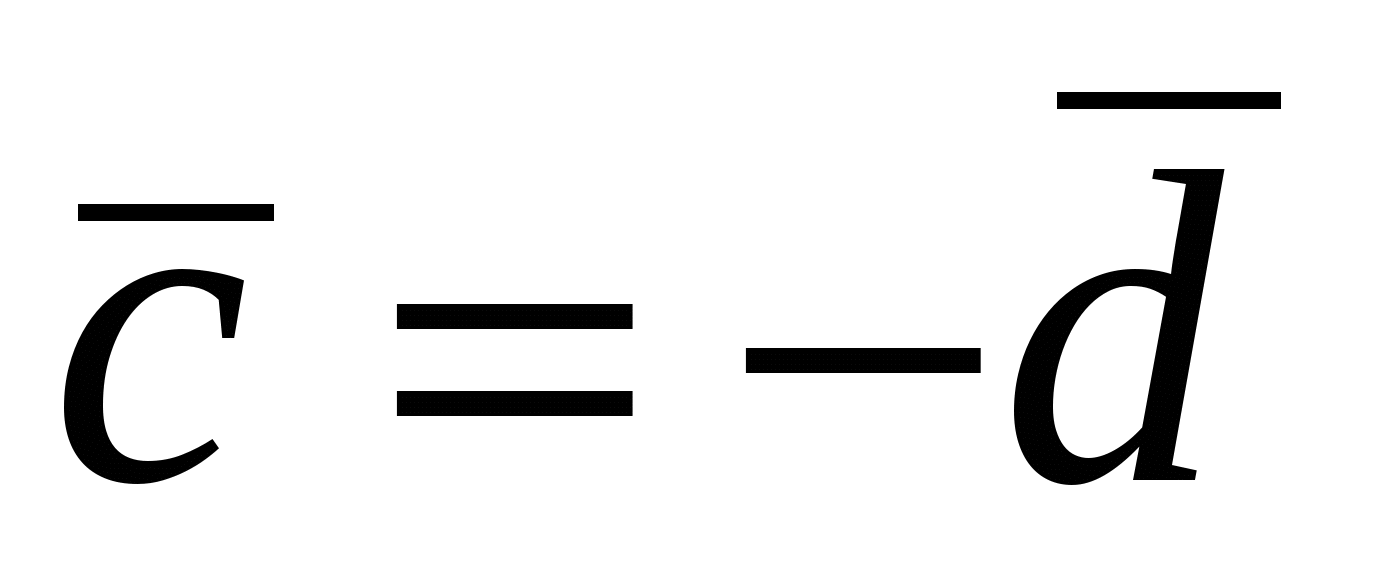 или или 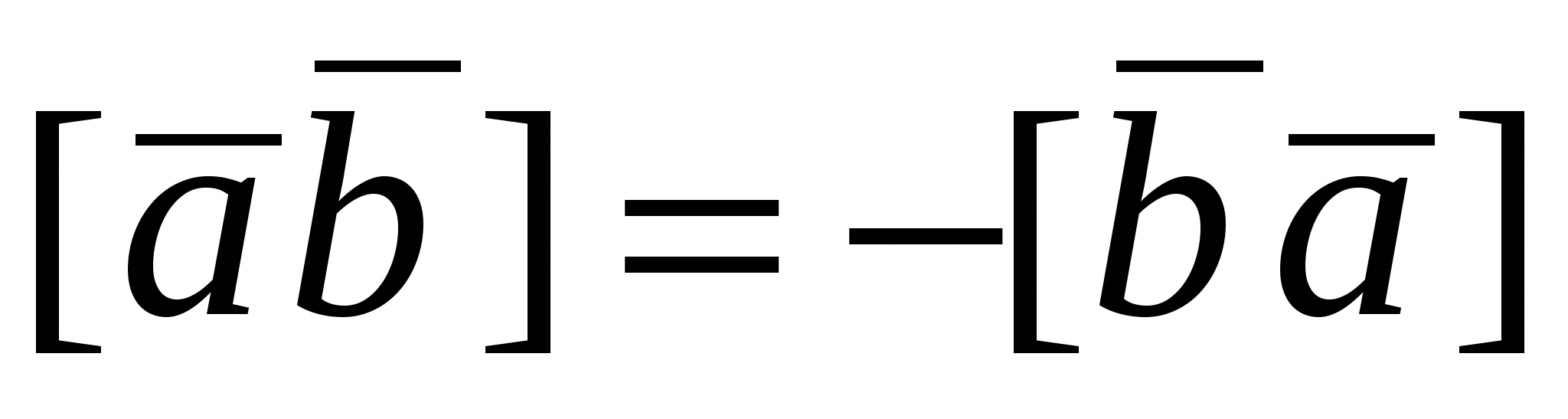 . .
 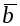 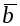
 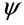 
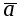 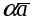 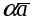 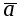
Рис. 16.
2. Пусть 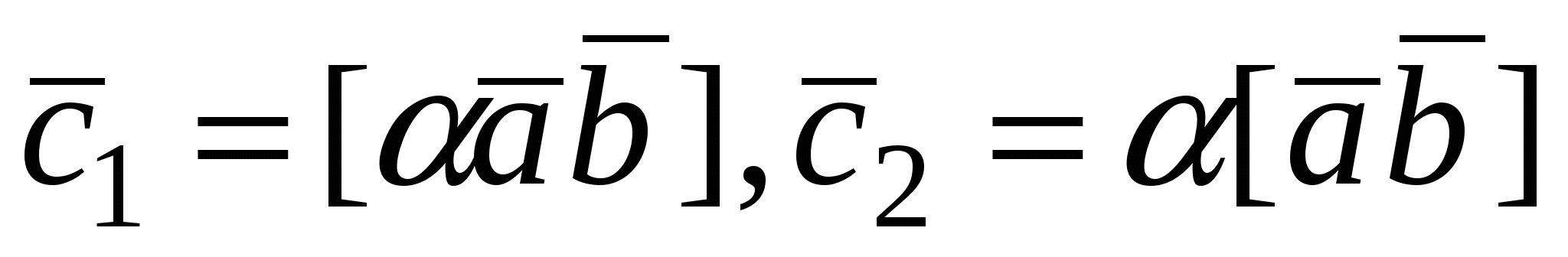 . По определению векторного произведения имеем . По определению векторного произведения имеем 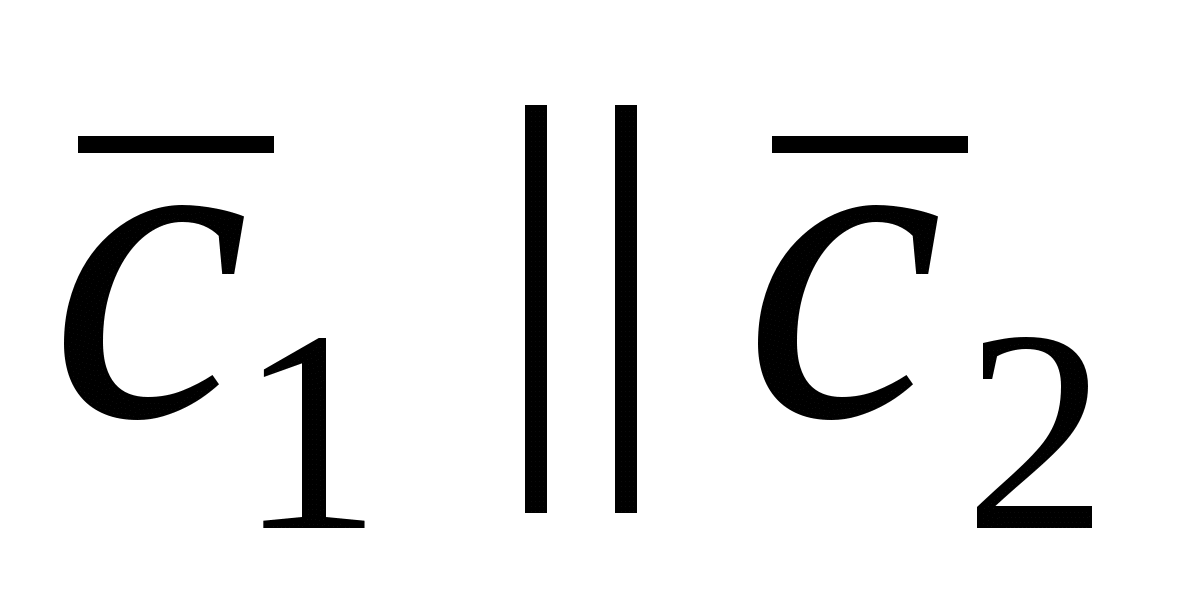 ; при ; при 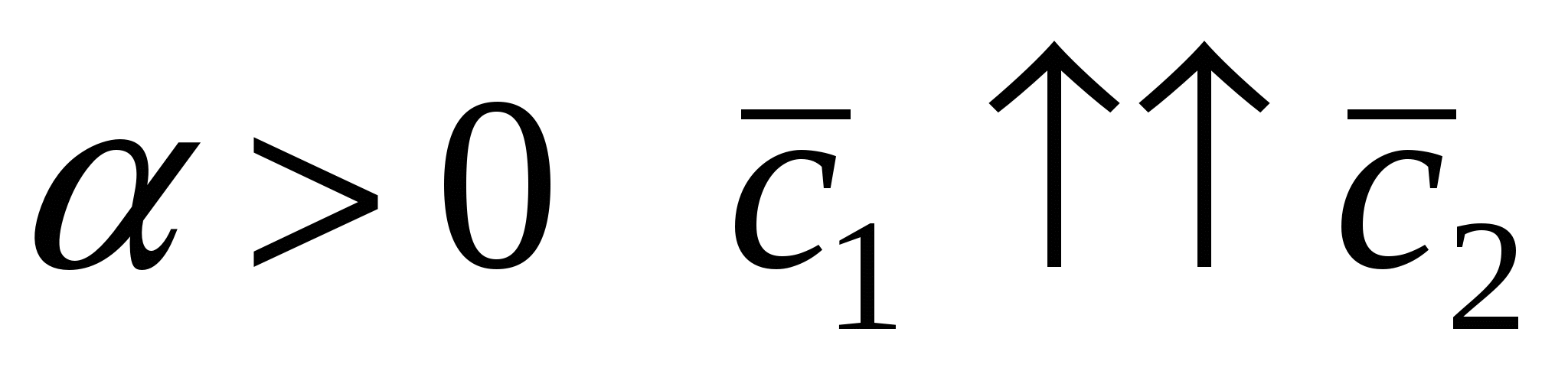 (рис.16), при (рис.16), при 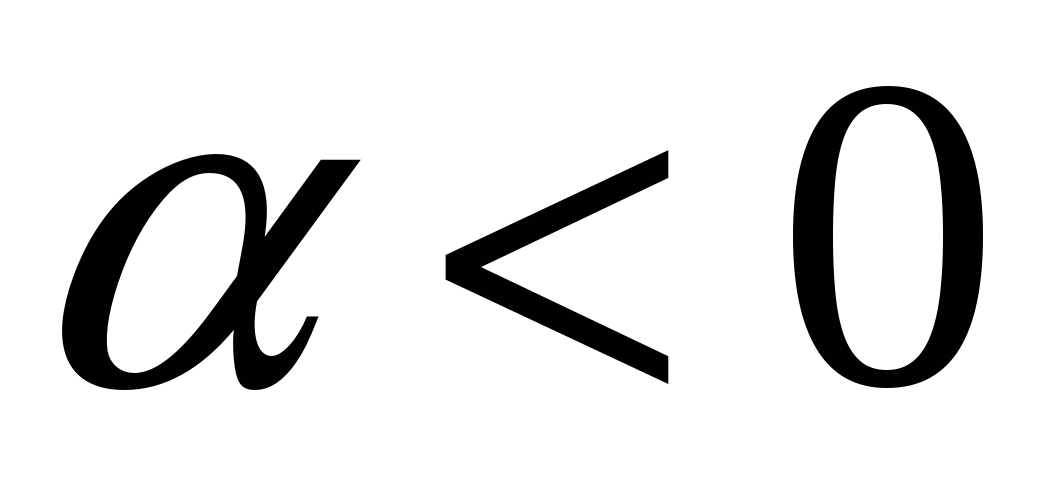 имеем имеем 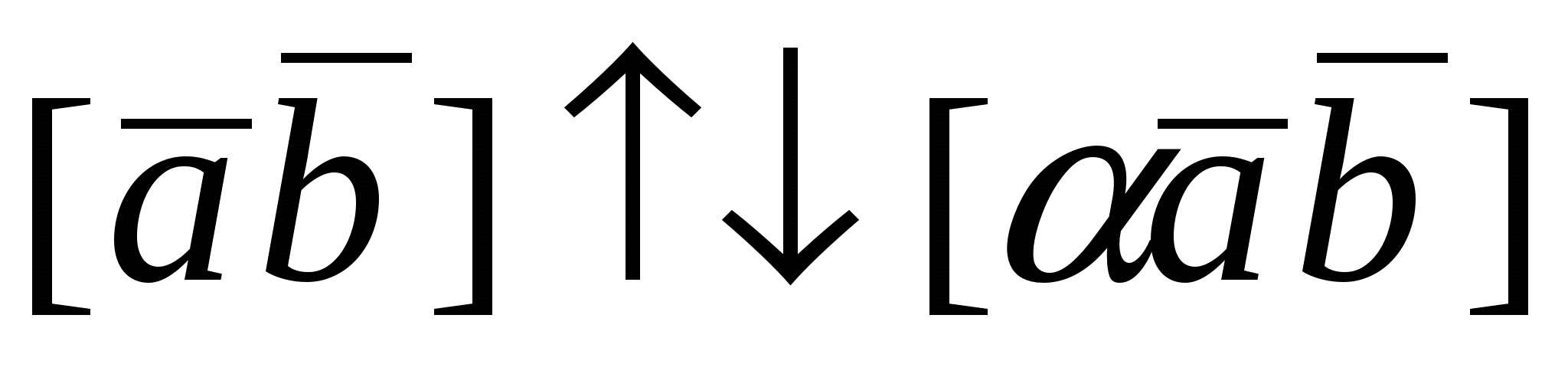 , откуда , откуда  , т.е. , т.е.  . Наконец, . Наконец, 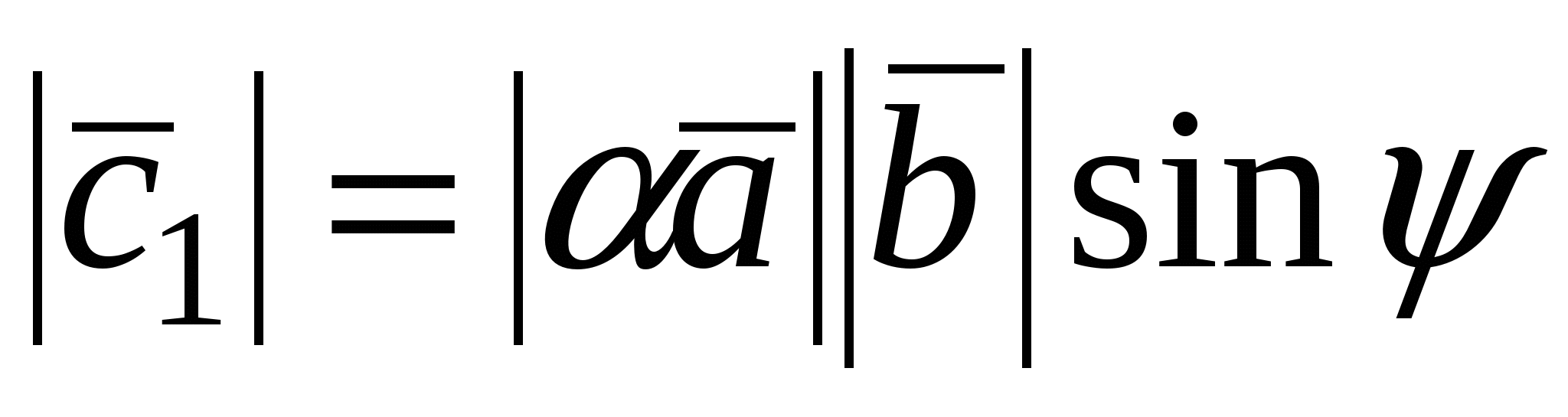 , где , где 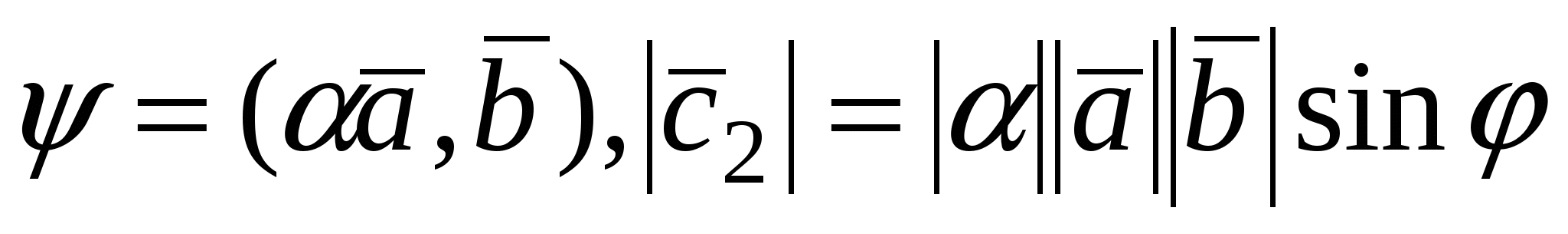 , ,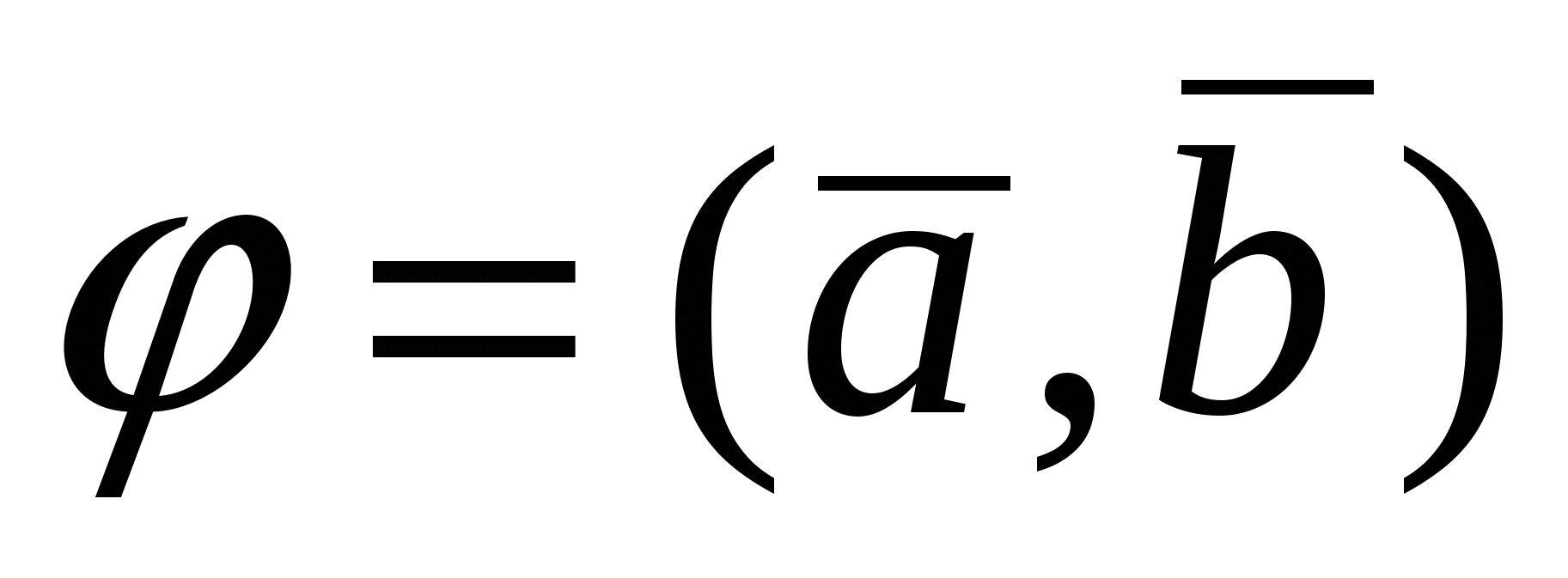 . Так как . Так как 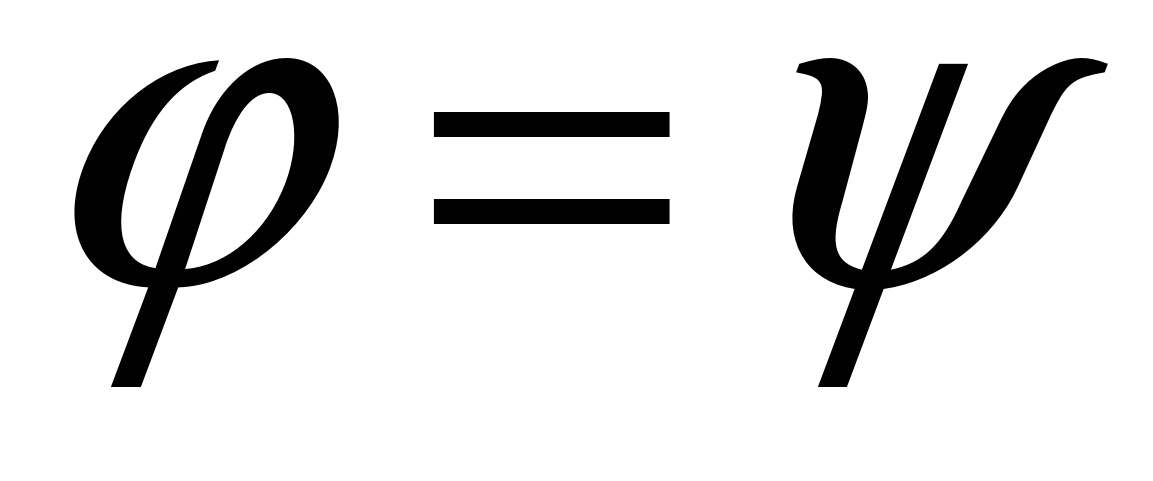 или или 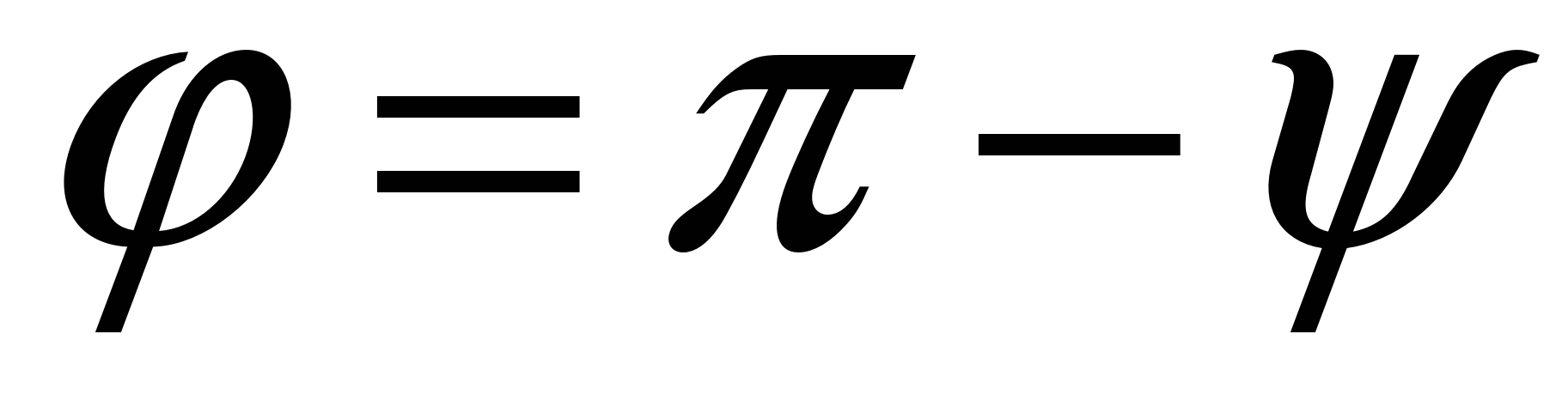 , то в любом случае , то в любом случае 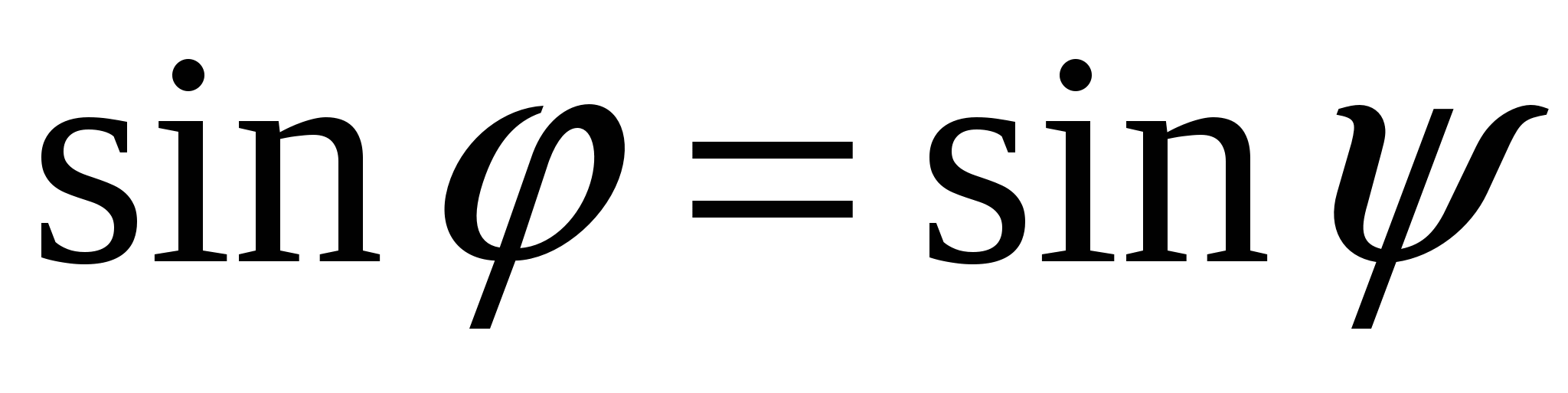 , следовательно, , следовательно, 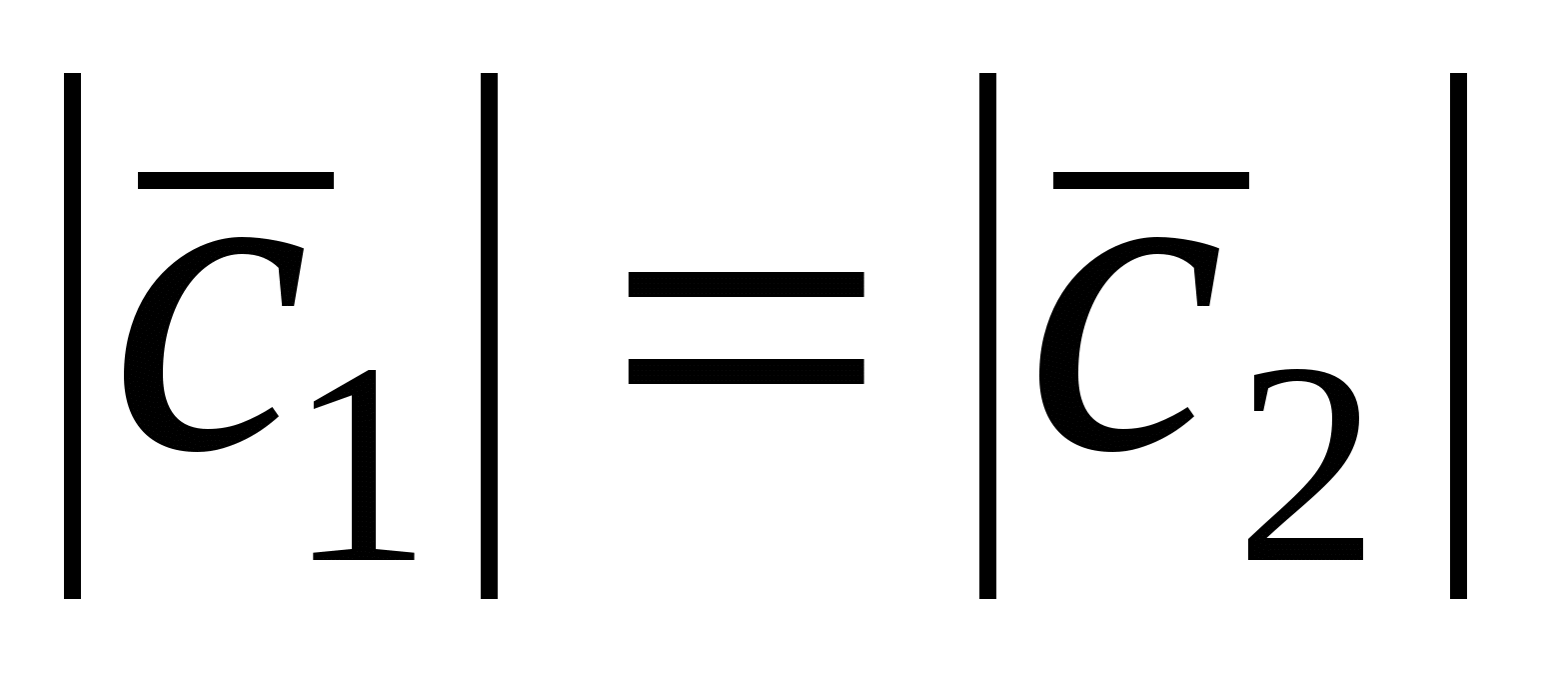 . Итак, получим, что . Итак, получим, что 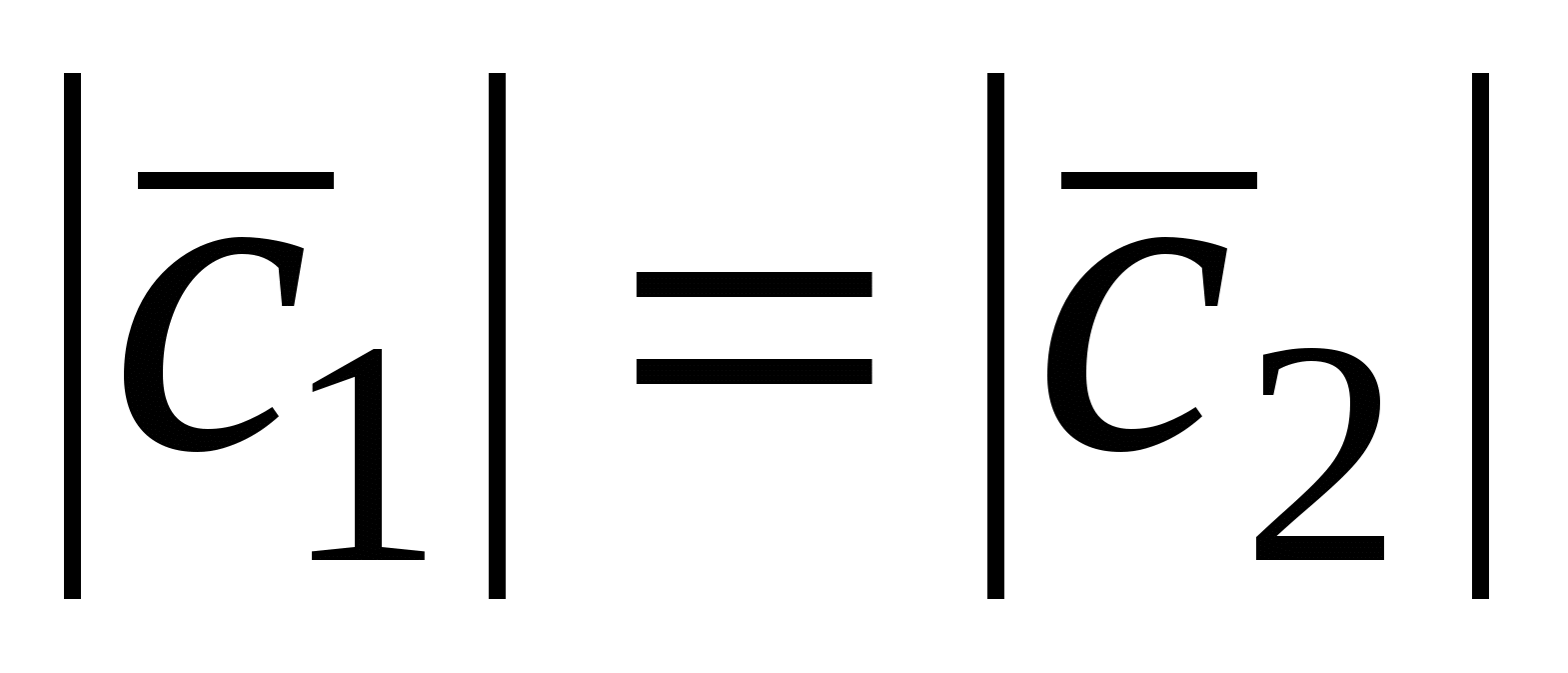 и и  , т. е. , т. е. 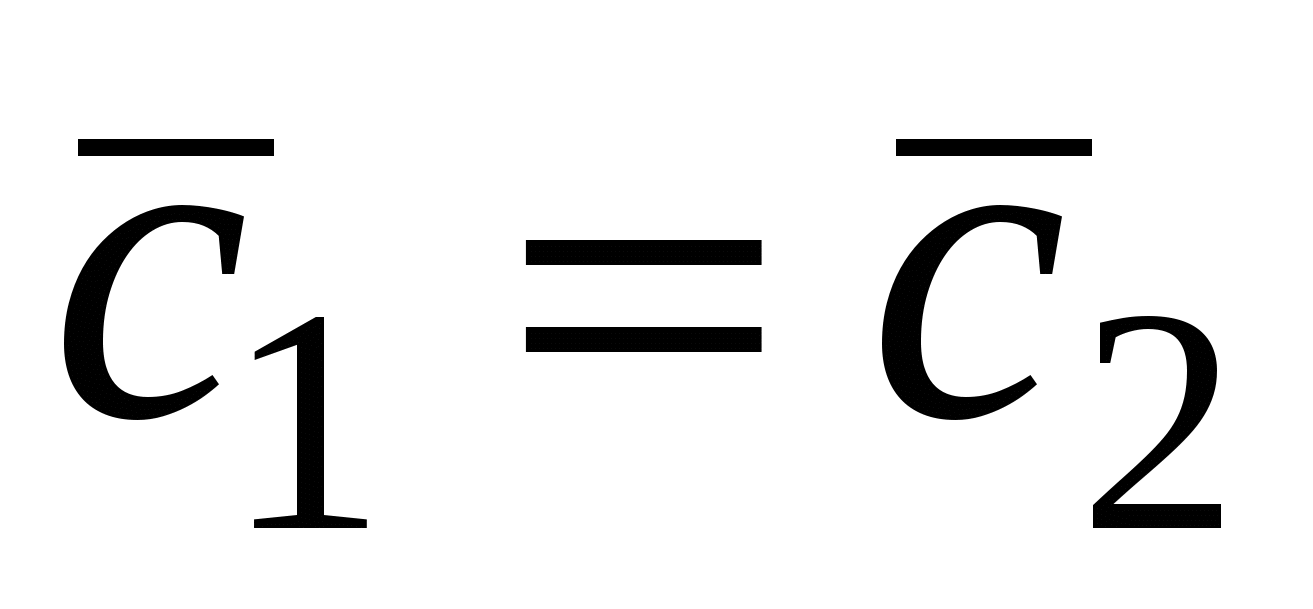 или или 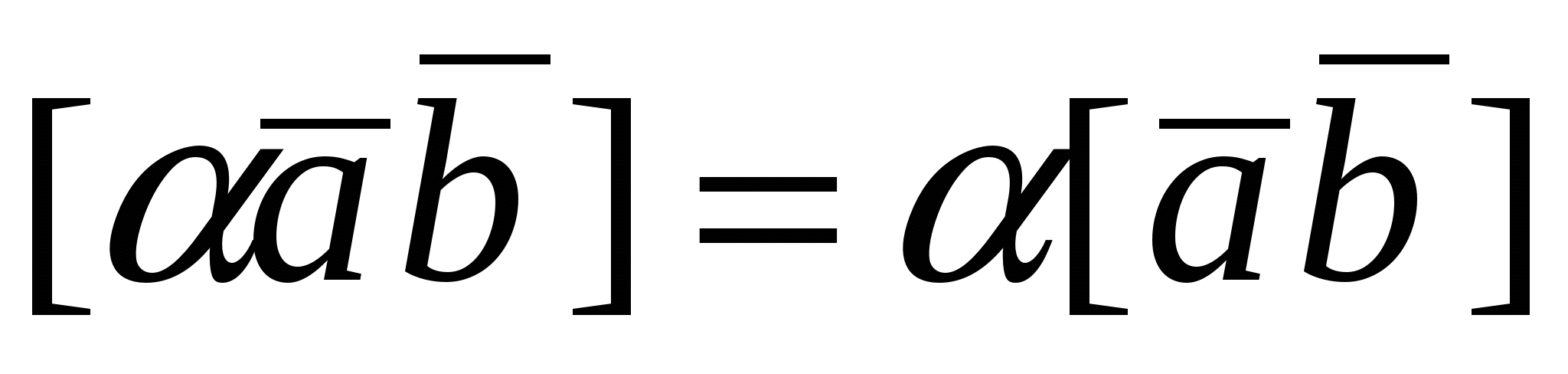 . .
ОРТОНОРМИРОВАННОГО БАЗИСА
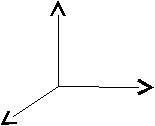 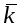
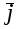
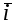
Рис. 17.
Рассмотрим векторы 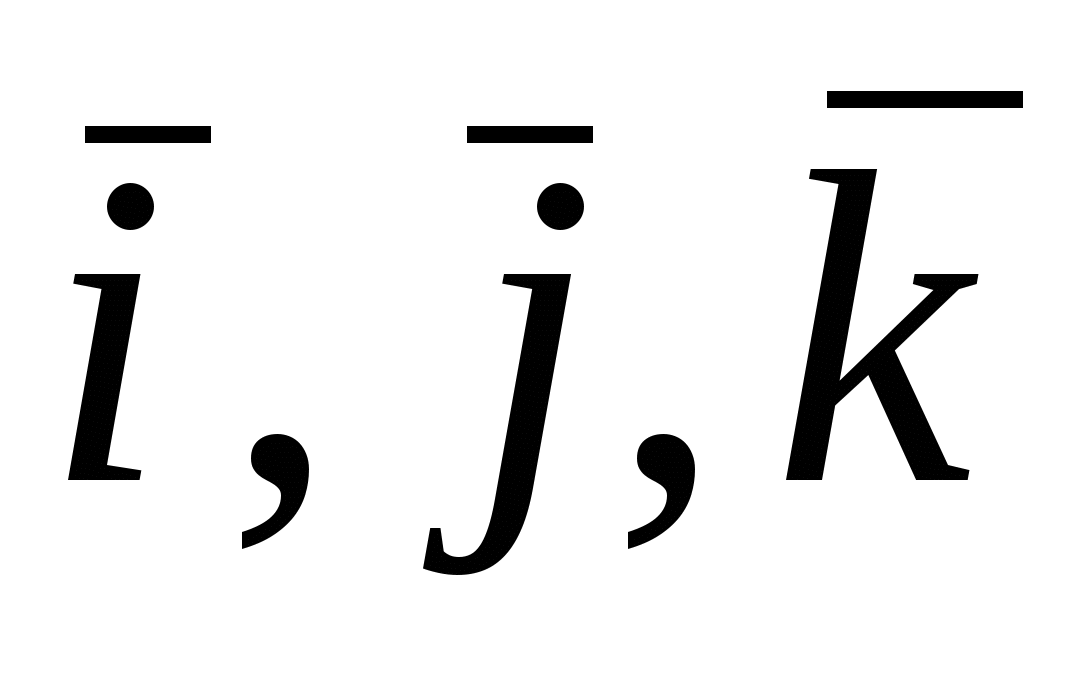 , которые образуют правую тройку ортонормированного базиса (рис.17). Рассмотрим вектор , которые образуют правую тройку ортонормированного базиса (рис.17). Рассмотрим вектор  . Этот вектор ортогонален к вектору . Этот вектор ортогонален к вектору 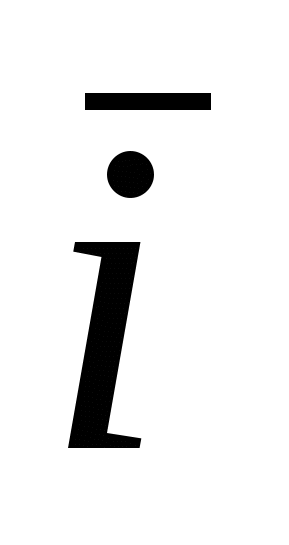 и вектору и вектору 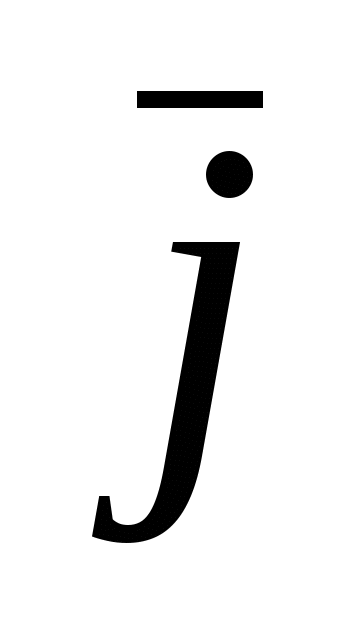 , следовательно, , следовательно,  , векторы , векторы 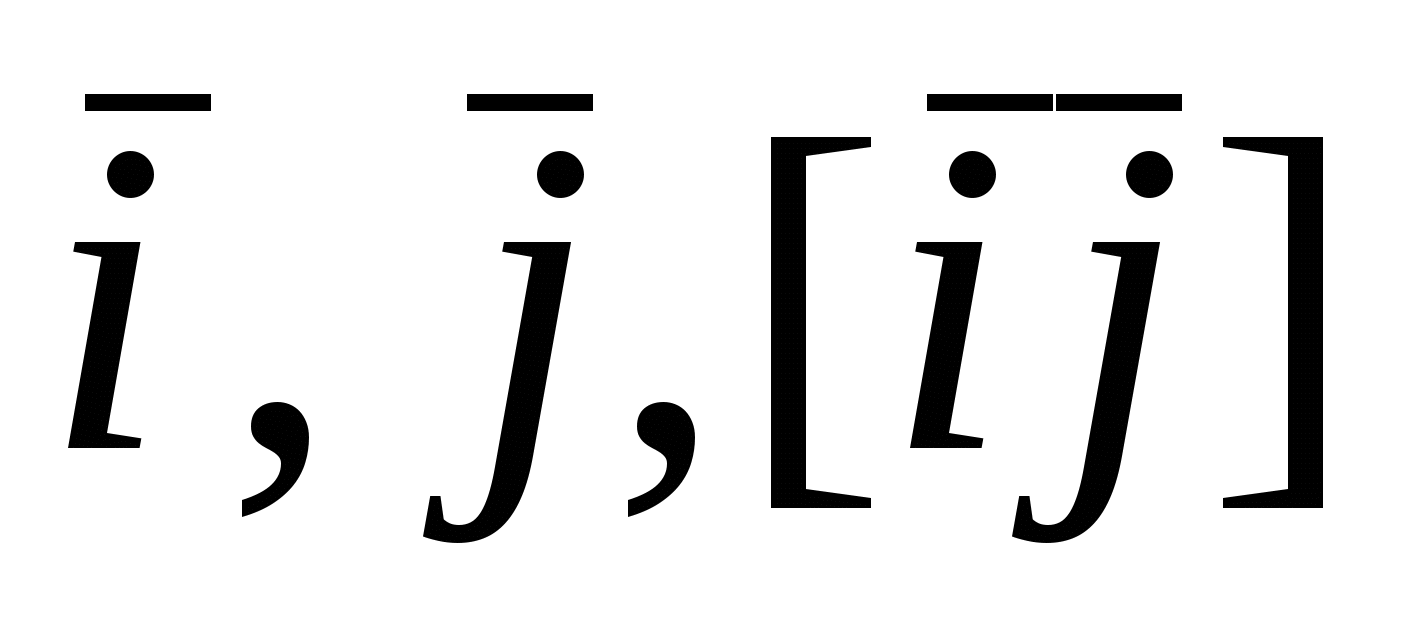 и и 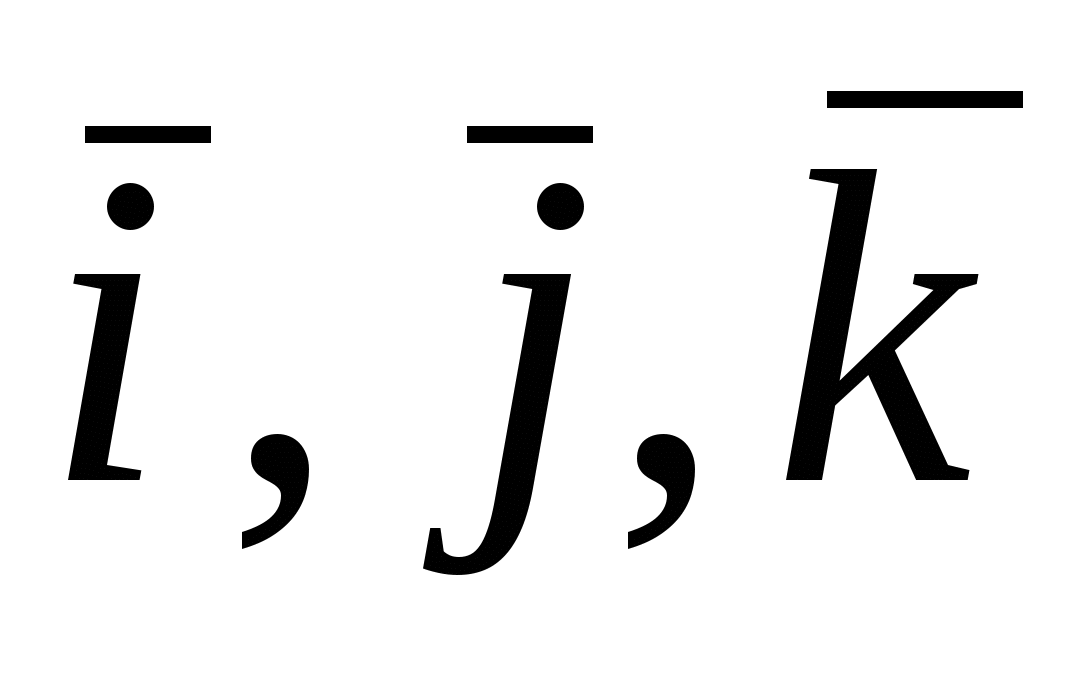 образуют правые тройки, следовательно, образуют правые тройки, следовательно, 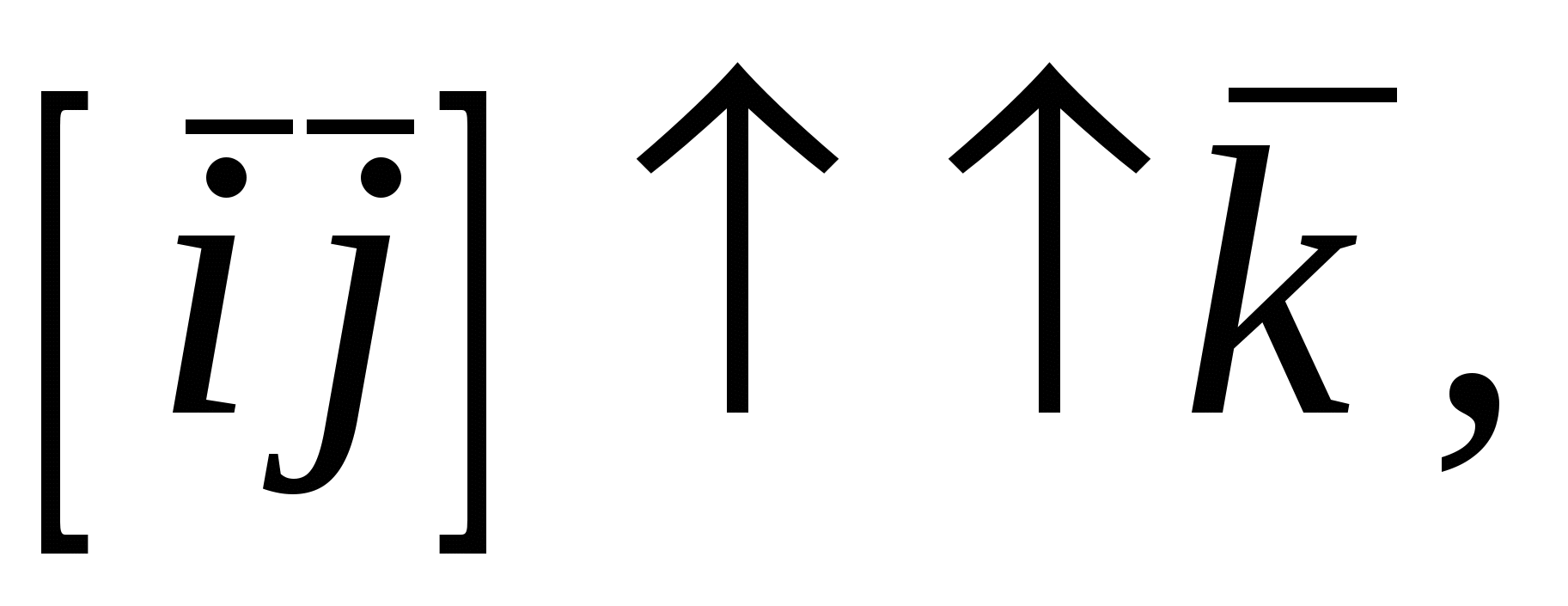 наконец, наконец,  . Итак . Итак 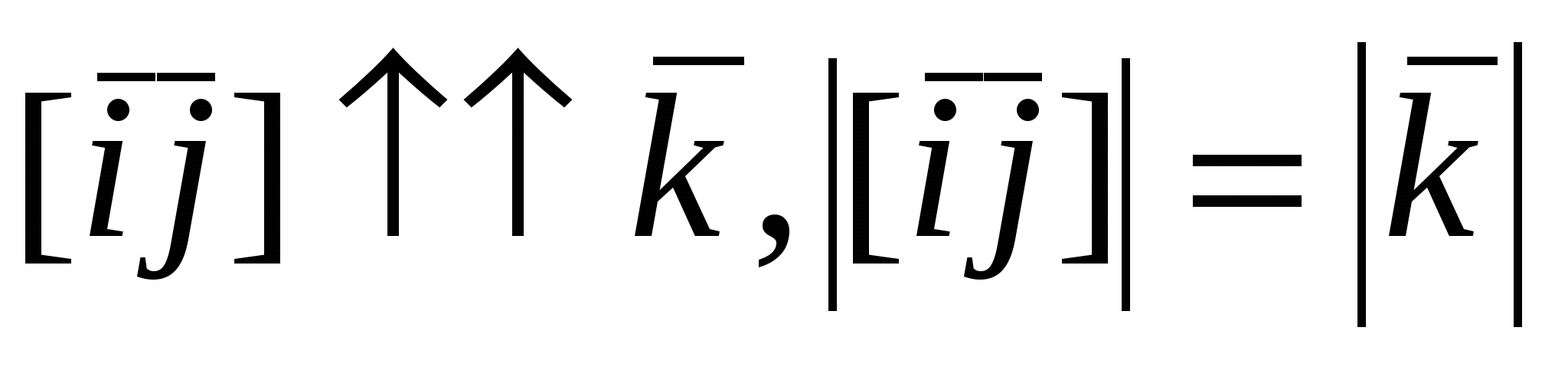 , откуда следует , откуда следует 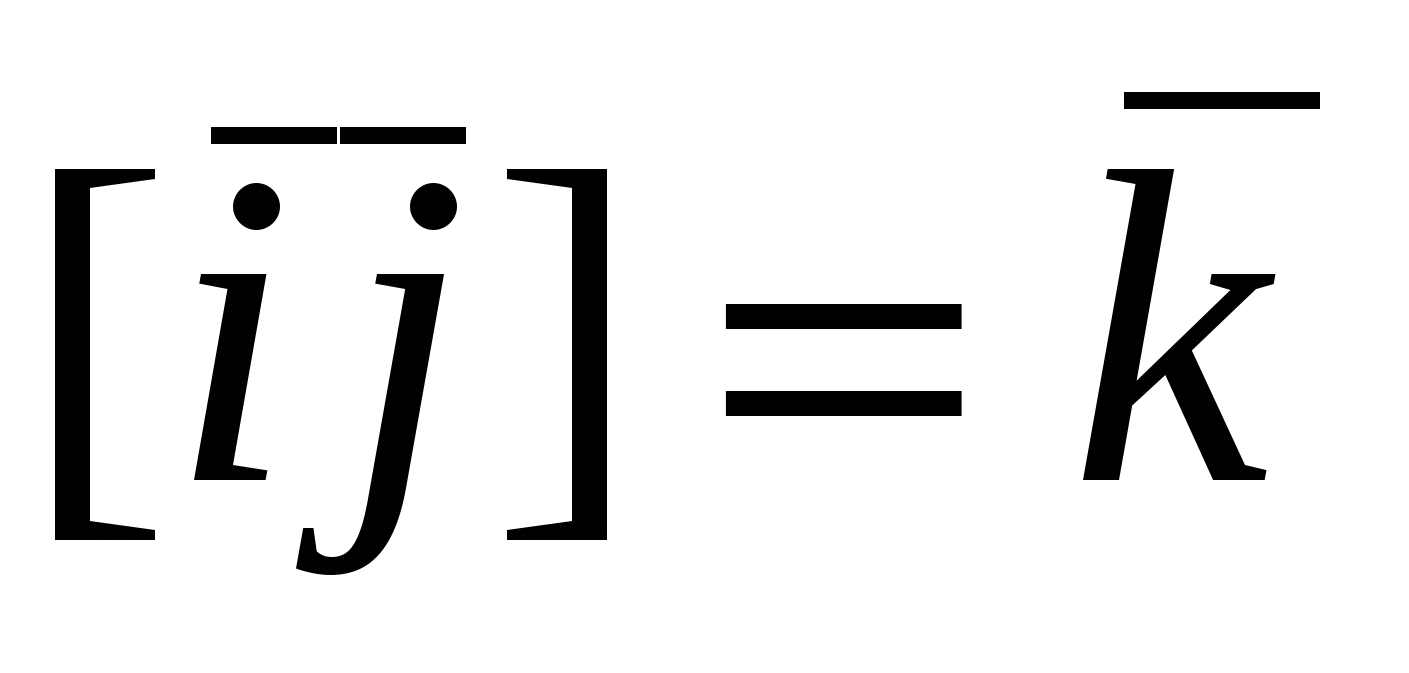 . Аналогично получим . Аналогично получим 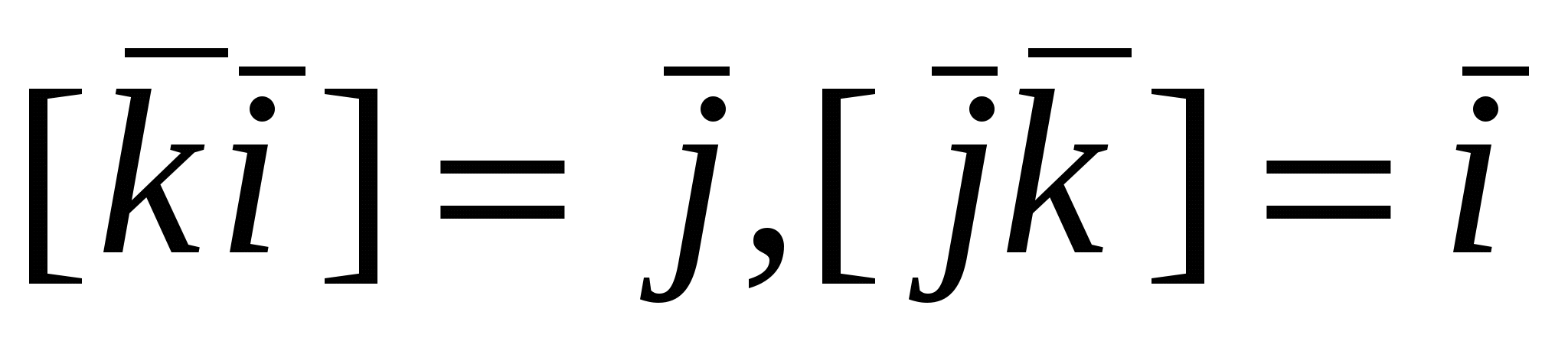 . .
Из свойства векторного произведения следует 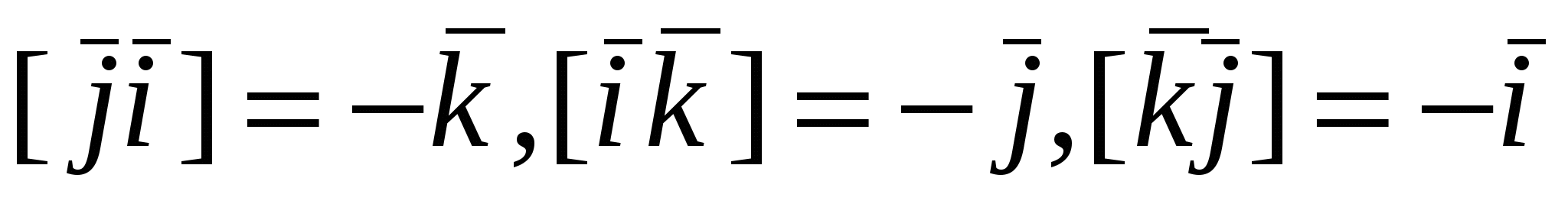 , а из определения - , а из определения - 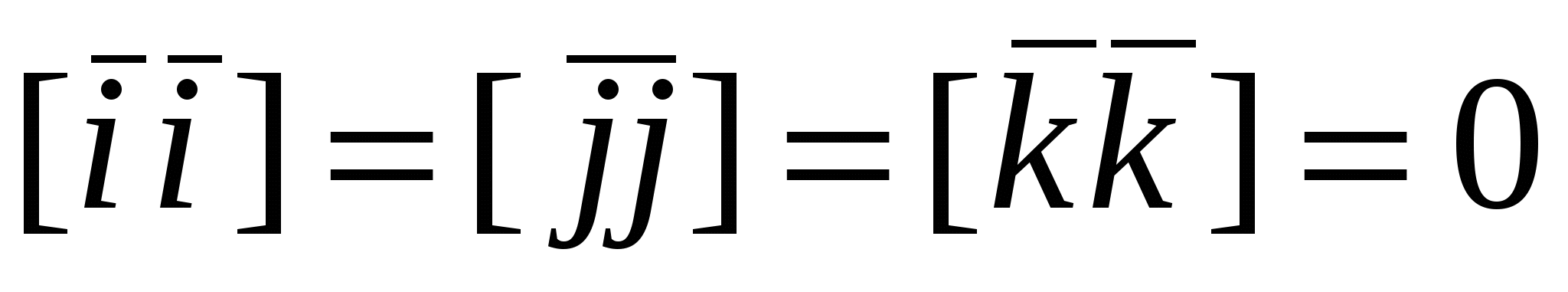 . .
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ В
ОРТОНОРМИРОВАННОМ БАЗИСЕ
Пусть 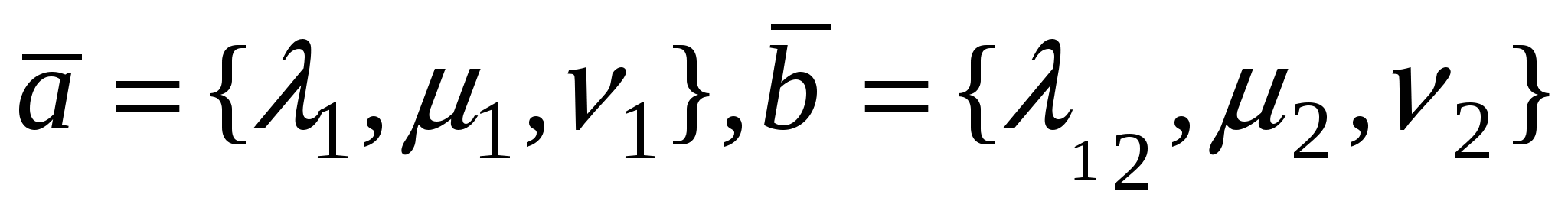 . Рассмотрим вектор . Рассмотрим вектор 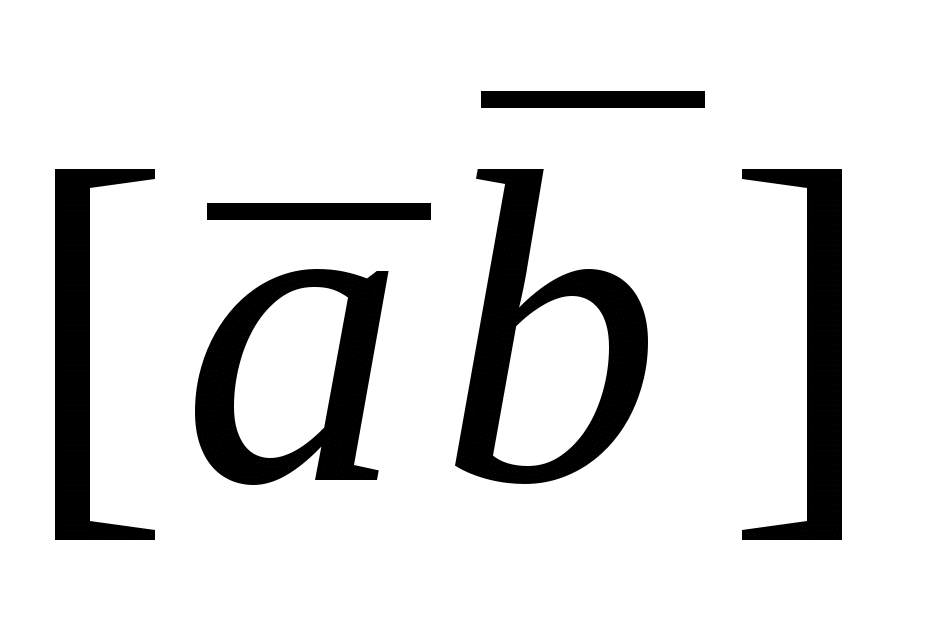 . Используя свойства векторного произведения, получим . Используя свойства векторного произведения, получим
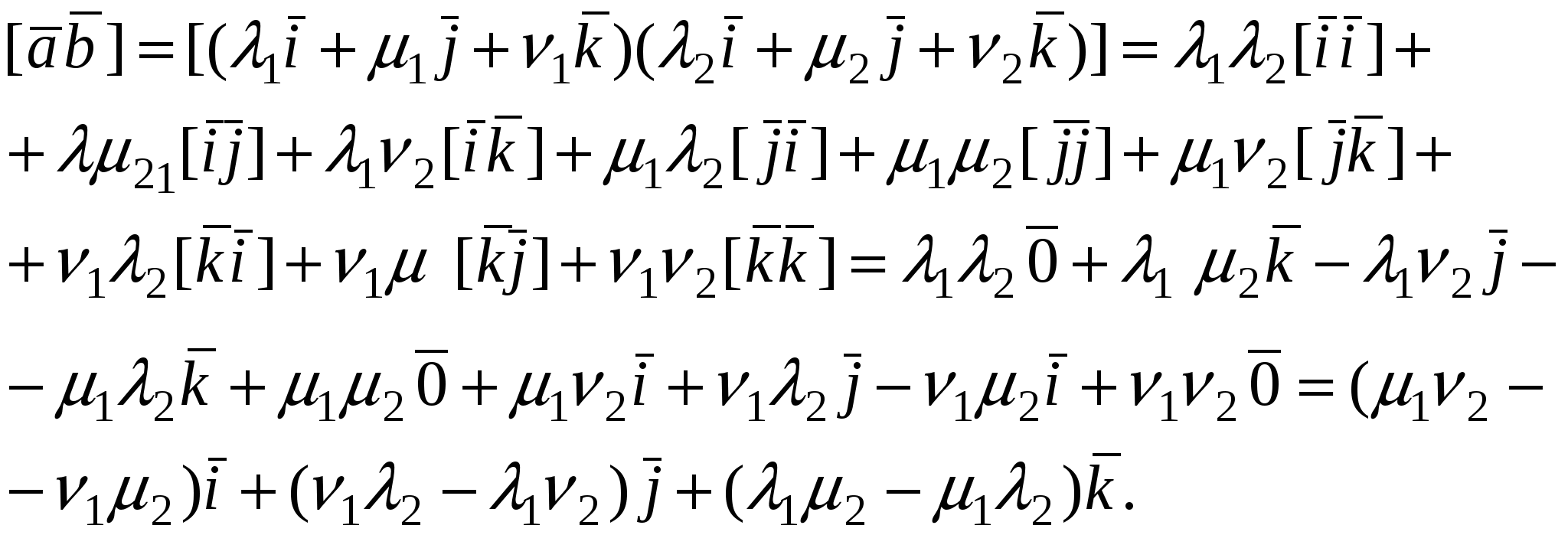
Следовательно, 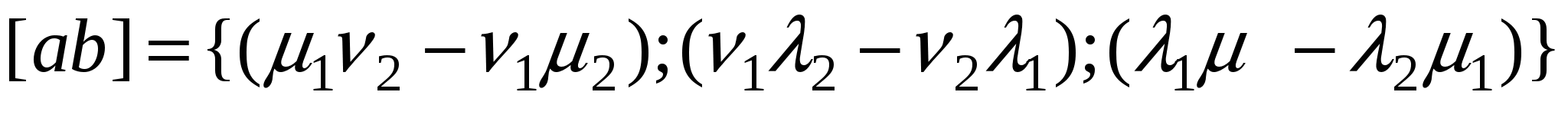 . .
Замечание. Для вычисления векторного произведения 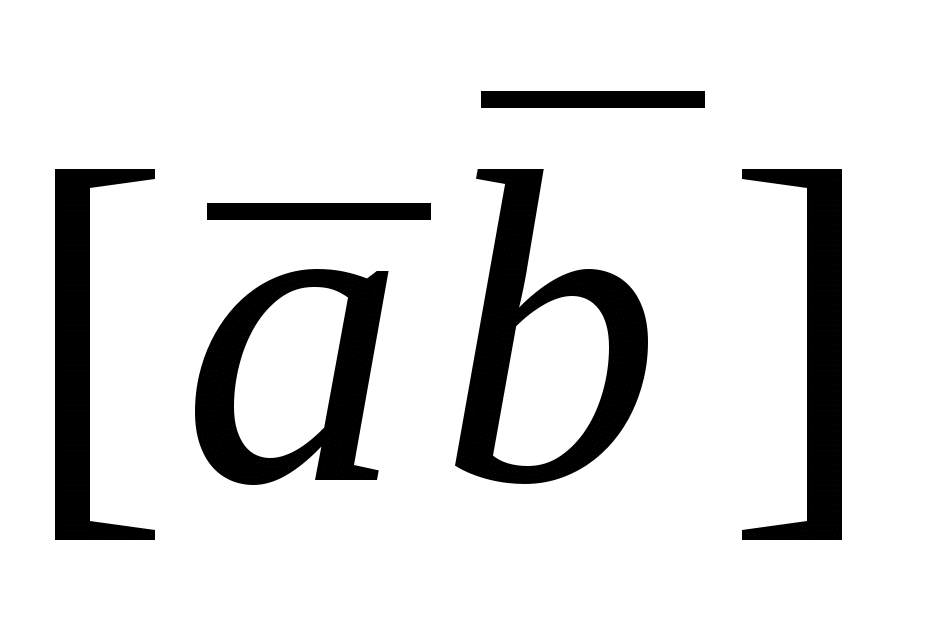 удобно использовать символ определителя: удобно использовать символ определителя:
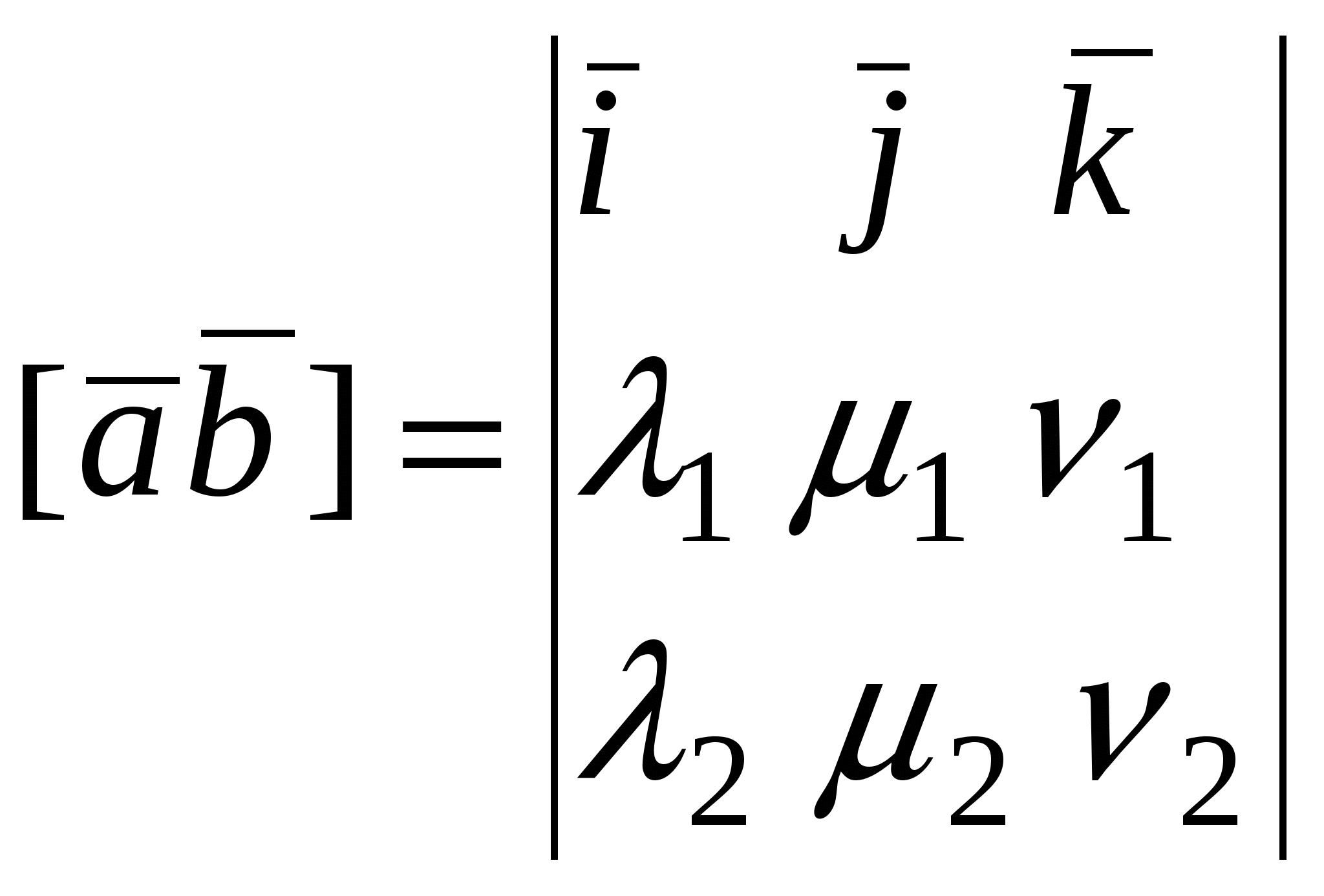 . .
Если этот определитель разложить по элементам первой строки, то получим разложение вектора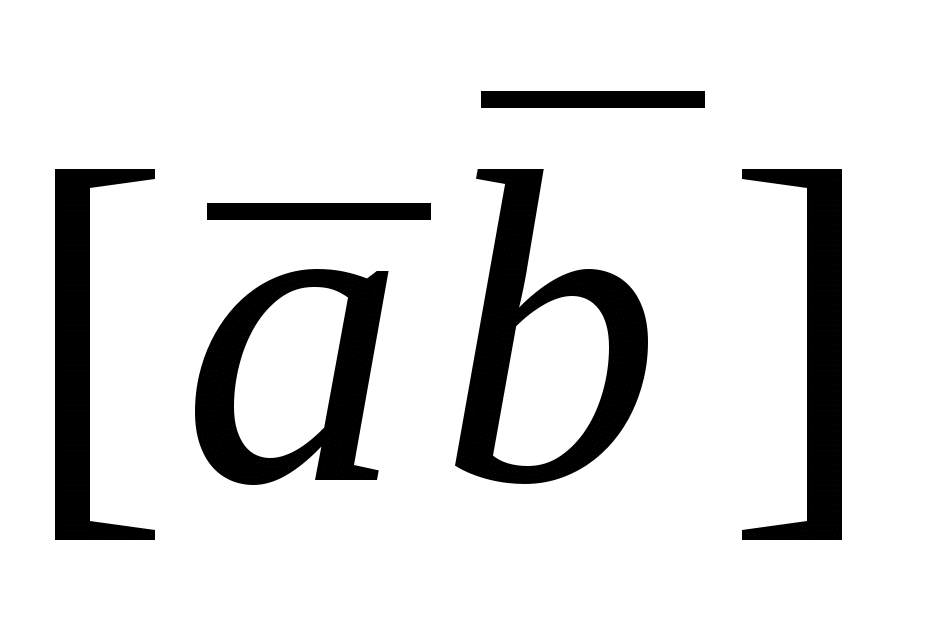 по направлениям базисных векторов: по направлениям базисных векторов:
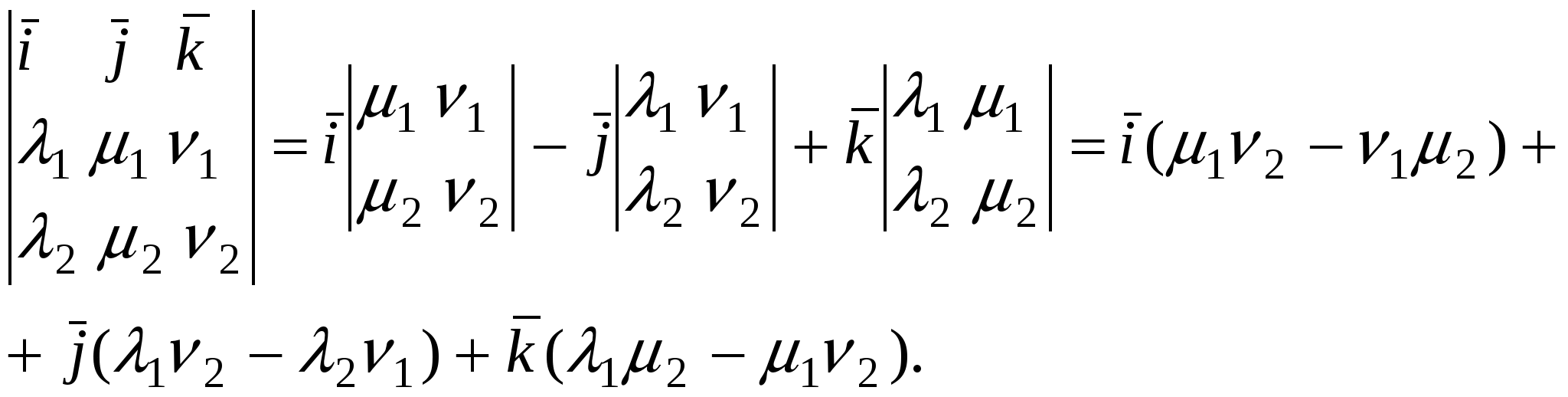
КОНТРОЛЬНЫЕ ВОПРОСЫ
Дайте определение векторного произведения.
Выведите формулу векторного произведения в ортонорми-рованном базисе.
§7. ВЕКТОРНО-СКАЛЯРНОЕ (СМЕШАННОЕ) ПРОИЗВЕДЕНИЕ
ТРЕХ ВЕКТОРОВ
Пусть даны три вектора 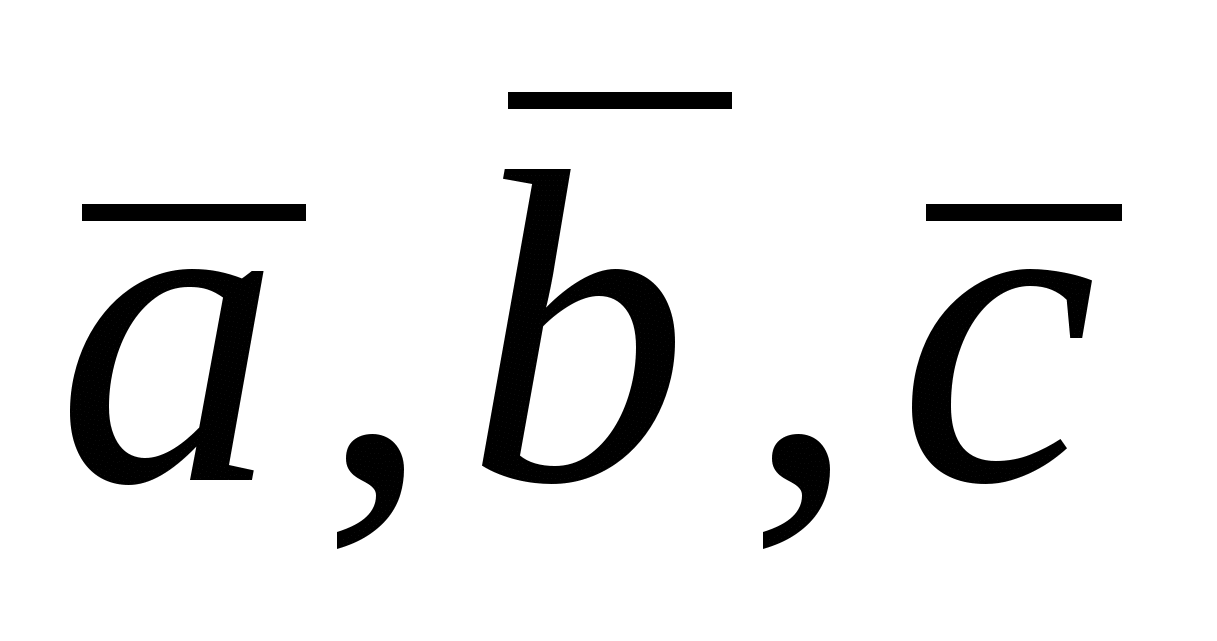 . Если вектор . Если вектор  умножается векторно на вектор умножается векторно на вектор 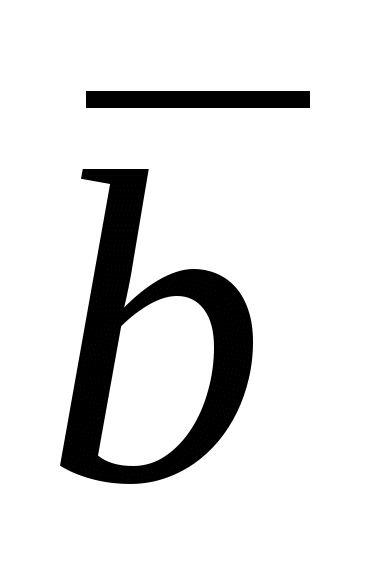 , а затем вектор , а затем вектор 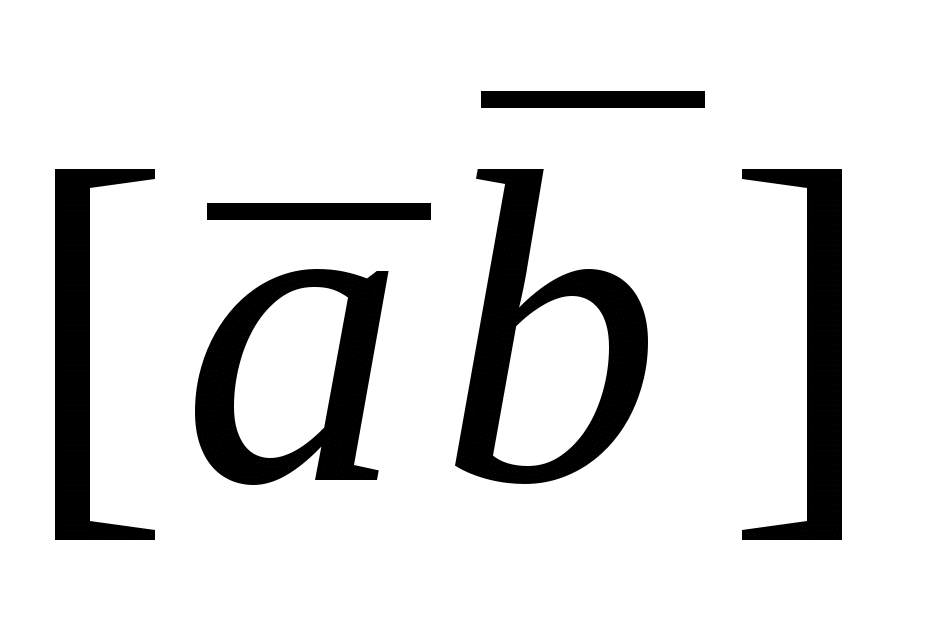 скалярно умножается на вектор скалярно умножается на вектор 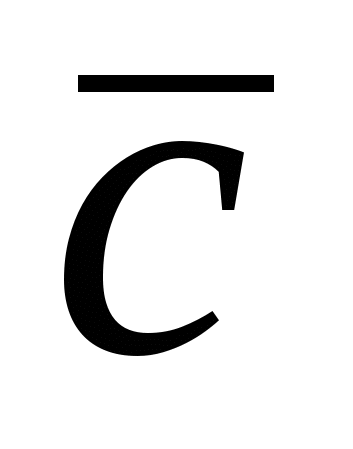 , то полученное число , то полученное число 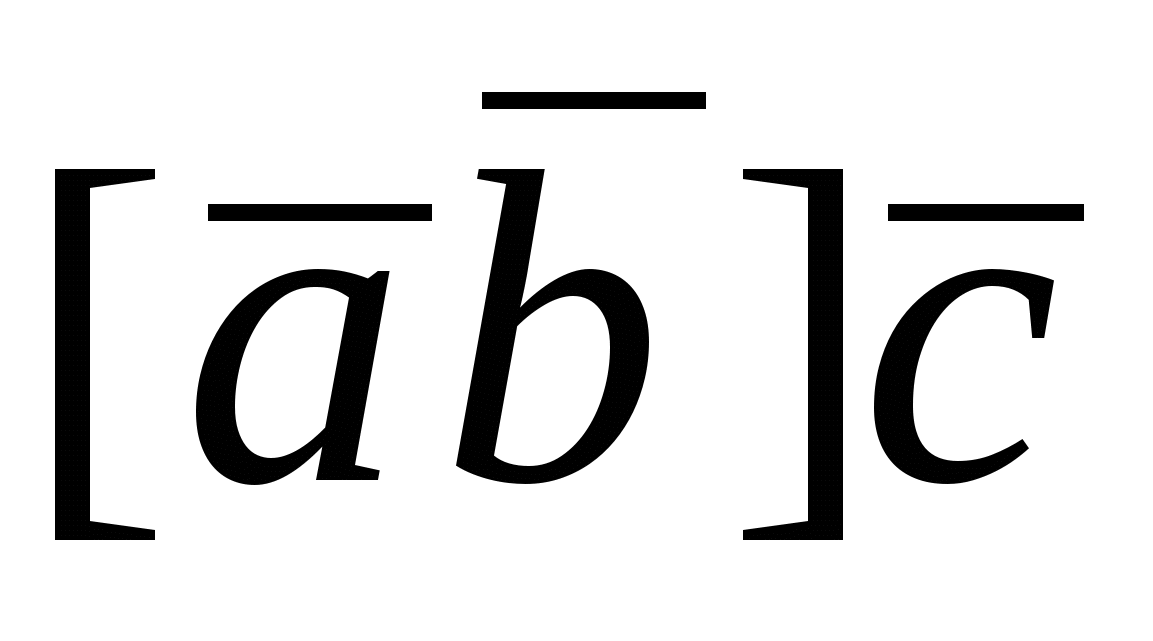 называется смешанным произведением векторов называется смешанным произведением векторов 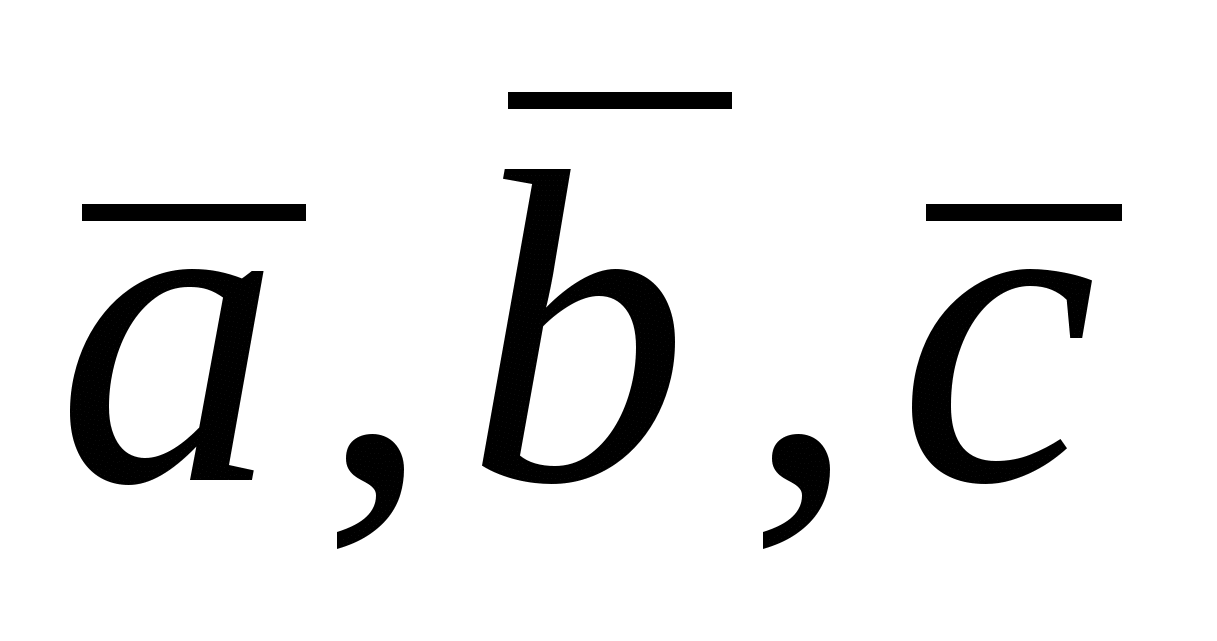 . .
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ СМЕШАННОГО ПРОИЗВЕДЕНИЯ
Рассмотрим смешанное произведение 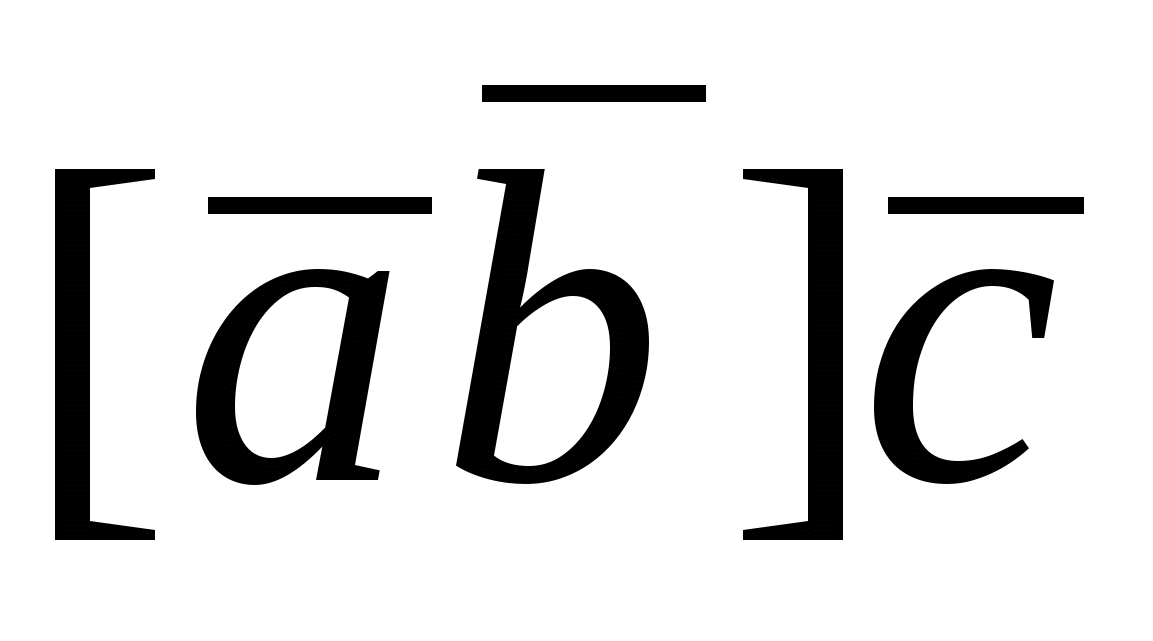 . Векторы . Векторы 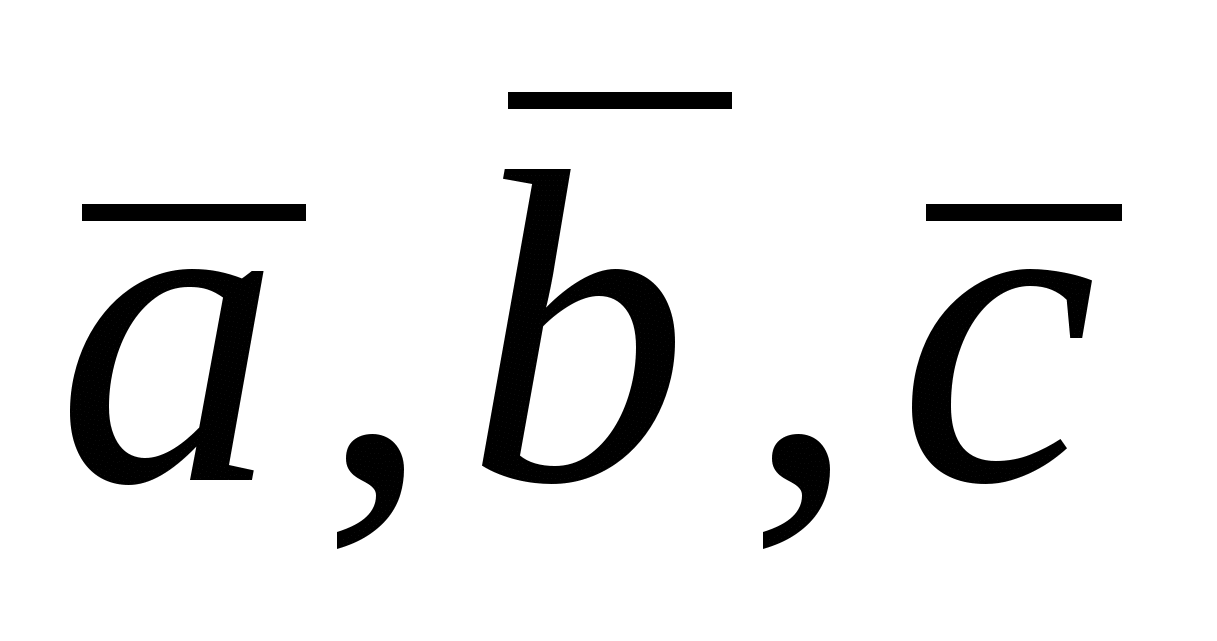 приведем к общему началу и построим на этих векторах параллелепипед (рис.18). приведем к общему началу и построим на этих векторах параллелепипед (рис.18).
Вектор 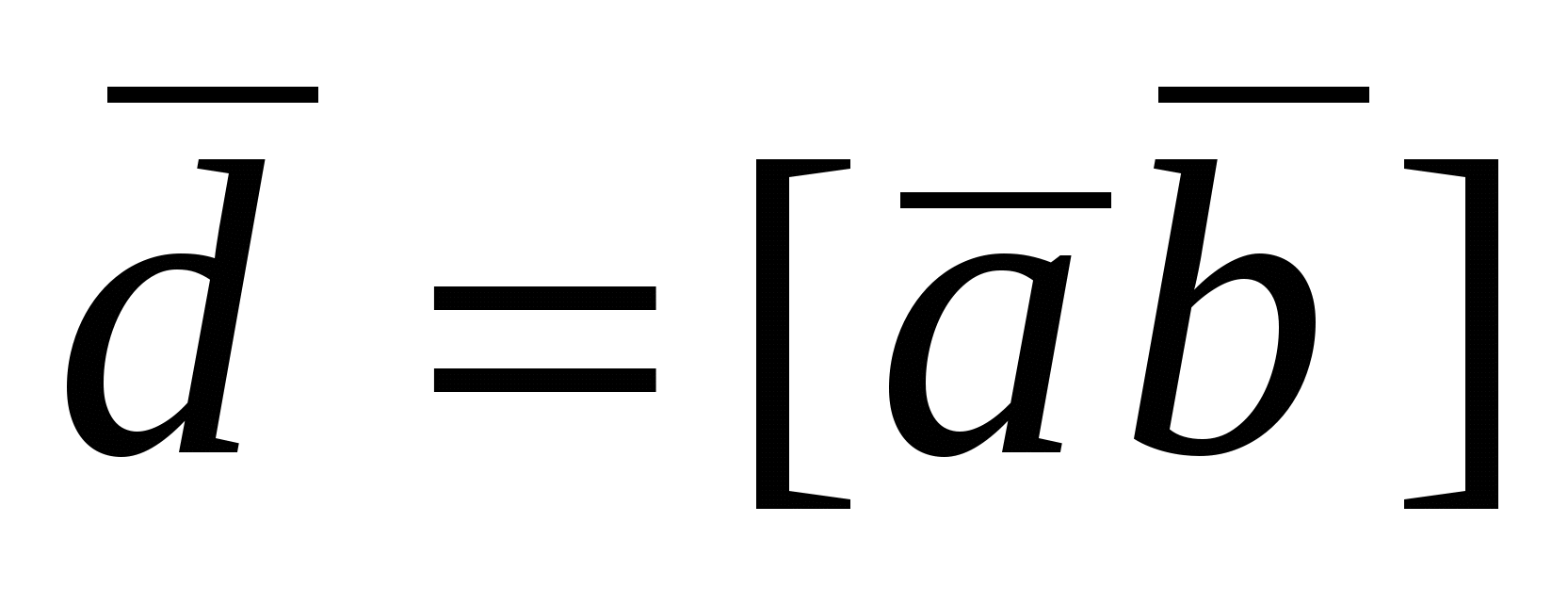 перпен-дикулярен основанию параллелепипеда и перпен-дикулярен основанию параллелепипеда и 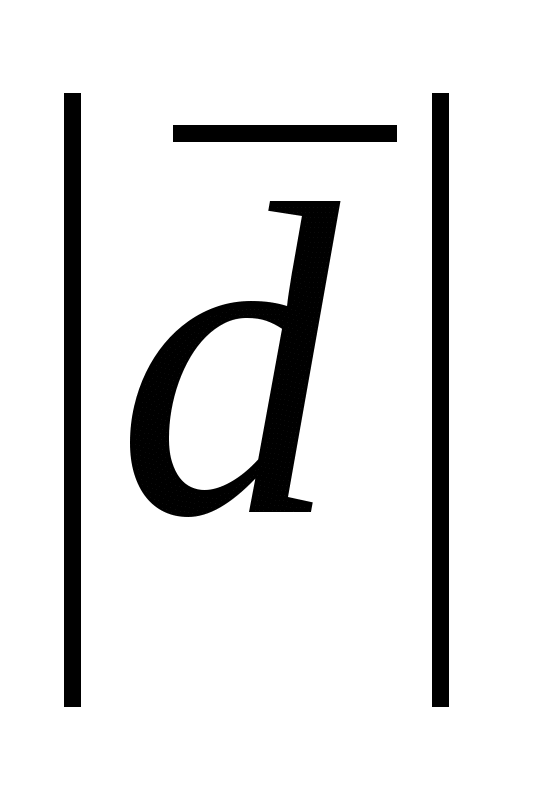 чис-ленно равен площади этого основания. чис-ленно равен площади этого основания.
По определению скалярное произведение 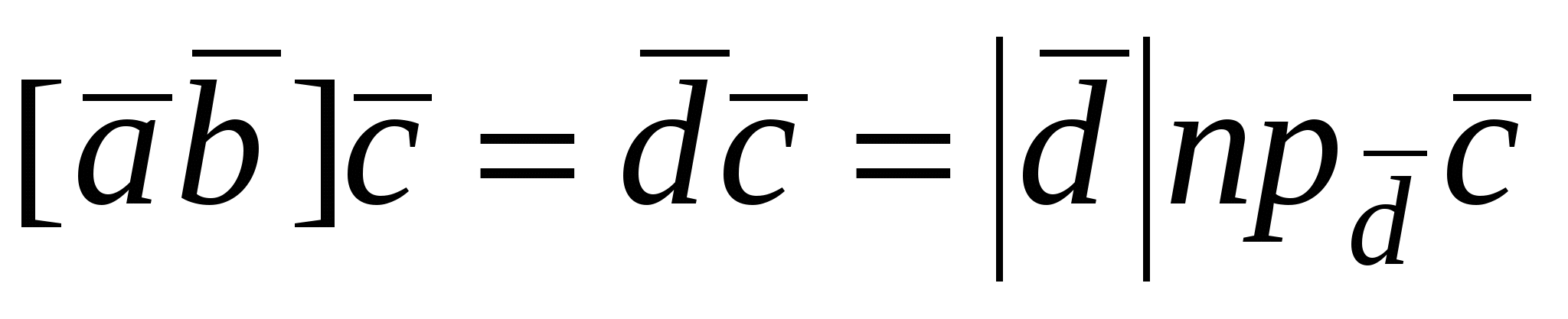 , но , но 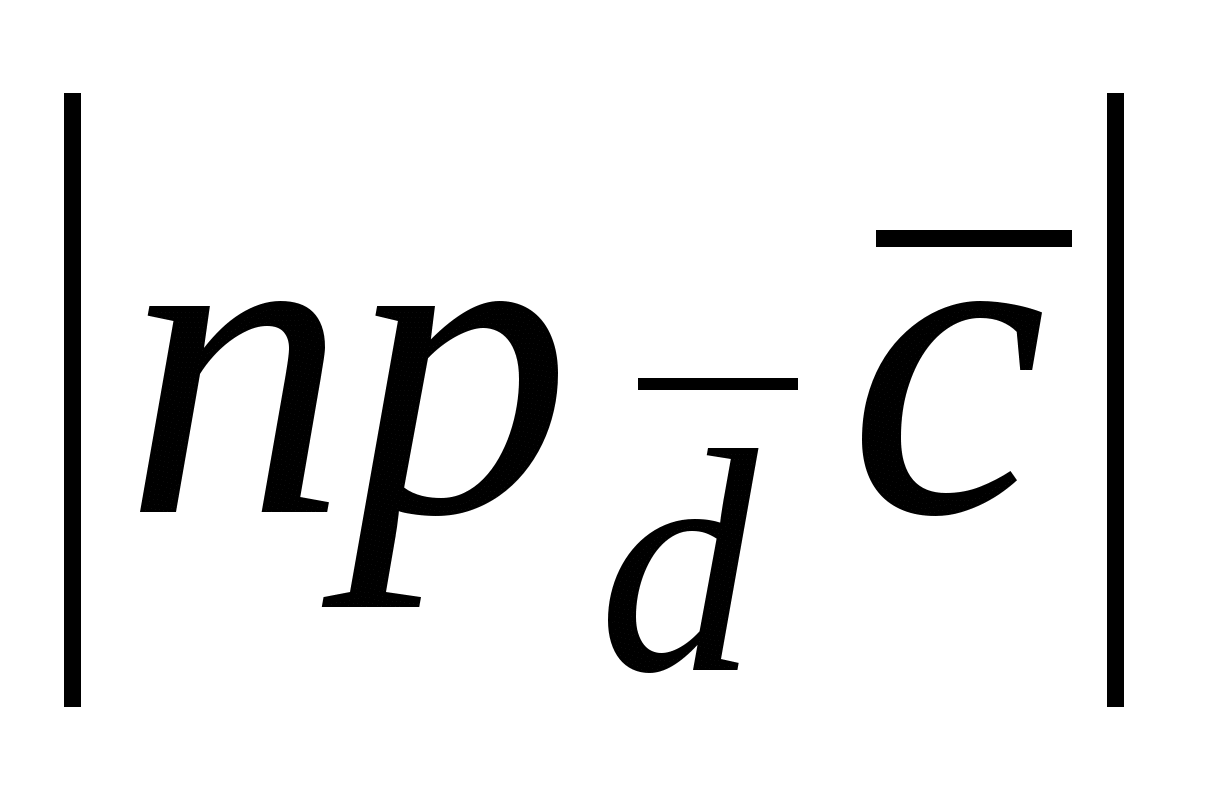 равна высоте равна высоте
|
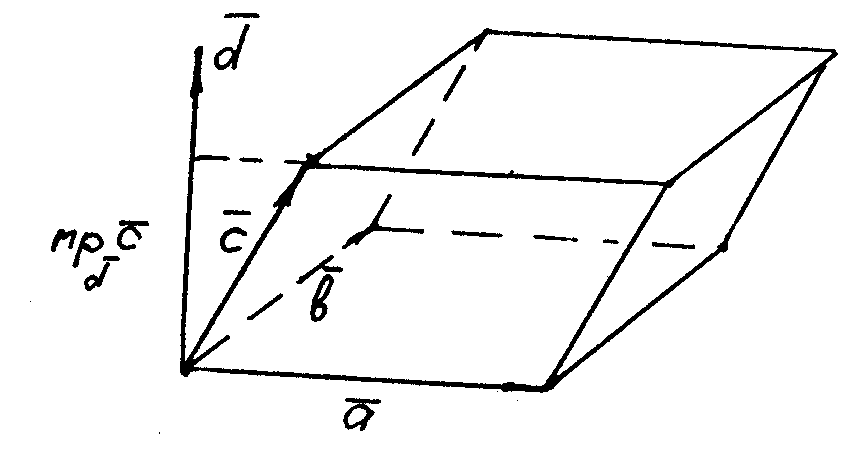
Рис. 18 |
параллелепипеда (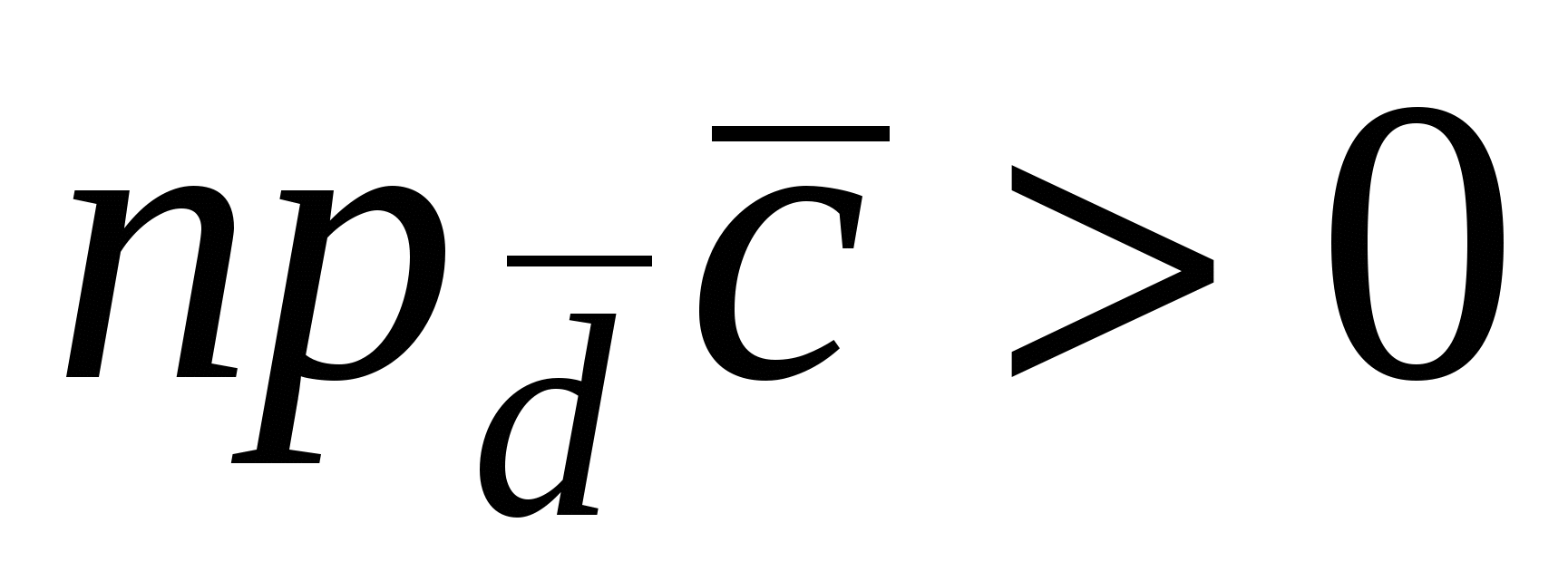 , если , если 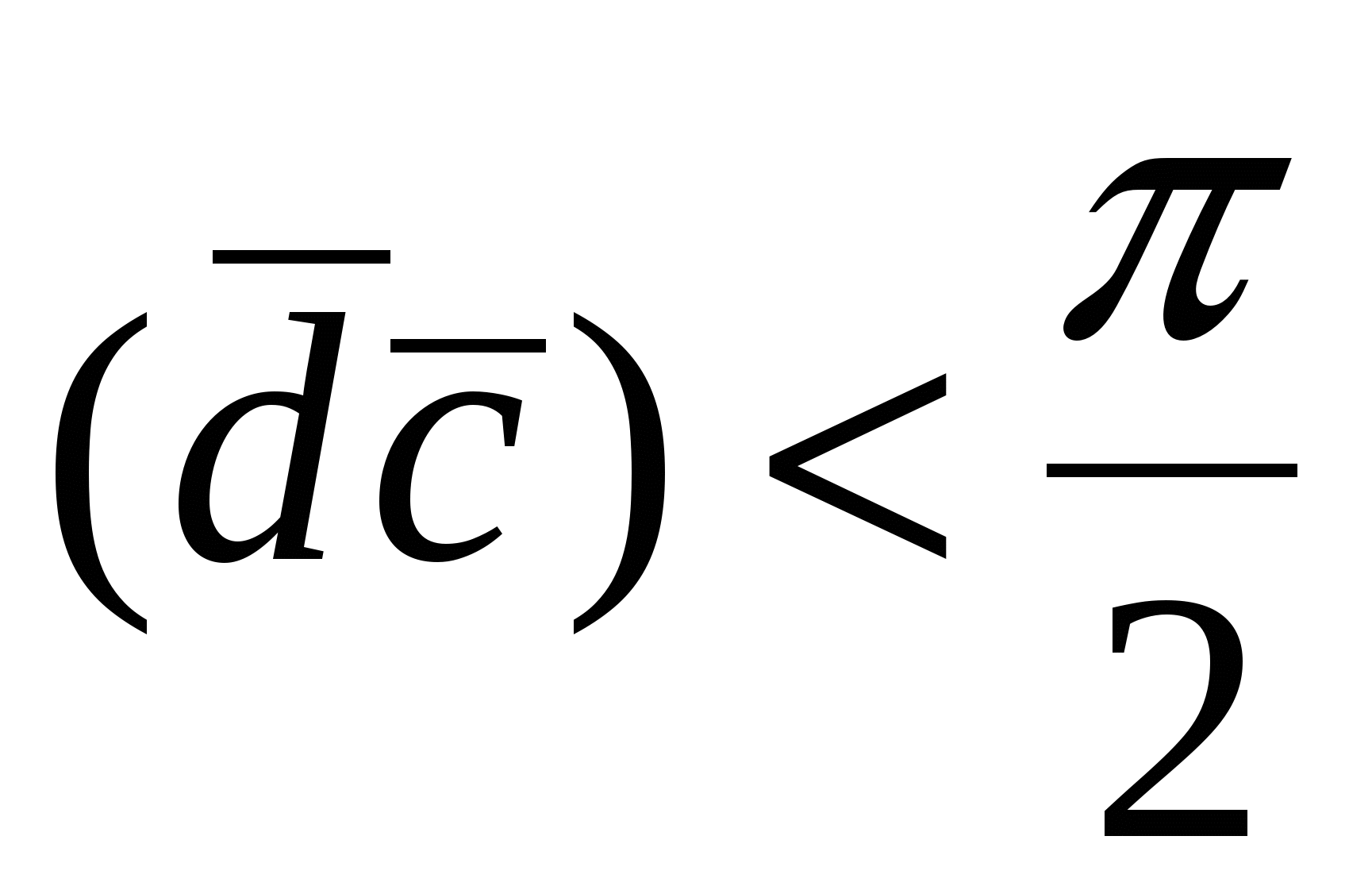 и и 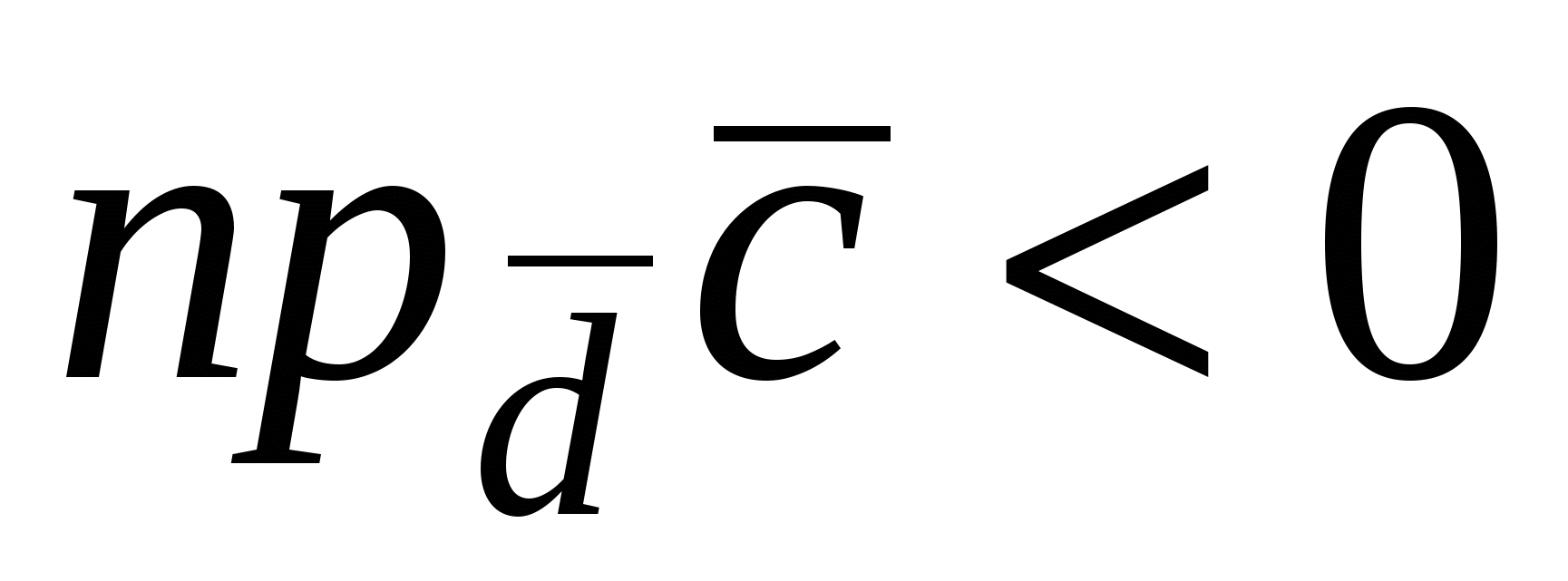 , если , если 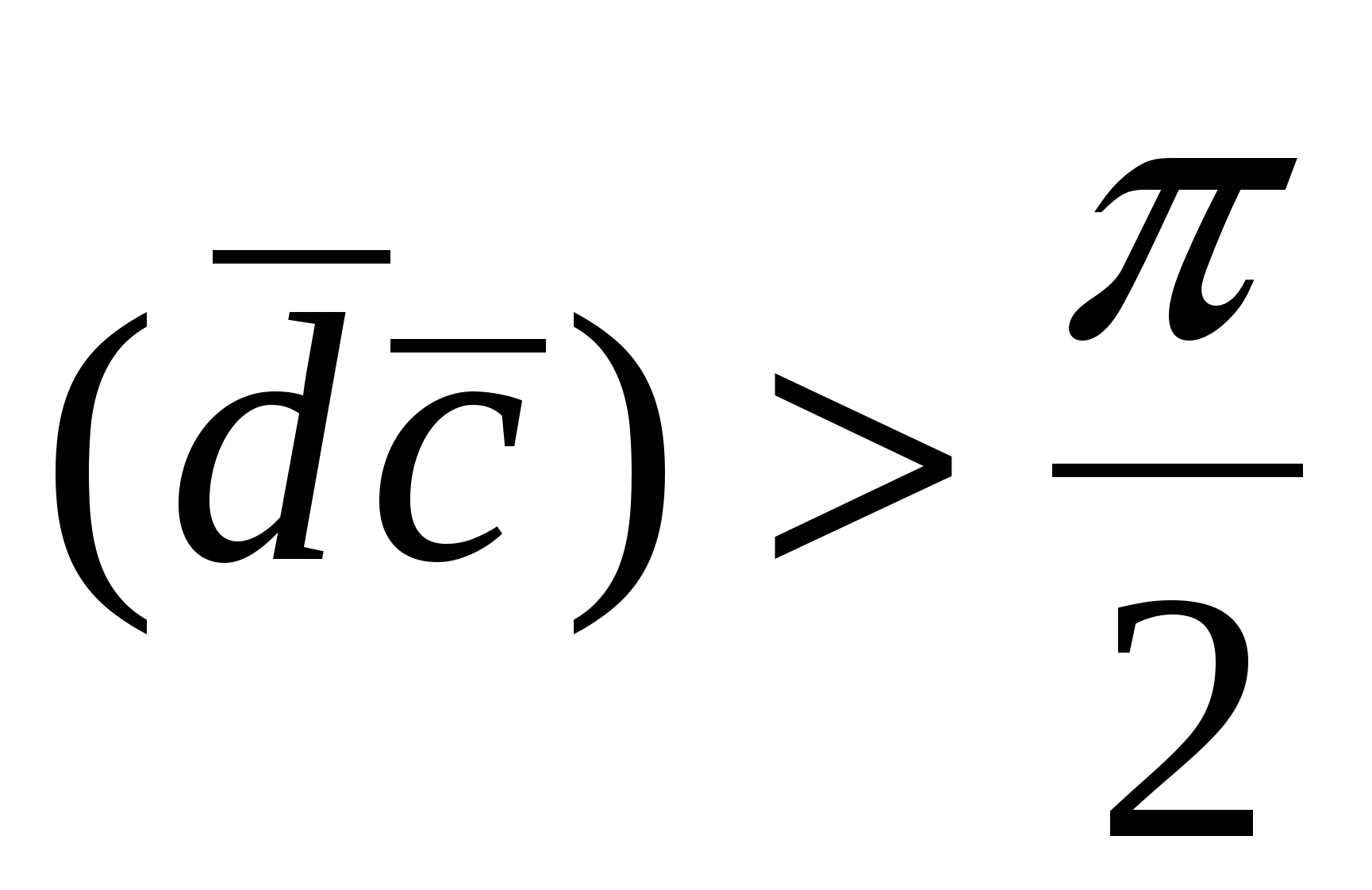 ), следовательно, произведение ), следовательно, произведение 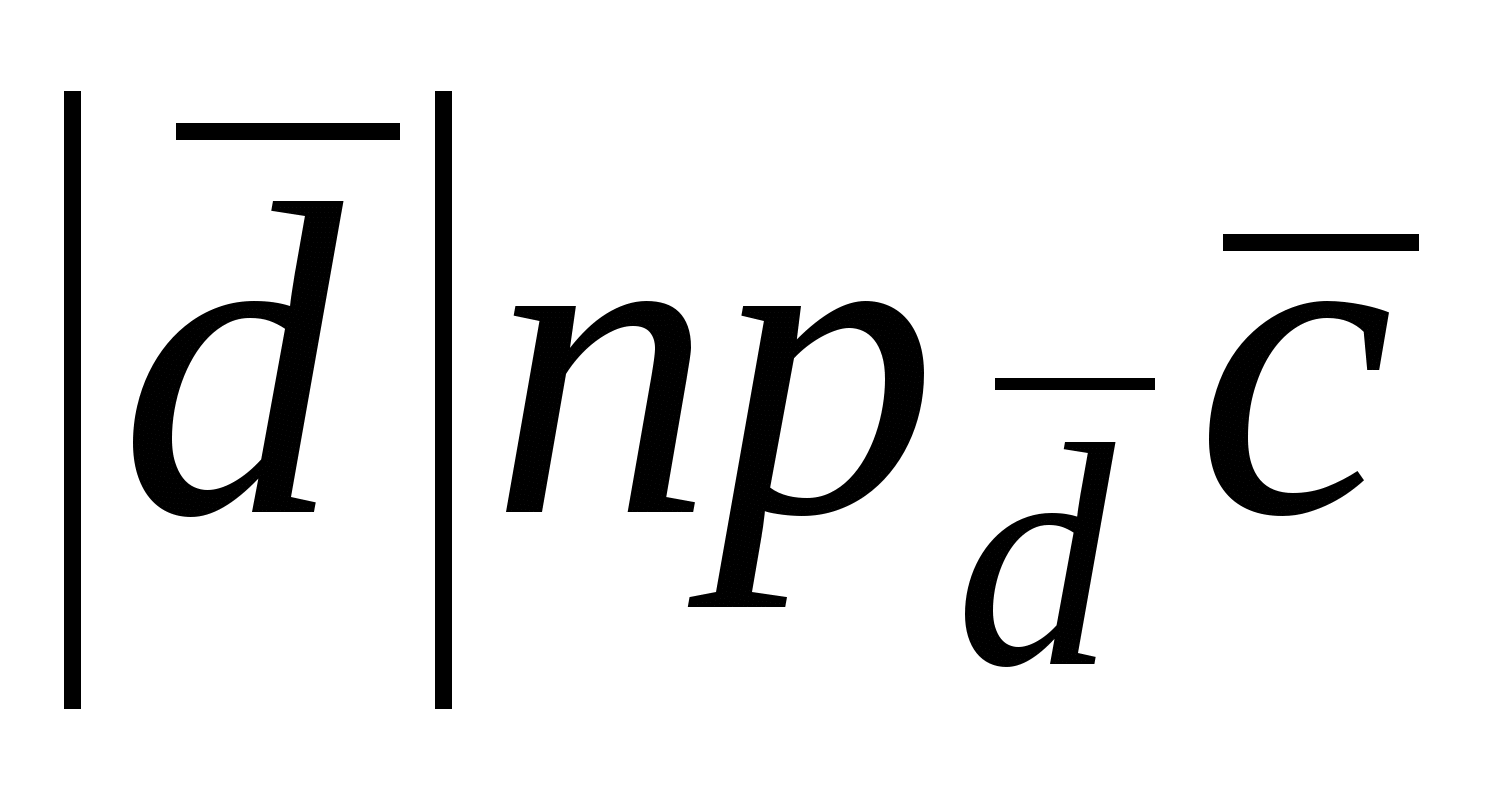 равно объему параллелепипеда со знаком «+» или «–». Из рис.18 видно, что равно объему параллелепипеда со знаком «+» или «–». Из рис.18 видно, что 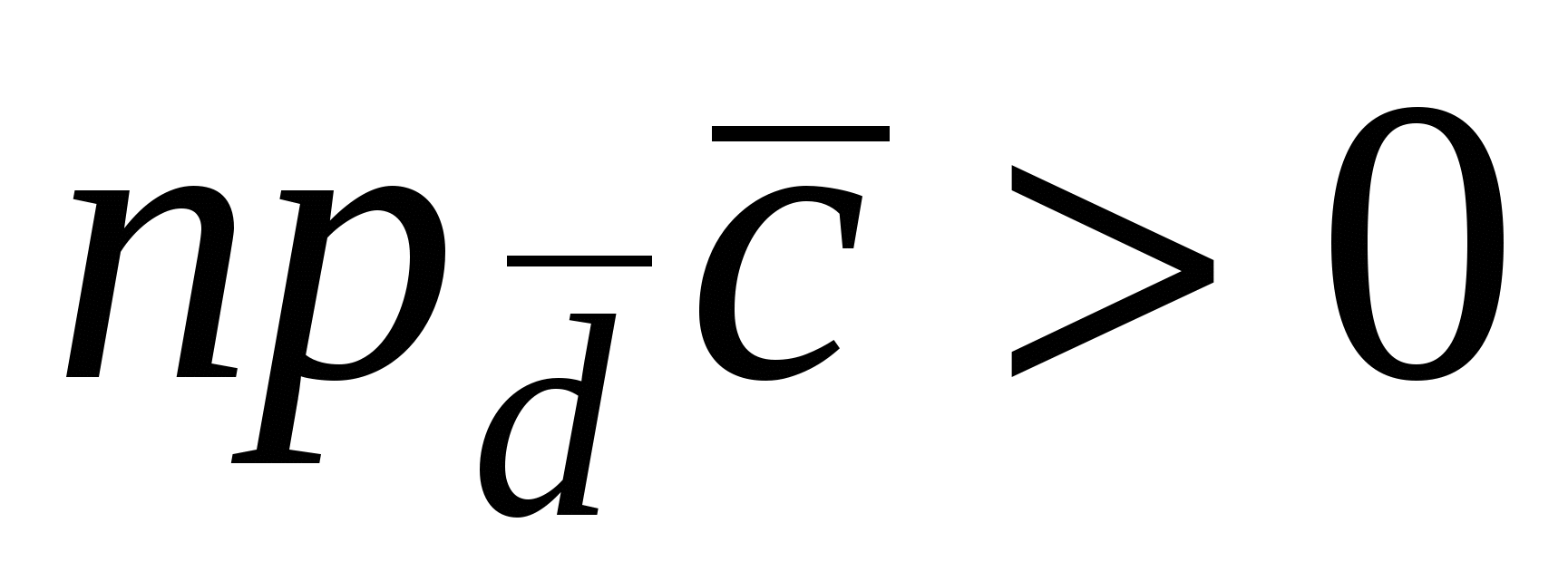 , если упорядоченная тройка векторов , если упорядоченная тройка векторов 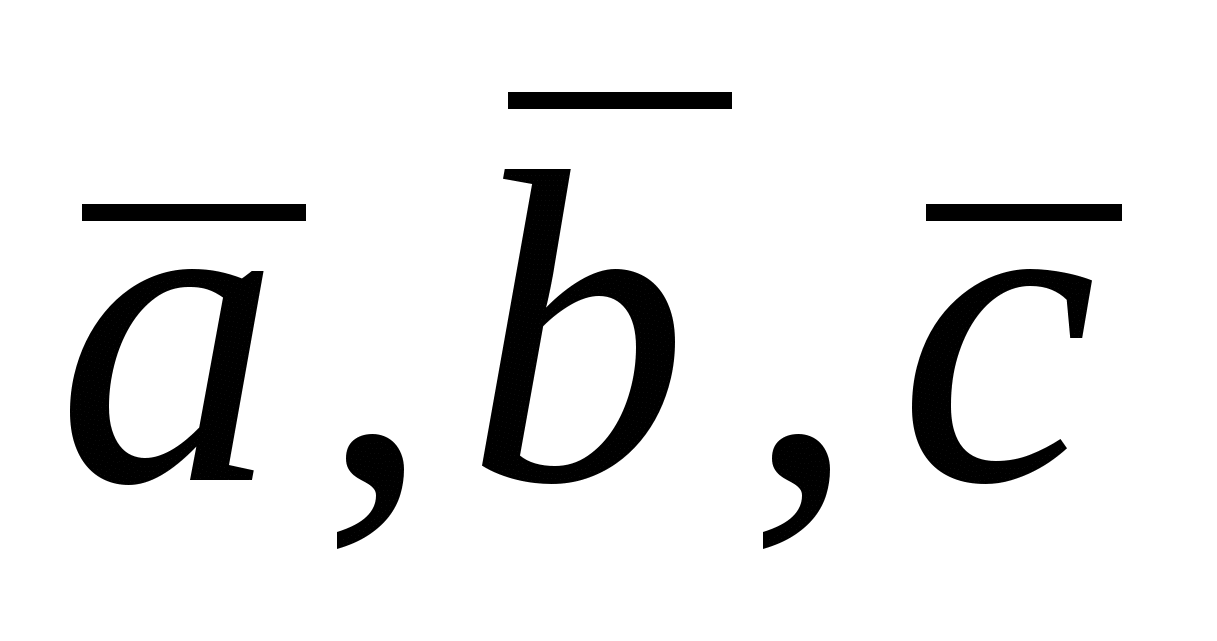 – правая, если векторы – правая, если векторы 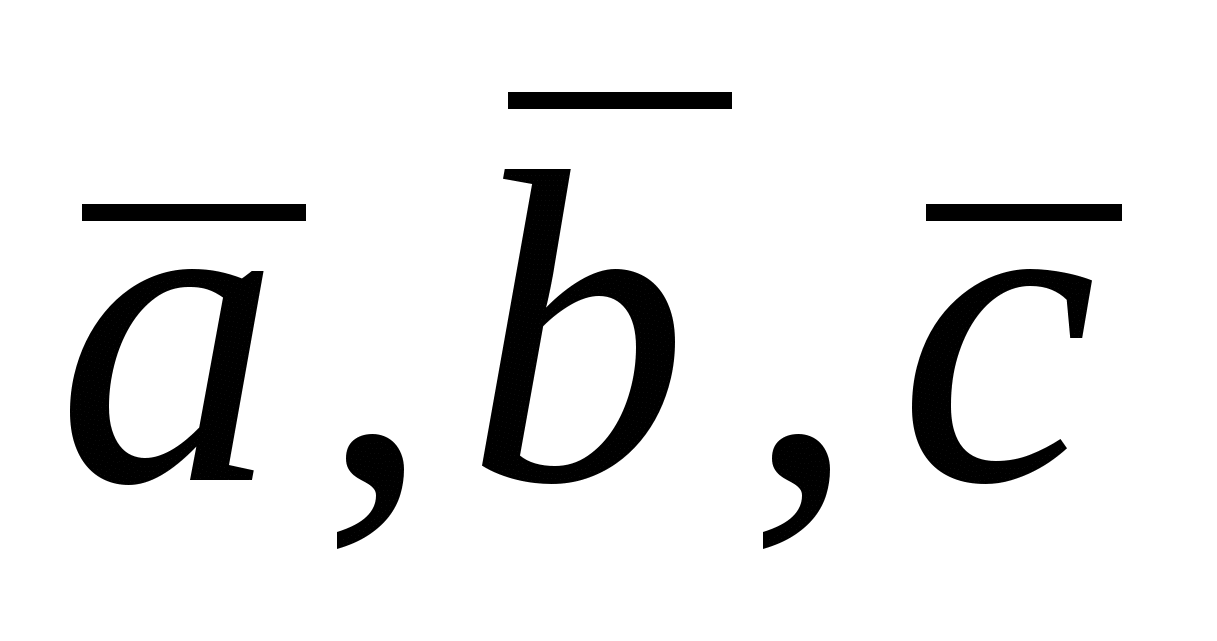 образуют левую тройку, то образуют левую тройку, то 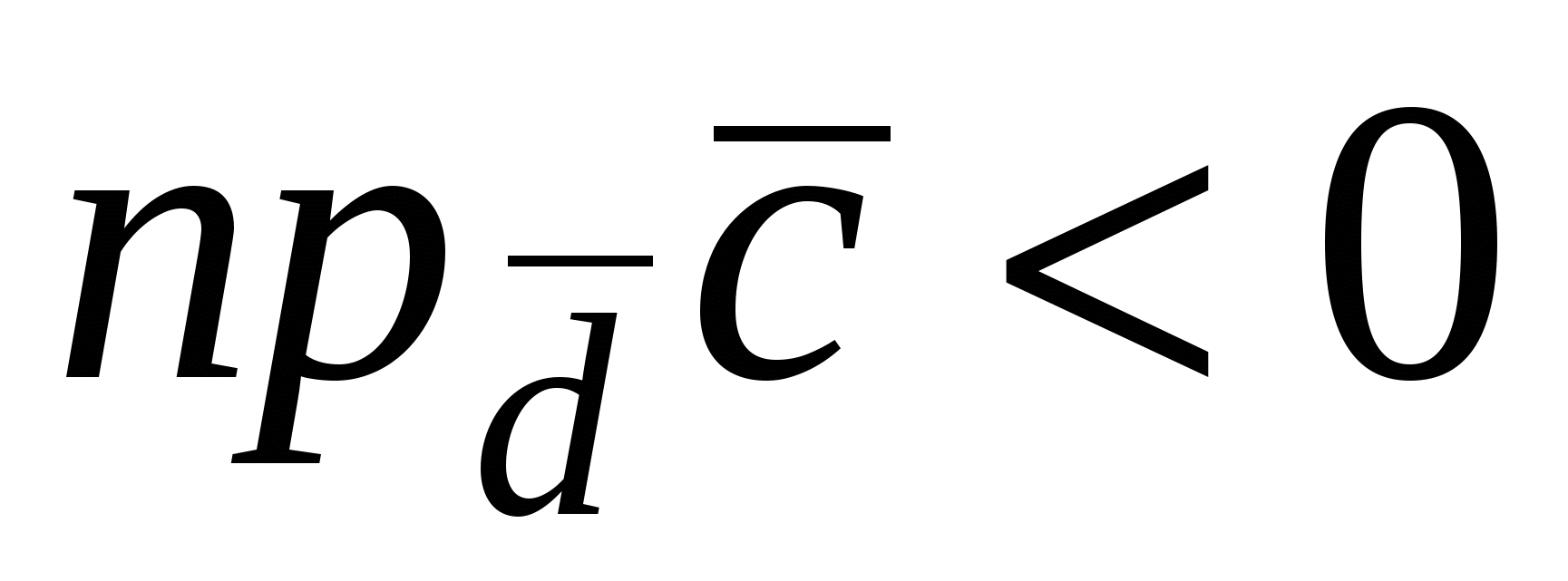 . Таким образом, смешанное произведение векторов . Таким образом, смешанное произведение векторов 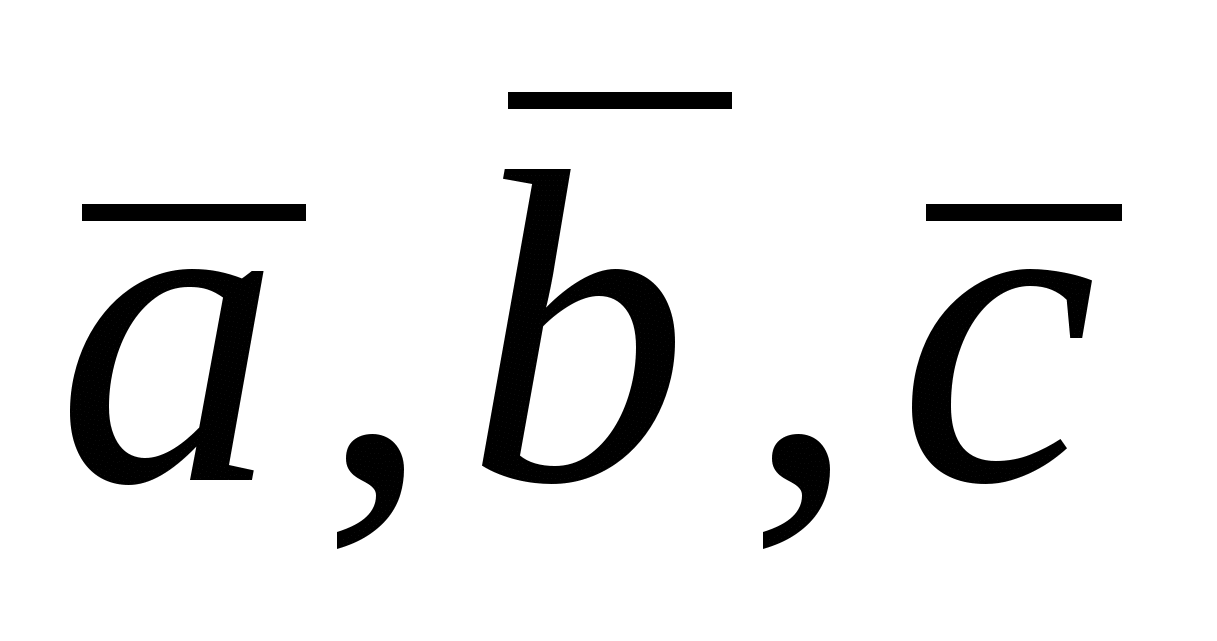 равно объему параллелепипеда, построенному на этих векторах, со знаком плюс, если тройка векторов равно объему параллелепипеда, построенному на этих векторах, со знаком плюс, если тройка векторов 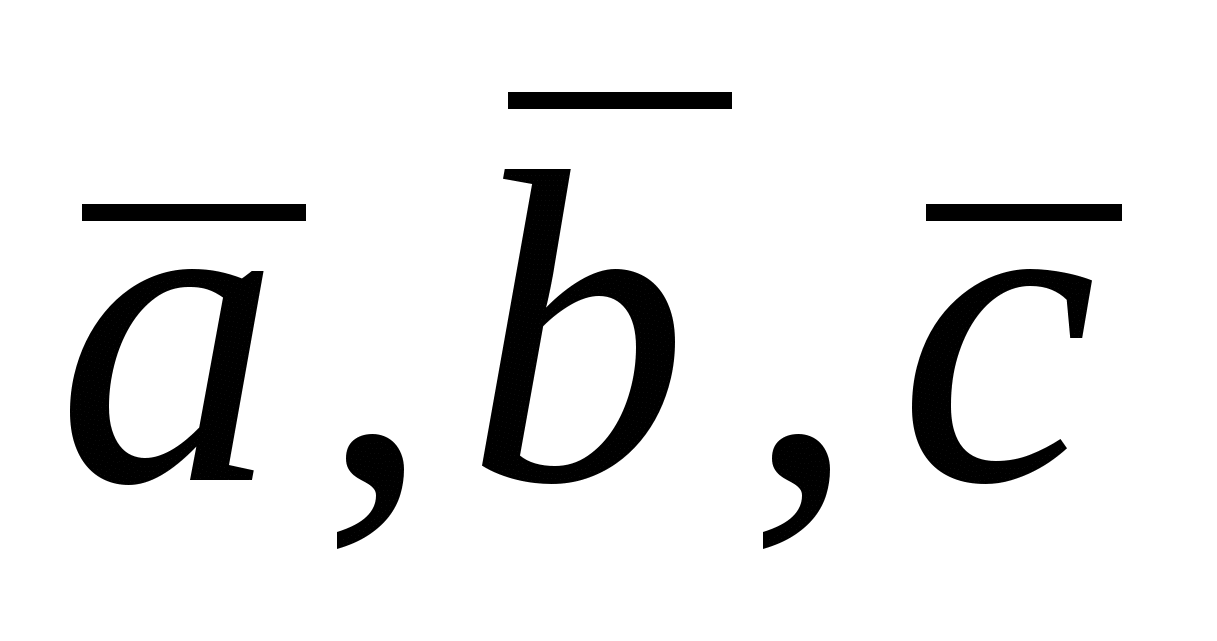 правая, и со знаком минус, если эта тройка – левая. правая, и со знаком минус, если эта тройка – левая.
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ В
ОРТОНОРМИРОВАННОМ БАЗИСЕ
Пусть 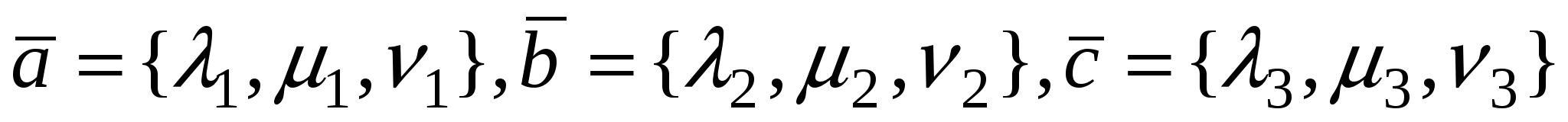 , тогда вектор , тогда вектор 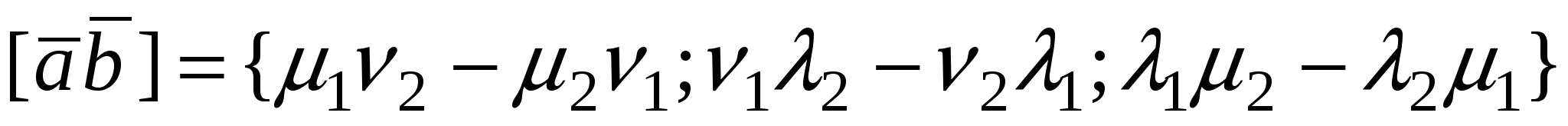 .Смешанное произведение .Смешанное произведение 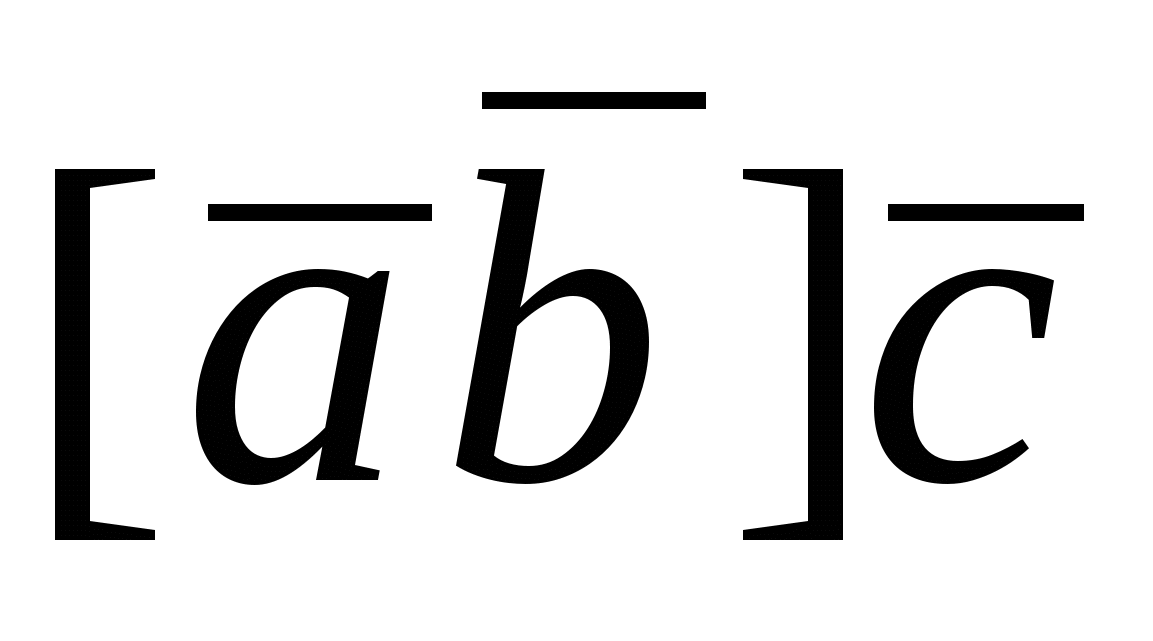 есть скалярное произведение векторов есть скалярное произведение векторов 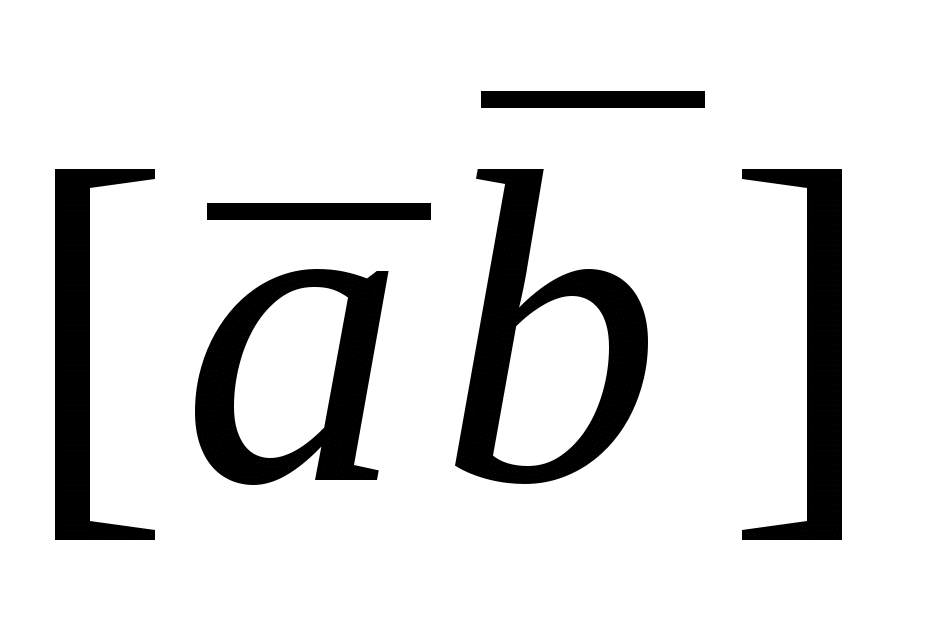 и и 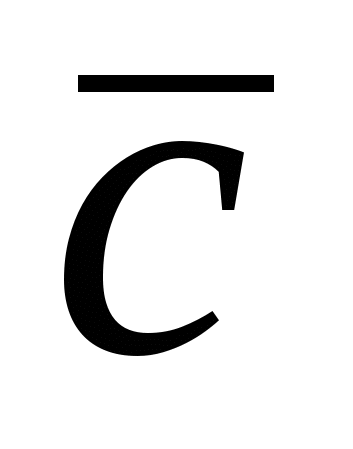 , поэтому , поэтому 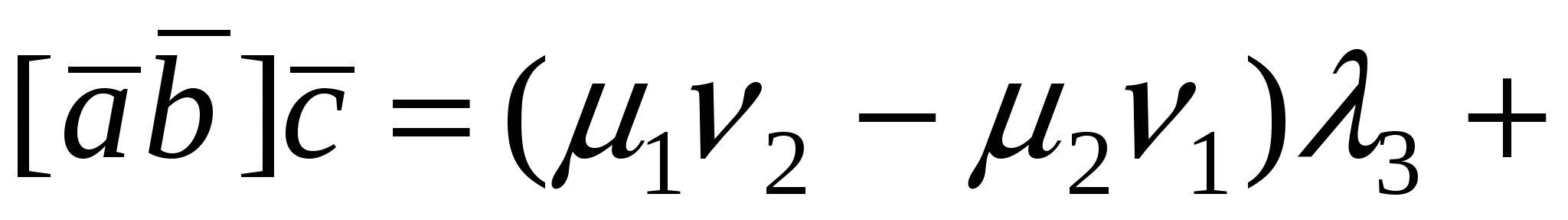 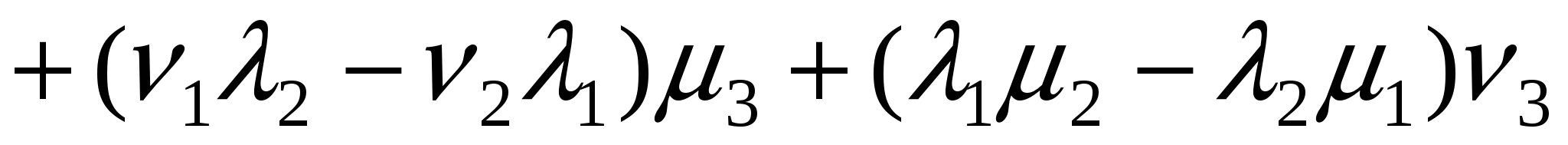 . .
Если использовать символы определителей второго и третьего порядков, то последнее выражение можно представить в виде:
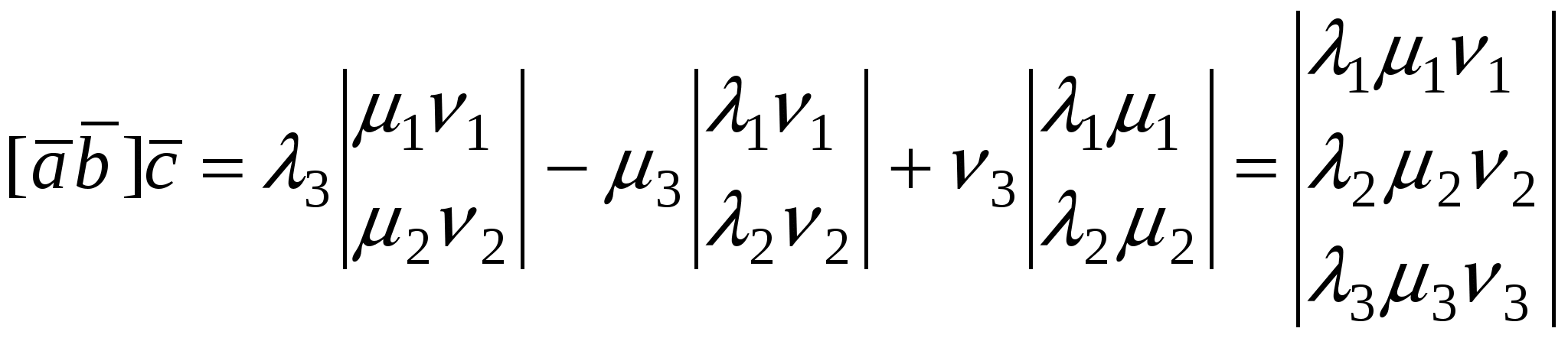 . .
Следовательно, смешанное произведение 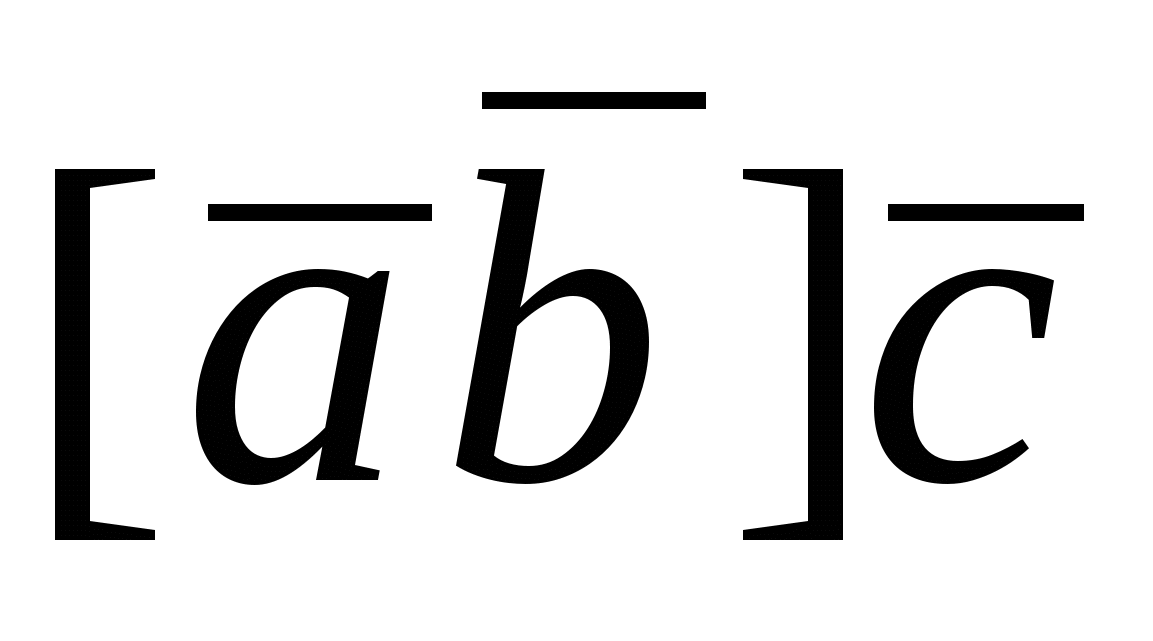 в ортонормированном базисе равно определителю третьего порядка, где первые две строки состоят из координат сомножителей вектора в ортонормированном базисе равно определителю третьего порядка, где первые две строки состоят из координат сомножителей вектора 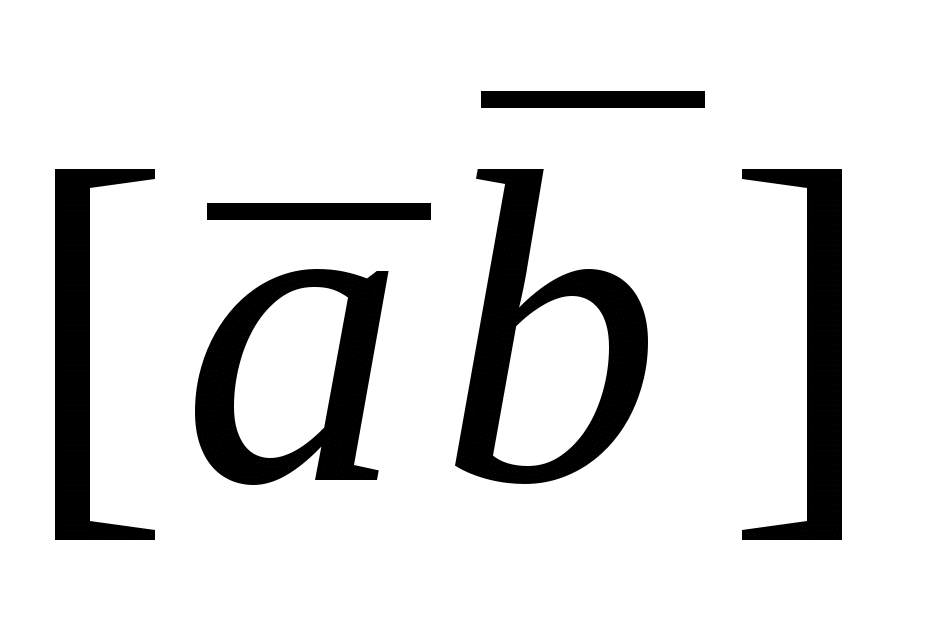 , а третья - из координат вектора , а третья - из координат вектора 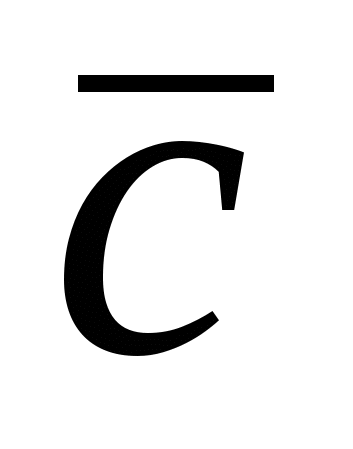 . .
СВОЙСТВА СМЕШАННОГО ПРОИЗВЕДЕНИЯ
1. 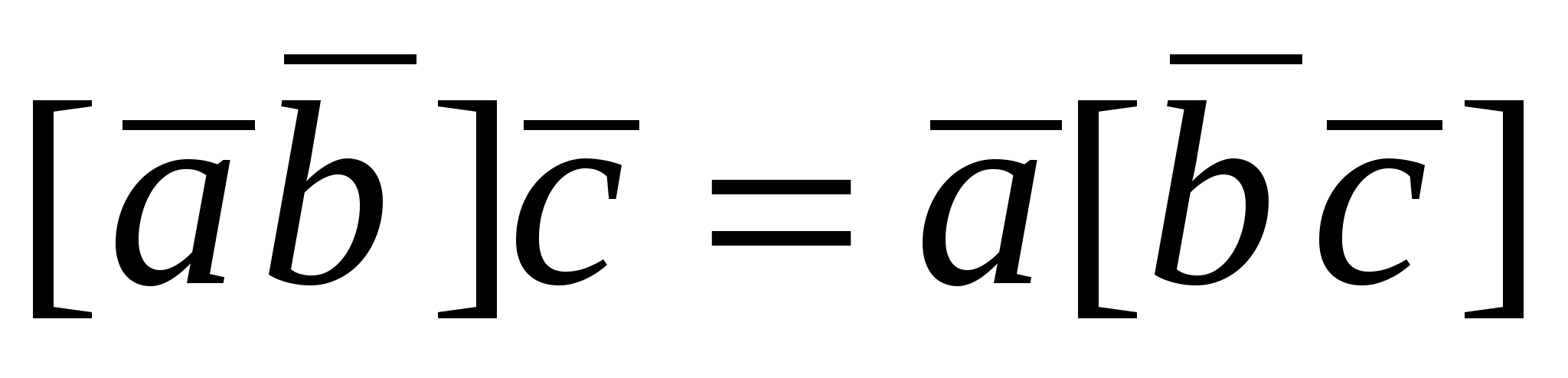 . Это свойство позволяет записывать смешанное произведение векторов . Это свойство позволяет записывать смешанное произведение векторов 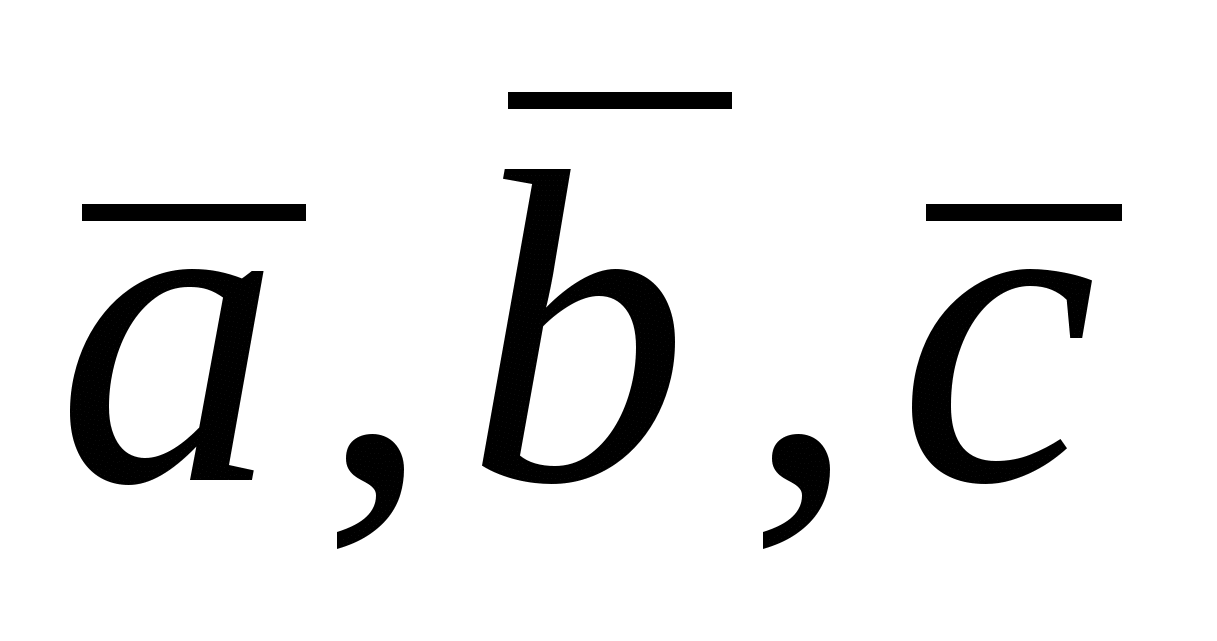 в виде в виде 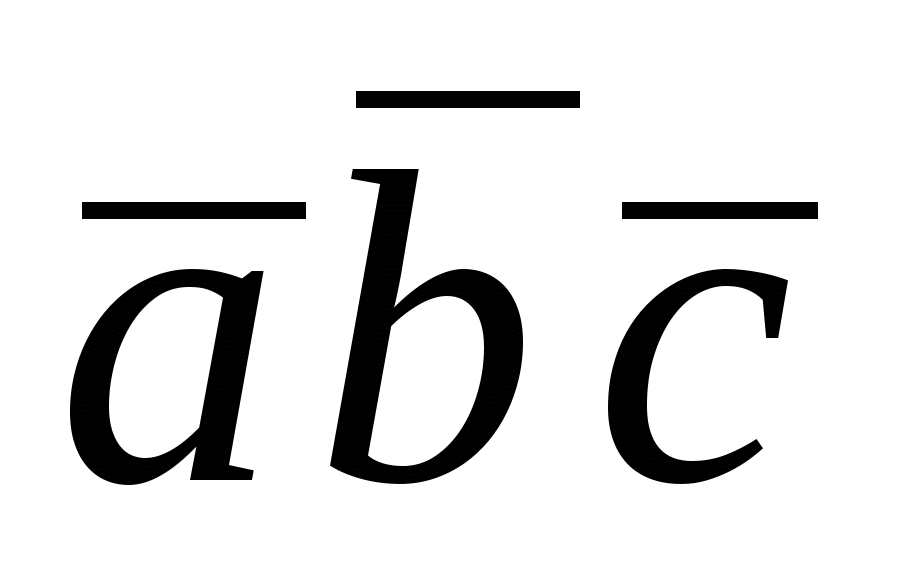 , не указывая, какие два вектора (первые или последние) перемножаются векторно. , не указывая, какие два вектора (первые или последние) перемножаются векторно.
2. 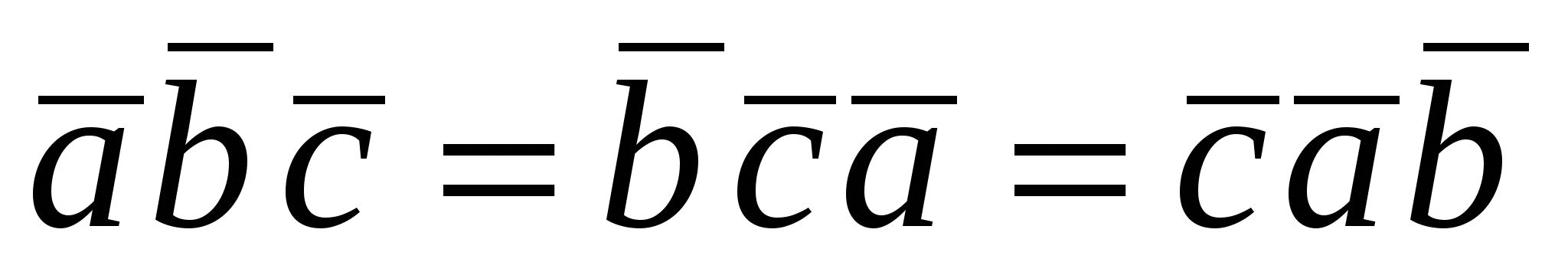 . Значение смешанного произведения не меняется при циклической (круговой) перестановке множителей. . Значение смешанного произведения не меняется при циклической (круговой) перестановке множителей.
3. 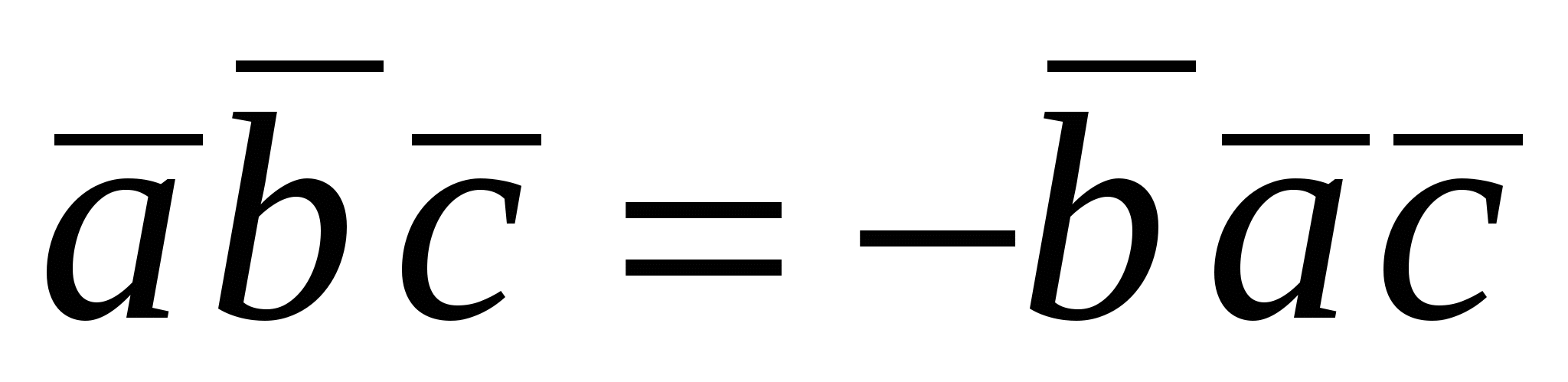 . Значение смешанного произведения меняет знак, если поменять местами два сомножителя. . Значение смешанного произведения меняет знак, если поменять местами два сомножителя.
ДОКАЗАТЕЛЬСТВО СВОЙСТВ СМЕШАННОГО ПРОИЗВЕДЕНИЯ
1. Пусть 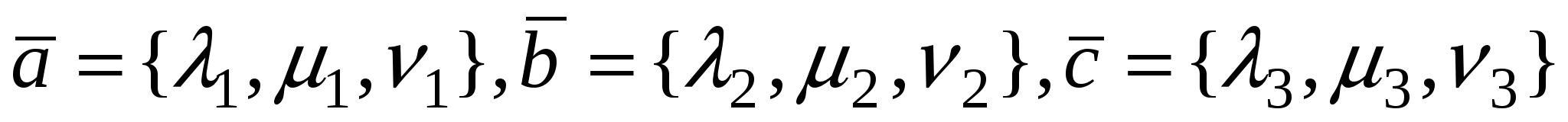 ; из переместительного свойства скалярного произведения следует, что ; из переместительного свойства скалярного произведения следует, что
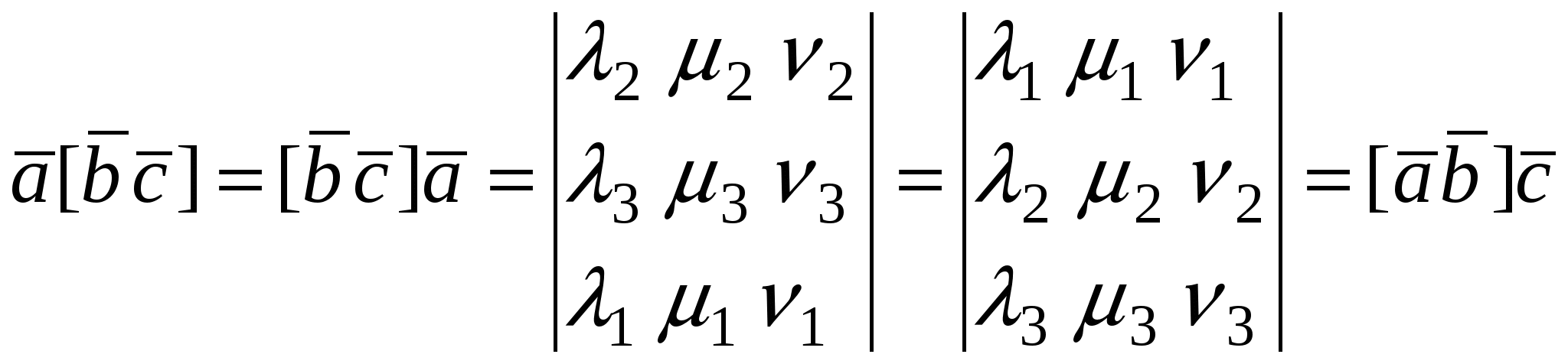
(следует дважды поменять местами строки, чтобы из первого определителя получить второй).
2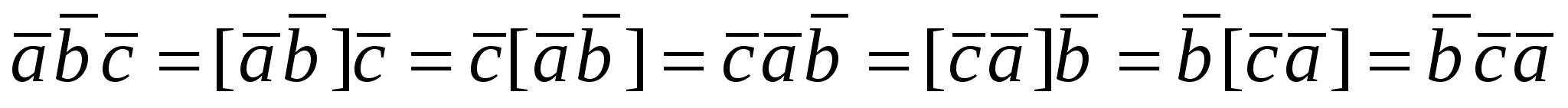 . .
3. 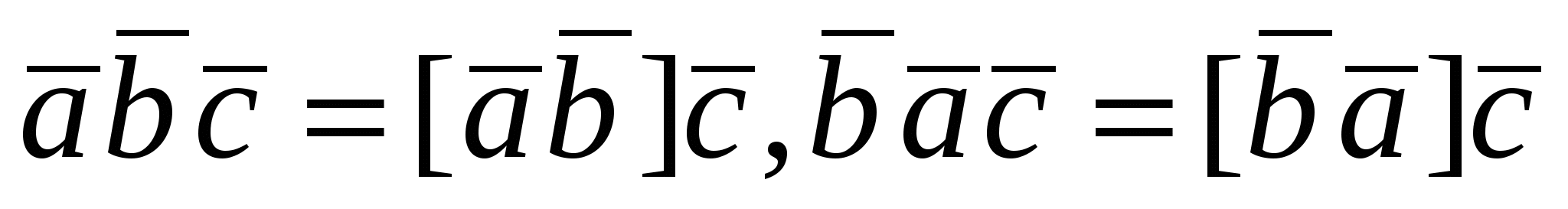 , но , но 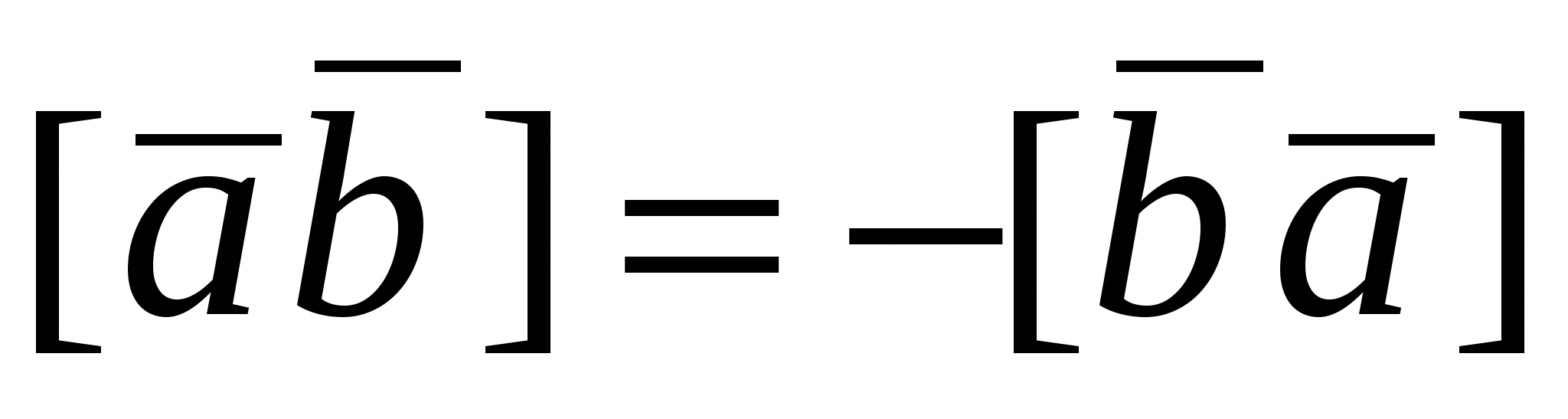 , следовательно, , следовательно, 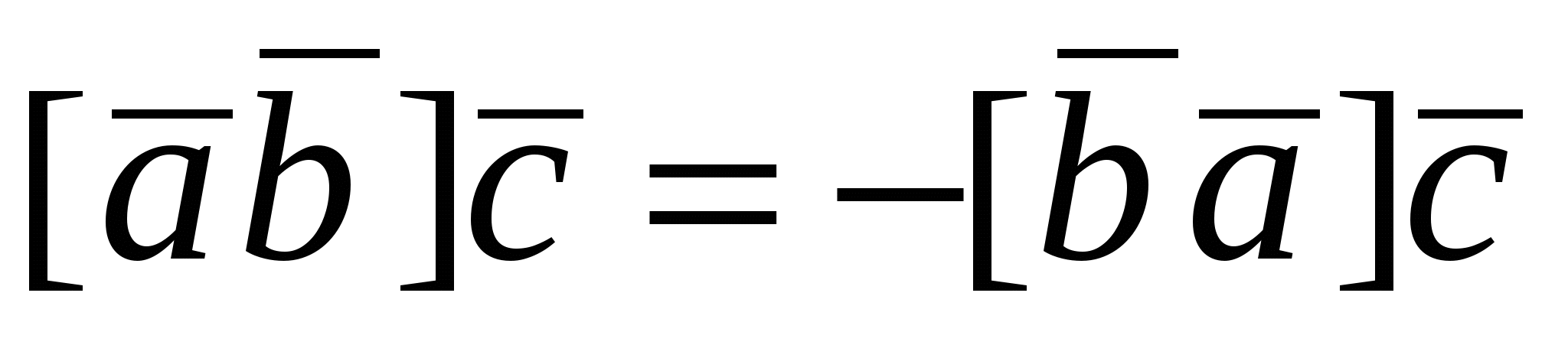 или или 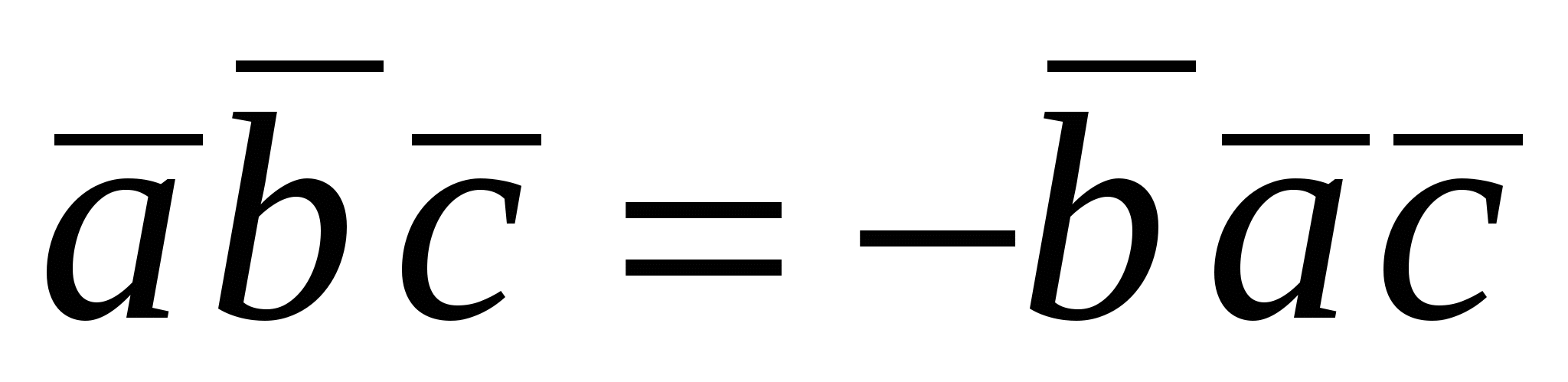 . .
УСЛОВИЕ КОМПЛАНАРНОСТИ ТРЕХ ВЕКТОРОВ
Теорема. Векторы 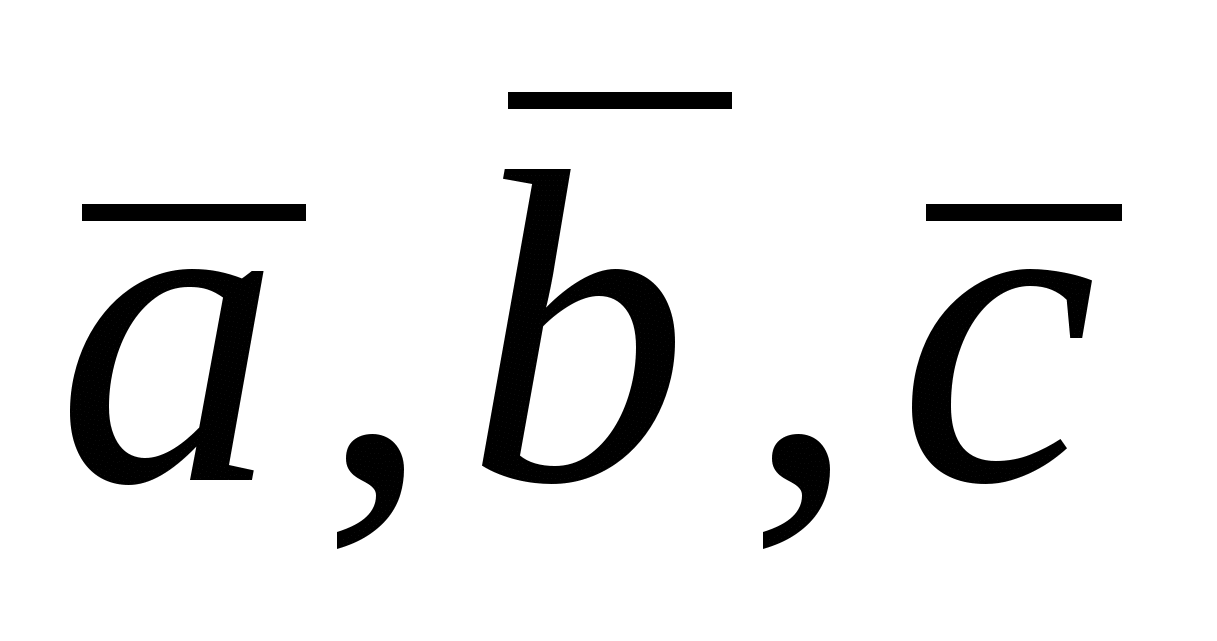 компланарны тогда и только тогда, когда компланарны тогда и только тогда, когда 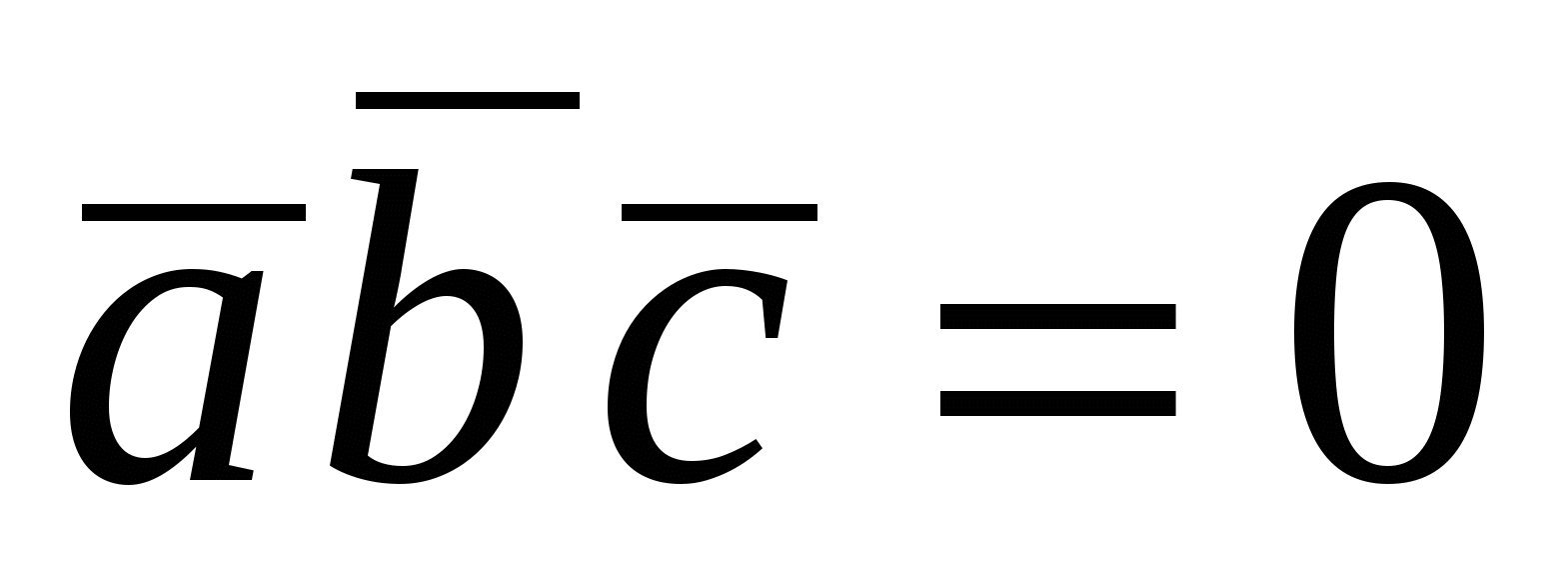 . .
Доказательство необходимости условия.
|
 Скачать 0.68 Mb.
Скачать 0.68 Mb. .
.

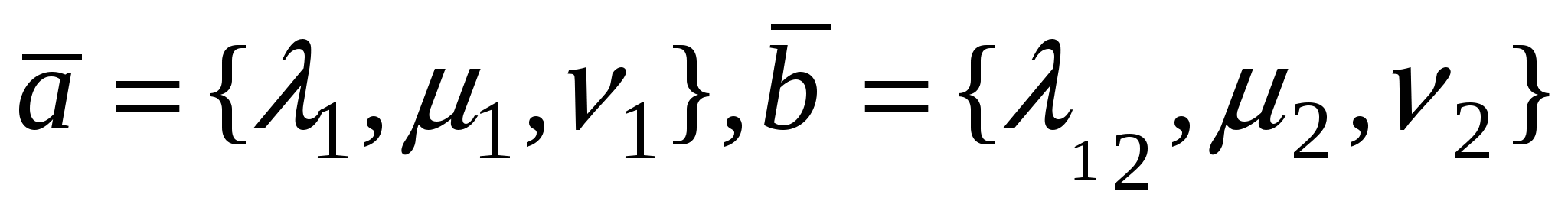 . Рассмотрим вектор
. Рассмотрим вектор 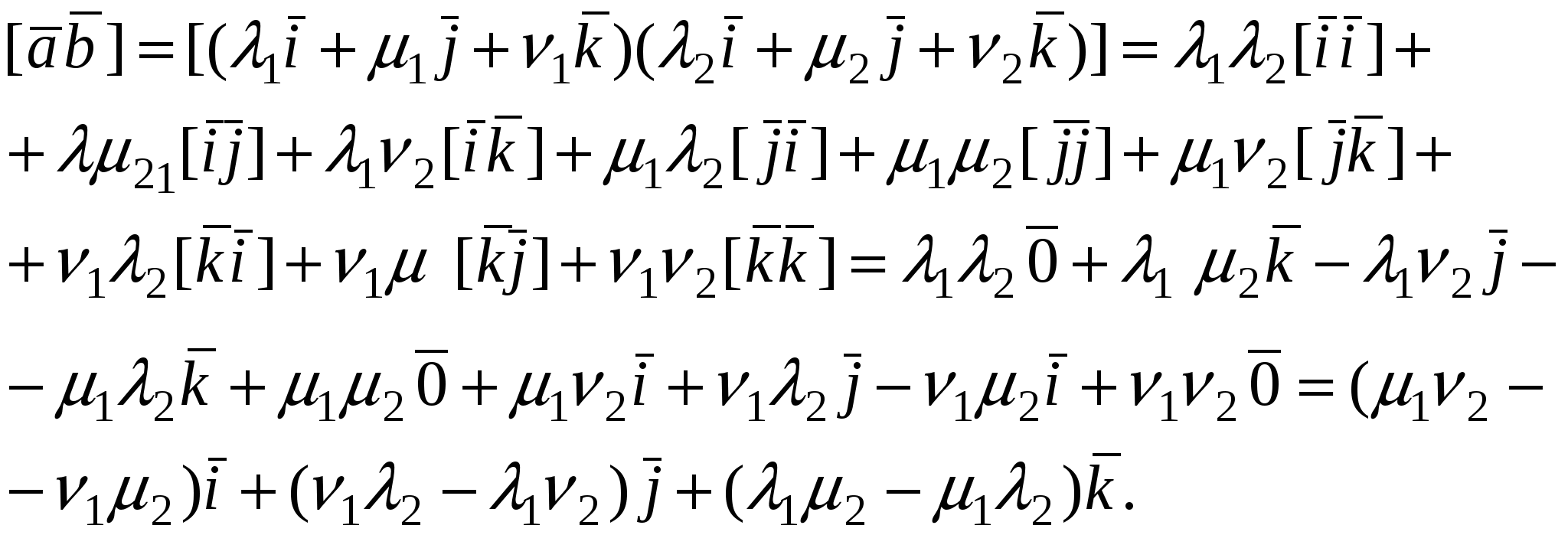
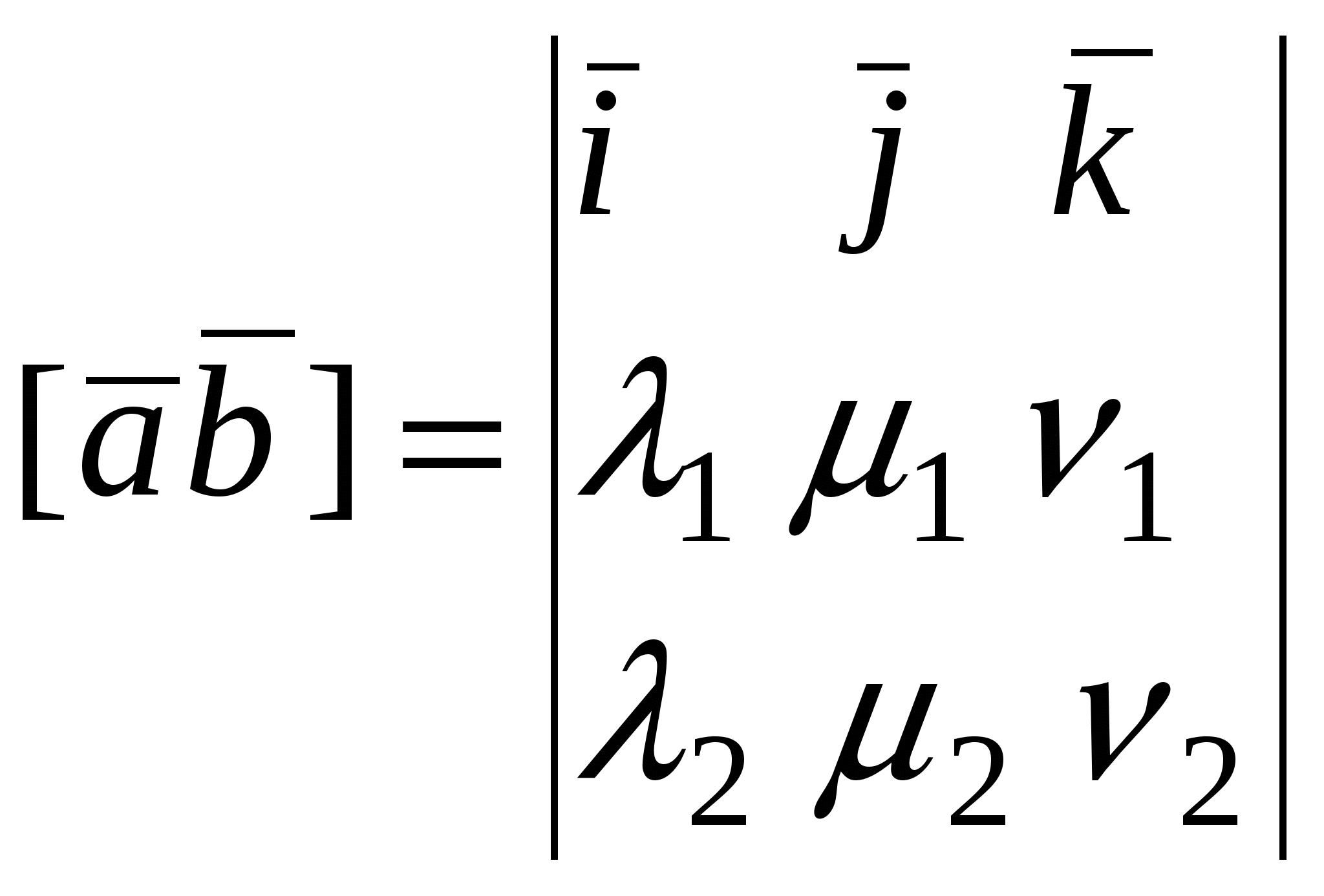 .
.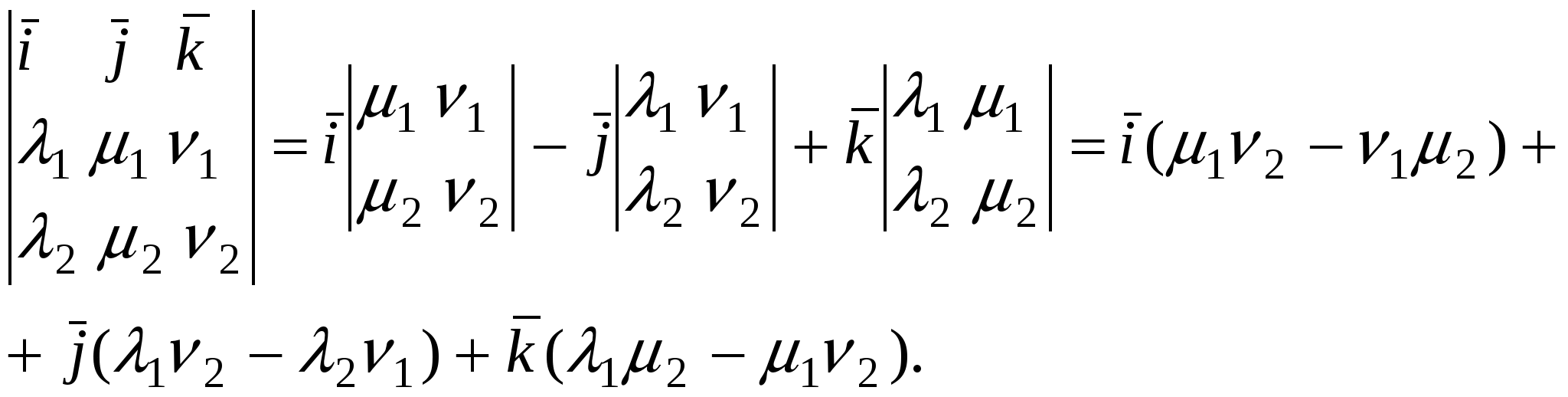
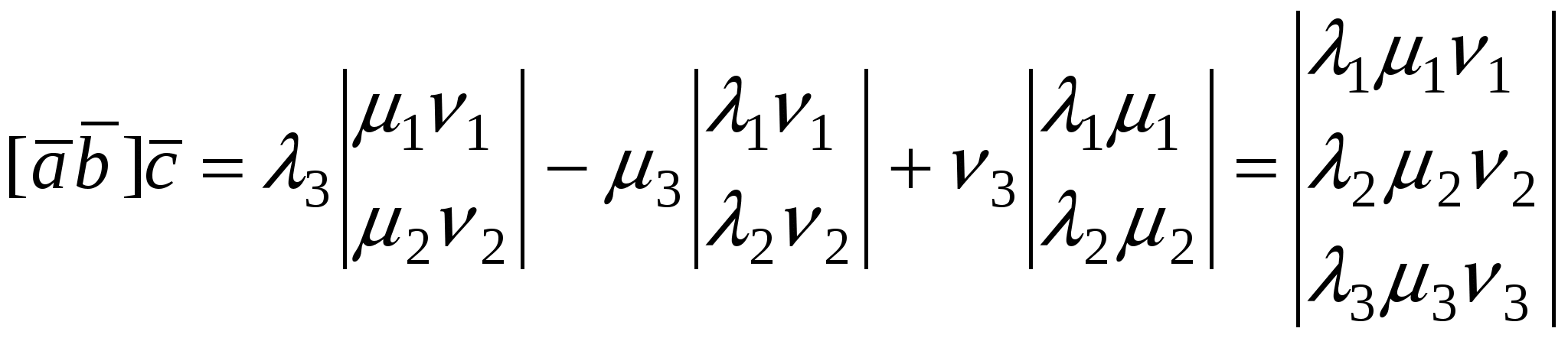 .
.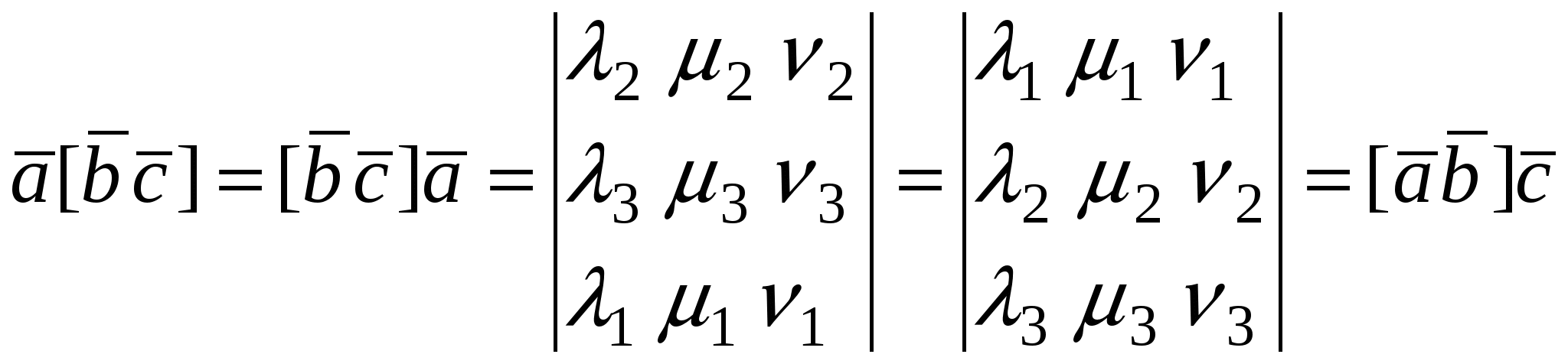

 D C
D C
 Рис. 14.
Рис. 14. 