Межпредметные связи. Доклад Межпредметные связи. Слайд 2 вступление
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
|
СЛАЙД 2 ВСТУПЛЕНИЕ По результатам Международных исследований среди выпускников 9-11 классов, проведенных в 65 странах мира, Россия заняла 37 место по оценке качества математического образования. Каковы причины таких низких результатов? У 70-80% обучающихся отсутствовали умения самостоятельной работы; 60% - не умели выделять существенные признаки, понятия, приводить примеры; 70% - заучивали материал в полном объеме на репродуктивном уровне усвоения знаний, вследствие чего выпускники проявили низкий уровень учебной мотивации. Основной проблемой образовательных достижений по математике российских школьников явилось противоречие между высокими предметными знаниями и умениями, с одной стороны, и затруднениями в применении этих знаний в ситуациях, близких к повседневной жизни, а также в работе с информацией, представленной в различной форме.  СЛАЙД 3 Стандарты второго поколения предъявляют новые, современные требования к учебному процессу. Учитель математики, начинающий реализовывать Стандарт на ступени основного образования, должен внести изменения в свою деятельность, в построение урока и его проведение. При проектировании эффективного урока необходимо учитывать особенности реализации межпредметных связей в соответствии с требованиями ФГОС. Все указанное выше и определяет актуальность выбранной темы работы. Объект: межпредметные связи в обучении. Предмет исследования: анализ и решение проблем, связанных с реализацией межпредметных связей в обучении математике Цель работы: разработать формы реализации межпредметных связей математики, физики и информатики, направленных на повышение уровня и качества образования обучающихся.  СДАЙД 4 В педагогической литературе имеется более 30 определений категории «межпредметные связи», существуют самые различные подходы к их педагогической оценке и различные классификации. Одним из более полных определений является следующее: межпредметные связи есть педагогическая категория для обозначения синтезирующих, интегративных отношений между объектами, явлениями и процессами реальной действительности, нашедших свое отражение в содержании, формах и методах учебно-воспитательного процесса и выполняющих образовательную, развивающую и воспитывающую функции в их ограниченном единстве.  СЛАЙД 5 Методологическая функция выражена в том, что только на их основе возможно формирование у учащихся диалектико-материалистических взглядов на природу, современных представлений о ее целостности и развитии, поскольку межпредметные связи способствуют отражению в обучении методологии современного естествознания, которое развивается по линии интеграции идей и методов с позиций системного подхода к познанию природы. Образовательная функция межпредметных связей состоит в том, что с их помощью учитель формирует такие качества знаний учащихся, как системность, глубина, осознанность, гибкость. Межпредметные связи выступают как средство развития математических понятий, способствуют усвоению связей между ними и общими понятиями. Развивающая функция межпредметных связей определяется их ролью в развитии системного и творческого мышления учащихся, в формировании их познавательной активности, самостоятельности и интереса к познанию математики. Межпредметные связи помогают преодолеть предметную инертность мышления и расширяют кругозор учащихся. Воспитывающая функция межпредметных связей выражена в их содействии всем направлениям воспитания школьников в обучении математики Учитель математики, опираясь на связи с другими предметами, реализует комплексный подход к воспитанию. Конструктивная функция межпредметных связей состоит в том, что с их помощью учитель совершенствует содержание учебного материала, методы и формы организации обучения. Реализация межпредметных связей требует совместного планирования учителями предметов естественнонаучного цикла комплексных форм учебной и внеклассной работы, которые предполагают знания ими учебников и программ смежных предметов. 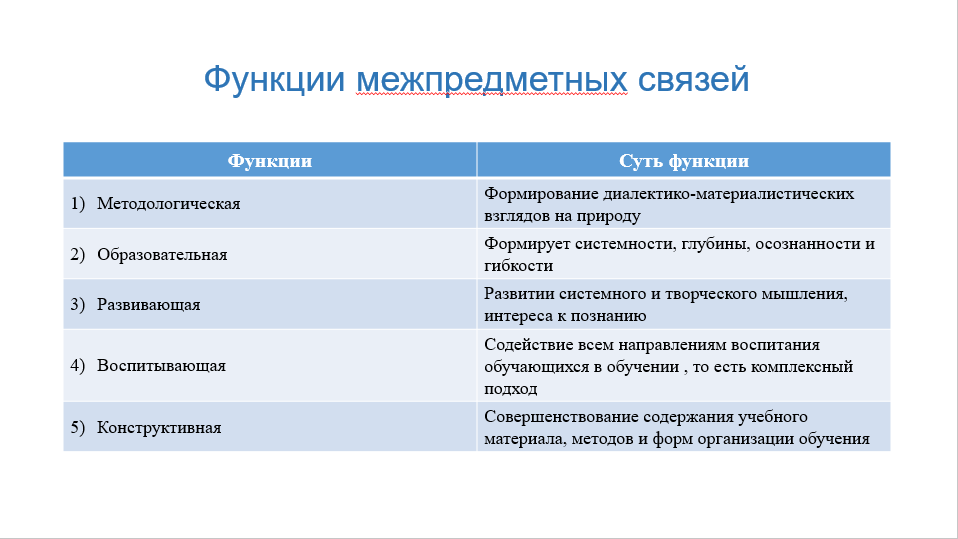 СЛАЙДЫ 6,7 Рассмотрим теперь классификацию межпредметных связей, так как правильная классификация, отображая закономерности развития классифицируемых понятий, глубоко вскрывает связи между ними, способствует созданию научно-практических предпосылок для реализации этих связей в учебном процессе. Межпредметные связи характеризуются, прежде всего, своей структурой, а поскольку внутренняя структура предмета является формой, то мы можем выделить следующие формы связей: Межпредметные связи по составу показывают — что используется, трансформируется из других учебных дисциплин при изучении конкретной темы. Межпредметные связи по направлению показывают: 1) является ли источником межпредметной информации для конкретно рассматриваемой учебной темы, изучаемой на широкой межпредметной основе, один, два или несколько учебных предметов. 2) Используется межпредметная информация только при изучении учебной темы базового учебного предмета (прямые связи), или же данная тема является также «поставщиком» информации для других тем, других дисциплин учебного плана (обратные или восстановительные связи). Временной фактор показывает: какие знания, привлекаемые из других дисциплин, уже получены учащимися, а какой материал еще только предстоит изучать в будущем (хронологические связи); какая тема в процессе осуществления межпредметных связей является ведущей по срокам изучения, а какая ведомой (хронологические синхронные связи). как долго происходит взаимодействие тем в процессе осуществления межпредметных связей. Вышеприведенная классификация межпредметных связей позволяет аналогичным образом классифицировать внутрикурсовые связи (связи, например, между физикой, математикой, информатикой — курса физики; связи между неорганической и органической химией — курса химии...), а также внутрипредметные связи между темами определенного учебного предмета, например физики, органической химии, новейшей истории. Во внутрикурсовых и внутри-предметных связях из хронологических видов преобладают преемственные и перспективные виды связей, тогда как синхронные резко ограничены, а во внутрипредметных связях синхронный вид вообще отсутствует СЛАЙД 8 На основе знаний по математике в первую очередь формируются общепредметные расчётно-измерительные умения. Преемственные связи с курсами естественного цикла раскрывают практическое применение математических умений и навыков. Это способствует формированию у учащихся целостного, научного мировоззрения. В свою очередь, математические задачи можно рассматривать как средство познания мира, так как, решая непосредственно задачи по математике, учащиеся через условия задачи знакомятся с природными явлениями, веществами, телами. 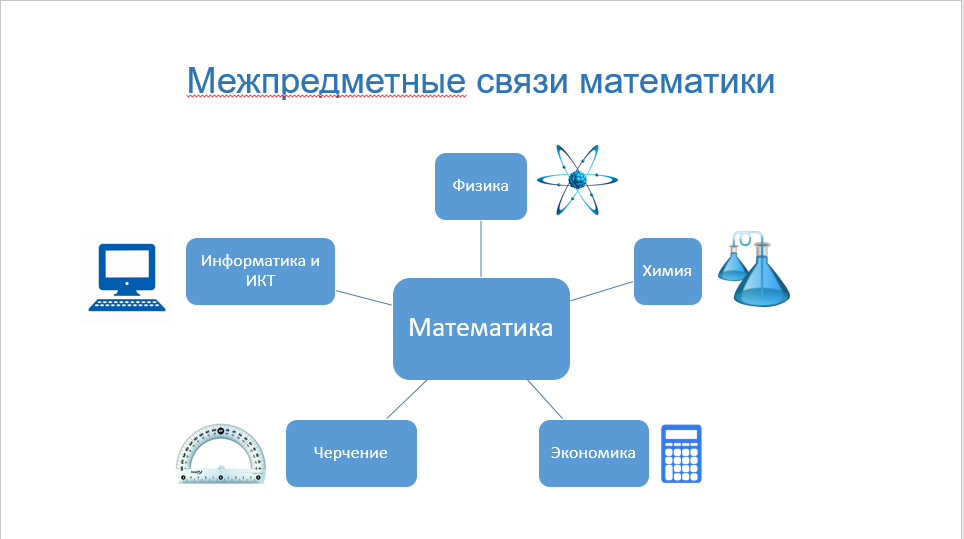 СЛАЙД 9, 10   СЛАЙД 11  СЛАЙД 12  СЛАЙД 13  СЛАЙД 14 Временное несоответствие школьных программ. Практика показывает, что на сегодняшний день явно выражена временная несогласованность прохождения учебного материала по физике и математике. Например, возьмём тему «Векторы» в гео- метрии и тему «Кинематика», изучаемую в физике девятого класса, а также тему «Скорость» и тему «Сила» в курсе физики седьмого класса. Сразу отметим, что при изучении понятий силы и скорости учащиеся седьмого класса получают информацию о векторных ве- личинах. Только практически более чем через год учёбы в начале девятого класса в теме «Кинематика» учащийся знакомится с осно- вами векторной алгебры, учится складывать и вычитать векторы значительно раньше, чем на уроках геометрии. Это временное не- соответствие узаконено поурочным тематическим планированием для базового уровня образования. Понятийное несоответствие школьных программ. Кроме рассмотренного выше временного несоответствия при- сутствует и понятийная несогласованность школьных программ по физике и математике, в этих дисциплинах различается понятийна трактовка в учебниках, а также по-разному трактуются и обозначаются отдельные термины. Опять сравним тему «Векторы» в геометрии, темы «Скорость», «Сила» в курсе физики седьмого класса и тему «Кинематика» в курсе физики девятого класса. В курсе физики седьмого класса векторные величины определялись как физические величины, имеющие направление, а не только величину. Доучившись до девятого класса, ученики в курсе геометрии получали информацию о перемещении, которое определялось как отображение плоскости на себя, сохраняющее расстояние. Там же рассматривается операция параллельного переноса как частный случай перемещения. Однако ни само перемещение, ни операция параллельного переноса совершенно не ассоциируются в сознании учащихся с понятием вектора, которое вводится в курсе физики. Это противоречие снимается только при интенсивной дополнительной работе учителя высшей категории.  Слайд 15  Слайд 16  Слайд 17 Таким образом, учебный процесс преподавания требует использования межпредметных связей физики и математики, а именно: сочетания теоретических методов изучения физики с экспериментальными методами на основе доступных понятий элементарной математики. Этот подход обеспечивает одновременно достижение высокого уровня усвоения математики, формирует критическое и логическое мышление учеников, а также способствует пониманию единства материального мира. У учащихся появляется понимание того, что математические формулы и уравнения реально воплощаются в жизнь в физических процессах. Реализация межпредметных связей математики с другими предметами способствует систематизации, а, следовательно, глубине и прочности знаний, помогает дать ученикам целостную картину мира, сокращает общее время на изучение темы, что позволяет более глубокое и детальное изучение. Однако эти связи между отдельными предметами имеют свою специфику, которая накладывает отпечаток на преподавание, в связи с чем остается множество еще нерешенных вопросов и задач по этой тем |
