Урок алгебры по теме Преобразования выражений, содержащих арифметические квадратные корни. для буклета. Смысловое чтение на уроках математики
 Скачать 52.81 Kb. Скачать 52.81 Kb.
|
|
Смысловое чтение на уроках математики Читать – это ещё ничего не значит; что читать и как понимать читаемое – вот в чём главное дело. К.Д. Ушинский Человек живет в информационном обществе, где очень важно уметь самостоятельно действовать в тех или иных ситуациях, принимать решения, адаптироваться к стремительно меняющимся условиям жизни. Поэтому перед школой ставится задача, воспитывать личность, способную: ориентироваться в меняющихся жизненных ситуациях, уметь самому приобретать необходимые знания и применять их на практике для решения возникших вопросов; уметь, применяя современные технологии, видеть возникающие проблемы и искать пути их решения; уметь критически мыслить, иметь четкое представление о том, где и как будут применяться полученные знания, творчески мыслить, воспроизводить новые идеи; осуществлять грамотную работу с информацией (собирать факты, проводить их рефлексию, делать важные обобщения, приводить аргументированные выводы); быть общительным, уметь общаться сообща в различных областях и ситуациях, находить выход из конфликтных ситуаций; самостоятельно работать над развитием собственного интеллекта, культурного уровня, грамотности. Какой же должна быть математика, чтобы все учащиеся полюбили этот предмет? На уроке желательно создать ситуацию, в которой дети приобретают знания в процессе активной познавательной деятельности. И, конечно же, ребенку на уроке должно быть интересно и понятно, зачем он изучает данный материал и где может применить полученные знания, независимо от того, в каком классе он обучается. Текст учебника математики отличается от других учебников еще и тем, что он насыщен формулировками. Дети с большим трудом запоминают формулировки теорем, правил и алгоритмов выполнения того или иного действия, они их не учат дословно, упуская порой важные слова или искажая смысл. Из-за этого у ребенка возникает неверное ощущение, что он все выучил хорошо, верно привел формулировку. Итак, важнейшее обще учебное действие – это смысловое чтение: извлечение информации; определение основной и второстепенной информации; построение речевых высказываний, адекватно, осознанно и произвольно передающих содержание текста, дающих ответ на вопрос; логические действия, направленные на анализ, обобщение, классификацию, рассуждения и умозаключения на основе прочитанного текста. Примеры приёмов работы с текстом, которые я использовала на своем уроке по теме «Преобразования выражений, содержащих арифметические квадратные корни» Приём «Преобразование и интерпретация информации» Этот способ формирует структурировать и систематизировать материал.Преобразовывать текст, используя новые формы представления информации: формулы, графики, диаграммы, таблицы, переходить от одного представления данных к другому; Учащиеся должны подготовить универсальную шпаргалку — опорный сигнал чтобы, посмотрев на нее, можно было найти ответы на все вопросы по данной теме. Приём «Верные и неверные утверждения» Этот приём формирует умение анализировать информацию, умение оценивать факты, умение отражать своё мнение. Этот приём используется как на этапе формирования новых знаний, так и при систематизации знаний. Учащиеся выражают своё отношение к ряду утверждений по правилу: верно - «+», неверно - « - ». Квадратным корнем из числа a называют число, квадрат которого равен а; Арифметическим квадратным корнем из числа а называют отрицательное число, квадрат которого равен а; Знак  называют знаком квадратного корня или радикалом; называют знаком квадратного корня или радикалом;Выражение, стоящее под знаком модуля, называют подкоренным выражением; Подкоренное выражение может принимать только отрицательные значения; Действие нахождения арифметического квадратного корня из числа называют извлечением квадратного корня; Уравнение х2 = а при а  0 имеет один корень; 0 имеет один корень;Уравнение х2 = а при а  0 имеет два корней; 0 имеет два корней;Уравнение х2 = а при а=0 не имеет корень; Для любого действительного числа а выполняется равенство  = =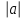 ; ;Для любого действительного числа а и любого натурального числа n выполняется равенство  = =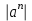 ; ;Для любых действительных чисел a и b таких, что а  0 и b 0 и b 0, выполняется равенство 0, выполняется равенство  = =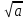   ; ;Для любых действительных чисел a и b таких, что а  0 и b 0 и b 0, выполняется равенство 0, выполняется равенство 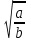 = = ; ;Тождественные преобразования выражений, содержащих арифметические квадратные корни: вынесение множителя из-под знака корня, внесение множителя под знак корня, освобождение от иррациональности в знаменателе дроби. Приём «Проверка навыков смыслового чтения» Задания «на соотнесение» - нахождение соответствия между формулами, выражениями, утверждениями, схемами, таблицами; Установите соответствие:
Таким образом, данные приёмы мне помогают развивать логическое мышление, мотивировать учащихся не только для работы на уроке, но и формировать представление о математической науке как сфере человеческой деятельности, о её значимости для развития цивилизации. |

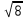 – b)(
– b)(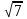 )(d +
)(d +  – х)(
– х)(