Венгерский метод. Содержание введение 4 математическая постановка задачи 5 определение опорного плана 8
 Скачать 105.72 Kb.
|
ВЕНГЕРСКИЙ МЕТОД3.1. Теоретическая справкаОсновные положения: Существенным нулем матрицы С называется нуль, соответствующая коммуникация которого в плане Х положительна. Элементы матрицы С, находящиеся в выделенных строках и столбцах называются выделенными. Сам метод состоит из следующих этапов: предварительного этапа, на котором вычисляется начальный план; итерации, которая состоит из проверки оптимальности и 3-х этапов, которым предшествует разметка. Этапы: поисковый этап эквивалентных преобразований построение цепочки и коррекция плана Этапы а) б) могут повторяться не однократно и завершаются итерации этапом в). На предварительном этапе происходит построение начального плана и определение невязок. План не является опорным, как в методе потенциалов, за счет этого образуются невязки. 1) В каждом столбце матрицы С отыскивается минимальный элемент, который затем вычитается из всех элементов столбца. В результате проведения операции образуется матрица С'. 2) В каждой строке матрицы С' отыскивается минимальный элемент, который вычитается из всех элементов строки. 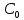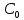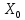В результате получается матрица  .3) Для нулей матрицы , двигаясь по столбцам, строится матрица  по известным правилам.4) Рассчитываются невязки по строкам и столбцам и суммарная невязка. По величине суммарной невязки можно весьма приблизительно определить число итераций до получения оптимального плана. Если получилось, что суммарная невязка равна нулю, то это говорит об оптимуме. Разметка: Разметка матрицы С выполняется перед началом итерации и действует до ее окончания. Каждой итерации соответствует новая разметка. На этапе разметки 1-ое: символом "+" отмечаются столбцы с нулевыми невязками. После этого столбцы считаются выделенными. 2-ое: Отмечаются верхней чертой нули матрицы С, соответствующие положительным элементам плана Х. Такие нули называются существенными нулями. Этапы: 1. Поисковый этап. В задачу поискового этапа входит нахождение в невыделенной части матрицы С нуля, находящегося на строке с положительной невязкой. Если 0 найден, то приступают к построению цепочки, в противном случае необходимо выполнить эквивалентные преобразования в матрице С. Матрица С просматривается по невыделенным столбцам. Найденный ноль отмечают штрихом. Если его невязка по строке оказывается положительной, то это говорит об успехе поиска, в противном случае строка отмечается плюсом и считается выделенной. Выделенная строка просматривается по выделенным столбцам, если на их пересечении окажется существенный ноль, то отмечают *, а знак выделения снимают, обводя в кружок, и пытаются продолжить поиск по столбцу со снятым выделением. В конце концов у нас либо найдется искомый ноль, либо все нули матрицы будут находиться в выделенных столбцах и строках. В этой ситуации необходимо будет перейти к этапу эквивалентных преобразований матрицы С. 2. Этап эквивалентных преобразований. В невыделенной части матрицы С отыскивается минимальный положительный элемент h, который затем прибавляется к выделенным столбцам и вычитается из невыделенных строк. В невыделенной части матрицы образуется хотя бы один ноль. 3. Построение цепочки. Цепочка содержит нечетное число элементов и в принципе может состоять из одного элемента. Построение начинается от последнего найденного нуля со штрихом по столбцу до нуля со звездой, далее по строке от нуля со звездой до нуля со штрихом. После того, как цепочка построена, производят коррекцию плана Х. Выбирается минимальный элемент невязки, строки начала, невязки столбца конца цепочки и элементов плана Х, соответствующих нулям со * в цепочке. Полученный элемент прибавляется ко всем элементам цепочки, которые стоят на местах, соответствующих нулям со штрихом и вычитаются из элементов цепочки, соответствующих нулям со *. Элементы плана Х не вовлеченные в цепочку не меняются Теоремы и информацию о опорных планах и венгерском методе можно найти в [3]. 3.2. Постановка и решение задачиРассмотрим метод потенциалов на примере. Пример. Решить транспортную задачу, заданную в табл. 3.1. венгерским методом: Таблица 3.1. Данные примера
Проверим условие баланса: 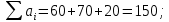 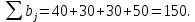 Условие баланса выполнено. Рассмотрим матрицу C: 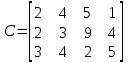 В матрице С в каждом столбце ищем минимальный элемент и вычитаем его из остальных элементов данного столбца. И получаем матрицу C’. 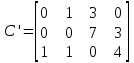 В матрице С’ в каждой строке ищем минимальный элемент и вычитаем его из остальных элементов данной строки. И получаем матрицу 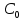 . 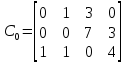Для нулевых элементов С0, перемещаясь по столбцам, строим матрицу Х0, корректируя элементы векторов А и В по мере её заполнения: Таблица 3.2. Промежуточные результаты
Ход заполнения x[1,2] = min{a2.b1}=b1=40, x[2,2] = min{a2.b2}=b2=30, x[3,3] = min{a3.b3}=a3=20, x[3,4] = min{a1.b4}=b4=50. 1-ая итерация. Этап разметки. Отмечаем символом "+" 1-й, 2-й и 4-й столбцы матрицы С0, а символом "" сверху нули этой матрицы, соответствующие ненулевым элементам плана Х0, которые являются существенными. 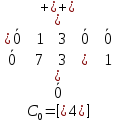 Поисковый этап. В невыделенной части матрицы С0, т.е. в 3-ем столбце и отмечаем невыделенный нуль С[3,3] апострофом Его невязка по строке нулевая. Строку выделим символом «+». В 4-м столбце отмечаем невыделенный ноль С[1,4]. Его невязка по строке нулевая. Строку выделим символом «+».В первом столбце данной строки стоит существенный ноль ( 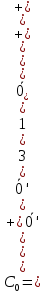 ), отмечаем его “”, а “+” этого столбца берем в «( )». В 1-м столбце так же находится невыделенный нуль, отмечаем его апострофом. Так как невязка по строке не равна нулю, строку не отмечаем. Этап построения цепочки и коррекции плана. Для коррекции плана выбираем корректирующий элемент  . Выбираем его из невязки строки начала цепочки и из невязки столбца конца цепочки. Коррекция плана: Прибавляем  к элементам  , которым в цепочке соответствовал элемент  , и отнимем от элементов , которым в цепочке соответствовал элемент  .Получаем новый план Х1. Таблица 3.3. Новый план
Так как суммарная невязка плана не равна 0 (≠0), то переходим ко второй итерации. 2-ая итерация. Этап эквивалентных преобразований. h=min{3;4}=3. Прибавим его к выделенным плюсом столбцам и отнимем от невыделенных строк, получим матрицу С1, в которую переносится вся индексация из С0. 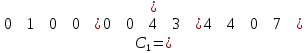 Этап разметки. Отмечаем символом "+" 1-й, 2-й и 4-й столбцы матрицы С0, а символом "" сверху нули этой матрицы, соответствующие ненулевым элементам плана Х1, которые являются существенными. 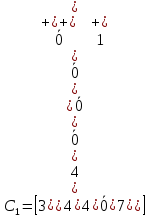 Поисковый этап. В невыделенной части матрицы С0, т.е. в 3-ем столбце и отмечаем нуль С[3,3] апострофом. В 3-ем столбце отмечаем невыделенный нуль С[1,3] апострофом Его невязка по строке нулевая. Строку выделим символом «+». В 1-й строке в 1-м столбце и в 4-м столбце отмечаем невыделенные нули С[1,1] и С[2,4]. В 1-м столбце 1-й строки стоит существенный ноль ( 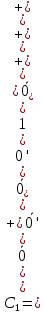), отмечаем его “”, а “+” этого столбца берем в «( )». Этап построения цепочки и коррекции плана. Для коррекции плана выбираем корректирующий элемент . Выбираем его из невязки строки начала цепочки и из невязки столбца конца цепочки. Коррекция плана: Прибавляем  к элементам , которым в цепочке соответствовал элемент , и отнимем от элементов , которым в цепочке соответствовал элемент .Получаем новый план Х2. Таблица 3.4. Новый план
Так как суммарная невязка плана равна 0 (≠0), следовательно, оптимальное решение получено. Переходим к расчету целевой функции. Для этого найдем сумму произведений ненулевых элементов плана Х2 на соответствующие им элементы исходной матрицы С: F=40*2+30*3+10*5+20*2+50*1=190. В результате решения был получен оптимальный план перевозок и найдено минимальное количество расходов необходимых для осуществления всех перевозок. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
