Содержание Задание на курсовую работу 2 Введение 4 Задания 5 Задание 1 5 Задание 2 8 Задание 3 12 Задание 4 14 Задание 5 17 Задание 6 21 Задание 7 23 Задание
 Скачать 237.33 Kb. Скачать 237.33 Kb.
|
Задание 3Опишем процесс помехоустойчивого кодирования, если используется код с проверкой на четность и составить структурную схему кодера. При передаче цифровых данных по каналу с шумом всегда существует вероятность того, что принятые данные будут содержать некоторый уровень частоты появления ошибок. Получатель, как правило, устанавливает некоторый уровень частоты появления ошибок, при превышении которого принятые данные использовать нельзя. Если частота ошибок в принимаемых данных превышает допустимый уровень, то можно использовать кодирование с исправлением ошибок, которое позволяет уменьшить частоту ошибок до приемлемой. Кодирование с обнаружением и исправлением ошибок, как правило, связано с понятием избыточности кода, что приводит в конечном итоге к снижению скорости передачи информационного потока по тракту связи. Избыточность заключается в том, что цифровые сообщения содержат дополнительные символы, обеспечивающие индивидуальность каждого кодового слова. Вторым свойством, связанным с помехоустойчивым кодированием является усреднение шума. Этот эффект заключается в том, что избыточные символы зависят от нескольких информационных символов. При увеличении длинны кодового блока (т.е. количества избыточных символов) доля ошибочных символов в блоке стремиться к средней частоте ошибок в канале. Обрабатывая символы блоками, а не одного за другим можно добиться снижения общей частоты ошибок и при фиксированной вероятности ошибки блока долю ошибок, которые нужно исправлять. Все известные в настоящее время коды могут быть разделены на две большие группы: блочные и непрерывные. Блочные коды характеризуются тем, что последовательность передаваемых символов разделена на блоки. Операции кодирования и декодирования в каждом блоке производится отдельно. Непрерывные коды характеризуются тем, что первичная последовательность символов, несущих информацию, непрерывно преобразуется по определенному закону в другую последовательность, содержащую избыточное число символов. При этом процессы кодирования и декодирования не требует деления кодовых символов на блоки. Разновидностями как блочных, так и непрерывных кодов являются разделимые (с возможностью выделения информационных и контрольных символов) и неразделимые коды. Наиболее многочисленным классом разделимых кодов составляют линейные коды. Их особенность состоит в том, что контрольные символы образуются как линейные комбинации информационных символов. Принцип обнаружения и исправления ошибок. Корректирующие коды строятся так, чтобы количество комбинаций М превышало число сообщений М0 источника. Однако в этом случае используется лишь М0 комбинаций источника из общего числа для передачи информации. Такие комбинации называются разрешенными, а остальные - запрещенными М-М0. Приемнику известны все разрешенные и запрещенные комбинации, поэтому, если при приеме некоторого разрешенного сообщения в результате ошибки это сообщение попадает в разряд запрещенных, то такая ошибка будет обнаружена, а при определенных условиях исправлена. Следует заметить, что при ошибке, приводящей к появлению другого разрешенного сигнала, такая ошибка не обнаружима. Расстоянием Хемминга d между двумя последовательностями называется число позиций, в которых две последовательности отличаются друг от друга. Наименьшее значение d для всех пар кодовых последовательностей называется кодовым расстоянием. Ошибка обнаруживается всегда, если её кратность, т.е. число искаженных символов в кодовой комбинации: g Исправление ошибок в процессе декодирования сводится к определению переданной комбинации по известной принятой. Расстояние между переданной разрешенной комбинацией и принятой запрещенной комбинацией d0 равно кратности ошибок g. Если ошибки в символах комбинации происходят независимо относительно друг друга, то вероятность искажения некоторых g символов в n-значной комбинации будет равна: Коды с обнаружением ошибок. Одним из кодов подобного типа является код с четным числом единиц. Каждая комбинация этого кода содержит помимо информационных символов - один контрольный, выбираемый равный 0 или 1 так, чтобы сумма количества единиц в комбинации всегда была четной. Простейшим примером кода с проверкой на четность является код Бодо, в котором к пятизначным комбинациям информационных символов добавляется шестой контрольный символ: 11001,1; 10001,0. Правило вычисления контрольного символа находится как: откуда вытекает, что для любой комбинации сумма всех символов по модулю два будет равна нулю. Это позволяет в декодирующем устройстве сравнительно просто производить обнаружение ошибок путем проверки на четность. Нарушение четности имеет место при появлении однократных, трехкратных и в общем случае нечетной кратности, что и дает возможность их обнаружить. Появление четных ошибок не изменяет четности суммы, поэтому такие ошибки не обнаруживаются. На рис. 3.1. показана структурная схема кодера. Характерной особенностью является наличие в цепи обратной связи решающее устройства, управляющего величиной шага квантования ∆b. Если знак приращений γ(k) остается неизменным в течение 3-4 интервалов дискретизации, то это означает наличие перегрузки. Решающее устройство удваивает амплитуду импульсов, поступающих на вход интегратора 1. Если в этом случае знак приращения (сигнал ошибки) не изменяется, то размер шага ∆b снова удваивается и т.д. При изменении знака приращения размер шага квантования уменьшается. Нетрудно понять, что, в состав устройства управления размером шага квантования должен входить анализатор плотности единиц и импульсный усилитель с управляемым коэффициентом усиления. На выходе интегратора 2 при изменении коэффициента усиления в зависимости от плотности единиц будет формироваться ступенчатое напряжение с адаптивно изменяющимся шагом квантования. 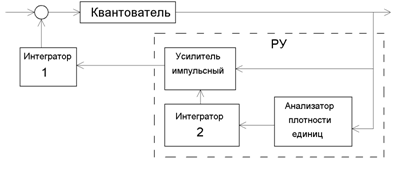 Рис. 3.1. Структурная схема кодера. |
