Содержание Задание на курсовую работу 2 Введение 4 Задания 5 Задание 1 5 Задание 2 8 Задание 3 12 Задание 4 14 Задание 5 17 Задание 6 21 Задание 7 23 Задание

• Название: Содержание Задание на курсовую работу 2 Введение 4 Задания 5 Задание 1 5 Задание 2 8 Задание 3 12 Задание 4 14 Задание 5 17 Задание 6 21 Задание 7 23 Задание
• Дата: 17.07.2022
• Размер: 237.33 Kb.
• Имя файла: 321657f.docx
• Тип: Реферат; #632422
• страница: 8 из 8

Задание 8

Определим величину параметра h2 на входе детектора, при которой достигается заданная вероятность ошибки Pош., если помеху, воздействующую на сигнал, считать "белым шумом" со спектральной плотностью мощности G0. Определим амплитуду сигнала, при которой достигается полученное значение h2.

Вероятность ошибки при оптимальном когерентном приёме равновероятных сигналов с ДАМ в канале с "белым" Гауссовским шумом, полученная в теории потенциальной помехоустойчивости, рассчитывается по формуле:

ош = 0,5 exp(-h2/2), (8.1)

где h2 = E/Go;

- энергия сигналов S1(t) и S0(t), (B2∙c);- спектральная плотность мощности помехи, (В2∙с) или (В2/Гц)

Отсюда:

= -2 ln(2 Pош). (8.2)= -2 ln(210-5) = 21,64
Для получения вероятности ошибки Pош =10-5, необходимо, чтобы величина h2 = 21,64

Мощность гармонического несущего сигнала:

= U2/2, (В2), (8.3)
где U - амплитуда сигнала, (B)

Энергия сигналов S1(t) и S0(t) равна:
Е = Рс TТАКТ, (B2∙c) (8.4)
Из формулы h2 = E/GO находим:

= h2 GO, (B2∙c) (8.5)

После подстановок и преобразований получим:
U = h2 GO/TТАКТ, (B) (8.6)
Или
U = h2 GO Fтакт, (B) (8.7)

U =  21,64 10-6 88 103 =2,69 (В)
Значение h2 = 21,64 достигается при амплитуде сигнала, равной U = 2,69 (В).

Задание 9

Вычислим вероятность неверного декодирования кодовой комбинации в декодере с учетом кодирования с проверкой на четность.

Кодовая комбинация, при условии использования кода с проверкой на четность, будет декодирована неверно, если будет принято с ошибкой четное количество символов.

Так как Pош<<1, то можно учитывать только вероятность ошибочного приёма двух элементов кодовой комбинации.

Тогда вероятность неверного декодирования кодовой комбинации, состоящей из n - элементов равна:
Рош К К = Р(2/n) = C2n P2ош  (1 - Рош )n-2 С2n P2ош (9.1)
где

Р(2/n) - вероятность двукратной ошибки в n- элементной кодовой комбинации;n - число сочетаний из n - элементов по 2 элемента ( показывает число возможных вариантов двукратной ошибки в n- элементной кодовой комбинации кода);

n = n!/ [2!  (n - 2)!] (9.1)

- длина кодовой комбинации помехоустойчивого кода.

ош К К n!/ [2!  (n - 2)!]  P2ош =11!/ [2!  (11-2)!]  (10-6) 2 =5510-12

Задание 10

Определим пропускную способность канала связи.

Для канала с постоянными параметрами, и единственной помехой в виде белого "Гауссовского" шума со спектральной плотностью мощности GO, полоса частот которого равна ширине спектра сигнала: FК = FС, пропускная способность (максимально возможная скорость передачи информации по каналу при заданных характеристиках сигналов и помех) рассчитывается по формуле Шеннона для непрерывного Гауссовского канала без памяти:

= FК log2 (1 + PC/ PШ), (бит/c) (10.1)
где FК - полоса частот канала, равная ширине спектра модулированного сигнала:
FК = FМОД . (10.2)
РС/ Pш - отношение сигнал /шум (мощностей сигнала и шума) на входе детектора.

Т.к. РС = Е/ТТАКТ = Е FТАКТ, а РШ = GO  FК = GO  FМОД и Е = h2 GO, то:

РС/ РШ = h2 FТАКТ/ FМОД . (10.3)
Для ДОФМ сигналов
FМОД = FК = FДОФМ =(2 3)∙FТАКТ

_{Получим} FМОД = FК = FДОФМ =2∙FТАКТ=2∙88∙103=176∙103(Гц)=176(кГц).

РС/ РШ = h2/2 = 21,64 /2=10,82

FК = FДОФМ = 176(кГц)

С = 176 103 ∙log2(1+10,82)=176 103 ∙3,563= 627,09∙103 (бит/c)=627,09(кбит/с)
При увеличении полосы частот канала FК до бесконечности, пропускная способность канала стремится к пределу, называемому потенциально возможной пропускной способностью канала (теорема Шеннона):

C = lim C = (PC/ GO) log2е, (бит/с). (10.4)

FК

Так как РС = Е FТАКТ = h2 GO FТАКТ, то C = h2 FТАКТ log2е, (бит/с).е=lge/lg2≈1,4329594 = 21,64 88 103 1,4329594 =2,73106(бит/c)=2,73(Мбит/с) /C = 2,73106/627,09∙103 = 4,35

Потенциальная возможность пропускной способности канала по теореме Шеннона в 4,35 раза превышает пропускную способность реального канала нашей системы связи. Эффективность использования пропускной способности канала при оптимальном некогерентном приёме помехоустойчивых ДМ сигналов достаточно высока.

Опишем взаимосвязь пропускной способности канала и его полосы пропускания.

Максимальную скорость, с которой канал способен передавать данные, называют пропускной способностью канала или битовой скоростью.

Найквист открыл взаимосвязь между пропускной способности канала и шириной его полосы пропускания.

Теорема Найквиста:

= 2H∙log2M (бит/с), (10.5)

где Vmax- максимальная скорость передачи, H - ширина полосы пропускания канала, выраженная в Гц, М - количество уровней сигнал, используемых при передаче. Например, из этой формулы следует, что канал с полосой 3 кГц не может передавать двухуровневые сигналы быстрее 6000 бит/с.

Эта теорема также показывает, что, например, бессмысленно сканировать линию чаще, чем удвоенная ширина полосы пропускания. Действительно, все частоты выше этой отсутствуют в сигнале, а поэтому вся информация, необходимая для восстановления сигнала будет собрана при таком сканировании.

Однако теорема Найквиста не учитывает шум в канале, который измеряется как отношение мощности полезного сигнала к мощности шума: S/N. Эта величина измеряется в децибелах: 10∙log10(S/N)(дБ). Например, если отношение S/N равно 10, то говорят о шуме в 10 Дб, если отношение равно 100, то 20 дБ.

На случай канала с шумом есть теорема Шеннона, по которой максимальная скорость передачи данных по каналу с шумом равна:

∙log2 (1+S/N) (бит/с) (10.6), где S/N - соотношение сигнал-шум в канале

Здесь уже не важно количество уровней в сигнале. Эта формула устанавливает теоретический предел, которой редко достигается на практике. Например, по каналу с полосой пропускания в 3000 Гц и уровнем шума 30Дб (это характеристики телефонной линии) нельзя передать данные быстрее, чем со скоростью 30000 (бит/с).

Нижеследующая теорема дает прямую наглядную интерпретацию ошибочности, показывая, кроме того, что это единственная подходящая мера.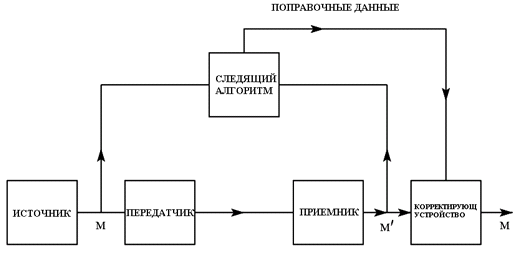


Рис. 10.1. Схематическое изображение корректирующей системы.
Теорема: Если пропускная способность корректирующего канала , можно закодировать корректирующую информацию таким образом, что ее можно послать по этому каналу и скорректировать все ошибки за исключением их произвольно малой доли . Это невозможно, если пропускная способность корректирующего канала меньше .

- количество дополнительной информации, необходимой приемнику для коррекции принятого сообщения. Для доказательства первой части рассмотрим длинные последовательности принятого сообщения и исходного сообщения . Есть логарифмически большое число сообщений M, которые могли бы привести к принятому сообщению . Таким образом, необходимо передавать двоичных цифр каждые T секунд. Это может быть сделано при частоте ошибок в канале с пропускной способностью . Второе утверждение может быть доказано, если для доказательства второго утверждения заметим, что для любых дискретных случайных величин x, y, z.
(10.7)
Левую часть можно преобразовать
(10.8) (10.9)
Если мы отождествим x с информацией, выдаваемой источником, y- принятым сигналом, и z- сигналом, передаваемым по корректирующему каналу, то правая часть является разностью ошибочности и темпа передачи по корректирующему каналу. Если этот темп меньше ошибочности, то правая часть будет больше нуля, и . А эта величина характеризует неопределенность сообщения при известных принятом и корректирующем сигналах. Когда она больше нуля, частота ошибок не может быть сделана произвольно малой.

Основная теорема для дискретного канала с шумом.

Можно передать по каналу информацию с темпом C произвольно малой частотой ошибок или же ошибочностью путем соответствующего кодирования. При попытке же передачи с большим темпом неизбежно будет некоторая ошибочность. Мы не сможем передать информацию с темпом, большим C.

Данная ситуация иллюстрируется рис. 10.2. Темп поступления информации в канал отложен по горизонтальной оси, а ошибочность - по вертикальной.

Все точки выше жирной линии в заштрихованной области достижимы, все точки ниже - недостижимы. Точки на линии в общем случае недостижимы, за исключением двух, которые обычно могут быть достигнуты.

Теорема: Пусть дискретный канал имеет пропускную способность C, а источник - энтропию в секунду H. При существует такая система кодирования, что информация от источника может быть передана по каналу с произвольно малой вероятностью ошибки.

При H>C возможно так закодировать информацию, что ошибочность будет меньше H-C+ε, где ε произвольно мало.

Не существует способа кодирования, дающего ошибочность меньше H-C.


Рис. 10.2 Допустимая ошибочность для заданной энтропии на входе канала.
Для дискретных каналов без помех К. Шенноном была доказана следующая теорема: если производительность источника , то существует способ кодирования и декодирования, при котором вероятность ошибочного декодирования и надежность могут быть сколь угодно малы. Если же , то таких способов не существует.

Заключение

Передача сообщений из одного пункта в другой составляет основную задачу теории и техники связи.

Система связи - совокупность средств и среды распространения сигналов, обеспечивающих передачу некоторых сведений, или информации, от источника к потребителю.

Если посмотреть прохождение сигнала по каналу связи, в который входит источник сигнала, АЦП, модулятор, линия связи, демодулятор. ЦАП, потребитель, то наиболее низкой помехозащищенностью обладает линия связи. Линия связи может представлять собой различные среды передачи сигнала, например, для передачи электрического сигнала используют проводную линию, для передачи радио сигнала используют радиосвязь (начиная с простейшего радиоприемника и заканчивая сложной спутниковой связью), для передачи светового сигнала используют волоконно-оптическую линию связи.

При передаче сигнала по линии связи на него воздействует, в основном, низкочастотный, случайный во времени шум, который является результатом деятельности человека (трение щеток электромотора, искрение замыкающихся и размыкающихся контактов, искрение контактной сети электровоза, взаимное влияние различных видов связи), а также природных явлений (атмосферные влияния, космические радиоизлучения), и в теории связи мы пытаемся избавиться от этих шумов путем повышения помехоустойчивости канала.

Путями повышения помехоустойчивости являются: модуляция сигнала, кодирование сигнала с применением дополнительной проверки пришедшего сигнала с помощью проверочных символов, различные виды приема сигналов, повышение рабочей частоты канала.

Как уже было сказано выше, на сигнал воздействует низкочастотный шум, поэтому стараются уйти в область высоких частот. Для этого используют в качестве несущей частоты - высокочастотный сигнал. Процесс наложения низкочастотного сигнала на высокочастотный сигнал называется модуляцией.

Рассматривая различные виды модуляции, можно выделить АМ. ЧМ и ФМ. Наиболее простая и дешевая модуляция - амплитудная, однако она обладает самой низкой помехозащищенностью. Ее обычно применяют там, где безошибочный прием не очень стужен. Далее следует частотная модуляция. Этот вид модуляции обладает более повышенной помехоустойчивостью, но он и сложней в реализации. И, наконец, последний вид модуляции - ФМ. Он обеспечивает наибольшую помехозащищенность, однако, этот вид самый сложный в реализации.

Модуляция также обеспечивает наименьшие габариты антенны, минимальную мощность передатчика, дает возможность введения многоканальной связи. Если говорить о кодировании, то это позволяет автоматизировать процесс, повысить помехоустойчивость, однако это может привести к нежелательным последствиям, таким как, например, расширение спектра.

Список источников и литературы

Используемая литература

1. 
   Баскаков С.И. "Радиотехнические цепи и сигналы". Учебник для вузов. М.: "Высшая школа", 2005 г.
   
2. 
   Гоноровский И.С. "Радиотехнические цепи и сигналы". Учебник для вузов. М.: "Советское радио", 1971 г.
   
3. 
   Гоноровский И.С. "Радиотехнические цепи и сигналы. Примеры и задачи". Учебное пособие для вузов. М.: "Радио и связь", 1989 г.
   
4. 
   Методические указания к выполнению курсовой работы.
   
5. 
   Кловский Д.Д. "Теория передачи сигналов". - М.: "Связь", 1973 г.
   
6. 
   Кловский Д.Д., Шилкин В.А. "Теория электрической связи". Сборник задач и упражнений. М.: "Радио и связь", 1990.
   

Используемые программы

1. 
   Microsoft Word
   
2. 
   Math Cad
   
3. 
   Компас 5.11