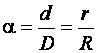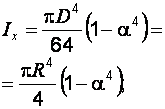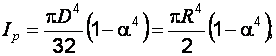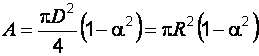Сопротивление материалов
 Скачать 1.21 Mb. Скачать 1.21 Mb.
|
|
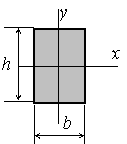
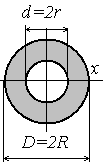
Сопротивление материалов – это наука о методах расчёта элементов инженерных конструкций на прочность, жёсткость, устойчивость. Утверждение, что напряжения и перемещения в сечениях, удалённых от места приложения внешних сил, не зависит от способа приложения нагрузки, называется принципом Сан-Венана. Тело, один размер которого намного превышает два других, называется стержнем или брус. Силы взаимодействия между частями рассматриваемого тела называются внутренними. Полное напряжение в точке сечения, в общем случае, раскладывается на нормальное и касательное напряжение. Распределение нормальных напряжений при растяжении – сжатии вдали от мест нагружения, резкого изменения формы и размеров поперечного сечения существенно зависит от величины приложенных внешних сил. Абсолютное удлинение. Коэффициентом Пуассона называется отношение относительной поперечной деформации к относительной продольной деформации, взятое по абсолютной величине. К стержню квадратного поперечного сечения предложена одинаковые растягивающие силы. Если одновременно увеличить в два раза длину стержня и размер стороны, абсолютное удлинение стержня уменьшится в два раза. Какие деформации называются упругими? это если восстанавливается первоначальная форма после прекращения действия сил приведших. Какие деформации называются остаточными (пластическими)? Это сохранение деформированной формы после прекращения этих же сил, приведших к деформации. В чем заключается метод сечения? Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки. Точка D соответствует приделу прочности. 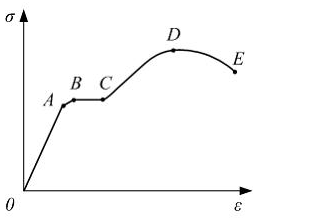  http://sopromato.ru/rastyazhenie-i-szhatie/uslovie-prochnosti-zhestkosti-dopuskaemoe-napryazhenie.html http://sopromato.ru/rastyazhenie-i-szhatie/uslovie-prochnosti-zhestkosti-dopuskaemoe-napryazhenie.html Диаметры d1 и d2(мм) равны 20,4 и 21,85. .  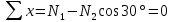 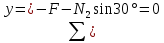 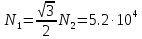 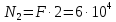 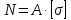 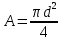 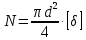 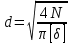 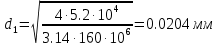 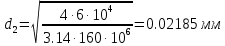 Продольные линейные деформации на участке СК равна: 2F\EA  Дано: Е,А,а,F Найти: 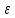 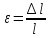 ; ; 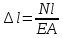 ; ; 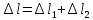 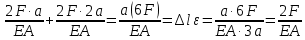 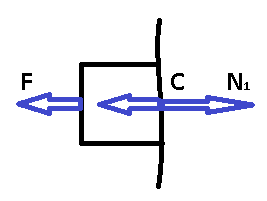 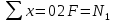  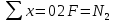 Как сформулировать закон Гука? Зако́н Гу́ка — утверждение, согласно которому деформация, возникающая в упругом теле (пружине, стержне, консоли, балке и т. п.), пропорциональна приложенной к этому телу силе. Что Называется коэффициентом поперечной деформации? Коэффициентом поперечной деформации, или коэффициентом Пуассона, представляет собой отношение относительной поперечной деформации к продольной, взятое по абсолютной величине. Коэффициент Пуассона наряду с модулем упругости Е характеризует упругие свойства материала. Что называется приделом пропорциональности, приделом упругости, приделом текучести, приделом прочности? Для придела пропорциональности справедлив закон Гука: относитель. удлинение прямо пропорционально норм. напряжению; придел текучести: после достижения придела пропорциональности деформация растет быстрее напряжения, достигнув величины текучести деформация растет без увеличения напряжения; Придел прочности: напряжение повышается после площадки текучести до наивысшей точки, наибольшее напряжение выдерживаемое образцом. Допустимый размер поперечного сечения стержня из условия жесткости равен: 22,36см. Для стержня круглого поперечного сечения наименьший размер D из условия прочности равен: 10см. 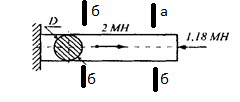  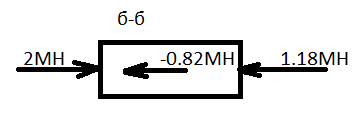 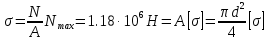 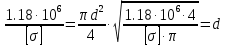 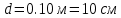 В чем разница между пластичным и хрупкими материалами? Основная разница между хрупкими и пластичными материалами заключается в том, что хрупкие материалы разрушаются при очень небольших деформациях, в то время как окончательное разрушение пластичных материалов происходит лишь после значительных изменений формы. Образцы из хрупких материалов ( например, из серого чугуна) разрушаются при весьма малых деформациях, а из пластичных материалов ( например, из малоуглеродистой стали) - при значительных деформациях. Что называется коэффициентом запаса прочности? Отношение' предельного напряжения о к наибольшему расчетному напряжению а, возникающему в элементе конструкции при эксплуатационной нагрузке, обозначают буквой и называют коэффициентом запаса прочности. Показывают во сколько раз нагрузка больше допустимого усилия. Как формируются условия прочности при любом виде деформации? Тут формула! Что такое жесткость с поперечного сечения? АЕ из закона Гука. Что характеризует величина Е? Модуль продольной упругости. Величина площади среза равна: 2Пd*2/4.  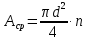 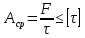 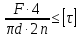 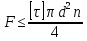 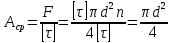 Что называется абсолютной и относительной сдвигом? Каждая из граней параллелепипеда при деформации частичного сдвига перемещается относительно противоположной грани на величину называемую абсолютным сдвигом; Отношения абсолютно сдвига к расстоянию между противоположным и гранями называется относительным сдвигом. Как формулируется закон Гука при сдвиге? Смотреть в учебнике на стр 124. Какова формула связи в трех упругих констант? Смотреть в учебнике на срт 127. Минимальная высота головки болта равна: F/Пd[ср]. При кручении максимальное касательное напряжение возникает в точке: в точке D. 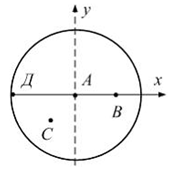 Наименьший допускаемые диаметр вала равен: 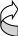    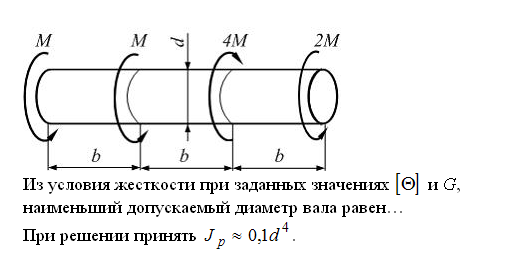                        1 1    2 2Дано: 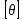 ,G, ,G, 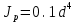 Найти: d-? Найти: d-?Решени: 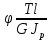 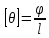 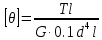 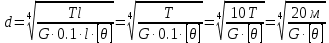 Эпюра распределения касательных напряжений в поперечном сечение трубы имеет вид: 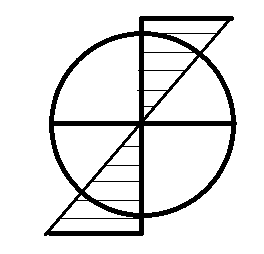 При деформации кручения угол взаимного поворота двух сечений, отнесённых к расстоянию между ними называется: Относительным углом закручивания. Тогда максимальный относительный угол закручивания равен: 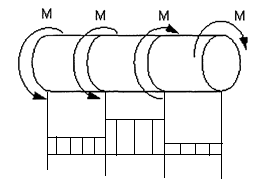 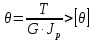 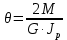 Максимальное значение относительного угла закручивания равно: 3M/GJp.  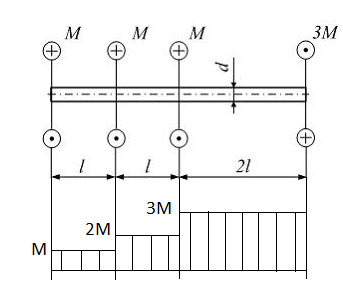  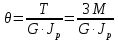 Из-за расчёта на жёсткость максимально допустимое значение параметров внешней нагрузки М равно:  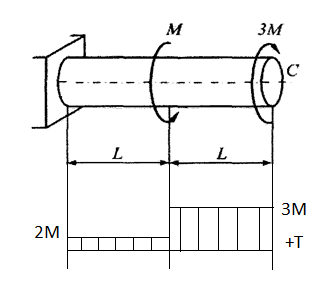 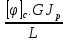 Правила построения эпюр крутящих моментов?Зная величины внешних скручивающих моментов и используя метод сечений, мы можем определить крутящие моменты, возникающие в поперечных сечениях вала. Крутящий момент Мк в сечении вала числено равен алгебраической сумме внешних скручивающих моментов, действующих по одну сторону от сечения, при этом могут рассматриваться как левая, так и правая отсеченные части вала.Примем правило знаков для крутящего момента:Крутящий момент считается положительным, если при взгляде в торец отсечены части бруса действующей на него момент представляется направленным по движению часовой стрелки. Какие напряжения возникают в поперечном сечении кругового стержня при кручении и как они направлены? В вале возникают условия чистого сдвига, в поперечных сечениях действуют только касательные напряжения, нормальные напряжения равны нулю.Направление которых в каждой точке перпендикулярно радиусу, соединяющего эту точку с центром сечения, а значение прямо пропорционально расстоянию точки от центра Чему равен полярный момент инерции кругового сечения? 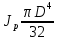 Что называется моментом сопротивления при кручении? Wp - Момент вызывающий деформацию кручения. Максимальный относительный угол закручивания имеет место на участке: 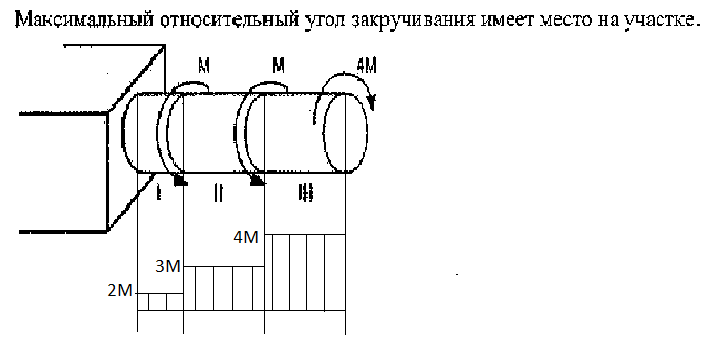 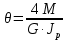 Условия прочности для стержня имеют вид: 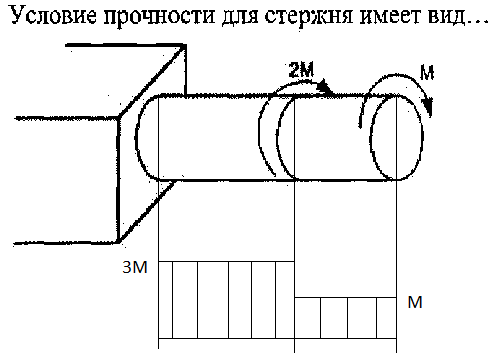 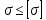 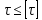 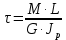 Коэффициент запаса прочности равен: ???  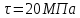 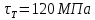 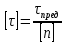 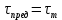 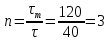 Что называется полным и относительным углом закручивания бруса? Полный угол: поворот бруса относительно её центральной оси под действием моментов. Относительная угол: Отношения полного угла закручивания к длине U=dY/dx. Как производят расчёт вала на прочность? 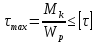 Как производят расчёт вала на жёсткость 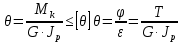 Статический момент площади сечения относительно оси х равен 72а*3 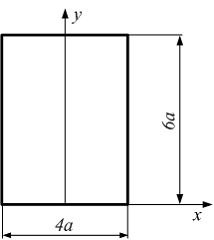 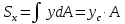 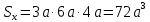 Осевой момент инерции площади сечения относительно оси равен b*4/6 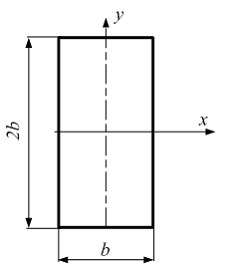 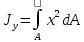 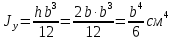 Осевой момент инерции относительно оси равен 2440  Для сечения известны осевые моменты инерции сечения относительно осей , , : 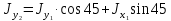 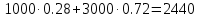 Что такое Sx, Jx, Jp, Jxy и их единицы измерения? Осевой, Полярный, Центробежный момент инерции (см*4). Чему равен статический момент сечения относительно оси, проходящей через центр его тяжести? Равен О. Формула для определения осевых моментов инерции относительно центральных осей круга, прямоугольника, кольца?  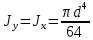
Если в плоскости сечения несколько параллельных осей, относительно какой из них Jx равен минимальному значению? Относительно которых главная ось принимает min значение. Что такое главные моменты инерции? Момент инерции относительно главных осей. Осевой момент инерции сечения относительно оси X равен: 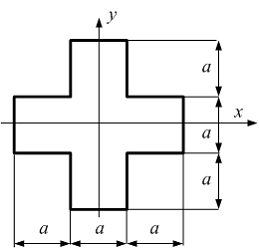 Осевой момент инерции сечения относительно оси равен 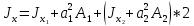 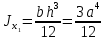 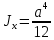 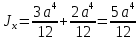 Осевой момент инерции сечения относительно оси X1 равен: 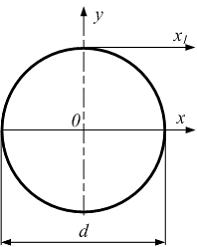 Осевой момент инерции сечения относительно оси равен 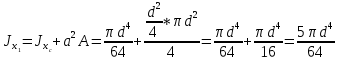 Из указанных центральных осей главными осями сечения являются: Х1,Х2,Х3,Х4. 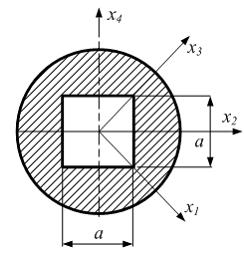 Момент инерции сечения относительно оси равен… 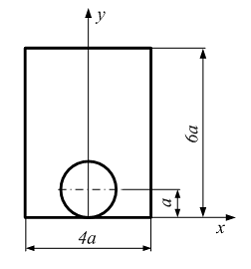 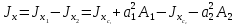 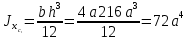 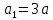 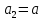 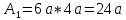 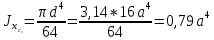 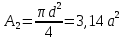 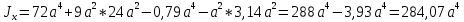 Координата центра тяжести Yc фигуры равна  Координата центра тяжести фигуры равна… Координата центра тяжести фигуры равна…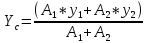 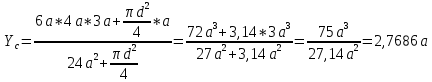 Из указанных центральных осей сечения равнобокого уголка главными являются: Х2. 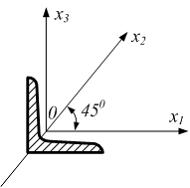 Из указанных центральных осей сечения равнобокого уголка главными являются…. X2 Какие оси называются главными и главными центральными осями инерции? Оси относительно которых моменты инерции принимают экстремальное значение называются главными осями. Главное оси проходящие через центр тяжести называются центрами осями. Чему равен Jxy относительно главных осей инерции? Равен 0. В каких случаях без вычисления можно установить положение главных осей инерции сечения? Когда фигура симметрична. Если Jx=Jy и Jxy=0, то какие оси сечения являются главными? То центральные оси являются главными. Ось относительно которой статический момент площади сечения равен нулю называются? Центральная ось. На рисунке размеры поперечного сечения заданы в см. Осевой момент инерции сечения относительно центральной оси Х равен 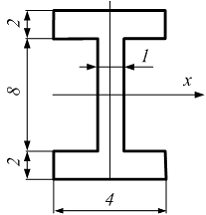 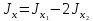 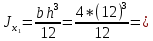 14*144=576 b=4 h=16 14*144=576 b=4 h=16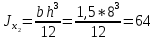 b= b=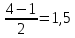 h=8 h=8 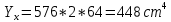 Если h=3b, то значение осевого момента инерции площади 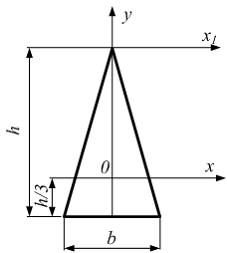 Если , то значение осевого момента инерции площади 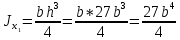 Статический момент площади сечения относительно оси Х равен 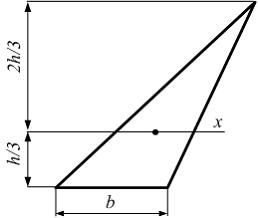 Статический момент площади сечения относительно оси x равен…0 Поперечное сечение балки составлено из вертикального листа и четырех неравнобоких уголков 80х50х5. Характеристики уголка заданы. Размеры на рисунке даны в мм. Моменты инерции сечения Jx и Jy соответственно равны: Статический момент площади сечения относительно оси Х равен 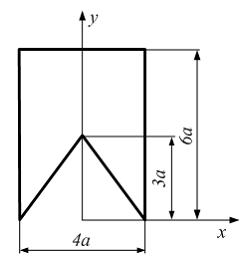 Статический момент площади сечения относительно оси x равен… 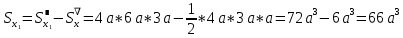 Осевой момент инерции сечения относительно оси Х1 равен  Осевой момент инерции сечения относительно оси равен… 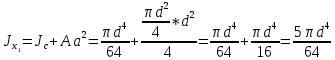 Момент инерции площади фигуры относительно оси Х, проходящей через центр тяжести фигуры равен 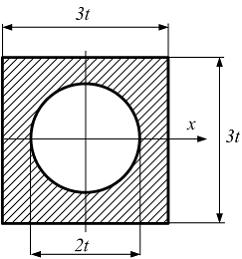 Момент инерции площади фигуры относительно оси x, проходящей через центр тяжести фигуры, равен … 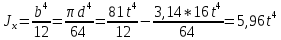 Поперечное сечение балки составлено из двух швеллеров 20 и листов прикреплённых с помощью сварки. Характеристики швеллера приведены. Размеры на рисунке даны в мм. Осевой момент инерции сечения относительно главной центральной оси Х равен: Зависимость между компонентами напряженного и деформированного состояния в пределах малых упругих деформаций носит название? Обобщенного закона Гука. Правило согласно которому на взаимно перпендикулярных площадках элемента выделенного из тела касательные напряжения равны по величине и направлены к общему ребру или от него называют? Закон парности касательных напряжений. Напряженное состояние чистый сдвиг показано на рисунке: 3. Чистый сдвиг 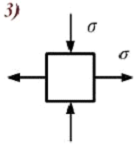 Оси относительно которых центробежный момент инерции равен нулю ,а осевые моменты принимают экстремальные значения ,называются: Главными осями. 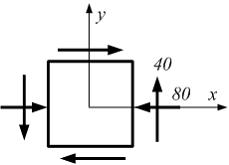 На гранях элементарного объема (см. рисунок) определены значения напряжений в МПа. Угол между положительным направлением оси x и внешней нормалью к главной площадке, на которой действует минимальное главное напряжение, равен … 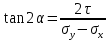 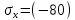 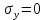 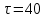 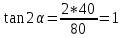 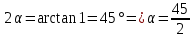 =22,5 =22,5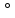 На гранях элементарного объёма определены значения напряжений в МПа. Угол между положительным направлением оси Х и внешней нормалью к главной площадке, на которой действует мин главное напряжение, равно??? Какие имеются виды напряженного состояния материала? Линейное, плоское, объемное. Объемный элемент находится под действием нормальных напряжений показанных на рисунке: бх=50МПа, ...... 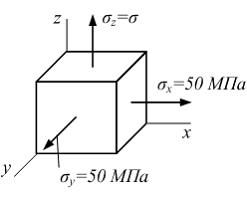 Объемный элемент находится под действием нормальных напряжений, показанных на рисунке: 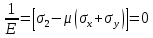 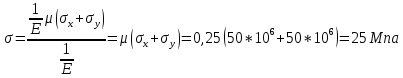 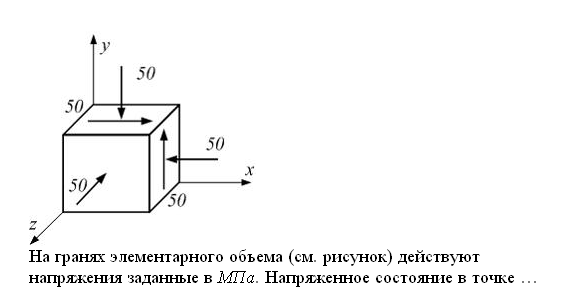 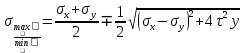 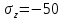 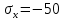 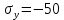 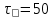 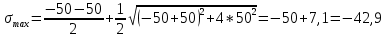 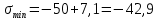 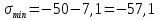 Изотопный материал на растяжение и сжатие работает неодинаково. Для оценки прочности материала при сложно напряженном состоянии используется теория? Напряженного состояния. Площадки в исследуемой точке напряженного тела на которых касательные напряжения равны нулю называют: Напряженными состояниями в точке. Напряженное состояние при значениях б=0МПа, б2=-20МПа, б3=-50МПа называют: Плоским или двуосным. Три взаимно перпендикулярные оси в системе которых отсутствуют угловые деформации называют: Главными осями деформационного состояния. Совокупность линейных и угловых деформаций возникающих по различным осям и в различных плоскостях проходящих через данную точку тела называют: Деформированное состояние в точке. Модуль упругости материала Е и коэффициент Пуассона заданы. Относительное изменение объема равно 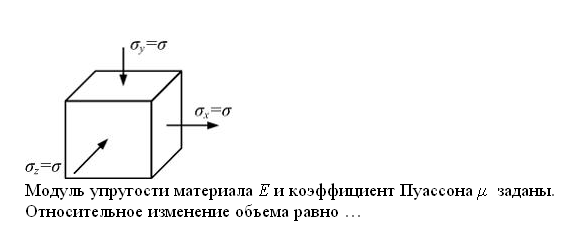 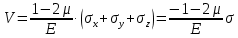 Главные напряжения для напряженного состояния показанного на рисунке равны: 1=150 МПа, 2=50 МПа, 3=0 МПа; Одна грань элемента свободна от касательных напряжений. Поэтому это главная площадка, а нормаль-ное напряжение главное напряжение на этой площадке также равно нулю. Зависимость между компонентами напряженного и деформированного состояния в пределах малых упругих деформаций носит название: Обобщенного закона Гука. Согласно теории наибольших касательных напряжений (третья теория прочности) самое опасное напряженное состояние показано на рисунке: Наибольшая величина эквивалентного напряжения получается для напряженного состояния показанного на рисунке Б по этому данное напряженное состояние является самым опасным. Тип напряженного состояния показанного на рисунке называется: Линейным. Чему равно наибольшее касательное напряжение в случае плоского напряженного состояния Наибольшее и наименьшее касательные напряжения
Эти напряжения действуют на площадках, расположенных под углом 45° к первой и второй главным площадкам. Если главные напряжения σ1 и σ2 имеют одинаковый знак, то наибольшее касательное напряжение действует на площадке, расположенной под углом 45° к плоскости напряжений (плоскости ху). В этом случае: Что представляют собой площадки сдвига и как они наклонены главным площадкам? Касательные напряжения действующее по боковым граням рассматриваемого параллелепипеда являются экстремальными эти грани являются площадками сдвига Площадки чистого сдвига наклонены по отношению к главным площадкам под углом 45 Проверка на прочность по касательным напряжениям необходимо в случае если: Короткие балки нагружены перпендикулярно продольной оси силами, имеющими большое значение; материал балки плохо сопротивляется сдвиговым деформациям; ширина поперечного сечения балки в районе нейтральной оси мала. Эпюра изгибающих моментов имеет вид 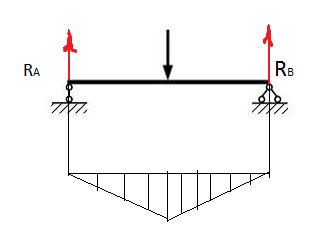 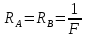 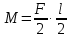 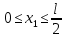 Балка нагружена равномерно распределённой нагрузкой интенсивностью q. Эпюра изгибающих моментов имеет вид: 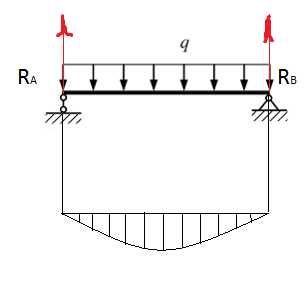 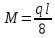 Вывод формулы для определения нормальных напряжений при чистом сгибе основывается на: Гипотезе плоских сечений и гипотезе об отсутствии взаимного надавливания продольных слоев балки.  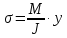 Прямоугольная балка имеет два варианта расположения поперечного сечения. Отношение наибольших нормальных напряжений для этих двух вариантов равно 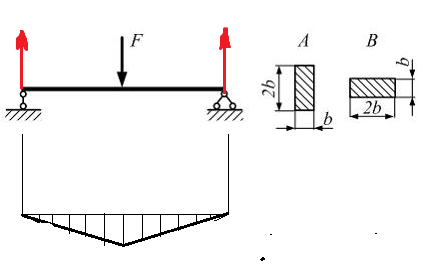 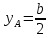 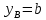 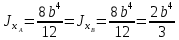 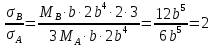 Консольная балка нагружена, как показано на схеме. Материал балки одинаково работает на растяжение и сжатие. Допускаемое напряжение , размеры b и l заданы. Из расчета по допускаемым напряжениям значение силы 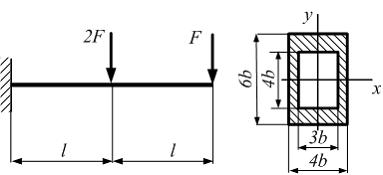 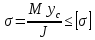 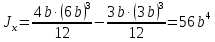 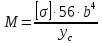 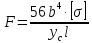 Стальная балка имеет два варианта расположения квадратного поперечного сечения. В первом случае она нагружается параллельно стороне квадрата. Во втором – в диагональной плоскости. Отношение прогибов равно 1 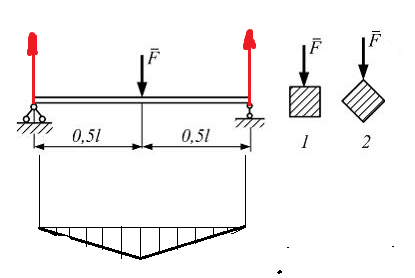  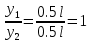 В опасном сечении балки, выполненной из пластичного материала (допустимое напряжение [б]=160МПа), значение изгибающего момента. Отношение массы балки прямоугольного сечения (с отношением сторон h/b=2) к массе балки двутаврого сечения равно: 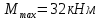 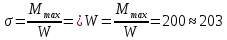 Полная проверка прочности балки при изгибе включает в себя: Проверку по нормальным напряжениям и проверку по главным напряжениям. Прогиб на свободном конце балки . Угол поворота поперечного сечения над опорой равен 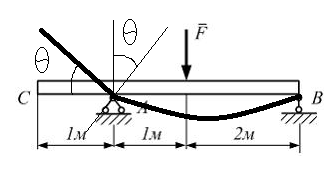 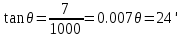 Поперечная сила Qy в произвольном поперечном сечение стержня численно равна алгебраической сумме проекции на ось: Из всех внешних сил расположенных по одну сторону от рассматриваемого сечения. При полном поперечном изгибе нормальные напряжения по ширине сечения балки: Распределяется равномерно. Консольная балка на участке АВ нагружена равномерно распределенной нагрузкой интенсивности q. Жесткость поперечного сечения стержня на изгиб EIz всей длине постоянна. Угол поворота сечения B, по абсолютной величине равен… 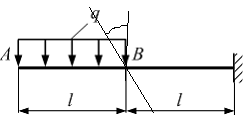 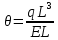 Жесткость поперечного сечения на изгиб по длине балки постоянна. Размер задан. Значение силы F , при которой прогиб концевого сечения В будет f, равно … 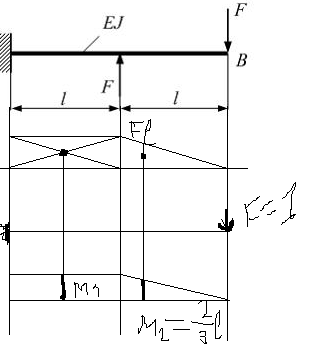 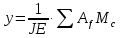 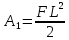 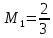 L L 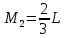 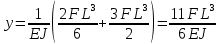 F= 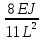 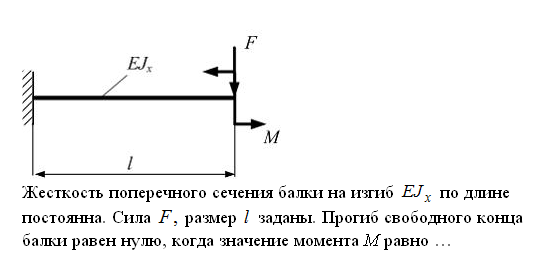 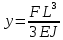 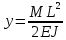 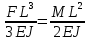 3M=F 3M=F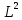 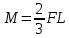  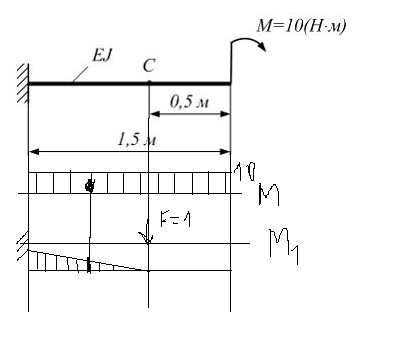 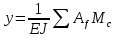 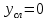 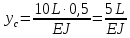  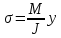 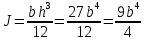 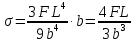 Определить угол поворота сечения балки над левой опорой 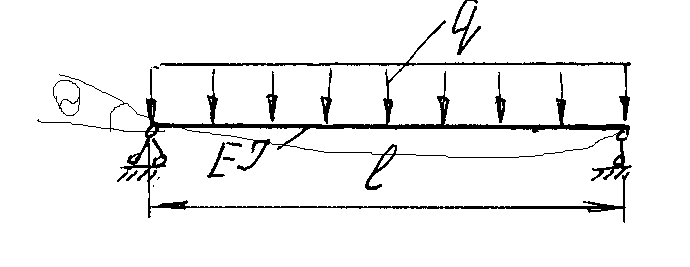 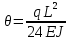 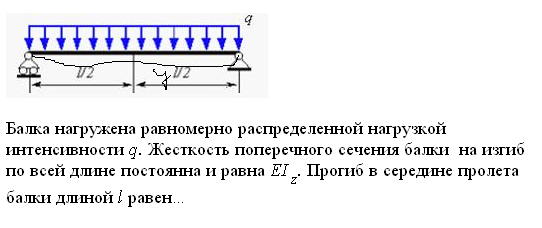 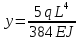 Определить стрелу прогиба балки 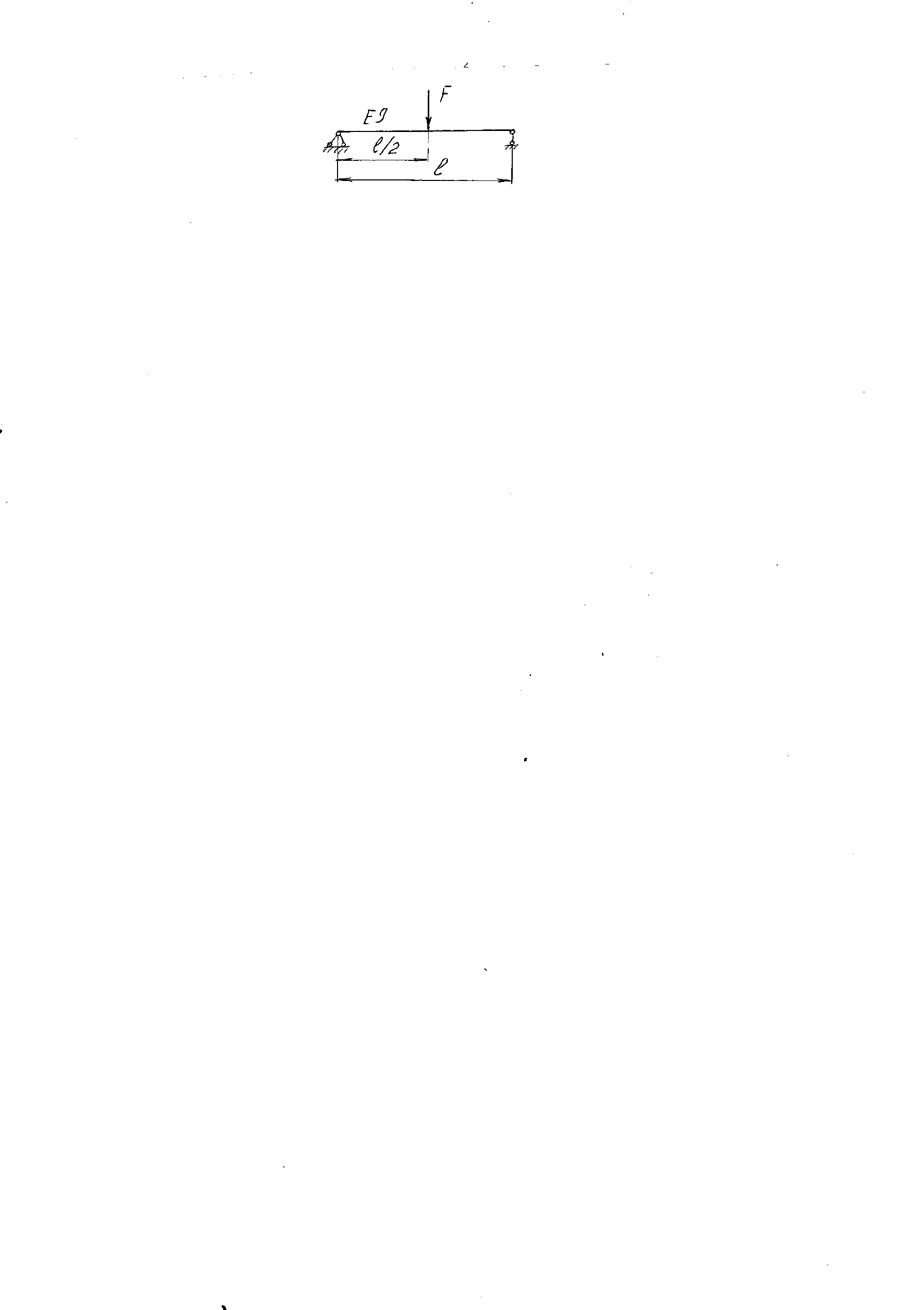 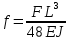 Определить угол поворота сечения балки над левой опорой 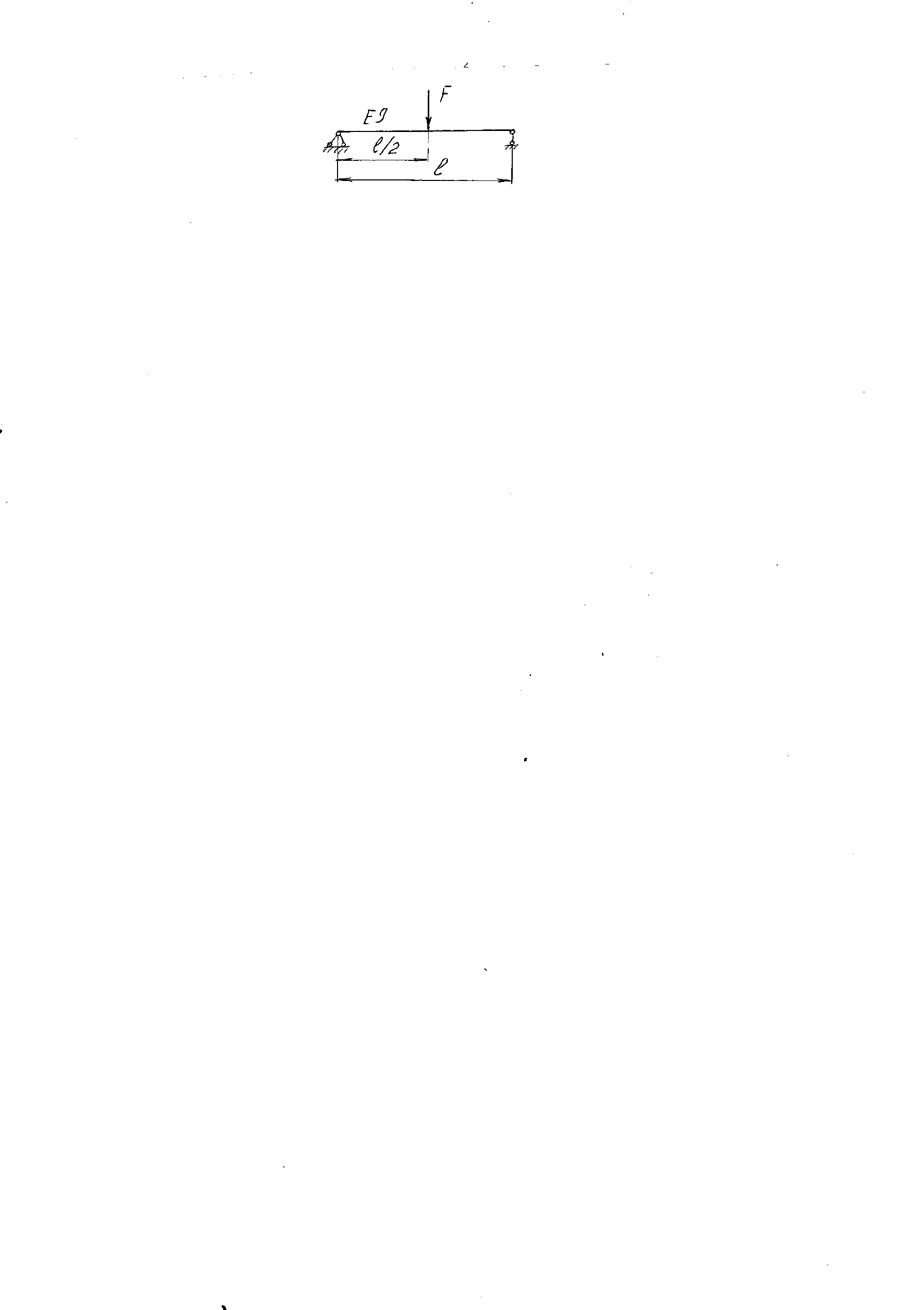 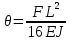 Определить прогиб концевого сечения балки  y= 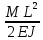 Определить угол поворота концевого сечения балки 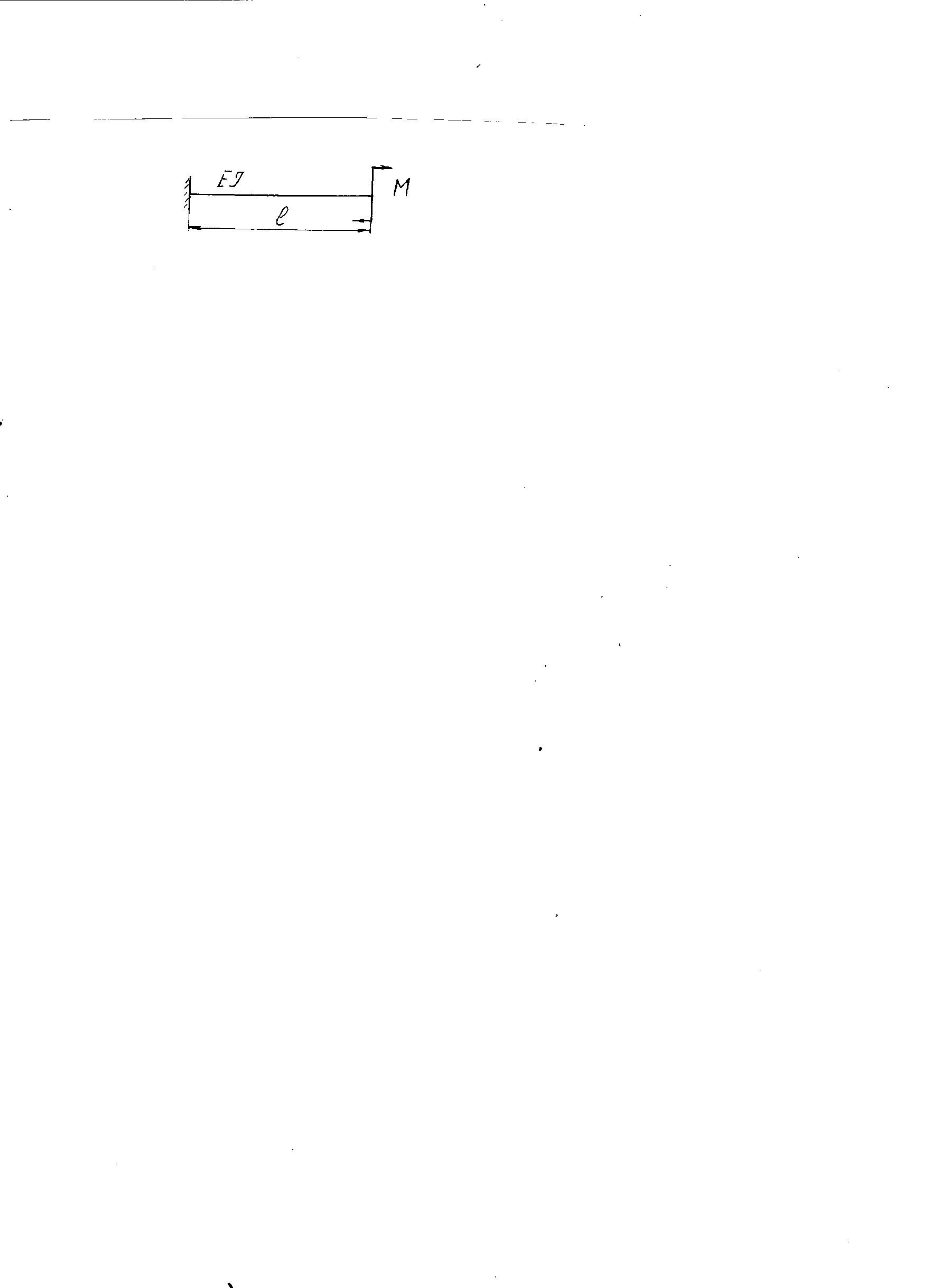 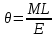 Определить угол поворота сечения балки над правой опорой  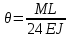 Определить прогиб концевого сечения балки 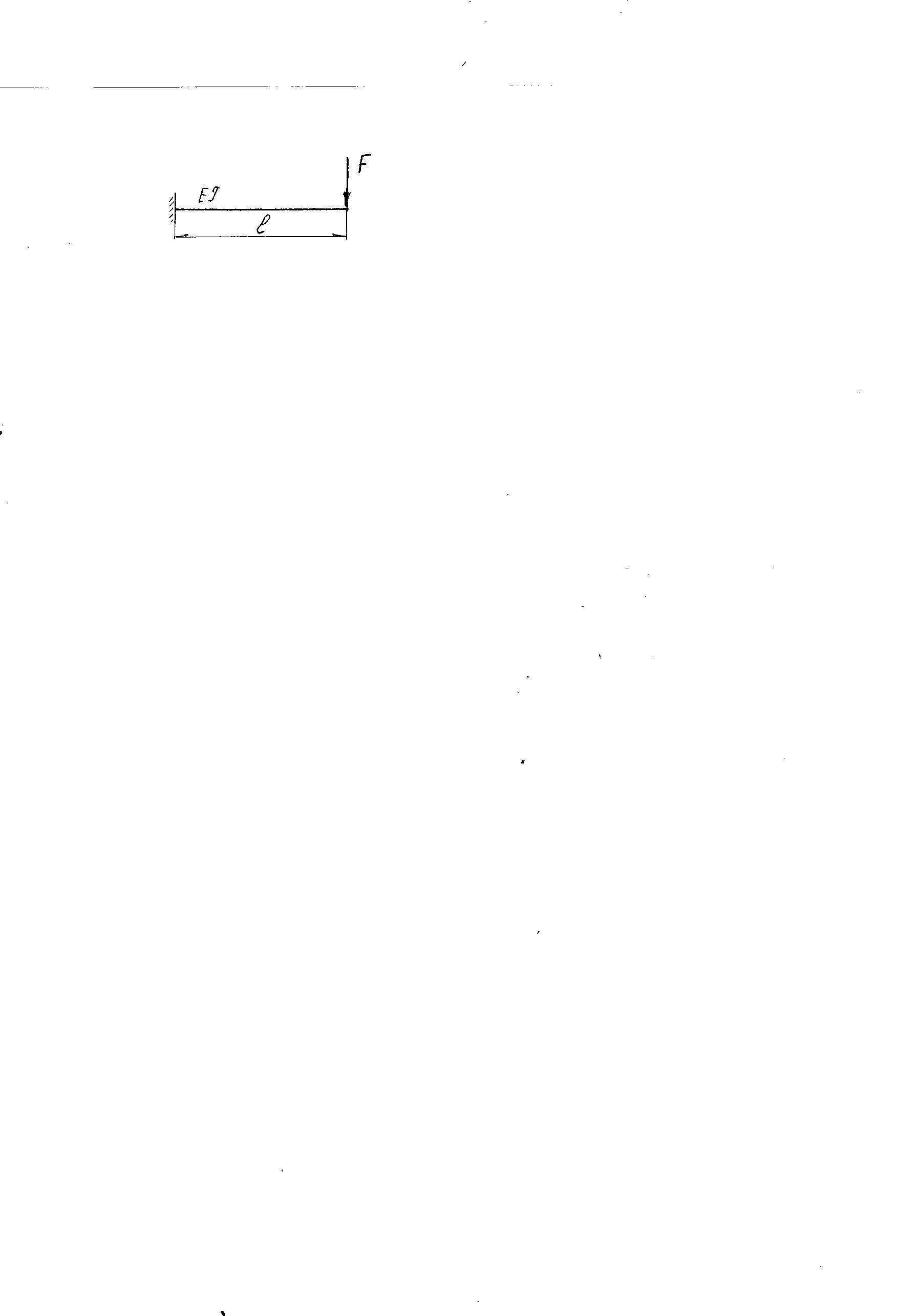 y= 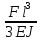 Определить угол поворота концевого сечения балки 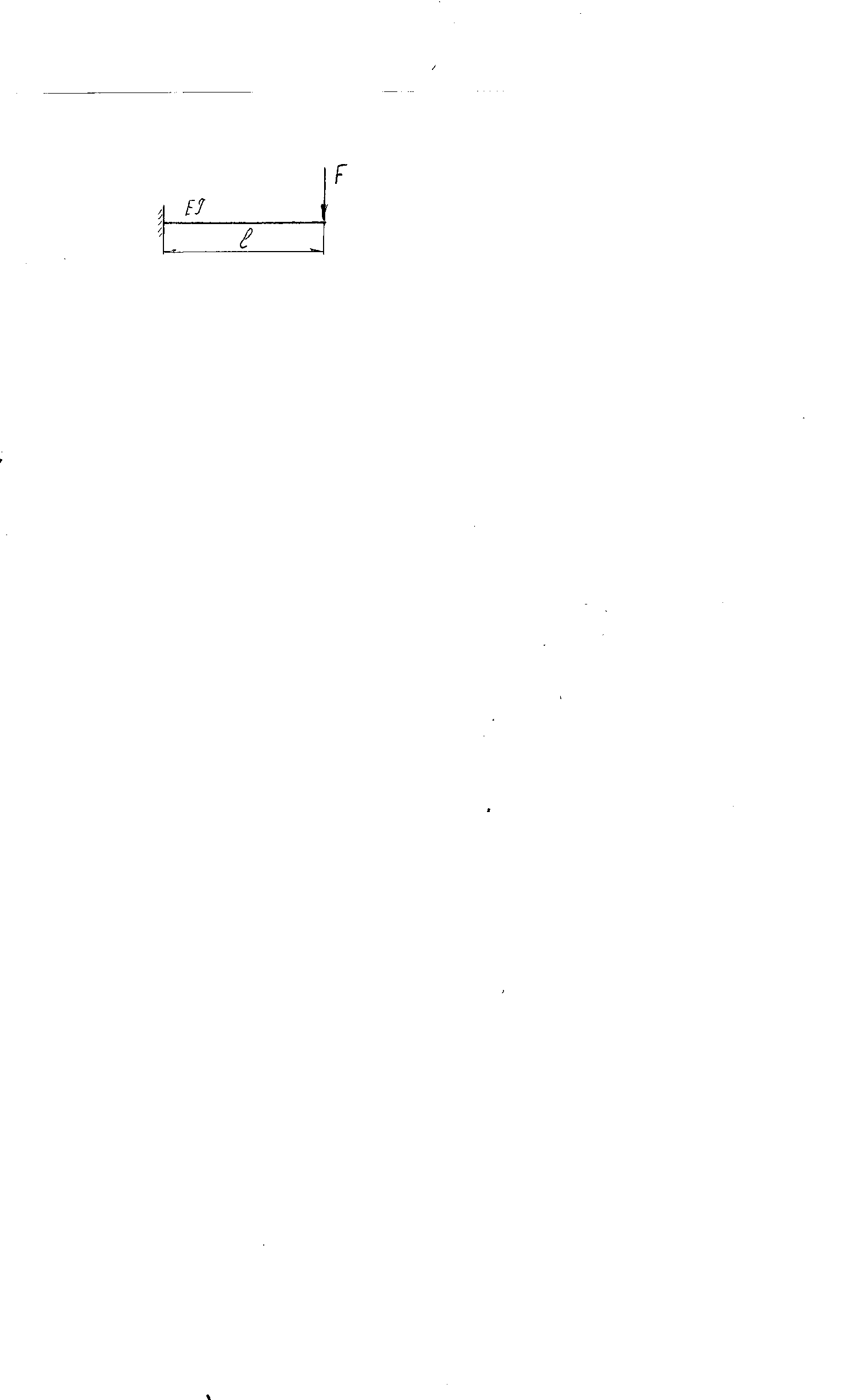 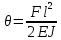  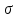 = =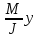 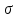 = =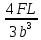 J= J=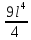 ??? Степень статической неопределённости для плоского замкнутого контура равна: Число лишних связей, удаление которых превращает статически неопределимую систему в статически определимую. Что такое момент сопротивления при изгибе и какова его размерность? Отношение момента инерции относительно данной осени к расстоянию от осени до наибольшей удалённой точки поперечного сечения W=Yv/Yмал [см*3]. По какой формуле определяются касательные напряжения при поперечном изгибе? По формуле Журавского, Q-попереч сила в сечении балки; ский момент; Jx-момент инерции; b- напряжение распределенное по ширине балки. (Формула). Для заданной статически неопределимой балки представлены четыре варианта основной системы метода сил. Неправильный ответ соответствует варианту: 2 Система канонических уравнений имеет вид: бik•Xk+/\iF=0. Произведение бik•Xk - это перемещение по направлению от силы Хк. В чем заключается проверка эпюр Q и M при изгибе? В проверке условий равновесия узла. На каком волокне поперечного сечения палки изображаются эпюра изгибающих моментов? На растянутом. Как расположены нейтральные слой и нейтральная ось при поперечном изгибе? Нейтральная ось проходит через центр тяжести сечения. А слой между которым сжимается и растягивается не изменяя длины. По какой формуле определяются нормальные напряжения в поперечным сечении балки при поперечном изгибе и как они изменяется по высоте балки? От действия изгибов момента в поперечных сечениях балки возникает нормальное напряжение(б=МУ1/J) M-изгибающий момент сечения; J-момент инерции поперечного сечения балки от нейтральной оси; У1- расстояние от нейтральной оси до точки. Что называется жёсткостью сечения при изгибе? Отклонение, кривизна изогнутой оси балки O-угол поворота; У- прогиб. | ||||||||||||||||||||