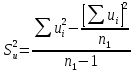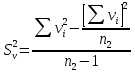реферат. МОРОЗ В Г. Современные проблемы системного анализа и управления курсовая работа аналитическая деятельность по сбору и обработке статистических данных о чрезвыча
 Скачать 232.49 Kb.
|
|
3. Проверка выдвинутой гипотезы по статистическим данным исследования I. Постановка задачи. ЦУКС ГУ МЧС России по Ленинградской области и ЕДДС районов Ленинградской области был проведен сбор данных о количестве происшествий возникающих на территории области поквартально за 2021 год Таблица 9. Таблица 9
Требуется: при условии, что результаты измерений распределены нормально и выборки независимы, проверить, обеспечивается ли одинаковая точность измерений этих двух групп при уровне значимости α=0,1 и α=0,05. Решение: О точности способов можно судить по величинам дисперсий. Примем за нулевую гипотезу равенство дисперсий: H0: D(X) = D(Y); тогда H1: D(X) ≠ D(Y). Для упрощения вычислений перейдем к условным вариантам (Таблица 10) для нахождения исправленных выборочных дисперсий: ui= 10xi – 1000; vi= 10yi – 1000; Таблица 10
Далее находим исправленные выборочные дисперсии по формулам (15):
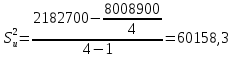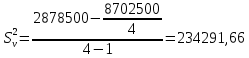  Следующим шагом проводится сравнение исправленных дисперсий и находится отношение большей дисперсии к меньшей. 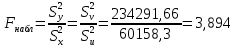 По условию конкурирующая гипотеза имеет вид H1: D(X) ≠ D(Y), поэтому критическая область двусторонняя, поэтому при отыскании критической точки следует брать уровень значимости α/2. По таблице распределения Фишера-Снедекора находим значение Fкрит. Числа степеней свободы: m1=n1-1=3 m2=n2-1=3 Для уровня значимости α=0,1 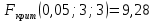 Для уровня значимости α=0,05 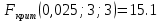 Как видно при сравнении обоих полученных результатов 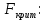 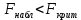 , в следствие чего гипотеза H0 о равенстве генеральных дисперсий принимается. 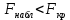при уровне значимости и α=0,05 и α=0,1, исходя из этого нет оснований отвергать гипотезу о равенстве генеральных дисперсий. Таким образом, выборочные исправленные дисперсии различаются незначительно, следовательно одинаковую точность измерений обеспечивают и ЦУКС, и ЕДДС муниципальных районов.Заключение В ходе выполнения работы проведено исследование конкретной генеральной совокупности, которая представляет собой результаты экспериментальных наблюдений по количеству происшествий и чрезвычайных происшествий на объектах промышленности на территории Ленинградской области. В результате выполнения данной курсовой работы были: - закреплены теоретические знания и практические навыки по математической статистике; - разработан плана статистического наблюдения на основе данных исследования - изучены и сформулированы выводы о законе распределения, наличии и характере статистической связи между исследуемыми признаками; - рассмотрен корреляционный и регрессионный анализ числовых признаков X и Y. - проведена проверка выдвинутой гипотезы по статистическим данным исследования. Список используемой литературы Системный анализ и принятие решений: учебник / под общей ред. В.С. Артамонова. СПб.: Изд-во СПб УГПС МЧС РФ, 2009. 378 с. Вентцель Е.С. Исследование операций. Задачи, принципы, методология: учеб. пособ. для студ. втузов. 4-е изд. стер. М.: Высш. шк., 2007. - 208 с. Гмурман В.Е. Теория вероятностей и математическая статистика: учеб. пособ. для вузов. 7-е изд., стер. М.: Высш. шк., 2004. 479 с. 4. Вентцель Е. С. Теория вероятностей: учеб. – 11-е изд., стер. – М.: КНОРУС, 2010. – 664 с. 5. Приказ МЧС России от 08.07.2004 № 329 «Об утверждении критериев информации о чрезвычайных ситуациях» (с изменениями и дополнениями) (зарегистрирован в Минюсте России 12.12.2008, регистрационный N 12842). 6. Системный анализ в управлении: учеб. пособ. / В.С. Анфилатов, А.А. Емельянов, А.А. Кукушкин. М.: Финансы и статистика, 2002. - 368 с. 7. Исследование операций: учеб. пособ. для вузов / А.А. Васин, П.С. Краснощеков, В.В. Морозов. М.: Академия, 2009. - 464 с. | |||||||||||||||||||||||||||||||||||||||||
