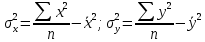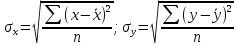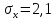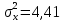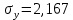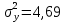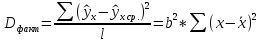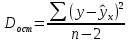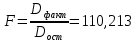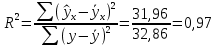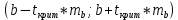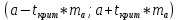реферат. МОРОЗ В Г. Современные проблемы системного анализа и управления курсовая работа аналитическая деятельность по сбору и обработке статистических данных о чрезвыча
 Скачать 232.49 Kb. Скачать 232.49 Kb.
|
|
2. Оценка уравнения регрессии по статистическим данным исследования I. Постановка задачи. Имеются: сведения о происшествиях и чрезвычайных ситуациях на объектах производства и количестве погибших за период с 2013 г. по 2019 г., отражённые в Таблице 5: Таблица 5.
Требуется: дать оценку уравнения регрессии по представленным статистическим данным. II. Составление уравнения регрессии и оценка его значимости. а) Построение уравнения регрессии. Для составления уравнения регрессии выполним необходимые расчеты и приведём их в Таблице 6: Таблица 6.
Исходя из данных, приведенных в таблице 6, найдем коэффициенты a и b формулы (2) и (3), и построим уравнение регрессии (1). 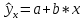 (1) (1)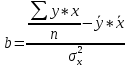 (2) (2)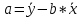 (3) (3)Среднее значение x и yопределим по формулам (4) и (5) при п=7: 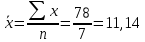 (4) (4)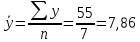 (5) (5)Рассчитаем значения дисперсии и СКО по формулам (6) и (7):
Тогда в соответствии с формулами (2) и (3) находим коэффициенты: 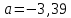 , , 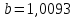 и уравнение регрессии будет иметь вид: и уравнение регрессии будет иметь вид: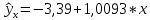 Коэффициент линейной парной регрессии может быть рассчитан через коэффициент уравнения регрессии b: 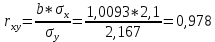 Получив значение коэффициента 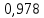 выяснили, что качественная характеристика силы связи весьма высокая. выяснили, что качественная характеристика силы связи весьма высокая.На Рисунке 1 представлено графическое представление уравнение регрессии. 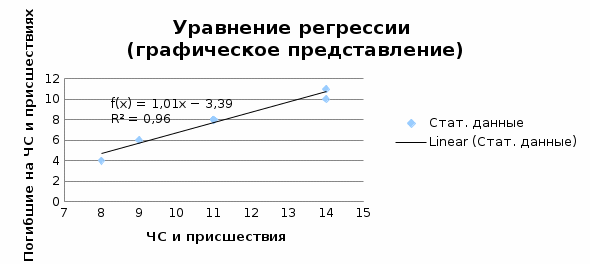 Рисунок 1 б) Проверим значимость построенного уравнения по F-критерию, вычислив коэффициент детерминации. В качестве основной (нулевой) гипотезы выдвигают гипотезу о незначимом отличии от нуля параметра или статистической характеристики в генеральной совокупности. Наряду с основной (проверяемой) гипотезой выдвигают альтернативную (конкурирующую) гипотезу о неравенстве нулю параметра или статистической характеристики в генеральной совокупности. Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равны нулю) на уровне значимости 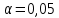 . .H0: 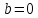 , то есть между переменными x и y отсутствует линейная взаимосвязь в генеральной совокупности; , то есть между переменными x и y отсутствует линейная взаимосвязь в генеральной совокупности;H1: 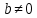 , то есть между переменными x и y есть линейная взаимосвязь в генеральной совокупности. , то есть между переменными x и y есть линейная взаимосвязь в генеральной совокупности.Значимость уравнения регрессии проверяется на основе F – теста, который заключается в проверке гипотезы Н0 о статистической не значимости показателя тесноты связи. Для этого определяется факторная Dфакт (8) и остаточнаяDост(9) дисперсии, рассчитанные на одну степень свободы вариации. Расчет производится по следующим формулам:
1 – число степеней свободы.
(n–2)– число степеней свободы вариации или число свободно варьирующих элементов совокупности. Получаем: общая сумма квадратов отклонений: S(y-y̅ )2 = 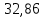 факторная сумма квадратов: 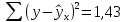 остаточная сумма квадратов: 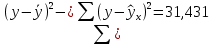 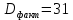 ,96 ,96 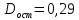 Как видно из полученных результатов, разница между факторной дисперсией и остаточной значительна, следовательно, фактор оказывает существенное влияние на Х. Расчетную величину F–критерия Фишера получим, сопоставив факторную и остаточную дисперсии (10):
Если вычисленное значение F-критерия Фишера оказывается больше табличного значения F, то нулевая гипотеза Н0 об отсутствии связи между признаками отклоняется и делается вывод о существенности связи между признаками. Если же расчетная величина F–критерия окажется меньше Fтабл., уравнение регрессии считается статистически незначимым. Для проверки расчетного значения F-критерия, воспользуемся Таблицей 7, при 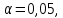 где: где:m1 - число степеней свободы факторной дисперсии (m1 =1); m2 – число степеней свободы остаточной дисперсии, (m2 =5). Таблица 7.
Поскольку Fтабл. < Fфакт. (6,61 < 110,213) при 5% уровне значимости, то можно сделать вывод о значимости уравнения регрессии. Рассчитаем коэффициент детерминации для оценки качества подбора уравнения регрессии (11):
Из полученного результата видно, что уравнение регрессии объясняет 98% дисперсии результативного признака, т.е. в 97% случаев изменения х приводят к изменению y, а на долю случайных факторов приходится 3% от ее значения. Оценка значимости уравнения регрессии приведена в Таблице 8. Таблица 8
в) Оценка статистической значимости коэффициентов регрессии и корреляции по t-критерию Стьюдента путем сопоставления их значений с величиной случайной ошибки, рассчитанной для каждого параметра. Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитывается t-критерий Стьюдента и доверительные интервалы каждого из показателей. Выдвинем гипотезу H0 о случайной природе показателей, т.е. незначительном их отклонении от нуля. В случае если основная гипотеза окажется неверной, мы принимаем альтернативную. H0: 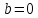 , то есть линейной взаимосвязи между переменными x и y в генеральной совокупности нет; , то есть линейной взаимосвязи между переменными x и y в генеральной совокупности нет;H1: 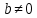 , есть линейная взаимосвязь между переменными. , есть линейная взаимосвязь между переменными.Найденное по данным наблюдениям значение t-критерия сравнивается с табличным (критическим) значением, определенным по таблице распределения Стьюдента. Табличное значение определяется в зависимости от уровня значимости 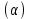 и числа степеней свободы, которое в случае линейной парной регрессии равно (n-2), n – число наблюдений. и числа степеней свободы, которое в случае линейной парной регрессии равно (n-2), n – число наблюдений.Если |tнабл| > tкрит, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза Н0, утверждающая равенство нулю коэффициента корреляции, отвергается). Если |tнабл| < tкрит, то нет оснований отвергать основную гипотезу, т.е. параметр или статистическая характеристика в генеральной совокупности незначимо отличается от нуля при уровне значимости 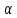 . .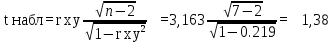 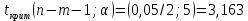 где m=1 – количество объясняющих переменных. Поскольку 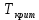 > > 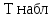 , то принимаем гипотезу о равенстве 0 коэффициента ранговой корреляции Спирмена. Другими словами, коэффициент ранговой корреляции статистически - не значим и ранговая корреляционная связь между оценками по двум тестам незначимая. , то принимаем гипотезу о равенстве 0 коэффициента ранговой корреляции Спирмена. Другими словами, коэффициент ранговой корреляции статистически - не значим и ранговая корреляционная связь между оценками по двум тестам незначимая. Проверим гипотезу H0: гетероскедастичность отсутствует. Поскольку 3.163 > 1.38, то гипотеза об отсутствии гетероскедастичности принимается. Оценка значимости коэффициентов регрессии и корреляции с помощью t–критерия Стьюдента проводится ещё и путем сопоставления их значений с величиной случайной ошибки, рассчитываемой для каждого параметра (12): 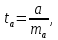 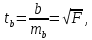 (12) (12)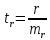 Случайные ошибки параметров линейной регрессии a (13) и b(14), а также коэффициента корреляции r (15) определяются по формулам: 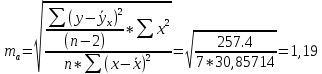 (13) (13)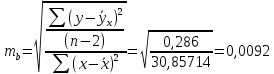 (14) (14)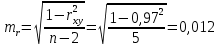 (15) (15)Связь между F–критерием Фишера и t–критерием Стьюдента можно выразить равенством tr= tb= 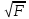 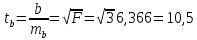 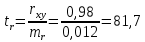 Поскольку 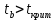 (10,5 > (10,5 > 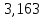 ), как и ), как и 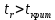 (81,7 > (81,7 > 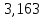 ) при 5% уровне значимости, то статистическая значимость коэффициента регрессии b и коэффициента корреляции r подтверждается (отвергаем гипотезу о равенстве нулю этих коэффициентов). ) при 5% уровне значимости, то статистическая значимость коэффициента регрессии b и коэффициента корреляции r подтверждается (отвергаем гипотезу о равенстве нулю этих коэффициентов).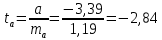 Поскольку 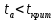 (-2,84 < (-2,84 < 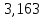 ) при 5% уровне значимости можно отбросить гипотезу о существенности коэффициента регрессии a, (принимаем гипотезу о равенстве нулю этого коэффициента), что означает возможность пренебречь в данном случае коэффициентом a. ) при 5% уровне значимости можно отбросить гипотезу о существенности коэффициента регрессии a, (принимаем гипотезу о равенстве нулю этого коэффициента), что означает возможность пренебречь в данном случае коэффициентом a.г) Оценка доверительных интервалов коэффициентов регрессии. Определим доверительные интервалы коэффициентов регрессии (16):
Значение доверительного интервала для коэффициента регрессии b: 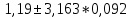 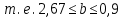 Значение доверительного интервала для коэффициента регрессии 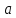 : :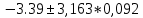 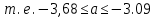 С вероятностью 95% можно утверждать, что значения данных параметров будут лежать в найденном интервале. Проведеная проверка статистической значимости коэффициента регрессии, которая показала, что коэффициент b- статистически значим, в то время как значимость коэффициента регрессии a несущественна. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||