№12 класс 6Г. Создание конуса, целиндра и сферы
 Скачать 463.52 Kb. Скачать 463.52 Kb.
|
Ход урока:
Конспект урока математики 6 класс Тема урока: «ШАР. КОНУС.ЦИЛИНДР» Содержание Шар. Конус. Цилиндр. Многогранники. Тела вращения. Цель урока Познакомить учащихся с геометрическими телами – шаром, конусом, цилиндром и их элементами. Научить различать в окружающем мире предметы, имеющие форму изучаемых фигур. Планируемые результаты Уметь оперировать понятиями: шар, конус, цилиндр, многогранник, тело вращения, поверхность тела, сечение. Уметь распознавать изученные геометрические фигуры. Уметь приводить примеры предметов, имеющих форму изученных тел вращения. Уметь рассказывать о шаре, конусе, цилиндре по плану. Оборудование Чертежные инструменты. Ребусы. Рисунки к устным задачам. Ход урока …На сегодняшнем уроке вы познакомитесь с тремя новыми геометрическими фигурами. Чтобы лучше понять изучаемый материал будьте внимательными, активными и сообразительными. Тема урока состоит из трёх слов, которые зашифрованы с помощью ребусов. Разгадайте их, и вы узнаете какие геометрические фигуры мы будем изучать сегодня.
(Шар) (Конус) (Цилиндр) Приступим к изучению новых фигур, которые будем изучать по плану, записанному на доске. План Происхождение названия фигуры. Примеры. Поверхность. Сечения. Начнём с цилиндра. Оказывается, слово «цилиндр» произошло от греческого слова «кюлиндрос», означающего «валик», «каток». На рубеже XVIII - XIX веков мужчины многих стран носили твёрдые шляпы с небольшими полями, которые так и назывались цилиндрами из-за большого сходства с геометрической фигурой цилиндром. Какие ещё предметы имеют цилиндрическую форму? (Стакан, карандаш, многие баночки, кастрюли, бидоны, часть скалки…).  Внимательно посмотрите на цилиндр (демонстрируется модель). Цилиндр, как мы видим, пространственная или объёмная фигура. Поверхность цилиндра состоит из двух оснований и боковой поверхности. Что из себя представляют основания цилиндра? (Круги) Что вы можете сказать о размерах этих кругов? (Одинаковые, т.е. радиусы этих кругов равны) Что из себя представляет боковая поверхность? (Затрудняются ответить) Возьмём бумажный цилиндр, разрежем его следующим образом (показываю) и развернём. Так что же представляет собой боковая поверхность? (Прямоугольник) Что ещё нужно знать о цилиндре? Высота цилиндра – это расстояние между основаниями, радиус цилиндра – радиус круга, являющегося основанием цилиндра. Ц и л и н д р
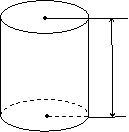 радиус радиусА сейчас представьте, что у каждого из вас в руках деревянный цилиндр и топорик, с помощью которого вы легко можете рассечь или расколоть цилиндр. «Аккуратно» топориком ударяем по верхнему основанию и раскалываем его (показываю на модели). Он распадётся на две половинки. Форму какой геометрической фигуры имеет срез или по научному говорят сечение цилиндра? Многие, наверно, видели как колют дрова! (Прямоугольник) А сейчас будем «пилить» цилиндр, положив его «на бок». Мысленно его распилим или рассечём. Какая геометрическая фигура получится на срезе или говорят в сечении цилиндра? (Круг) Продолжаем трудиться дальше, опять положим цилиндр на боковую поверхность, но рассечём его уже «наискосок». Какая геометрическая фигура будет в сечении, т.е. на срезе? (Овал) Овал, по-научному, эллипс (заранее записать на центральной доске под цилиндром). Итак, какие геометрические фигуры могут быть в сечении цилиндра? (Прямоугольник, круг, эллипс) Все пункты плана разобраны, вы уже достаточно много знаете о цилиндре. Переходим к рассмотрению конуса. Слово «конус» произошло от греческого слова «конос», означающего сосновую шишку (показываю шишку). Действительно, есть некоторое сходство. Конус, как и цилиндр, является пространственной фигурой. Поверхность конуса состоит из круга, который называется основанием конуса и боковой поверхности. Что же из себя представляет боковая поверхность? (Затрудняются ответить) Трудно мысленно представить боковую поверхность конуса, поэтому, как и в случае с цилиндром, возьмём бумажный конус, разрежем его следующим образом (показываю) и развернём. Что является развёрткой боковой поверхности конуса? Что это такое? Частью какой геометрической фигуры является эта фигура? (Часть круга) Конус, в отличие от цилиндра, имеет вершину (показываю вершину, высоту и радиус основания по рисунку на центральной доске). К о н у с
 радиус радиус Если вершину и верхнюю часть конуса отсечь (показываю на модели), то мы получим так называемый усечённый конус. Подумайте и скажите, какие предметы имеют форму конуса или усечённого конуса? (Ведро, горшки для цветов, воронка, мороженое-рожок…) А сейчас снова представим, что мы рассекаем деревянный конус. 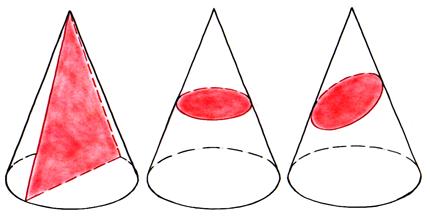 Формы каких геометрических фигур могут иметь сечения конуса? ( Треугольника, круга, эллипса ) Оказывается, сечения конуса могут иметь формы других геометрических фигур, названия которых мы даже ещё не знаем, их будем изучать в старших классах, и поэтому о них пока говорить не будем. Снова все пункты плана нами рассмотрены. И, наконец, переходим к изучению шара. Шар – это наиболее знакомая вам геометрическая фигура. Мяч (показываю) – пример предмета шарообразной формы. Какие ещё предметы имеют форму шара? Ребята, кому я сейчас брошу этот мяч, нужно привести свой пример предмета, имеющего форму шара. Расскажите, что вы знаете о шаре? Сообщение «ШАР» Шар – это пространственная фигура. Поверхность шара называют сферой. Слово «сфера» произошло от греческого слова «сфайра», которое переводится на русский язык как «мяч». Не нужно путать понятия «шар» и «сфера». Сфера – это, можно сказать, оболочка или граница шара. Мяч, глобус – это сферы, а вот арбуз, апельсин, Солнце, Луна, Земля и остальные планеты имеют форму немного сплющенного шара (показывает рисунок).  Сфера обладает очень интересным свойством – все её точки одинаково удалены от центра шара. 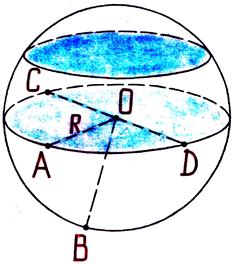 Отрезок, соединяющий любую точку сферы с центром шара, называется радиусом шара. На рисунке отрезки ОА, ОВ, О D и ОС являются радиусами (показывает по рисунку). Отрезок, соединяющий две точки сферы и проходящий через центр шара, называется диаметром шара. На рисунке отрезок С D является диаметром шара. Диаметр шара равен двум радиусам. Любое сечение шара имеет вид круга. Если рассекать шар ближе к центру, то круги будут больше, если дальше от центра, то радиусы кругов будут меньше. Итак, мы познакомились с тремя пространственными геометрическими фигурами – шаром, цилиндром и конусом. Вы должны знать, что пространственные геометрические фигуры ещё по-другому называют геометрическими телами. Оказывается, все геометрические тела математики раздели на две группы: так называемые многогранники и так называемые тела вращения. Внимательно посмотрите на геометрические тела (показываю модели) и попробуйте догадаться, какое геометрическое тело относится к какой группе. Как называется фигура, и к какой группе её отнесём? Действительно, шар, цилиндр, конус, усечённый конус – тела вращения. А куб, параллелепипед, пирамида – многогранники. Почему куб, параллелепипед, пирамиду вы отнесли к многогранникам? (Много граней) Логично! А вот почему шар, цилиндр, конус, усечённый конус назвали телами вращения, об этом я вам расскажу сама. Дело тут вот в чём! Если взять плоскую фигуру круг или даже достаточно половину круга (полукруг) и вращать его вокруг диаметра, то в воздухе он опишет шар. Значит, шар получился в результате вращения полукруга. Вот почему шар является телом вращения, а прямая, вокруг которой производили вращение, называется осью вращения шара или просто осью шара. Попробуйте догадаться: Какая плоская фигура при вращении опишет цилиндр? (Прямоугольник) Какая прямая будет его осью? (Осью является неподвижная сторона прямоугольника) Какая плоская фигура при вращении опишет конус? (Прямоугольный треугольник) Какая прямая будет его осью? (Ось – неподвижная сторона) В дальнейшем на уроках математики будем более подробно изучать эти тела, и вы узнаете о существовании других многогранников, а также узнаете формулы, по которым находятся объёмы этих пространственных фигур. Решим несколько задач. 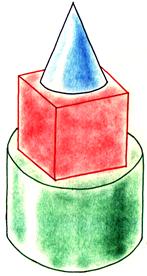 Задача № 1. Из предметов какой формы сложена башня? Называйте сверху вниз. (Конус, куб, цилиндр) Задача № 2. На рисунке изображены различные геометрические тела. Какие из них являются многогранниками? 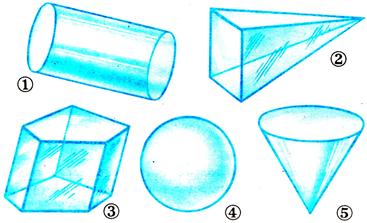 Второе (пирамида), третье (наклонная призма) Задача № 3. На рисунке в первой строчке изображён вид фигуры спереди, а во второй строчке – вид фигуры сверху. Какая это фигура? 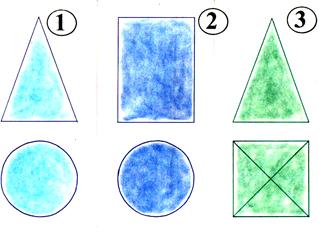  1.Конус. 2.Цилиндр. 3.Четырёхугольная пирамида. 4.Прямоугольный параллелепипед. 5.Треугольная пирамида. 6.Шар. Если на конус посмотреть сверху, то мы увидим круг, а если сбоку, то – треугольник. Зная это, решим следующую задачу.  Задача № 4. На круглом столе стоят три конуса разного цвета – красный, синий и зелёный. Вокруг стола сидят дети: Маша, Ваня, Даша, Коля, Рая и Петя. Кто из детей видит такую картину, как изображено на рисунке под буквой а); б); в)? а) б) в) 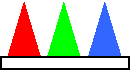 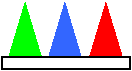 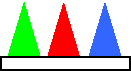 (Петя) (Ваня) (Маша) Задача № 5. На рисунке изображены некоторые геометрические тела. Возможно, точка зрения не очень привычна. Какие тела, если на них смотреть с соответствующей стороны, могут выглядеть, как на рисунке? Какие из рисунков могут соответствовать одному и тому же телу? 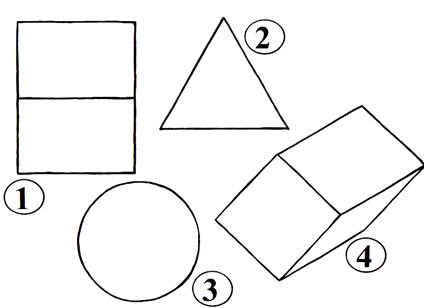 1. Куб или параллелепипед. 2. Пирамида или конус. 3. Конус, цилиндр или шар. 4. Параллелепипед . 2 и 3 рисунки могут соответствовать конусу, а 1 и 4 – параллелепипеду. Итак, все задачи решены… А сейчас скажите: Чем мы сегодня занимались на уроке? (Изучали тела вращения: конус, шар, цилиндр) На какие две группы делятся все геометрические тела? (Многогранники, тела вращения) При вращении какой плоской фигуры образуется цилиндр? (Прямоугольника) Приведите примеры тел конической формы. (Воронка, ведро, горшок для цветов, мороженое- рожок …) Какие фигуры могут быть в сечении конуса? (Треугольник, круг, эллипс)? Чем отличаются понятия «шар» и «сфера»? (Сфера – это только поверхность шара, а шар – часть пространства, ограниченное сферой) Домашнее задание: рассказ по плану I ряду – о цилиндре, II ряду – о конусе, III ряду – о шаре; на альбомном листе нарисовать предметы, имеющие форму вновь изученных геометрических фигур. Приложение Стенд «Сегодня на уроке»  На рисунке 1, а изображен цилиндр. Сверху и снизу цилиндр ограничен кругами, которые называются основаниями цилиндра. Развертка боковой поверхности цилиндра – прямоугольник. На рисунке 1, б изображена развертка поверхности цилиндра. Попробуйте вычислить площадь поверхности цилиндра, если его высота 5 см , а радиус оснований 2 см . Ц и л и н д р 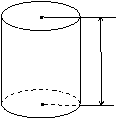 а) радиус б)высота Рис. 1.  На рисунке 2, а изображен конус. Основание конуса – круг, а развертка боковой поверхности – сектор (см. рис. 2, б). Вычислите площадь поверхности конуса, если радиус его основания 3 см , а развертка боковой поверхности – сектор с прямым углом, радиус этого сектора 12 см . Есть ли в условии задачи лишние данные? К о н у с  а) высота; б) радиус Литература Математика: 6 класс: учебник для учащихся общеобразовательных учреждений / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2013. Сборник задач и заданий для тематического оценивания по математике для 6 класса / А.Г. Мерзляк, В.Б. Полонский, Рабинович Е.М., М.С. Якир. — Харьков: Гимназия, 2010. Математика: 6 класс: рабочая тетрадь / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. — М.: Вентана-Граф, 2013. ________________________________________ ВЫСКАЗЫВАНИЯ О МАТЕМАТИКЕ Данные высказывания можно использовать для оформления зала, кабинета математики. • Математика - это язык, на котором написана книга природы . (Г. Галилей) • Математика – царица наук, арифметика – царица математики . (К.Ф. Гаусс) • Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает на¬стойчивость и упорство в достижении цели. (А. Маркушевич) • «Числа управляют миром», – говорили пифагорейцы. Но числа дают возможность человеку управлять миром, и в этом нас убеждает весь ход развития науки и техники наших дней. (А. Дородницын) • Рано или поздно всякая правильная математическая идея находит применение в том или ином деле. (А.Н. Крылов) • Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой, пока есть к тому возможность. Она окажет вам потом огромную помощь во всей вашей работе. (М.И. Калинин) • Разве ты не заметил, что способный к математике изощрен во всех науках в природе? (Платон) • Было бы хорошо, если бы эти знания требовало само госу¬дарство и если бы лиц, занимающих высшие государственные должности, приучали заниматься математикой и в нужных случаях к ней обращаться. (Платон) • Науки математические с самой глубокой древности обращали на себя особенное внимание, в настоящее время они полу¬чили еще больше интереса по влиянию своему на искусство и промышленность. (П.Л. Чебышев) • Математика есть лучшее и даже единственное введение в изу¬чение природы. (Д.И. Писарев) • Астрономия (как наука) стала существовать с тех пор, как она соединилась с математикой. (А.И. Герцен) • Полет – это математика. (В. Чкалов) • Вдохновение нужно в геометрии не меньше, чем в поэзии. (А.С. Пушкин) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||