Сплайн. Сплайнфункции
 Скачать 90.41 Kb.
|
|
Сплайн-функции Пусть на отрезке  задано разбиение , в узлах которого известны значения достаточно гладкой функции  :  ,  . Узлы разбиения делят отрезок на  отрезков  ,  ,...,  .Сплайном называется составная функция  , которая вместе с производными нескольких порядков непрерывна на всем отрезке , а на каждом частичном отрезке  в отдельности является составляющей функцией  Рассмотрим частный случай, когда функции  являются алгебраическими многочленами вида  где  — коэффициенты, определяемые для каждого частичного отрезка.Максимальная по всем частичным отрезкам степень многочлена называется степенью сплайна, а разность между степенью сплайна и порядком наивысшей непрерывной на производной — дефектом сплайна.Линейный сплайн Сплайн состоит из линейных многочленов вида
Параметры сплайна  ,  ,  , определим из условия непрерывности на и требования совпадения значений сплайна с функцией в узловых точках
Обозначим  . Тогда для каждого из многочленов можно записать   и для определения коэффициентов линейного сплайна (7.10) получим уравнения   Пример Для значений  ,  ,  ,  построим линейный сплайн. Коэффициенты сплайна имеют следующие значения 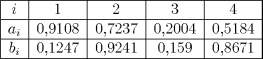 На рис. 7.2 в виде точек приведены заданные значения, линейный сплайн (ломаная линия), а также для сравнения график функции  , значения которой являются исходными данными для построения сплайна.
Параболический сплайн Сплайн 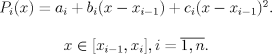состоит из парабол, то есть многочлен  имеет вид  Для определения коэффициентов сплайна дополнительно к условиям (7.11), (7.12) потребуем непрерывности первой производной сплайна на интервале , то есть
Обозначив ,  , и, учитывая, что  в соответствии с формулами (7.11), (7.12) и (7.13) получим
Тогда коэффициенты , , определяются согласно (7.14), а (7.15) можно записать в виде
Если теперь запишем выражения для и  в виде (7.17) и подставим их в (7.16), то получим
где  Таким образом, уравнения (7.14), (7.17) и (7.18) образуют систему из  уравнений для определения  коэффициентов сплайна. Недостающее уравнение получается из дополнительного условия, которое накладывается на значение производной сплайна на конце интервала , в виде 
Если подставить в (7.19) выражение для  из (7.17), то формулу (7.19) можно переписать в виде  где  Тогда
Таким образом, параметры параболического сплайна вычисляются в следующем порядке: сначала в обратном порядке вычисляются коэффициенты  ,  , по (7.20), (7.21), затем , , по (7.16)или (7.17), а затем , , по (7.14).Пример Для значений , ,  , построим параболический сплайн. Коэффициенты сплайна имеют следующие значения: 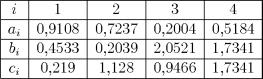 На рис. 7.3 приведены в виде точек заданные значения, параболический сплайн, а также, для сравнения, график функции , значения которой являются исходными данными для построения сплайна.
|
