Мат моделирование. Способ подстановки Метод преобразования таблицы с разрешающим элементом
 Скачать 44.79 Kb. Скачать 44.79 Kb.
|
|
Задание 1 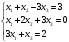 Способ подстановки 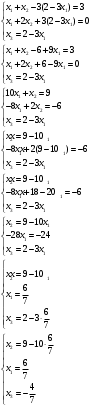 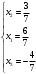 Метод преобразования таблицы с разрешающим элементом
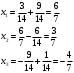 Метод ноль таблиц
Метод Гаусса Запишем систему в виде расширенной матрицы: Умножим 2-ю строку на (-1). Добавим 2-ю строку к 1-й: Умножим 2-ю строку на (3). Умножим 3-ю строку на (-1). Добавим 3-ю строку к 2-й: Умножим 1-ю строку на (6). Добавим 2-ю строку к 1-й: Теперь исходную систему можно записать так: x3 = 16/(-28) x2 = [-2 - (8x3)]/6 x1 = [2 - (x3)]/3 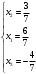 Задание 2 Чтобы обеспечить сбалансированное питание для собак в питомнике, корм готовится из смеси трех зерновых круп. Соответствующие данные приведены в таблице.
Каждая собака должна употребляла ежедневно не менее 580 г. белков, 170 г. углеводов и не более 80 г. жиров. Сколько каждой крупы должна получать собака, чтобы минимизировать затраты? Пусть х1, х2, х3 количество круп В, С, D. Составим математическую модель задачи 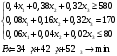 Расширенная матрица системы ограничений-равенств данной задачи: Приведем систему к единичной матрице методом жордановских преобразований. 1. В качестве базовой переменной можно выбрать x4. Получаем новую матрицу:
2. В качестве базовой переменной можно выбрать x5. 3. В качестве базовой переменной можно выбрать x3. Разрешающий элемент РЭ=0.32. Строка, соответствующая переменной x2, получена в результате деления всех элементов строки x3 на разрешающий элемент РЭ=0.32. На месте разрешающего элемента получаем 1. В остальных клетках столбца x2 записываем нули. Все остальные элементы определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы:
Получаем новую матрицу:
Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (4,3,5). Соответствующие уравнения имеют вид: -0.32x1-0.22x2+x4 = -410 1/4x1+0.5x2+x3 = 531.25 11/200x1+0.03x2+x5 = 69.375 Выразим базисные переменные через остальные: x4 = 0.32x1+0.22x2-410 x3 = -1/4x1-0.5x2+531.25 x5 = -11/200x1-0.03x2+69.375 Подставим их в целевую функцию: F(X) = 34x1+42x2+52(-1/4x1-0.5x2+531.25) или F(X) = 21x1+16x2+27625 → min Система неравенств: 0.32x1+0.22x2-410 ≥ 0 -1/4x1-0.5x2+531.25 ≥ 0 -11/200x1-0.03x2+69.375 ≥ 0 Приводим систему неравенств к следующему виду: -0.32x1-0.22x2 ≤ -410 1/4x1+0.5x2 ≤ 531.25 11/200x1+0.03x2 ≤ 69.375 F(X) = 21x1+16x2+27625 → min Упростим систему. -0.32x1-0.22x2 ≤ -410 x1+2x2 ≤ 2125 11x1+6x2 ≤ 13875 F(X) = 21x1+16x2+27625 → min Если задача ЛП решается на поиск max-го значения, то стандартная форма будет иметь следующий вид: 0.32x1+0.22x2 ≤ 410 -x1-2x2 ≤ -2125 -11x1-6x2 ≤ -13875 F(X) = -21x1-16x2-27625 → max Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы. Поскольку в правой части присутствуют отрицательные значения, умножим соответствующие строки на (-1). Определим минимальное значение целевой функции F(X) = 21x1+16x2+27625 при следующих условиях-ограничений. При вычислениях значение Fc = 27625 временно не учитываем. 0.32x1+0.22x2-x4-410=410 1/4x1+0.5x2+x3+531.25=531.25 11/200x1+0.03x2+x5+69.375=69.375 Расширенная матрица системы ограничений-равенств данной задачи: Приведем систему к единичной матрице методом жордановских преобразований. 1. В качестве базовой переменной можно выбрать x4. Получаем новую матрицу:
2. В качестве базовой переменной можно выбрать x3. 3. В качестве базовой переменной можно выбрать x5. Поскольку в системе имеется единичная матрица, то в качестве базисных переменных принимаем X = (4,3,5). Выразим базисные переменные через остальные: x4 = 0.32x1+0.22x2-410 x3 = -1/4x1-0.5x2+531.25 x5 = -11/200x1-0.03x2+69.375 Подставим их в целевую функцию: F(X) = 21x1+16x2 Среди свободных членов bi имеются отрицательные значения, следовательно, полученный базисный план не является опорным. Вместо переменной x4 следует ввести переменную x2. Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
Представим расчет каждого элемента в виде таблицы:
Среди свободных членов bi имеются отрицательные значения, следовательно, полученный базисный план не является опорным. Вместо переменной x3 следует ввести переменную x1. Выполняем преобразования симплексной таблицы методом Жордано-Гаусса.
Представим расчет каждого элемента в виде таблицы:
Выразим базисные переменные через остальные: x2 = -3.05x3-2.38x4+642.857 x1 = 2.1x3+4.76x4+839.286 x5 = -0.024x3-0.19x4+3.929 Подставим их в целевую функцию: F(X) = 21(2.1x3+4.76x4+839.286)+16(-3.05x3-2.38x4+642.857)+27625 или F(X) = -4.76x3+61.9x4+55535.714 x2+3.05x3+2.38x4=642.857 x1-2.1x3-4.76x4=839.286 0.024x3+0.19x4+x5=3.929 При вычислениях значение Fc = 55535.714 временно не учитываем. Решим систему уравнений относительно базисных переменных: x2, x1, x5 Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (839.286,642.857,0,0,3.929)
Переходим к основному алгоритму симплекс-метода. Итерация №0. Текущий опорный план неоптимален, так как в индексной строке находятся положительные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x3, так как это наибольший коэффициент. Вычислим значения Di по строкам как частное от деления: bi / ai3 и из них выберем наименьшее: min (642.857 : 3.048 , - , 3.929 : 0.0238 ) = 165 Следовательно, 3-ая строка является ведущей. Разрешающий элемент равен (0.0238) и находится на пересечении ведущего столбца и ведущей строки.
Формируем следующую часть симплексной таблицы. Вместо переменной x5 в план 1 войдет переменная x3. Получаем новую симплекс-таблицу:
Конец итераций: индексная строка не содержит положительных элементов - найден оптимальный план Среди значений индексной строки нет положительных. Поэтому эта таблица определяет оптимальный план задачи. Окончательный вариант симплекс-таблицы:
Оптимальный план можно записать так: x1 = 1185, x2 = 140, x3 = 165, x4 = 0, x5 = 0 F(X) = 21*1185 + 16*140 + 52*165 = 54750 Так как масса была указана в граммах, то ответ нужно разделить на 1000 Ответ: x1=1,185кг; x2=0,14 кг; x3=0,165 кг; minF=55руб | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
