вопросы к экзамену. Вопросы к экзамену. Способы определения сторон горизонта
 Скачать 3.11 Mb.
|
12.Чтение топографических карт.13.Целеуказания по карте (по улитке).Целеуказание по карте включает определение по карте и передачу по техническим средствам связи или каким-либо другим способам данных о местоположении целей (объектов) на местности. В зависимости от обстановки и характера решаемых задач местоположение целей (объектов), нанесенных на карту, указывают различными способами: по квадратам координатной (километровой) сетки, прямоугольными, географическими координатами, от ориентира и полярными координатами. По квадратам координатной сетки указывают приближенное местоположение цели (объекта), когда достаточно знать, в каком квадрате координатной сетки карты цель находится (рис. 78). В письменном документе (донесении) квадрат указывают в скобках после наименования объекта. Мaтeриaл cooбщeствa «Tипичный Paзвeдчик». При устном докладе вначале называют квадрат, а затем наименование объекта, например : квадрат 5017, мост. Положение цели в квадрате может уточняться двумя способами (см. рис. 78): ✘ «по улитке» - квадрат делят на девять частей, которые обозначают цифрами; цифру, уточняющую местоположение объекта внутри квадрата, добавляют при целеуказании к обозначению квадрата, например КНП (5015 и 7); Для более точного указания местоположения объекта квадрат координатной сетки делят на девять частей, которые обозначают цифрами. Цифру, уточняющую местоположение объекта внутри квадрата, добавляют при целеуказании к обозначению квадрата, например, КНП (4914-9). Такое целеуказание называют целеуказанием «по улитке» . Его точность для карты масштаба 1 : 50 000 составляет около 300 м, а для карты масштаба 1 : 100000 — около 500 м. В отдельных случаях при уточнении местоположения объекта квадрат на карте делят на четыре части, обозначаемые прописными буквами, например, миномет (5013-А) . ✘по буквам - квадрат делят на четыре части, ко торые обозначают буквами, например минометная батарея (4916-Б). 14.Ориентиры, их виды.15.Виды определения расстояния по карте, показать на топографической карте.Измерения, проводимые по топографической карте
Измерения по линейному масштабу выполняют с помощью циркуля-измерителя. Для этого достаточно измерить циркулем, линейкой или полоской бумаги расстояние между заданными точками на карте, а затем приложить циркуль к линейному масштабу и снять по нему отсчет (рис. 12). 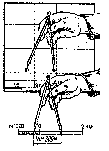 Рис. 12. Измерения по линейному масштабу с помощью циркуля-измерителя В практике очень часто приходится измерять расстояния не по прямым, а по ломаным или извилистым линиям, например, длину маршрута по дорогам. В этом случае можно воспользоваться следующими приемами: - шагом циркуля; - способом наращивания раствора циркуля; - курвиметром; - на глаз. Шагом циркуля. Устанавливают небольшой раствор циркуля, который называется шагом. Длина шага зависит от степени извилистости линии, но, как правило, не должна превышать 1 см. Одну иглу циркуля ставят в начальную точку маршрута, а вторую – в направлении измеряемой линии (рис. 13а). Поворачивая циркуль относительно одной из игл, шагают по маршруту. Общая длина маршрута АС равна числу шагов, умноженному на шаг циркуля в масштабе карты (АВ) плюс остаток ВС, измеренный по линейному масштабу.   Измеряемая кривая делится черточками на приблизительно прямолинейные отрезки. При работе циркулем сначала ставим одну ножку на начальную точку кривой и раздвигаем циркуль до тех пор, пока вторая ножка не совпадет с первой черточкой, отмеченной на линии. Далее, держа вторую ножку плотно на бумаге, поворачиваем первую ножку так, чтобы она стала на мысленном продолжении второго отрезка, т. е. отрезка между первой и второй черточками. После этого, оставляя первую ножку в этом месте, раздвигаем циркуль до совпадения второй ножки со второй черточкой и так далее до конца маршрута. Конечный раствор циркуля будет соответствовать длине кривой в масштабе карты.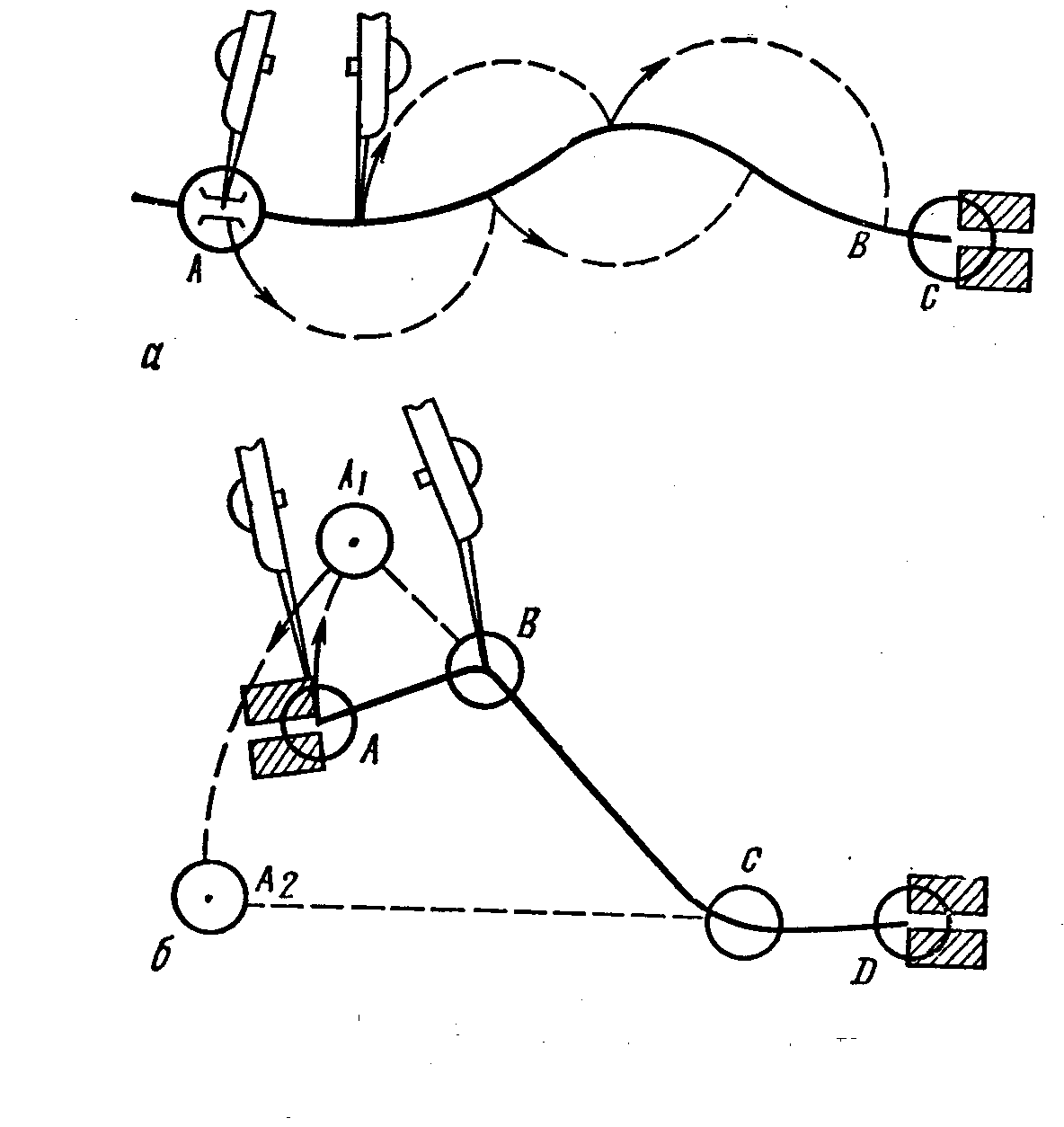 Рис. 13. Определение расстояний шагом циркуля и способом наращивания раствора циркуля Если нет циркуля, то расстояние этим способом можно определить полоской бумаги или линейкой. Край полоски прикладывают к первому участку дороги и отмечают на нем штрихами начальную точку и точку поворота. Затем полоску разворачивают так, чтобы край ее совпал со вторым участком дороги, а штрих, отмеченный на повороте – с точкой поворота. В таком положении на край полоски переносят точку второго поворота и т.д. Общее расстояние между начальным и конечным штрихами определяют по линейному масштабу. Если отрезок получился больше величины линейного масштаба, то полоску прикладывают к какой-либо линии километровой сетки, по ней подсчитывают целое число километров, а остаток определяют по линейному масштабу. Вместо полоски бумаги можно воспользоваться обычной линейкой. На нее уже не наносят штрихи, а лишь считывают число сантиметров и миллиметров по каждому участку дороги нарастающим итогом. Измеренное расстояние в сантиметрах, умноженное на величину масштаба, будет соответствовать действительному расстоянию на местности. Курвиметром. Курвиметр – прибор для измерения кривых линий. Стандартный курвиметр имеет две шкалы для измерения расстояний по карте: с одной стороны метрическую (от 0 до 100 см), с другой стороны дюймовую (от 0 до 39,4 дюйма). Механизм курвиметра состоит из обводного колеса 5, соединенного системой зубчатых передач со стрелкой 3. Для измерения длины линии на карте следует предварительно вращением обводного колеса установить стрелку курвиметра на начальное (нулевое) деление шкалы 1, а затем прокатить обводное колесо строго по измеряемой линии. Полученный отсчет по шкале курвиметра необходимо умножить на величину масштаба карты. Правильность работы курвиметра проверяют путем измерения известной длины линии, например расстояния между линиями километровой сетки на карте. Погрешность в измерении линии длиной 50 см курвиметром составляет не более 0,25 см. На глаз. При глазомерном определении расстояний по карте пользуются стороной квадрата километровой сетки как эталоном. Сравнивая расстояния отрезков со стороной квадрата, определяют число километров, а десятые доли километра оценивают на глаз. Точность измерения расстояний. Точность измерения длины прямолинейных отрезков на топографической карте с помощью циркуля-измерителя и поперечного масштаба не превышает 0,1 мм. Эта величина называется предельной графической точностью измерений, а расстояние на местности, соответствующее 0,1 мм на карте, – предельной графической точностью масштаба карты. Графическая ошибка измерения длины отрезка на карте зависит от деформации бумаги и условий измерения. Обычно она колеблется в пределах 0,5-1 мм. Поправка в расстояние за наклон линии. Измеренное по карте расстояние на местности будет всегда несколько меньше. Это происходит потому, что на карте измеряют горизонтальные проложения, в то время как соответствующие им линии на местности обычно наклонные. |