Метожическме рекомендациии по контрольной математика СИБГУТИ. Справочник по элементарной и высшей математике, прилагаемый к курсу (далее Справочник ). Работа может быть зачтена даже в случае незначительных ошибок в решении, но может быть возвращена на доработку в случае существенной ошибки
 Скачать 160.8 Kb. Скачать 160.8 Kb.
|
|
Методические указания к выполнению контрольной (экзаменационной) работы по дисциплине «Математика. Часть 2» 1. Общие указания. Перед решением контрольной работы следует полностью выписать её условие. Решения задач располагайте в порядке возрастания номеров, указанных в задании. Решения следует излагать, объясняя и мотивируя основные действия по ходу решения. Необходимые рисунки следует помещать в тексте по ходу решения. Ответы в конце решения задачи следует выделять. Желательно использование текстового редактора и редактора формул. В крайнем случае, принимаются сканы отчетливо выполненных рукописных текстов и рисунков. Контрольную, а также и экзаменационную работу, следует посылать отдельным файлом, помещая в начале титульный лист и задание. При необходимости можно использовать справочник по элементарной и высшей математике, прилагаемый к курсу (далее – Справочник). Работа может быть зачтена даже в случае незначительных ошибок в решении, но может быть возвращена на доработку в случае существенной ошибки. 2. Примеры решения задач. Задание 1. Найти неопределенные интегралы а) 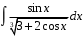 б) б) 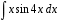 в) 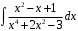 г) г) 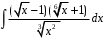 . .Решение. а). Используем замену переменной. 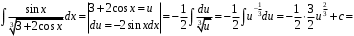 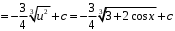 б). Используем метод интегрирования по частям (см. Справочник) 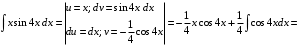 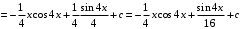 в). Подынтегральную дробь представим в виде суммы простейших дробей 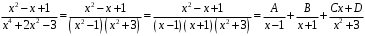 . .Неопределенные коэффициенты A,B,C,Dнайдем из условия 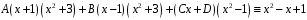 . .Раскрывая скобки и приравнивая коэффициенты при одинаковых степенях в правой и левой части этого тождества, получим систему уравнений 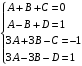 Решая эту систему, получим 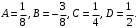 Таким образом 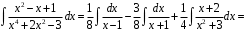 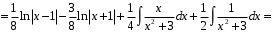 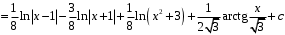 . .г). После замены 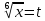 т.е. т.е. 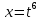 получим интеграл получим интеграл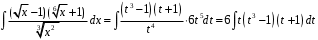 Далее решение очевидно. Задача 2. Исследовать сходимость интеграла 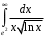 Решение: Вычисляя несобственный интеграл, внесем под знак дифференциала 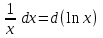 , тогда , тогда 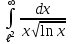 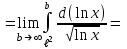 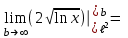 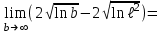 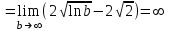 , так как функция , так как функция 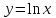 неограниченно возрастает при неограниченно возрастает при 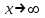 . .Следовательно, интеграл 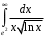 расходится. расходится.Задача 3. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Решение: Изобразим тело Т: 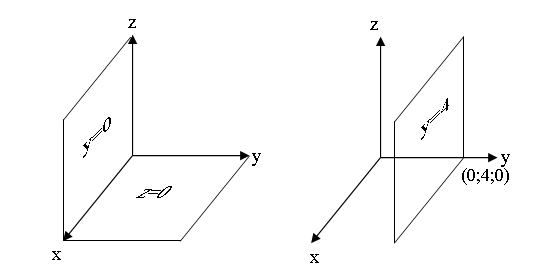 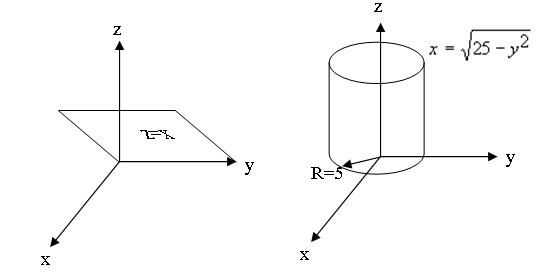 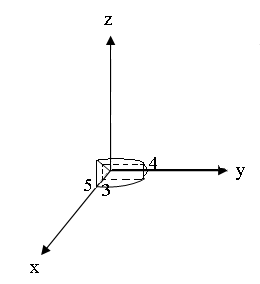  Dxy Тело Т находится над областью Dxy в плоскости z=0 и сверху накрывается плоскостью z=x. Вычислим объем Т 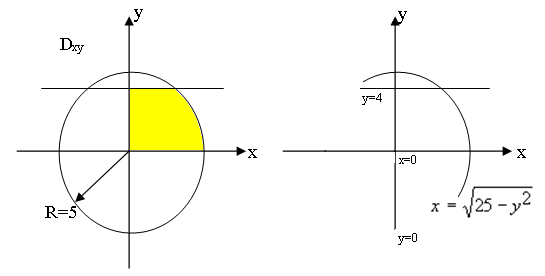 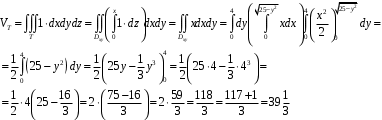 Ответ: объем тела равен 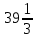 (куб.ед.) (куб.ед.)Задача 3. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями Решение: 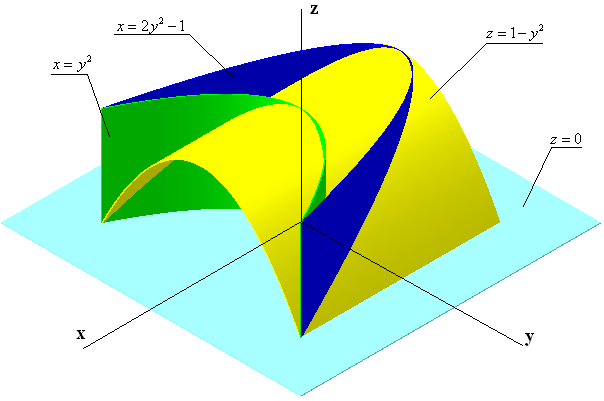 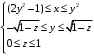 Расставим пределы интегрирования для повторного интеграла и проинтегрируем 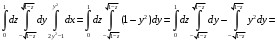 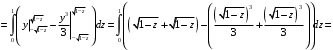 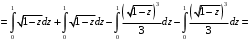 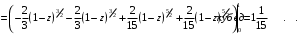 Задача 4. Изменить порядок интегрирования 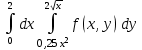 Решение. Восстановим область интегрирования, ограниченную линиями: 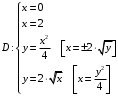 Изобразим область интегрирования: 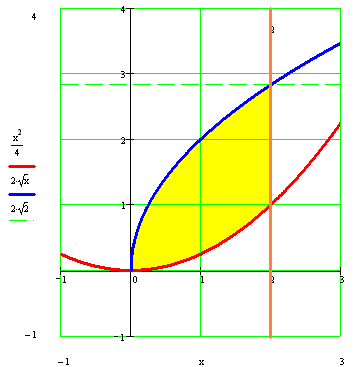 Осуществим смену координатных осей: 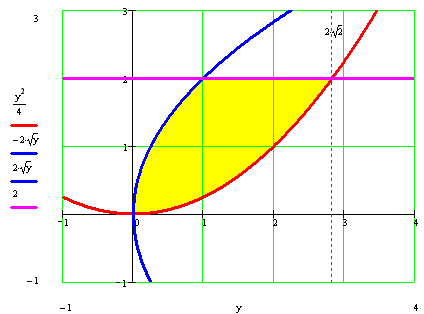 Изменим порядок интегрирования в повторном интеграле: 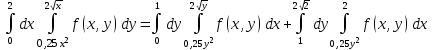 |
