Прогнозирование миграционного прироста. Спрогнозировать значение социальноэкономического показателя в соответствии с вариантом (табл. 1)
 Скачать 136.55 Kb. Скачать 136.55 Kb.
|
|
Спрогнозировать значение социально-экономического показателя в соответствии с вариантом (табл. 1). Указание. Описать содержание, способы измерения, методы расчета, экспертное мнение о тенденциях развития изучаемого показателя. Исходные данные за последние несколько лет взять на сайте Росстата www.gks.ru, либо в других доступных источниках, подтвердить достоверность данных скриншотом и ссылкой. Построить график временного ряда показателя в соответствии с вариантом. При необходимости осуществить предпрогнозную подготовку. По внешнему виду графика выбрать подходящую аппроксимирующую кривую. Рассчитать параметры кривой, среднюю абсолютную процентную ошибку модели. Сделать вывод о пригодности модели для прогнозирования. С помощью выбранной модели рассчитать прогнозируемое значение показателя на один и два года вперед, а также доверительный интервал прогноза на базе стандартной ошибки прогноза. На графике привести теоретическую кривую и показать прогнозируемое значение. Использовать адаптивные методы (выбрать метод самостоятельно на основании специфики развития), значение параметра сглаживания выбрать самостоятельно; исходный прогноз сделать на основе экспертной оценки. Оценить среднее квадратическое отклонение, нижнюю и верхнюю границы прогноза. Оценить точность прогноза с помощью абсолютной процентной ошибки, средней процентной ошибки и средней ошибки. Построить графики для фактического значения показателя, прогнозного значения, нижней и верхней границы прогноза. Выбрать наиболее точный и достоверный прогноз. Сделать выводы. Исходные данные  Миграционный прирост – это разность между теми, кто приехал в какой-либо регион и уехал оттуда. При получении отрицательного числа говорят о миграционной убыли. В России для определения миграционного прироста учитываются только лица, получившие право на постоянное место жительства (ПМЖ) или покинувшие страну с намерением получить такую возможность в другой стране. Это безвозвратный тип миграции населения. Для расчетов существует формула миграционного прироста: МП = П – В (человек), где МП означает величину миграционного прироста, П – число прибывших, В – число выбывших. В таблице 1 и рис. 2 представлена динамика миграционного прироста населения за последние 10 лет. Таблица 1 Миграционный прирост населения
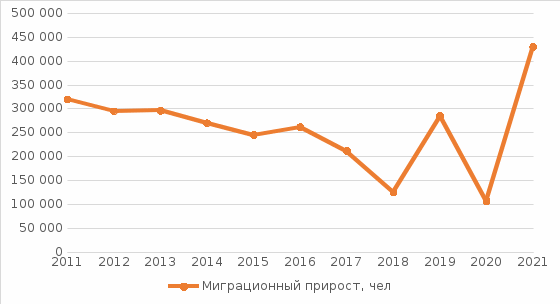 Рис. 2. Миграционный прирост населения 2011–2021 гг., чел. На основе полученной кривой миграционного прироста населения за последние 10 лет невозможно выбрать аппроксимирующую кривую только по внешнему виду графика. Построим линии тренда и выберем наиболее подходящую по значению коэффициента детерминации. 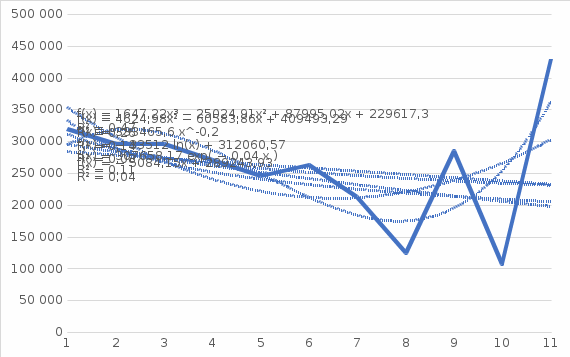 Рис. 3. Линии тренда миграционного прироста населения Как видно по графику, наиболее оптимальной из всех линий является полином 3-й степени. Уравнение регрессии: y = 1647,2x3 – 25025x2 + 87995x + 229617 Коэффициент R2 = 0,4743. Следовательно, достоверность прогноза данной аппроксимирующей кривой составляет 47,43%. Проведем необходимые расчеты оценки качества прогноза и построения верхней и нижних границ в таблице 3 при использовании MS Excel. Для этого сначала рассчитаем отклонения фактических значений показателя от прогнозных. Каждое отклонение возьмем по модулю. Для этого в ячейке E2 наберем формулу = =ABS(D2) и протянем ее до ячейки E11. Найдем Среднее, набрав в ячейке E15 формулу: = =СРЗНАЧ(E2:E12). Получаем абсолютную ошибку – 47 304 чел. Рассчитаем среднюю процентную ошибку. В ячейке F2 введем формулу: =D2/B2 и протянем ее до F12. Найдем среднюю процентную ошибку прогноза, набрав в ячейке F15 формулу: =СРЗНАЧ(F2:F12) и установим формат ячейки – процентный. Получили MPE = -10,35% - средняя процентная ошибка меньше 5%, что говорит о том, что прогноз не смещен. Оценим точность прогноза, рассчитав среднюю абсолютную процентную ошибку: В ячейке G4 введем формулу: =D2/B2 и протянем ее до G12. Найдем среднюю абсолютную процентную ошибку прогноза, набрав в ячейке G15 формулу: =СРЗНАЧ(G2:G12) и установим формат ячейки – процентный. Получили MAPE = 26,20% - это больше5%, что говорит о низкой точности прогноза. Определим верхнюю и нижнюю границы прогноза, для чего сначала рассчитаем среднее квадратическое отклонение. Для определения границ доверительного интервала используется выражение: 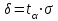 , ,где 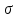 - среднеквадратическое отклонение; - среднеквадратическое отклонение;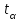 - критерий Стьюдента - критерий СтьюдентаПри вероятности равной 95% и числе степеней свободы 7-2=5 критерий Стьюдента t=2,570. Границы прогноза принимаются как 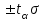 : :Получили итоговый график прогнозов. 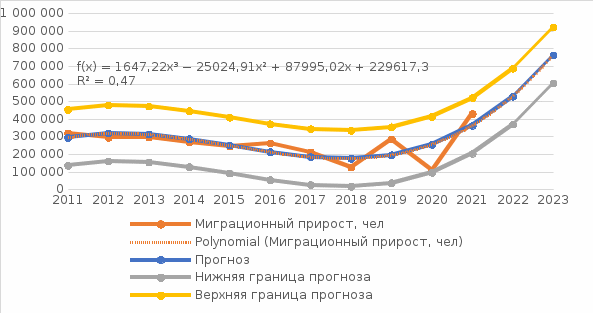 Таким образом, для данного временного ряда показателя аппроксимирующей прямой является y = 1647,2x3 – 25025x2 + 87995x + 229617 Средняя абсолютная процентная ошибка модели равна 26,20% Прогнозируемое значение показателя на один и два года вперед равны 528 319 и 763 225 человек соответственно. Доверительный интервал в эти прогнозируемые годы равен 369 388 – 687 249 и 604 295 – 922 156 соответственно. СКО = 61 841 Средняя процентная ошибка равна -10,35% Точность прогноза можно оценить как низкая. Таблица 2 Расчет верхней и нижней границы прогноза
Важным методом стохастических прогнозов является метод экспоненциального сглаживания. Этот метод заключается в том, что ряд динамики сглаживается с помощью скользящей средней, в которой веса подчиняются экспоненциальному закону. Экспоненциальная средняя вычисляется по рекуррентной формуле: St = α*Yt + (1- α)St-1 где St – значение экспоненциальной средней в момент t; St-1 – значение экспоненциальной средней в момент (t = 1); Что касается начального параметра S0, то в задачах его берут или равным значению первого уровня ряда у1, или равным средней арифметической нескольких первых членов ряда. Yt – значение экспоненциального процесса в момент t; α – вес t-ого значения ряда динамики (или параметр сглаживания). Последовательное применение формулы дает возможность вычислить экспоненциальную среднюю через значения всех уровней данного ряда динамики. Наиболее важной характеристикой в этой модели является α, по величине которой практически и осуществляется прогноз. Чем значение этого параметра ближе к 1, тем больше при прогнозе учитывается влияние последних уровней ряда динамики. Если α близко к 0, то веса, по которым взвешиваются уровни ряда динамики убывают медленно, т.е. при прогнозе учитываются все прошлые уровни ряда. В специальной литературе отмечается, что обычно на практике значение α находится в пределах от 0,1 до 0,3. Значение 0,5 почти никогда не превышается. Экспоненциальное сглаживание применимо, прежде всего, при постоянном объеме потребления (α = 0,1 – 0,3). При более высоких значениях (0,3 – 0,5) метод подходит при изменении структуры потребления, например, с учетом сезонных колебаний. Найдем параметр α по следующей формуле: α = 2/(11+1) = 0.17 В качестве S0 берем среднее арифметическое первых 3 значений ряда. S0 = (319761 + 294930 + 295859)/3 = 303516.67
Базовое уравнение имеет следующий вид: S(t+1) = S(t)(1 - α) + αY(t) S(t) – это прогноз, сделанный в момент времени t; S(t+1) отражает прогноз во временной период, следующий непосредственно за моментом времени t. S(11+1) = 379373.827(1 - 0.17) + 0.17 * 429902 = 387963.616 Стандартная ошибка (погрешность) рассчитывается по формуле: 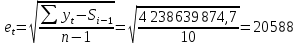 Найдем верхнюю и нижнюю границу прогноза аналогично аппроксимирующей кривой. Сравним данные скользящей средней и экспоненциального сглаживания на основе рис. 4 и рис. 5, табл. 4 и табл. 5. Наиболее точным является прогноз, произведенный на основе экспоненциального сглаживания, т.к. средняя абсолютная процентная ошибка модели равна 5,85% против 23,4% на основе прогноза по скользящей средней. 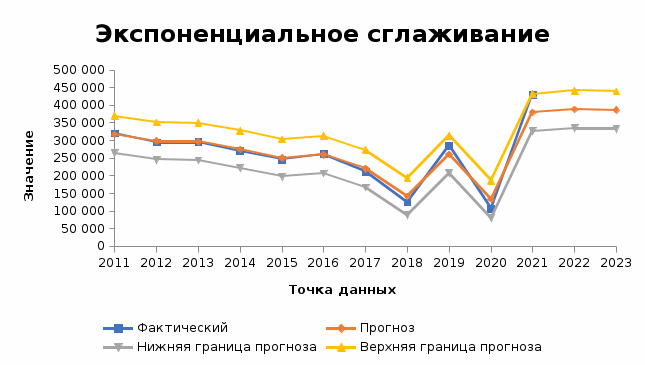 Рис. 4. Прогноз на основе экспоненциального сглаживания 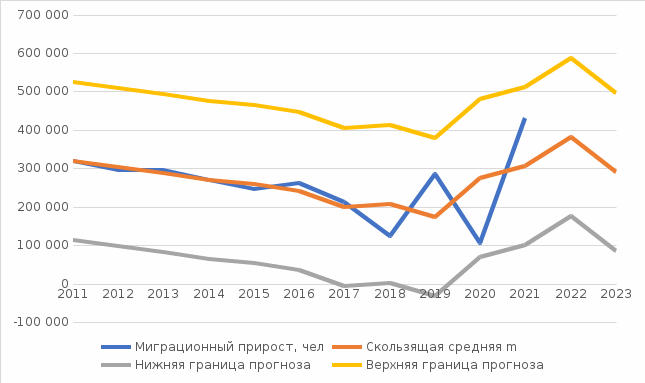 Рис. 5. Прогноз на основе скользящей средней Таблица 4 Прогнозирование на основе скользящей средней
Таблица 5 Прогнозирование на основе экспоненциального сглаживания
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
