Средние величины
 Скачать 20.78 Kb. Скачать 20.78 Kb.
|
|
СРЕДНИЕ ВЕЛИЧИНЫ Вариационные ряды и их графики дают наглядное представление о варьировании признаков, но они недостаточны для полного описания варьирующих объектов. Для этой цели служат особые, логически и теоретически обоснованные числовые показатели, называемые статистическими характеристиками. К ним относятся, прежде всего, средние величины и показатели вариации. В отличие от индивидуальных числовых характеристик средние величины обладают устойчивостью, способностью характеризовать целую группу однородных единиц одним (средним) числом. И хотя средние величины абстрактны, они вполне вероятны и ощутимы. Средний рост, средняя продуктивность, средний урожай, средняя успеваемость и другие средние – все это понятия абстрактные о конкретном. Значение средних заключается в их свойстве аккумулировать или уравновешивать все индивидуальные отклонения, в результате чего проявляется то наиболее устойчивое и типичное, что характеризует качественное своеобразие варьирующего объекта, позволяет отличать один групповой объект от другого. В зависимости от того, как распределены первичные данные - в равно- или в неравноинтервальный вариационный ряд, - для их характеристики применяют разные средние величины. Именно при распределении собранных данных в неравноинтервальный вариационныйряд более подходящий обобщающей характеристикой изучаемого объекта служит так называемая плотность распределения, т.е. отношение частот или относительных частот к ширине кассовых интервалов, как это показано в табл. 1. Таблица 1 здесь должна быть таблица Кроме того, числовыми характеристиками таких рядов могут служить средние из абсолютных или относительных показателей плотности распределения. Средняя плотность показывает, сколько единиц данной совокупности приходится на интервал, равный единице измерения учитываемого признака. Так, по табл. 1 находим, что средние из относительных (процентных) показателей плотности распределения голубей в стае в гнездовой период 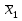 и в остальное время года и в остальное время года 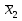 оказывается следующими: оказывается следующими: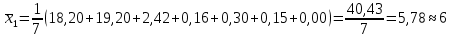 и 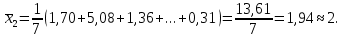 Таким образом, выясняется, что в среднем относительная плотность числености голубей в стае в гнездовой период в три раза выше, чем в остальное время года. В качестве статистических характеристик равноинтервальных вариационных рядов применяют степенные и структурные (нестепенные) средние величины. Степенные величины вычисляют, исходя из общей формулы 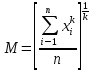 или или 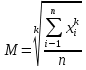 где 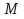 – средняя величина; – средняя величина; 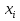 – варианта; – варианта; 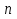 – число наблюдений, для которых вычисляют среднюю; – число наблюдений, для которых вычисляют среднюю; 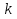 – величина, по которой определяют вид средней. Так, при – величина, по которой определяют вид средней. Так, при 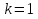 получается средняя арифметическая, при получается средняя арифметическая, при 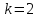 – средняя квадратическая, при – средняя квадратическая, при 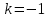 образуется средняя гармоническая и т.д. Из структурных средних в биологии применяю медиану, моду и др. образуется средняя гармоническая и т.д. Из структурных средних в биологии применяю медиану, моду и др.Средние величины могут характеризовать только однородную совокупность вариант. Если средняя получена на качественно неоднородном материале или выбрана неправильно, без учета специфики характеризуемого явления или процесса, она окажется фиктивной. При наличии разнородных по составу данных их необходимо группировать в отдельные группы и вычислить групповые или частные средние. Средние величины принято обозначать теми же строчными буквами латинского алфавита, что и варианты, с той лишь разницей, что над буквой, соответствующей средней величине, ставя черту. Так, если признак обозначен через 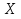 , то его числовые значения выражают буквой , то его числовые значения выражают буквой 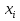 , среднюю арифметическую - , среднюю арифметическую - 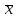 , среднюю гармоническую - , среднюю гармоническую - 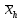 и т.д. При вычислении средних величин и других статистических характеристик не обязательно распределять исходные данные в вариационный ряд. и т.д. При вычислении средних величин и других статистических характеристик не обязательно распределять исходные данные в вариационный ряд. Наиболее подходящим оказался показатель, построенный не на отклонениях вариант от их средних, а на квадратах этих отклонений. Этот показатель называется дисперсией (от лат. dispersio - рассеяние) и выражают формулой 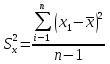 (1) (1)или при повторяемости отдельных вариант 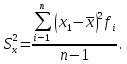 (2) Следует также иметь в виду, что вместо 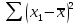 можно использовать выражения можно использовать выражения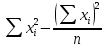 , , 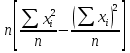 , , 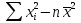 . .Отсюда можно вывести следующие рабочие формулы, удобные при вычислении дисперсии непосредственно по значениям варьирующего признака: 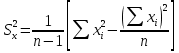 или или 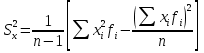 , (3) , (3)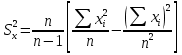 или или 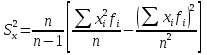 , (4) , (4)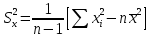 или или 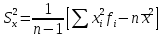 .(5) .(5)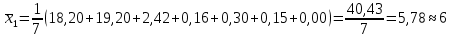 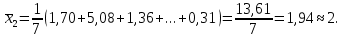 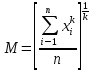 или или 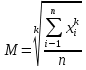 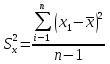 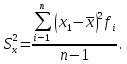 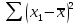 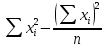 , , 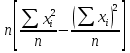 , , 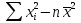 . .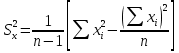 или или 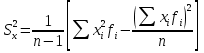 , ,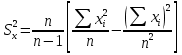 или или 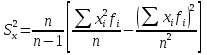 , ,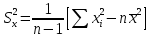 или или 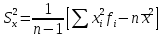 . . |
